3.3.2.Угловая скорость

Если за промежуток
времени

тело совершит поворот на угол

,
то средняя угловая скорость тела
за этот промежуток времени равна:

.

Угловая скорость
в данный момент времени называется
величина, к которой стремится средняя
угловая скорость ω_ср,
когда промежуток времени Δt→0.

, или

.
(3.5)

Таким образом,
угловая скорость в данный
момент времени численно равна первой
производной от угла поворота по времени.
Знак определяется направлением вращения
тела. Легко видеть, что когда вращение
происходит против хода часовой стрелки
ω>0, а когда по ходу часовой стрелки,
ω<0. Размерность угловой скорости

= с^-1, так как радиан – величина
безразмерная.

Условимся угловую
скорость изображать в виде вектора

,
численная величина которого равна
и который направлен вдоль оси вращения
тела в ту сторону, откуда вращение видно
происходящим против хода часовой
стрелки. Такой вектор определяет сразу
модуль угловой скорости, ось вращения
и направление вращения тела вокруг оси.

3.3.3. Угловое ускорение

Угловое ускорение
характеризует изменение угловой скорости
с течением времени. Если за промежуток
угловая скорость изменилась на

,
то среднее угловое ускорение
тела за этот промежуток времени будет
численно равно
.

Угловым ускорением
в данный момент времени называется
величина, к которой стремится значение

,
когда промежуток времени Δt→0,
следовательно:

,
или

.
(3.6)

Итак, угловое
ускорение тела в данный момент
времени численно равно первой
производной от угловой скорости или
второй производной от угла поворота
тела.

Размерность
углового ускорения [ε]=1/c²
=с^-2

Если
модуль угловой скорости с течением
времени возрастает, то движение
называется ускоренным, если
убывает – то замедленным.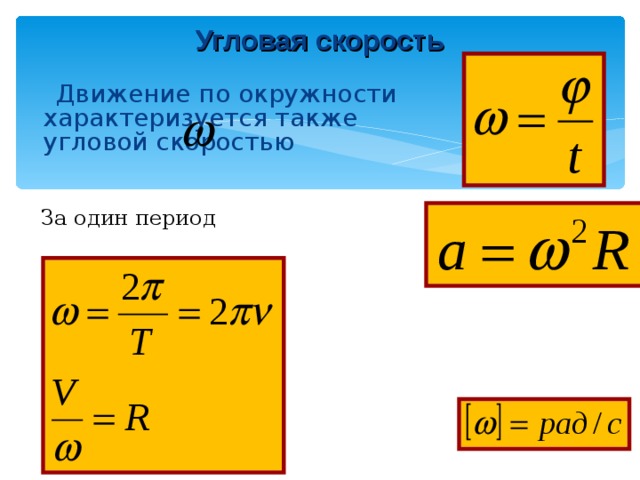 Легко
видеть, что вращение будет ускоренным,
если ω и ε имеют одинаковые
знаки, и замедленным, если ω и ε
имеют разные знаки.

Угловое ускорение
тела (по аналогии с угловой скоростью)
можно изобразить вектором

,
направленным вдоль оси вращения. При
этом направление
совпадает с направлением
,
если движение ускоренное (рис. 3.4) и
противоположно направлению
,
если движение замедленное (рис. 3.5)

Pис.
3.4 Рис. 3.5

Ускоренное
вращение Замедленное вращение

3.3.4. Равномерное и равнопеременное вращение

Вращение тела с
постоянной угловой скоростью ω =
const называется
равномерным.

Найдем закон
равномерного вращения. При условии, что
при t = 0, φ = φ_0.
Из (3.5) имеем

.
Проинтегрировав это уравнение в пределах
слева от φ до φ₀, справа от
0 до t, получим:

,
oткуда

.
(3.7)

Выражение (3.7)
является уравнением равномерного
вращения тела.

Из уравнения (3.7)
находим

,
то есть угловая скорость равномерного
вращения тела равна отношению
приращения угла поворота за некоторый
промежуток времени к величине этого
промежутка времени.

В технике угловая
скорость измеряется числом оборотов в
минуту и обозначается n. Так как,
один оборот равен 2π рад, то
зависимость между угловой скоростью
[n] = об/мин и [ω] = с^—1
при φ₀ = 0 имеет вид

.
(3.8)

Пример
1.
Определить
угловую скорость Земли вокруг ее оси,
выраженной в с^—1.

Решение:

.

Вращение тела
при котором угловое ускорение постоянно
(ε=const) во все
время движения, называется равнопеременным.

Найдем закон
равнопеременного вращения, если при
t=0, φ=φ₀, ω=ω₀.
Из (3.6) имеем:

.
Это уравнение проинтегрируем в пределах,
соответствующих начальному моменту
t₀ и произвольному
моменту времени t. Получим

,
или

.
(3.9)

Подставим
полученное выражение в уравнение
,
тогда

.
Интегрируя его в соответствующих
пределах, получим:
,
или

(3.10)

Пример
2.
Вал начитает вращаться из состояния
покоя. В первые 10 с
он совершает
200 оборотов. Каковы его угловые скорость
и ускорение по истечении 20 с?

Решение.
Так как вал начинает вращаться из
состояния покоя, то

.
В этом случае уравнения (3.9) и (3.10) при

=
0 имеют вид

,
(а)

.
(б)

Из
уравнения (б) находим

,
где φ
= 2π
N.
Подставляя числовые значения, находим:

с^—2,

с^—1.

Вращающий момент через угловую скорость

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

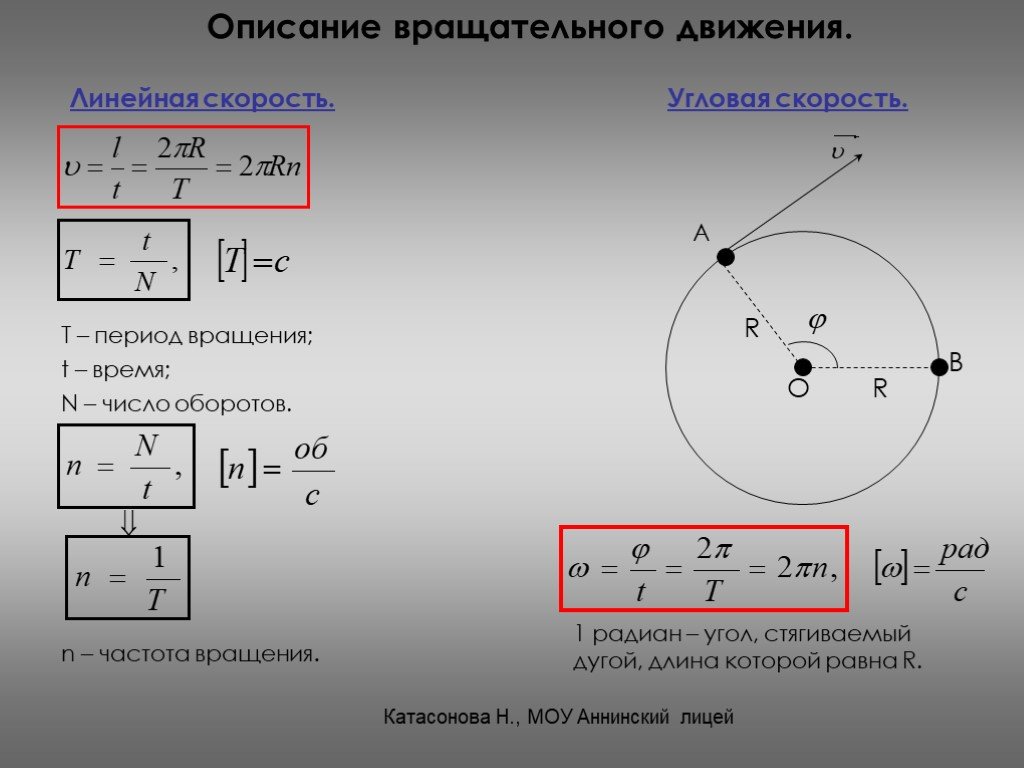
За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с 2 .

Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ _{+ ωt,} где φ _{– начальное значение угла поворота.}

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω_{+ εt,} φ = φ _{+ ωt + εt 2 /2.}

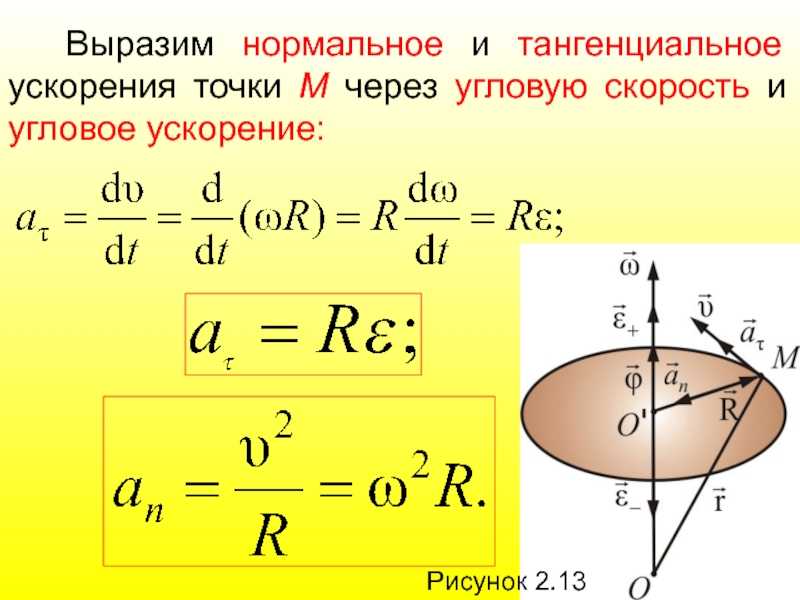
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц = v 2 /R = (ωR) 2 /R = ω 2 R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R 2 mβ, β= M/mR 2 = M/I, где I = mR 2 — момент инерции материальной точки.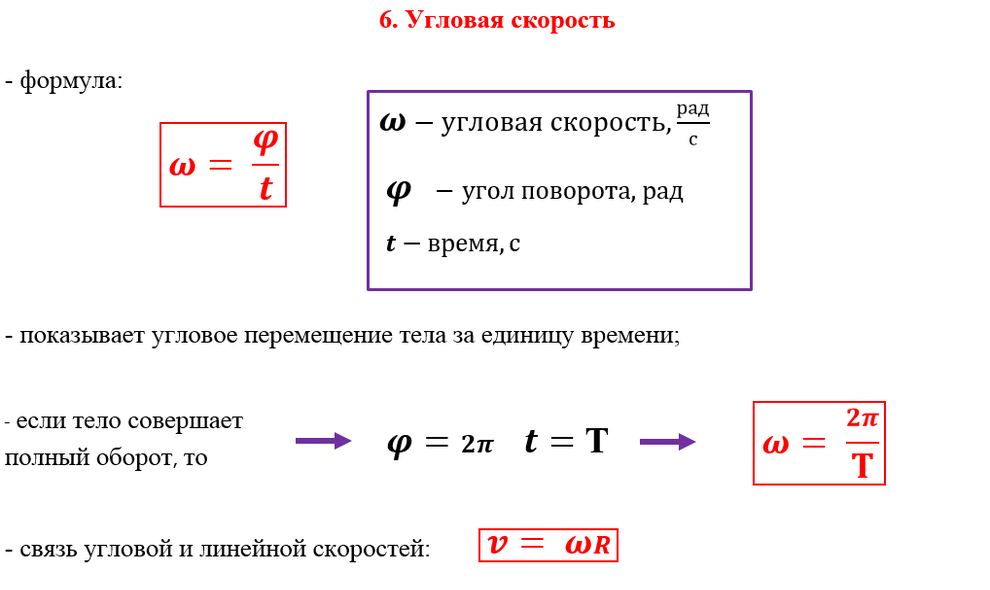 Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω _{— εt.}

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω_{/t = 2πn/t.}

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ _{+ ωt + εt 2 /2. У}читывая выражение для углового ускорения и то, что φ _{= 0}, находим: φ(t)= ω_{t/2 = πnt.}

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).

Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.

Найдем время, за которое диск остановится: t = ω_/ε, где ω — начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.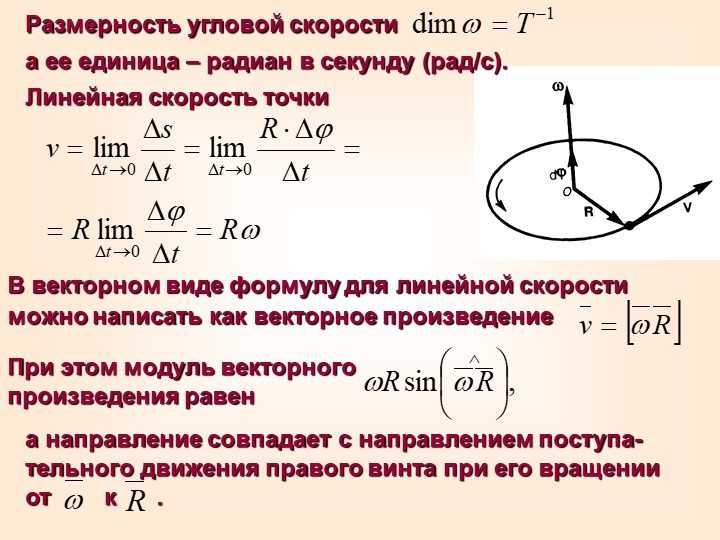

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с 2 .

Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ _{+ ωt,} где φ _{– начальное значение угла поворота.}

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω_{+ εt,} φ = φ _{+ ωt + εt 2 /2.}

Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц = v 2 /R = (ωR) 2 /R = ω 2 R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R 2 mβ, β= M/mR 2 = M/I, где I = mR 2 — момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω _{— εt.}

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω_{/t = 2πn/t.}

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ _{+ ωt + εt 2 /2. У}читывая выражение для углового ускорения и то, что φ _{= 0}, находим: φ(t)= ω_{t/2 = πnt.}

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).

Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.

Найдем время, за которое диск остановится: t = ω_/ε, где ω — начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

Движение твердого тела, при котором все его точки перемещаются по окружности, центры которой расположены на перпендикулярной этим окружностям неподвижной прямой, называется вращательным. Неподвижная прямая, на которой лежат центры круговых траекторий то­чек тела, называется его осью вращения. Для образования оси вра­щения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел можно привести движение две­рей или створок окон при их открывании или закрывании.

Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).

Рис. 7.3. К анализу вращательного движения твердого тела

Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя.

Для установления закона вращательного движения тела, по кото­рому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную полуплоскость НП, а внутри тела отметим подвижную полуплоскость, ко­торая вращается около оси вместе с телом, теперь угол φ, образуемый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, т. е. знать закон вращательного движения тела:

Быстрота изменения угла поворота во времени характеризуется величиной, которая называется угловой скоростью.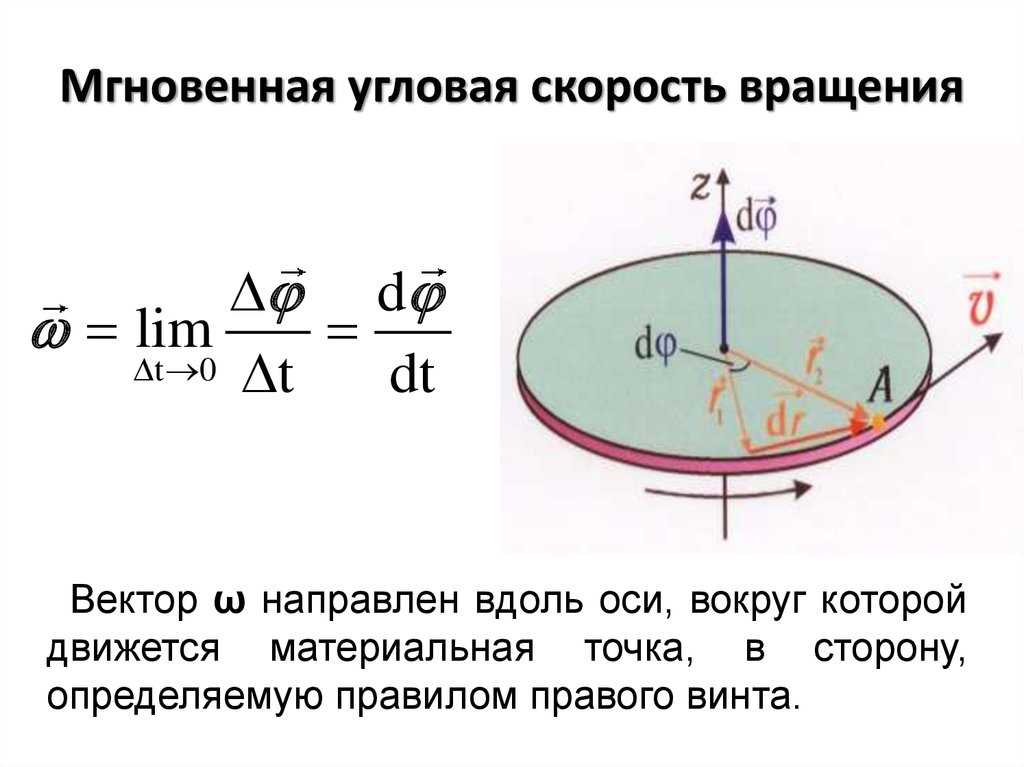

Представим, что в некоторый момент времени t положение вращающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело повернулось на угол Δ φ, и величина

называется средней угловой скоростью.

Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение, обозначаемое . Среднее ускорение ;

.

Единица углового ускорения 1 рад/с 2 .

Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часовой стрелки – отрицательным.

Рис. 7.4. К определению вида вращательного движения

Векторы и – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора (или ), видеть вращение, происходящее против часовой стрелки.

Если векторы и направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы и направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).

7.3. Частные случаи вращательного движения

1. Равномерное вращательное движение. Если угловое ускорение и, следовательно, угловая скорость

, (7.1)

то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных получим

Если при изменении времени от 0 до t угол поворота изменялся от φ _{(начальный угол поворота) до φ, то, интегрируя уравнение в этих пределах:}

получаем уравнение равномерного вращательного движения

,

которое в окончательном виде записывается так:

.

Если , то

.

Таким образом, при равномерном вращательном движении угловая скорость

или при .

2. Равнопеременное вращательное движение. Если угловое ускорение

(7.2)

то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.2):

и приняв, что при изменении времени от 0 до t угловая скорость изменилась от (начальная угловая скорость) до , проинтегрируем уравнение в этих пределах:

или ,

т. е. получим уравнение

(7.3)

выражающее значение угловой скорости в любой момент времени.

Закон равнопеременного вращательного движения или, с учетом уравнения (7.3):

Полагая, что в течение времени от 0 до t угол поворота изменялся от до, проинтегрируем уравнение в этих пределах:

или

Уравнение равнопеременного вращательного движения в оконча­тельном виде

(7.4)

Первую вспомогательную формулу получим, исключив из формул (7.3) и (7.4) время:

(7.5)

Исключив из тех же формул угловое ускорение , получим вторую вспомогательную формулу:

(7.6)

где – средняя угловая скорость при равнопере­менном вращательном движении.

Когда и , формулы (7.3)–(7.6) приобретают более простой вид:

В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.

Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между (с –1 ) и n (мин –1 ). Так как , то при n (мин –1 ) за t = 1 мин = 60 с угол поворота . Следовательно:

.

При переходе от угловой скорости (с –1 ) к частоте вращения n (мин –1 ) имеем

Угловая скорость | Medical Journals

В физике угловая скорость означает, насколько быстро объект вращается или вращается относительно другой точки, т. е. насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и спиновая угловая скорость. Угловая скорость вращения относится к тому, насколько быстро твердое тело вращается относительно своего центра вращения. Орбитальная угловая скорость относится к тому, как быстро точечный объект вращается вокруг фиксированного начала координат, то есть к скорости изменения его углового положения относительно начала координат. Угловая скорость вращения не зависит от выбора начала координат, в отличие от орбитальной угловой скорости, которая зависит от выбора начала координат.

Как правило, угловая скорость измеряется в углах в единицу времени, т.е. радиан в секунду (угол заменяет расстояние от линейной скорости общим временем). Единица угловой скорости в системе СИ выражается в радианах в секунду, при этом радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ указаны как 1/с или с-1. Угловая скорость обычно обозначается символом омега (ω, иногда Ω). По соглашению, положительная угловая скорость указывает на вращение против часовой стрелки, а отрицательная — по часовой стрелке.

Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = (360°)/(24 ч) = 15°/ч, или (2π рад) /(24 ч) ≈ 0,26 рад/ч.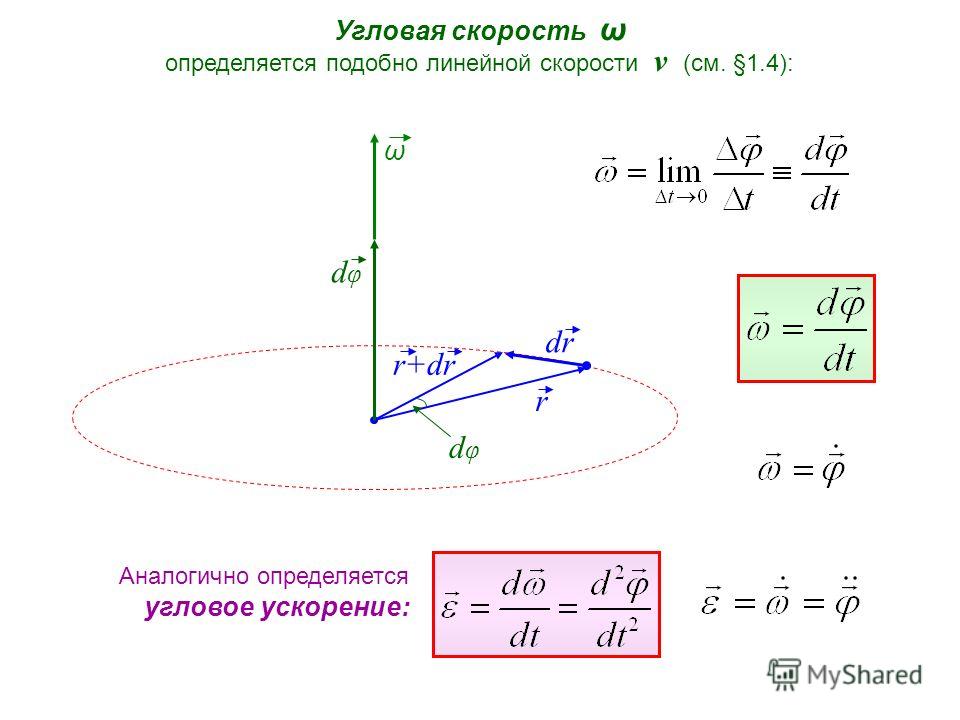 Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega {\ displaystyle v = r \ omega}. Таким образом, при радиусе орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 км × 0,26 / ч ≈ 11 000 км / ч. Угловая скорость положительна, поскольку спутник движется на восток с вращением Земли (против часовой стрелки от северного полюса). В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, и его направление указывает перпендикуляр к мгновенной плоскости вращения или углового смещения. Ориентация угловой скорости условно задается правилом правой руки.

В физике угловая скорость означает, насколько быстро объект вращается или вращается относительно другой точки, т. е. насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и спиновая угловая скорость. Угловая скорость вращения относится к тому, насколько быстро твердое тело вращается относительно своего центра вращения. Орбитальная угловая скорость относится к тому, как быстро точечный объект вращается вокруг фиксированного начала координат, то есть к скорости изменения его углового положения относительно начала координат. Угловая скорость вращения не зависит от выбора начала координат, в отличие от орбитальной угловой скорости, которая зависит от выбора начала координат.

Как правило, угловая скорость измеряется в углах в единицу времени, т.е. радиан в секунду (угол заменяет расстояние от линейной скорости общим временем). Единица угловой скорости в системе СИ выражается в радианах в секунду, при этом радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ указаны как 1/с или с-1. Угловая скорость обычно обозначается символом омега (ω, иногда Ω). По соглашению, положительная угловая скорость указывает на вращение против часовой стрелки, а отрицательная — по часовой стрелке.

Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = (360°)/(24 ч) = 15°/ч, или (2π рад) /(24 ч) ≈ 0,26 рад/ч. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega {\ displaystyle v = r \ omega}. Таким образом, при радиусе орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 км × 0,26 / ч ≈ 11 000 км / ч. Угловая скорость положительна, поскольку спутник движется на восток с вращением Земли (против часовой стрелки от северного полюса). В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, и его направление указывает перпендикуляр к мгновенной плоскости вращения или углового смещения. Ориентация угловой скорости условно задается правилом правой руки.

Соответствующие темы общей науки

Угловая скорость: значение, формула и примеры

Вы слышали о скорости и слышали об углах, но слышали ли вы об угловой скорости? Угловая скорость описывает, насколько быстро объект движется с точки зрения углов, а не с точки зрения расстояний. Это другой взгляд на движение объектов, но в некоторых случаях он может быть очень удобным, и с помощью некоторых простых формул мы действительно можем связать «нормальную» скорость с угловой скоростью. Давайте погрузимся!

Определение угловой скорости

Подобно тому, как мы сначала узнаем о положении и смещении, прежде чем узнать о скорости, мы должны сначала определить угловое положение, чтобы говорить об угловой скорости.

Угловое положение

Угловое положение объекта относительно точки и опорной линии представляет собой угол между этой опорной линией и линией, проходящей через точку и объект.

Это не самое интуитивно понятное определение, поэтому см. иллюстрацию ниже, чтобы получить четкое представление о том, что имеется в виду.

Угол a представляет собой угловое положение объекта O относительно точки P и синей контрольной линии StudySmarter Originals.

Мы видим, что абсолютные расстояния не имеют значения для углового положения, а только отношения расстояний: мы можем изменить масштаб всей этой картины, и угловое положение объекта не изменится.

Если кто-то идет прямо к вам, его угловое положение по отношению к вам не меняется (независимо от выбранной вами опорной линии).

Последний пример уже намекает на изменение угловых положений. А именно, нам не нужна конкретная опорная линия, если мы говорим только об изменении углового положения, точно так же, как нам не нужна конкретная опорная точка, если мы говорим только об изменении энергии. Изменения углового положения всегда занимают определенное время, поэтому можно говорить о скорости изменения углового положения.

Угловая скорость

Угловая скорость объекта относительно точки является мерой того, насколько быстро этот объект перемещается в поле зрения точки, в том смысле, насколько быстро изменяется угловое положение объекта.

Угловая скорость объекта по отношению к вам соответствует тому, насколько быстро вы должны поворачивать голову, чтобы смотреть прямо на объект.

Обратите внимание, что в этом определении угловой скорости нет упоминания об опорной линии, потому что она нам не нужна.

Демонстрация угловой скорости смайлика относительно его центра, адаптировано из изображения Sbyrnes321 Public domain.

Единицы угловой скорости

Из определения видно, что угловая скорость измеряется в угле в единицу времени. Поскольку углы безразмерны, единицы угловой скорости обратны единицам времени. Таким образом, стандартной единицей измерения угловой скорости является . Поскольку угол всегда имеет безразмерную меру, т.е. градусов или радианов, угловая скорость может быть записана следующими способами:

.

Здесь у нас есть знакомое преобразование между градусами и радианами как, или.

Помните, что градусы могут быть интуитивно понятны, и использовать градусы для выражения углов нормально, но в расчетах (например, при расчете угловых скоростей) всегда следует использовать радианы.

Формула угловой скорости

Давайте рассмотрим несложную ситуацию, предположим, что частица движется вокруг нас по кругу. Этот круг имеет радиус (расстояние от нас до частицы), а частица имеет скорость. Очевидно, что угловое положение этой частицы изменяется со временем из-за ее круговой скорости, и теперь угловая скорость равна

.

Очень важно использовать радианы в единицах угловой скорости при работе с уравнениями. Если вам дана угловая скорость, выраженная в градусах в единицу времени, самое первое, что вы должны сделать, это преобразовать ее в радианы в единицу времени!

Пришло время проверить, имеет ли смысл это уравнение. Во-первых, угловая скорость удваивается, если удваивается скорость частицы, что и ожидалось. Однако угловая скорость также удваивается, если радиус частицы уменьшается вдвое. Это верно, потому что частице нужно будет преодолеть только половину первоначального расстояния, чтобы совершить один полный оборот своей траектории, поэтому ей также потребуется только половина времени (поскольку мы предполагаем постоянную скорость при уменьшении вдвое радиуса).

Ваше поле зрения находится под определенным углом (грубо говоря, или), поэтому угловая скорость объекта полностью определяет, насколько быстро он перемещается в вашем поле зрения. Появление радиуса в формуле угловой скорости является причиной того, что далекие объекты движутся через ваше поле зрения гораздо медленнее, чем близкие.

Преобразование угловой скорости в линейную скорость

Используя приведенную выше формулу, мы также можем рассчитать линейную скорость объекта по его угловой скорости и радиусу следующим образом:

.

Эта формула для линейной скорости — просто манипуляция с предыдущей формулой, так что мы уже знаем, что эта формула логична. Опять же, убедитесь, что в расчетах используются радианы, а также при использовании этой формулы.

В целом можно утверждать, что линейная скорость объекта напрямую связана с его угловой скоростью через радиус круговой траектории, по которой он следует.

Угловая скорость Земли

Вращение Земли вокруг своей оси, ускоренное, Wikimedia Commons CC BY-SA 3.0.

Хорошим примером угловой скорости является сама Земля. Мы знаем, что Земля совершает полный оборот каждые 24 часа, поэтому угловая скорость объекта на экваторе Земли относительно центра Земли равна

.

Обратите внимание, как мы сразу же перевели в радианы для нашего расчета.

Радиус Земли равен, поэтому теперь мы можем рассчитать линейную скорость объекта на экваторе Земли, используя формулу, которую мы ввели ранее:

.

Угловая скорость автомобилей на кольцевой развязке

Предположим, кольцевая развязка в Далласе представляет собой идеальный круг с центром в центре города и радиусом , а ограничение скорости на этой развязке составляет . Угловая скорость автомобиля, движущегося по этой дороге на предельной скорости относительно центра города, рассчитывается следующим образом:

.

Если мы хотим, мы можем преобразовать это в градусы:

.

Угловая скорость — основные выводы

• Угловая скорость объекта относительно точки — это мера того, насколько быстро этот объект перемещается в поле зрения точки, в том смысле, насколько быстро изменяется угловое положение объекта.
• Единицами угловой скорости являются обратно пропорциональные единицы времени.