Содержание
Центрифугирование: как определить ускорение (число g) в зависимости от скорости вращения и диаметра ротора
Центрифугирование – способ разделения неоднородных, дисперсных жидких систем на фракции по плотности под действием центробежных сил. Центрифугирование осуществляют в центрифугах, принцип работы которых основан на создании центробежной силы, увеличивающей скорость разделения компонентов смеси по сравнению со скоростью их разделения только под влиянием силы тяжести. Разделение веществ с помощью центрифугирования основано на разном поведении частиц в центробежном поле. В центробежном поле частицы, имеющие разную плотность, форму или размеры, осаждаются с разной скоростью.
Скорость осаждения, или седиментации, зависит от центробежного ускорения (g), прямо пропорционального угловой скорости ротора (w, рад/с) и расстоянию между частицей и осью вращения (r, см): g = v2x r. Поскольку один оборот ротора составляет 2π радиан, то угловую скорость можно записать так: v = p x n/60, где n – скорость в оборотах в минуту, π — константа, выражающая отношение длины окружности к длине её диаметра. Угловая скорость – характеристика скорости вращения тела, измеряется обычно в радианах в секунду, полный оборот (360°) составляет 2π радиан.
Поскольку один оборот ротора составляет 2π радиан, то угловую скорость можно записать так: v = p x n/60, где n – скорость в оборотах в минуту, π — константа, выражающая отношение длины окружности к длине её диаметра. Угловая скорость – характеристика скорости вращения тела, измеряется обычно в радианах в секунду, полный оборот (360°) составляет 2π радиан.
Центробежное ускорение тогда будет равно: g =p2x r x n2/900.
Центробежное ускорение обычно выражается в единицах g (ускорение свободного падения, равное 980 м/с2) и называется относительным центробежным ускорением (ОЦУ), т.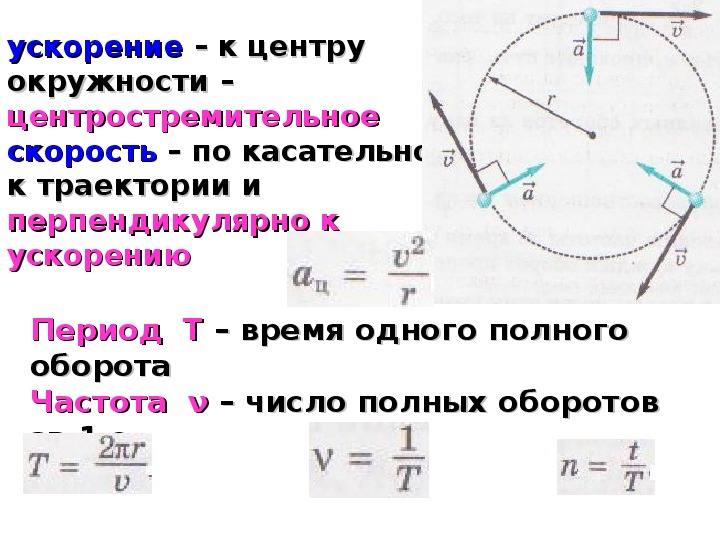 е. ОЦУ=g/980 или ОЦУ = 1,11 x 10-5 x r x n2 .
е. ОЦУ=g/980 или ОЦУ = 1,11 x 10-5 x r x n2 .
Относительное ускорение центрифуги (rcf) задается, как кратное от ускорения свободного падения (g). Оно является безразмерной величиной и служит для сравнения производительности разделения и осаждения. Относительное ускорение центрифуги (rcf) зависит от частоты вращения и радиуса центрифугирования.
Существует номограмма, выражающая зависимость относительного ускорения центрифуги (rcf) от скорости вращения ротора (n) и радиуса (r) – среднего радиуса вращения столбика жидкости в центрифужной пробирке (т.е. расстояния от оси вращения до середины столбика жидкости). Радиус измеряется (см) от оси вращения ротора до середины столбика жидкости в пробирке, когда держатель находится в положении центрифугирования.
Номограмма для определения относительного ускорения центрифуги (rcf) в зависимости от скорости вращения и диаметра ротора
r – радиус ротора, см
n – скорость вращения ротора, оборотов в минуту
rcf (relative centrifuge force) – относительное ускорение центрифуги
Радиус центрифугирования rmax– это расстояние от оси вращения ротора до дна гнезда ротора.
Для определения ускорения с помощью линейки совмещаем значения радиуса и числа оборотов на и на шкале rcf определяем его величину.
Пример: на шкале А отмечаем значение rрадиуса для ротора – 7,2 см, на шкале С отмечаем значение скорости ротора –14,000 об/мин, соединяем эти две точки. Точка пересечения образованного отрезка со шкалой В показывает значение ускорения для данного ротора. В данном случае ускорение равно 15’000.
Урок физики «Угловая и линейная скорости вращения. Решение задач»
Государственное автономное образовательное учреждение
среднего профессионального образования
Новосибирской области
«Барабинский медицинский колледж»
Цикловая методическая комиссия общих гуманитарных,
социально-экономических дисциплин
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
комбинированного занятия
для преподавателя
Дисциплина: Физика
Раздел 1 «Механика.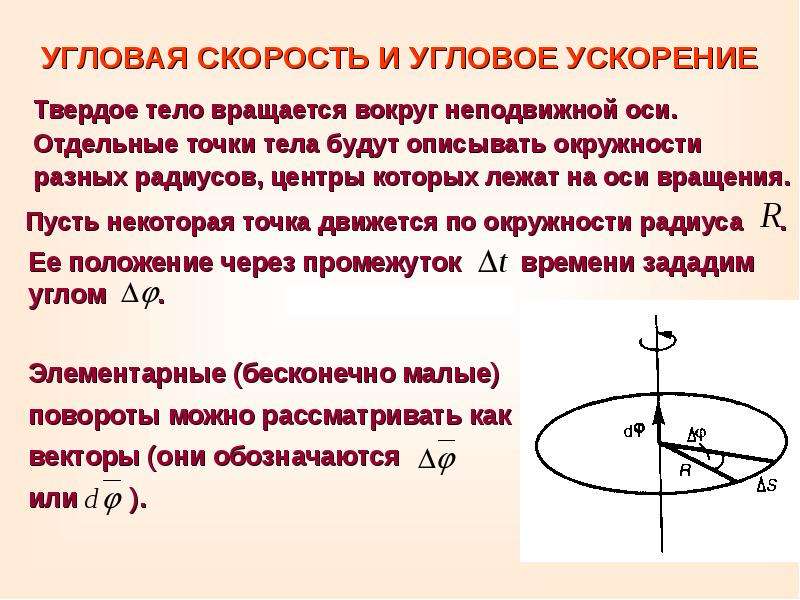 Основы динамики»
Основы динамики»
Тема 1.6 Угловая и линейная скорости вращения. Решение задач.
для специальности: «Сестринское дело»
по программе базовой подготовки
курс 1
Барабинск, 2014 г
Рассмотрена на заседании
ЦМК ОГСЭД
Протокол № ___________
От ____________ 20___г.
Председатель ЦМК
______________________
(Ф. И. О.)
______________________
(подпись)
Разработчик: преподаватель физики 1 квалификационной категории
Вашурина Т. В.
Содержание
Методический лист ………………………………………………………4
Формирование требований ФГОС при изучении темы ………………5
Выписка из тематического плана дисциплины «Физика» …………….6
Актуальность изучения темы ……………………………………………7
Примерная хронокарта занятия ………………………………………. ..8
..8
Блок информации по теме ………………………………………………11
План самостоятельной работы студентов ……………………………..15
Приложение №1 …………………………………………………………16
Приложение №2 …………………………………………………………17
Приложение №3 …………………………………………………………18
Приложение №4 …………………………………………………………18
Домашнее задание ……………………………………………………….19
Перечень оборудования и оснащения …………………………………19
Перечень литературы ……………………………………………………20
Методический лист
Тема 1.6 «Угловая и линейная скорости вращения. Решение задач»
Вид занятия: комбинированный урок.
Методы обучения: объяснительно-иллюстративный, репродуктивный.
Уровень усвоения информации: первый (узнавание ранее изученных объектов, свойств) + второй (выполнение деятельности по образцу, инструкции или под руководством)
Образовательные цели: изучить особенности при движении тела по окружности и познакомить учащихся с дополнительными характеристиками данного движения (нормальное и тангенциальное ускорение. угловая скорость и ускорение)
угловая скорость и ускорение)
Воспитательные цели: развивать коммуникативные способности через организацию работы в малых группах; создавать содержательные и организационные условия для развития самостоятельности в добывании студентами знаний, скорости восприятия и переработки информации, культуры речи, воспитании настойчивости в достижении цели; формировать умение работать в коллективе, команде.
Развивающие цели: развивать активность студентов, умения анализировать, сравнивать, делать выводы и обобщать.
Формирование требований ФГОС при изучении темы
«Угловая и линейная скорости вращения. Решение задач»
В результате изучения темы обучающийся должен знать:
смысл физических величин: нормальное и тангенциальное ускорение. угловая скорость и ускорение;
вклад российских и зарубежных ученых, оказавших наибольшее влияние на развитие физики.

В результате изучения темы обучающийся должен уметь:
описывать и объяснять результаты наблюдений и экспериментов: изменение направления скорости тела при его движении по окружности;
применять полученные знания для решения физических задач;
использовать новые информационные технологии для поиска, обработки и предъявления информации по физике в компьютерных базах данных и сетях (сети Интернета).
Изучение темы 1.6 способствует формированию у обучающихся следующих общих компетенций:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения задач, оценивать их выполнение и качество.
ОК 5.Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде.
Выписка из тематического плана
дисциплины «Физика»
специальность сестринское дело
Тема 1. 6 6«Угловая и линейная скорости вращения. Решение задач» | Содержание учебного материала | 2 |
Угловая скорость и ускорение. Связь линейной и угловой скорости. Связь линейного и углового ускорения. Применение полученных знаний для решения задач. | ||
Лабораторная работа | — | |
Практическое занятие | — | |
Контрольная работа | — | |
Самостоятельная работа обучающихся: — Работа с электронным приложением к учебнику «Физика 10»; — работа с учебником [1, с. 47-53]; — работа с конспектом лекции. | 1 |
Актуальность изучения темы
Движение тела по окружности или дуге окружности довольно часто встречается в природе и технике. Любое криволинейное движение можно представить приближенно как движение по дугам некоторых окружностей. Можно привести много примеров движений тел, траекторией которых является окружность (движение самолета, описывающего «мертвую петлю», людей на карусели, мотоциклов на поворотах дороги и т. д.). Знакомство с таким движением имеет большое значение.
Любое криволинейное движение можно представить приближенно как движение по дугам некоторых окружностей. Можно привести много примеров движений тел, траекторией которых является окружность (движение самолета, описывающего «мертвую петлю», людей на карусели, мотоциклов на поворотах дороги и т. д.). Знакомство с таким движением имеет большое значение.
Примерная хронокарта занятия по теме «Угловая и линейная скорости вращения. Решение задач»
(время занятия 90 минут)
№ | Этапы занятия | Деятельность | Цель этапа занятия | Оснащение этапа | Мин. | |
преподавателя | студентов | |||||
1 | Орг. | Приветствие. Проверка готовности аудитории. | Дежурный информирует об отсутствующих. Контроль внешнего вида студентов. | Мобилизация внимания, выявление готовности аудитории к занятию. | Журнал группы. | 1 |
2 | Актуализация опорных знаний. | Предоставляет возможность повторить домашнее задание, озвучивает вопрос и заслушивает ответы студентов. | Повторяют домашнее задание, отвечают устно с места. | Выявление степени подготовки студентов к занятию и степень усвоения материала по предыдущей теме. Развитие грамотной речи обучающихся, самоконтроль своих знаний. | Вопросы для устного опроса (Приложение №1) | 10 |
3 | Сообщение темы занятия, постановка цели, обозначение актуальности данной темы. | Сообщает тему занятия, определяет цель, обосновывает значимость изучаемой темы. | Слушают, записывают дату и тему занятия в рабочих тетрадях. | Обозначить цель занятия, заинтересовать обучающихся, сконцентрировать их внимание. | Методическая разработка, мультимедийное оборудование, мультимедийная презентация. | 2 |
4 | Изучение нового материала по плану. | Излагает новый материал, демонстрирует презентацию. | Слушают, конспектируют. | Рассмотреть примеры движения различных тел по дуге окружности, вспомнить величины, характеризующие равномерное движение тела по окружности. Ввести понятие «угловой скорости и ускорения»,рассмотреть связь линейной и угловой скорости. | Методическая разработка (блок информации), мультимедийное оборудование, мультимедийная презентация. | 25 |
5 | Первичное закрепление знаний | Раздает вопросы для первичного закрепления материала. | Отвечают на вопросы. | Первичное закрепление и систематизация материала, ликвидация пробелов в понимании в полученных знаниях. | Методическая разработка, презентация. Приложение №2 | 15 |
6 | Решение задач на расчет кинематических величин | Разбор задачи, алгоритма ее решения. Контролирует решение задач студентами, указывает на ошибки. | Работают на местах и у доски. | Отработать навык решения задач на расчет скорости и центростремительного ускорения. Организация собственной деятельности, выбор типовых методов и способов решения задач, оценка их выполнения. | Физика 9 Разноуровневые самостоятельные и контрольные работы А. | 15 |
7 | Задание на самостоятельную работу. | Раздает контролирующий материал, проводит инструктаж по выполнению работы, определяет время самостоятельной работы студентов. | Слушают преподавателя, задают вопросы. | Развитие скорости восприятия и переработки информации, пунктуальности. | Слайд презентации с инструкциями, задания для самостоятельной работы студентов. | 2 |
8 | С. р. Контроль текущих теоретических и практических знаний, контроль конечного уровня знаний. | Контролирует ход работы, помогает, указывает на ошибки. | Работают в малых группах, используют текст учебника, решают задачи по образцу. | Закрепление материала, формирование умения делать выводы, обобщать. | Задания для итогового контроля. Приложение №3 | 15 |
9 | Итоговый контроль. | Контролирует взаимопроверку, поясняет критерии оценки. | Предоставляют выполненное задание, сопоставляют ответы с эталонами, выставляют оценки. | Закрепление знаний по теме, выявление степени усвоения материала. | Слайд презентации с эталонами ответов и критериями отметки (приложение №4). | 3 |
10 | Подведение итогов занятия, выставление оценок. | Оценивает работу группы в целом, индивидуально, обоснование полученных студентами оценок. | Слушают, задают вопросы, участвуют в обсуждении. | Развитие эмоциональной устойчивости, объективности оценки своих действий, умения работать в малых группах, команде. | Журнал группы. | 1 |
11 | Домашнее задание | Проводит инструктаж по выполнению домашнего задания. | Слушают, записывают, задают вопросы. | Оптимизация самоподготовки, определение объема самостоятельной внеаудиторной работы. | Слайд презентации с дифференцированным домашним заданием. | 1 |
Блок информации
План изложения учебного материала по теме «Угловая и линейная скорости вращения. Решение задач»
1. Вращательное движение твердого тела
2. Угловая скорость
3. Период и частота вращения
4. Связь между линейной и угловой скоростью
Изучение нового материала
1.Вращательное движение вокруг неподвижной оси — еще один частный случай движения твердого тела.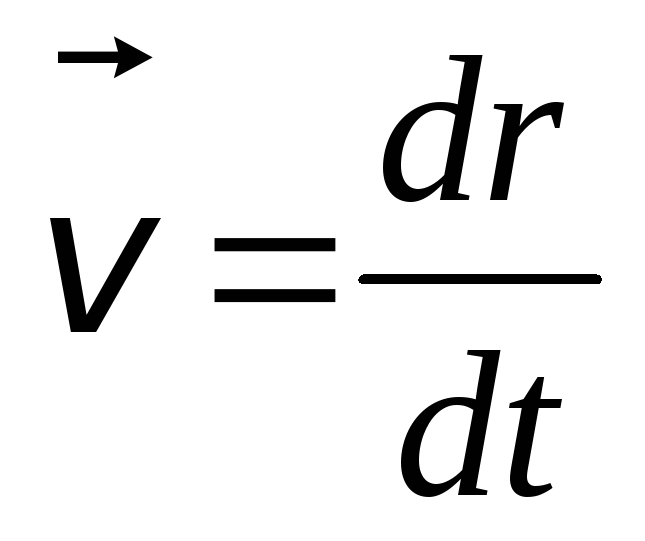
Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4).
В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов.
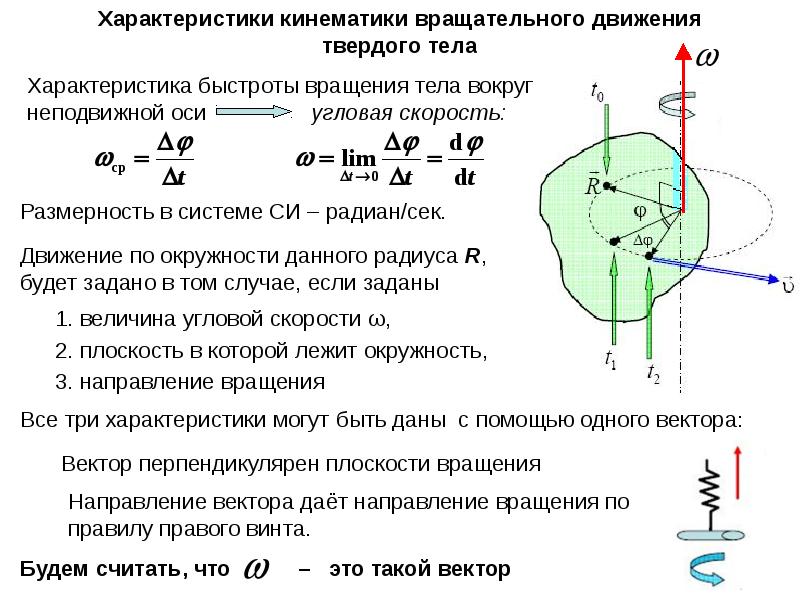
2. Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути. Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол — угол между осью ОХ и радиус-вектором , определяющим положение точки А (см. рис.2.5).
Пусть тело вращается равномерно, т.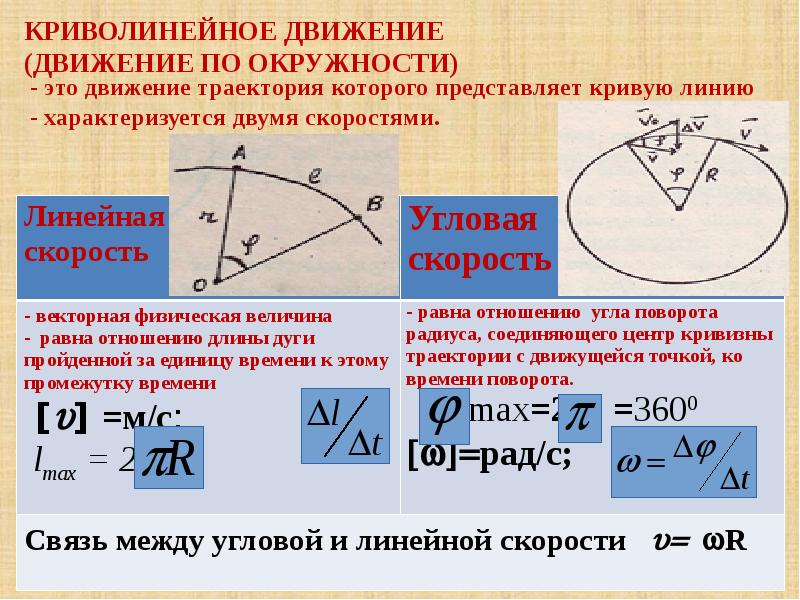 е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое — на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза.
е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое — на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза.
Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению
Угловая скорость выражается в радианах в секунду (рад/с).
Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска — около 140 рад/с1.
3. Угловую скорость можно выразить через частоту вращения, т. е. число полных оборотов за 1с.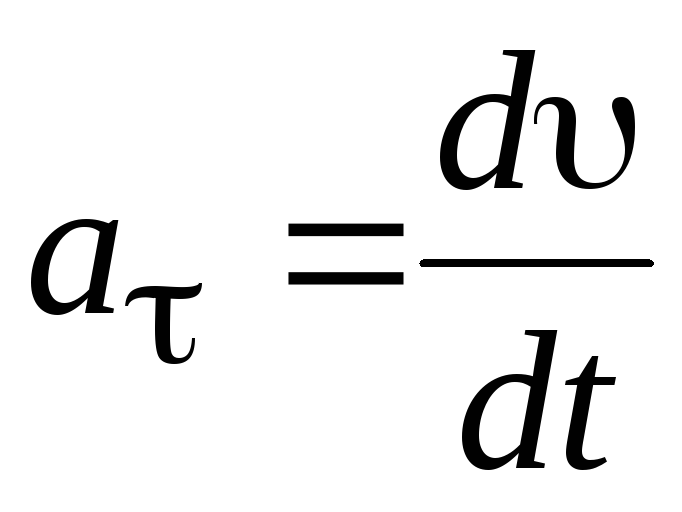 Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:
Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:
Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1)
Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2.1) равен:
Если , то , или .
Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается.
Тем самым мы можем описать положение точек вращающегося тела в любой момент времени.
Связь между линейной и угловой скоростями.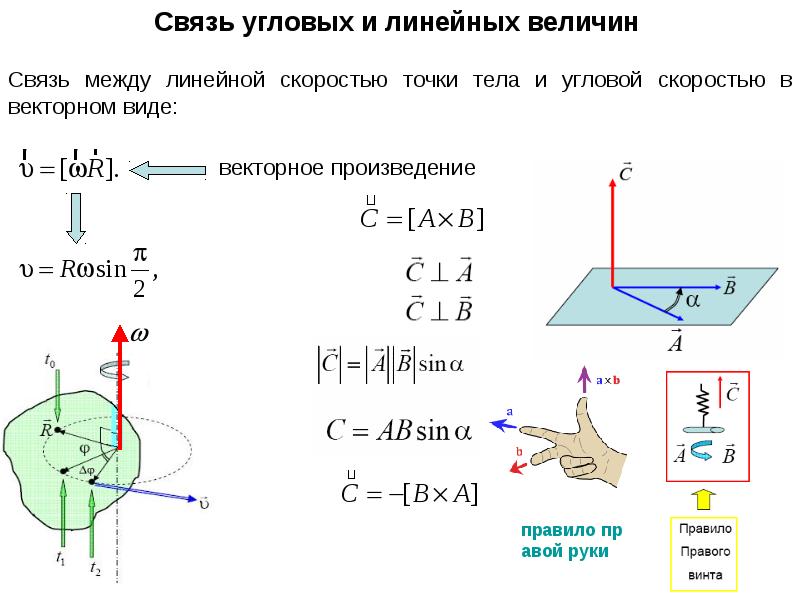 Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.
Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.
Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.
Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:
Так как , то
Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли .
Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:
Следовательно,
Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет.
Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами, можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени. Знаем мы и направления и , a также форму траекторий точек.
План самостоятельной работы студентов
Тема «Угловая и линейная скорости вращения. Решение задач»
№ | Название этапа | Описание этапа | Цель | Время |
1 | Актуализация опорных знаний. | Фронтальный опрос домашнего задания. Приложение №1. | Выявление степени усвоения материала по предыдущей теме. | 10 |
2 | Первичное закрепление знаний. | Самостоятельно отвечают на вопросы, затем вслух формулируют ответы к ним. Приложение№2. | Закрепление полученных знаний, формирование умений анализировать, сравнивать и обобщать. | 15 |
3 | Решение расчетных задач. | Самостоятельное решение задачи по образцу. Физика 9 Разноуровневые самостоятельные и контрольные работы А. Кирик стр. 42 № 3,6, стр. 42 № 1,2, 3 дост. уровень | Отработка навыка решения задач по теме. | 15 |
4 | Контроль конечного уровня знаний. | Выполнение задания для итогового контроля. Приложение№3. Взаимопроверка. Приложение №4. | Контроль усвоения знаний и умений учащихся. Выработка умения оценивать конечный результат выполнения заданий. Выявление степени достижения цели занятия. | 15 |
Приложение №1
Устный опрос по теме «Равномерное движение точки по окружности»
Как направлена мгновенная скорость при криволинейном движении?
Что называется линейной скоростью тела при его движении по окружности?
Что называется периодом и частотой обращения? В каких единицах они измеряются?
Как эти величины связаны между собой?
Как направлено ускорение тела, движущегося по окружности с постоянной по модулю скоростью?
Можно ли считать центростремительное ускорение постоянным, а равномерное движение по окружности равноускоренным?
Если при движении тела по окружности модуль скорости изменяется, будет ли ускорение тела направлено к центру окружности?
Как же можно описать криволинейное движение?
Приложение №2
Вопросы для первичного закрепления знаний
1. Что называется осью вращения твердого тела?
Что называется осью вращения твердого тела?
2. Что такое угловая скорость? Какова ее единица измерения в СИ?
3. Что называют периодом вращения тела (точки)? Единица измерения периода?
4. Что называют частотой вращения тела (точки)? Единица измерения частоты?
5. Какая формула связывает линейную и угловую скорости?
6. Каким соотношением определяется угловое ускорение?
7. Во сколько раз угловая скорость минутной стрелки часов больше угловой скорости часовой стрелки?
Приложение №3
Задания для итогового контроля
1. Тело движется равномерно по окружности по часовой стрелке. Какая стрелка указывает направление вектора линейной скорости при таком движении?
2. Автомобиль движется по окружности радиуса 10 м с центростремительным ускорением 2,5. Какова линейная скорость автомобиля?
3. Поезд движется со скоростью 20 по закруглению дороги. Определите центростремительное ускорение, если радиус дуги равен 40м.
Поезд движется со скоростью 20 по закруглению дороги. Определите центростремительное ускорение, если радиус дуги равен 40м.
4. Колесо велосипеда имеет радиус 40 см. С какой угловой скоростью едет велосипедист, если колесо делает 120 об/мин? Чему равен период вращения колеса?
Приложение №4
Эталоны ответов к заданиям итогового контроля
Номер задания | 1 | 2 | 3 | 4 |
Ответы | 3 | 5 м/с | 10 м/с2 | 4π рад, 2 Гц |
Критерии оценки: за 2 правильно выполненных заданий – «3» балла
За 3 правильно выполненных задания – «4» балла
за 4 правильно выполненных задания – «5» баллов
Домашнее задание
Цель: Определить объем информации для самостоятельной работы, обратить внимание на значимые моменты.
На оценку «3»:Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Соцкий, Физика. 10 класс. Учебник для общеобразовательных учреждений (с приложением на электронном носителе). Базовый и профильный уровни — М.: Просвещение, 2011 г.&19 читать, конспект учить.
На оценку «4»:Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Соцкий, Физика. 10 класс. Учебник для общеобразовательных учреждений (с приложением на электронном носителе). Базовый и профильный уровни — М.: Просвещение, 2011 г.&19 читать, пересказ, конспект учить.
На оценку «5»:Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Соцкий, Физика. 10 класс. Учебник для общеобразовательных учреждений (с приложением на электронном носителе). Базовый и профильный уровни — М.: Просвещение, 2011 г.&19 читать, пересказ, конспект учить. Приготовить выступление на 3-5 минут по теме «Вращательное движение твердого тела».
Перечень оборудования и оснащения
1. Доска
Доска
2. Компьютерное и мультимедийное оборудование
3. Электронное учебное пособие (приложение к учебнику)
4. Мультимедийная презентация
5. Задания для первичного закрепления знаний и итогового контроля
Литература
Основные источники:
Физика. 10 класс [Текст]: учебник для общеобразоват. учреждений с прил. на электрон.носителе: базовый и профил. уровни / Г. Я. Мякишев, Б. Б. Буховцев, Н.Н. Соцкий.-11-е изд. — М. : Просвещение, 2011. – 336 с.
Физика. Задачник. 10-11 кл. [Текст]: пособие для общеобразоват. учреждений / А. П. Рымкевич. – 9-е изд., стереотип. – М.: Дрофа, 2005. – 188 с.
Дополнительные источники:
1. Электронное учебное пособие (приложение к учебнику Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Соцкий, Физика. 10 класс)
2. Физика-9. Разноуровневые самостоятельные и контрольные работы [Текст] / Л. А. Кирик ; — Харьков: «Гимназия», 2001. – 191 с.
А. Кирик ; — Харьков: «Гимназия», 2001. – 191 с.
10
Конвертер угловой скорости и частоты вращения • Механика • Компактный калькулятор • Онлайн-конвертеры единиц измерения
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту
Общие сведения
Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.
В системе СИ угловое ускорение измеряют в радианах в секунду.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины
Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости
У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Угловая скорость и хранение данных на оптических носителях
Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4 200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15 000 оборотов в минуту на высокоэффективных серверах
Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.
Угловая скорость в космосе
Геостационарная орбита
На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники. Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Спутниковые антенны
Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.
УГЛОВАЯ СКОРОСТЬ — это… Что такое УГЛОВАЯ СКОРОСТЬ?
- УГЛОВАЯ СКОРОСТЬ
УГЛОВАЯ СКОРОСТЬ, скорость изменения угловой позиции предмета относительно фиксированной точки.
 Средняя величина угловой скорости w предмета, движущегося от угла q1 до угла q2 за время t выражается как (q2-q1)w)/t. Мгновенной угловой скоростью называют величину, к которой приближается , когда t стремится к нулю. Направление, в котором определяют угловую скорость предмета, перпендикулярно плоскости его движения. Линейная скорость v предмета, находящегося на расстоянии r от фиксированной точки, прямо пропорциональна его угловой скорости: v=rw.
Средняя величина угловой скорости w предмета, движущегося от угла q1 до угла q2 за время t выражается как (q2-q1)w)/t. Мгновенной угловой скоростью называют величину, к которой приближается , когда t стремится к нулю. Направление, в котором определяют угловую скорость предмета, перпендикулярно плоскости его движения. Линейная скорость v предмета, находящегося на расстоянии r от фиксированной точки, прямо пропорциональна его угловой скорости: v=rw.
Научно-технический энциклопедический словарь.
- УГЛИСТЫЙ ЖЕЛЕЗНЯК
- УГЛОВОЕ РАССТОЯНИЕ
Смотреть что такое «УГЛОВАЯ СКОРОСТЬ» в других словарях:
Угловая скорость — Размерность T −1 Единицы измерения … Википедия
УГЛОВАЯ СКОРОСТЬ — векторная величина, характеризующая быстроту вращения твёрдого тела.
 При равномерном вращении тела вокруг неподвижной оси численно его У. с. w=Dj/Dt, где Dj приращение угла поворота j за промежуток времени Dt, а в общем случае w=dj/dt. Вектор У.… … Физическая энциклопедия
При равномерном вращении тела вокруг неподвижной оси численно его У. с. w=Dj/Dt, где Dj приращение угла поворота j за промежуток времени Dt, а в общем случае w=dj/dt. Вектор У.… … Физическая энциклопедияУГЛОВАЯ СКОРОСТЬ — УГЛОВАЯ СКОРОСТЬ, величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости w=Dj/Dt, где Dj приращение угла поворота за промежуток времени Dt … Современная энциклопедия
УГЛОВАЯ СКОРОСТЬ — векторная величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости , где приращение угла поворота за промежуток времени ?t … Большой Энциклопедический словарь
угловая скорость — Кинематическая мера вращательного движения тела, выражаемая вектором, равным по модулю отношению элементарного угла поворота тела к элементарному промежутку времени, за который совершается этот поворот, и направленным вдоль мгновенной оси… … Справочник технического переводчика
угловая скорость — векторная величина, характеризующая быстроту вращения твердого тела.
 При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости ω = Δφ/Δt, где Δφ приращение угла поворота за промежуток времени Δt. * * * УГЛОВАЯ … Энциклопедический словарь
При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости ω = Δφ/Δt, где Δφ приращение угла поворота за промежуток времени Δt. * * * УГЛОВАЯ … Энциклопедический словарьугловая скорость — kampinis greitis statusas T sritis automatika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus. угловая скорость, f pranc. vitesse angulaire, f … Automatikos terminų žodynas
угловая скорость — kampinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis, lygus kūno pasisukimo kampo pirmajai išvestinei pagal laiką: ω = dφ/dt; čia dφ – pasisukimo kampo pokytis, dt – laiko tarpas. Kai kūnas sukasi tolygiai … Penkiakalbis aiškinamasis metrologijos terminų žodynas
угловая скорость — kampinis greitis statusas T sritis fizika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus.
 угловая скорость, f pranc. vitesse angulaire, f … Fizikos terminų žodynas
угловая скорость, f pranc. vitesse angulaire, f … Fizikos terminų žodynasУгловая скорость — величина, характеризующая быстроту вращения твёрдого тела. При равномерном вращении тела вокруг неподвижной оси численно его У. с. ω =Δφ/ Δt, где Δφ приращение угла поворота φ за промежуток времени Δt. В общем случае У. с. численно равна… … Большая советская энциклопедия
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.TAGS}}
{{$item}}
{{l10n_strings. PRODUCTS}}
PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}}
{{$select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}}
{{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
единиц вращательной кинематики | Безграничная физика
Угловое положение, Тета
Угол поворота — это величина (угол) поворота фигуры относительно фиксированной точки — часто центра круга.
Цели обучения
Оценить взаимосвязь между радианами на обороте CD
Основные выводы
Ключевые моменты
- Длина дуги Δs — это расстояние, пройденное по круговой траектории.r — радиус кривизны круговой траектории.
- Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота [латекс] \ Delta \ theta [/ latex] как отношение длины дуги к радиусу кривизны: [latex] \ Delta \ theta [/ latex] = Δs / r.
- За один полный оборот угол поворота составляет 2π.
Ключевые термины
- Угловое положение : угол в радианах (градусах, оборотах), на который точка или линия были повернуты в указанном направлении вокруг указанной оси.
Когда объекты вращаются вокруг некоторой оси, например, когда компакт-диск вращается вокруг своего центра, каждая точка объекта следует по дуге окружности. Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота [latex] \ Delta \ theta [/ latex] как отношение длины дуги к радиусу кривизны:
[латекс] \ Delta \ theta = \ Delta \ text {s} / \ text {r} [/ latex] (показано на).
Угол поворота : Все точки на компакт-диске перемещаются по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δ за время Δt.
В математике угол поворота (или угловое положение) — это величина (т.е. угол), на которую фигура поворачивается относительно фиксированной точки (часто центра круга, как показано на рисунке).
Угол θ и длина дуги s : Радиус круга поворачивается на угол Δ.Длина дуги Δs указана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории. r — радиус кривизны круговой траектории. Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r. Окружность круга равна 2πr. Таким образом, за один полный оборот угол поворота составляет:
[латекс] \ Delta \ theta = (2 \ pi \ text {r}) / \ text {r} = 2 \ pi [/ latex].
Этот результат является основой для определения единиц измерения углов поворота в радианах (рад), определяемых следующим образом:
2π рад = 1 оборот.
Если [latex] \ Delta \ theta [/ latex] = 2π rad, то компакт-диск сделал один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге 360º или один оборот, отношение между радианами и градусами, таким образом, составляет 2π рад = 360º, так что:
1рад = 360º / 2π = 57,3º.
Угловая скорость, Омега
Угловая скорость ω — это скорость изменения угла, математически определяемая как ω = [latex] \ Delta \ theta [/ latex] [latex] / \ Delta \ text {t} [/ latex].
Цели обучения
Проверить, насколько быстро объект вращается на основе угловой скорости
Основные выводы
Ключевые моменты
- Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость.
- Угловая скорость ω аналогична линейной скорости v.
- Мы можем записать взаимосвязь между линейной скоростью и угловой скоростью двумя разными способами: v = rω или ω = v / r.
Ключевые термины
- угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
Чтобы проверить, насколько быстро объект вращается, мы определяем угловую скорость ω как скорость изменения угла. В символах это
.
[латекс] \ omega = \ Delta \ theta / \ Delta \ text {t} [/ latex],
, где угловой поворот Δ происходит за время Δt. Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω аналогична линейной скорости v.Чтобы найти точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещает дугу на длину Δs за время Δt, поэтому она имеет линейную скорость v = Δs / Δt.
Из [latex] \ Delta \ theta = (\ Delta \ text {s}) / \ text {r} [/ latex] мы видим, что [latex] \ Delta \ text {s} = \ text {r} \ cdot \ Дельта \ тета [/ латекс]. Подстановка этого в выражение для v дает [latex] \ text {v} = (\ text {r} \ cdot \ Delta \ theta) / (\ Delta \ text {t}) = \ text {r} (\ Delta \ theta / \ Delta \ text {t}) = \ text {r} \ omega [/ latex].
Мы можем записать это соотношение двумя разными способами: v = rω или ω = v / r.
Первое соотношение утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, она является наибольшей для точки на ободе (наибольшее значение r), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью. Вторую взаимосвязь можно проиллюстрировать, рассмотрев шину движущегося автомобиля, как показано на рисунке ниже. Обратите внимание, что скорость точки в центре шины такая же, как скорость v автомобиля.Чем быстрее движется автомобиль, тем быстрее вращается шина — большой v означает большой ω, потому что v = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет создавать для автомобиля большую линейную скорость (v).
Угловая скорость : Автомобиль, движущийся со скоростью v вправо, имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси равна v, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = rω, где r — радиус шины.Чем больше угловая скорость шины, тем больше скорость автомобиля.
Угловое ускорение, Alpha
Угловое ускорение — это скорость изменения угловой скорости, математически выражаемая как [latex] \ alpha = \ Delta \ omega / \ Delta \ text {t} [/ latex].
Цели обучения
Объясните взаимосвязь между угловым ускорением и угловой скоростью
Основные выводы
Ключевые моменты
- Чем быстрее происходит изменение угловой скорости, тем больше угловое ускорение.
- При круговом движении линейное ускорение касается окружности в интересующей точке и называется касательным ускорением.
- При круговом движении центростремительное ускорение относится к изменению направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение.
Ключевые термины
- угловое ускорение : Скорость изменения угловой скорости, часто обозначаемая α.
- тангенциальное ускорение : ускорение в направлении, касательном к окружности, в интересующей точке при круговом движении.
Угловое ускорение — это скорость изменения угловой скорости. В единицах СИ он измеряется в радианах на секунду в квадрате (рад / с 2 ) и обычно обозначается греческой буквой альфа ([латекс] \ альфа [/ латекс]).
Рассмотрим следующие ситуации, в которых угловая скорость непостоянна: когда фигурист тянет за руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается, когда он выключен.Во всех этих случаях существует угловое ускорение, при котором изменяется [латекс] \ омега [/ латекс]. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:
[латекс] \ alpha = \ Delta \ omega / \ Delta \ text {t} [/ latex]
где [latex] \ Delta \ omega [/ latex] — это изменение угловой скорости, а [latex] \ Delta \ text {t} [/ latex] — это изменение во времени.Единицы углового ускорения: (рад / с) / с или рад / с 2 . Если [latex] \ omega [/ latex] увеличивается, то [latex] \ alpha [/ latex] положительно. Если [latex] \ omega [/ latex] уменьшается, тогда [latex] \ alpha [/ latex] отрицательно.
Полезно знать, как связаны линейное и угловое ускорение. При круговом движении есть ускорение, которое составляет касательных к окружности в интересующей точке (как показано на диаграмме ниже). Это ускорение называется тангенциальным ускорением , a t .
Тангенциальное ускорение : При круговом движении ускорение может происходить из-за изменения величины скорости: a касается движения. Это ускорение называется тангенциальным ускорением.
Касательное ускорение относится к изменениям величины скорости, но не ее направления. При круговом движении центростремительное ускорение, a c , относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение (как показано на диаграмме ниже.) Таким образом, t и c перпендикулярны и независимы друг от друга. Касательное ускорение a t напрямую связано с угловым ускорением и связано с увеличением или уменьшением скорости (но не ее направлением).
Центростремительное ускорение : Центростремительное ускорение возникает при изменении направления скорости; он перпендикулярен круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Угловая и линейная скорость
и об / мин
Purplemath
По какой-то причине учебники часто обращаются к вопросам угловой скорости, линейной скорости и оборотов в минуту (об / мин) вскоре после объяснения секторов круга, их площади и длины дуги.
Длина дуги — это расстояние до части окружности; и линейное расстояние, которое преодолевает, скажем, велосипед, связано с радиусом шин велосипеда.Если вы отметите одну точку на передней шине велосипеда (скажем, точку напротив клапана шины) и посчитаете, сколько раз колесо вращается, вы можете найти количество окружностей окружности, на которые переместилась отмеченная точка.
MathHelp.com
Если вы «раскрутите» эти окружности, чтобы получить прямую линию, то вы найдете расстояние, которое проехал велосипед.Я думаю, что именно такая взаимосвязь между различными показателями и является причиной того, что эта тема часто возникает на данном этапе исследования.
Во-первых, нам нужна техническая терминология и определения.
«Угловая скорость» — это показатель поворота в единицу времени. Он сообщает вам размер угла, под которым что-то вращается за определенный промежуток времени. Например, если колесо вращается шестьдесят раз за одну минуту, то его угловая скорость составляет 120π радиан в минуту.Затем угловая скорость измеряется в радианах в секунду, греческая строчная омега (ω) часто используется в качестве ее названия.
«Линейная скорость» — это мера расстояния в единицу времени. Например, если колесо в предыдущем примере имеет радиус 47 сантиметров, то каждый проход по окружности составляет 94π см, или около 295 см. Поскольку колесо совершает шестьдесят таких оборотов за одну минуту, общая пройденная длина составляет 60 × 94 & pi = 5640π см, или около 177 метров, за одну минуту.(Это примерно 10,6 км / ч или около 6,7 миль / ч)
«Число оборотов в минуту», обычно сокращенно «об / мин», является мерой вращения за единицу времени, но единица времени — всегда одна минута. И вместо того, чтобы указывать угол поворота, он просто дает количество поворотов. Когда вы смотрите на тахометр на приборной панели автомобиля, вы смотрите на текущие обороты двигателя автомобиля. В приведенном выше примере частота вращения будет просто «60».
«Частота» f — это мера вращения (или вибрации) за единицу времени, но единицей времени всегда является одна секунда.Единицей измерения частот является «герц», который обозначается как Гц.
Соотношение между частотой f (в Гц), об / мин и угловой скоростью ω (в радианах) показано ниже (все элементы в любой строке эквивалентны):
Однако вы можете обнаружить, что «угловая скорость» используется как взаимозаменяемые (но только неофициально; не учеными) с оборотами в минуту или частотой. Кроме того, некоторые (например, физики) считают, что «угловая скорость» является векторной величиной, а ω — скалярной величиной, называемой «угловой частотой».
Пожалуйста, не запоминайте эти потенциальные слияния и не беспокойтесь о том, какими могут быть «векторы» или «скаляры». Я говорю вам об этом, чтобы предупредить вас, что вы должны уделять очень пристальное внимание тому, как ваш конкретный учебник и ваш конкретный преподаватель определяют различные термины для этого конкретного класса. И знайте, что на следующем уроке термины и определения могут быть другими.
Колесо имеет диаметр 100 сантиметров.Если колесо поддерживает тележку, движущуюся со скоростью 45 километров в час, то какова частота вращения колеса с точностью до целого числа оборотов в минуту?
«Об / мин» — это количество оборотов колеса в минуту. Чтобы выяснить, сколько раз это колесо вращается за одну минуту, мне нужно найти (линейное или прямое) расстояние, пройденное (за минуту) при движении со скоростью 45 км / ч. Затем мне нужно будет найти длину окружности колеса и разделить общее поминутное (линейное) расстояние на это «разовое» расстояние.Количество окружностей, которые умещаются в пределах общего расстояния, — это количество оборотов колеса за этот период времени.
Сначала я переведу (линейную) скорость тележки из км / ч в «сантиметры в минуту», используя то, что я узнал о преобразовании единиц. (Почему «сантиметры в минуту»? Потому что я ищу «обороты в минуту», поэтому минуты — лучшая единица времени, чем часы. Кроме того, диаметр дан в сантиметрах, так что это лучшая единица длины, чем километры.)
Итак, расстояние, пройденное за одну минуту, составляет 75 000 сантиметров. Диаметр колеса — 100 см, поэтому радиус — 50 см, а длина окружности — 100π см. Сколько из этих окружностей (или оборотов колеса) умещается внутри 75 000 см? Другими словами, если бы я снял протектор этого колеса с тележки и разложил его ровно, то получилось бы расстояние 100π см. Сколько из этих длин укладывается на все расстояние, пройденное за одну минуту? Чтобы узнать, сколько из (этого) помещается в такое количество (этого), я должен разделить (это) на (это), так что:
Затем, округляя до ближайшего целого числа оборотов (то есть округляя ответ до целого числа), мой ответ:
Примечание. Эта скорость не такая высокая, как может показаться: чуть меньше четырех оборотов в секунду.Вы можете сделать это на своем велосипеде, не вспотев. Вот еще одно примечание: источник, из которого я получил свою схему для вышеупомянутого упражнения, использовал «угловую скорость» и «ω» для «числа оборотов в минуту». Да, в учебнике алгебры использовались неправильные единицы измерения.
Предыдущее упражнение давало информацию о скорости автомобиля и колесе. Отсюда мы нашли количество оборотов в минуту. Мы можем пойти и другим путем; мы можем начать с числа оборотов в минуту (плюс информацию о колесе) и найти скорость транспортного средства.
Велосипедное колесо имеет диаметр 78 см. Если колесо вращается со скоростью 120 оборотов в минуту, какова линейная скорость велосипеда в километрах в час? Ответ округлите до одного десятичного знака.
Линейная скорость — это расстояние по прямой, которое велосипед проходит за определенный период времени.Они дали мне количество оборотов колеса в минуту. Фиксированная точка на шине (скажем, камешек на протекторе шины) перемещает длину окружности за каждый оборот. Раскручивая это расстояние по земле, велосипед будет двигаться по земле на одинаковое расстояние, по одной окружности за раз, за каждый оборот. Итак, в этом вопросе меня просят найти длину окружности, а затем использовать ее, чтобы найти общее расстояние, пройденное за минуту.
Так как диаметр равен 78 см, то окружность равна C = 78π см.Разматывая путь шины до прямой линии на земле, это означает, что велосипед перемещается на 78π см вперед за каждый оборот шины. Таких оборотов в минуту 120, итого:
(78π см / об) × (120 об / мин) = 9,360π см / мин
Теперь мне нужно преобразовать это из сантиметров в минуту в километры в час:
Велосипед движется со скоростью около 17,6 км / ч.
… или около одиннадцати миль в час.
Предположим, что орбита Земли круговая с радиусом 93 000 000 миль, и пусть «один год» равен 365,25 дням. В этих условиях найдите линейную скорость Земли в милях в секунду. Ответ округлите до одного десятичного знака.
Скорость — это (линейное или эквивалентное прямолинейное) расстояние, пройденное за одну секунду, деленное на одну секунду.Они дали мне информацию за год, так что я начну с этого. Окружность круга с r = 93000000 миль будет линейным расстоянием, которое Земля преодолеет за один год.
C = 2π (93000000 миль) / год = 186000000π миль / год
Это количество миль, пройденных за один год, но мне нужно количество миль, пройденных за одну секунду. В сутках двадцать четыре часа, в часе шестьдесят минут и в минуте шестьдесят секунд, поэтому общее количество секунд в этом году составляет:
Тогда линейная скорость, представляющая собой общее линейное расстояние, деленное на общее время и выраженное в единицах скорости, равна:
Тогда, округленная до одного десятичного знака, линейная скорость Земли равна:
«Эй!» Я слышу, как ты плачешь.»Когда мы собираемся использовать угловые меры для чего-нибудь?» Хотя многие («большинство»?) Упражнений в вашей книге, вероятно, будут похожи на приведенные выше, иногда вы можете столкнуться с фактическими радианами и градусами.
Поезд движется со скоростью 10 миль в час по кривой радиусом 3000 футов. На какой угол повернется поезд за одну минуту? Округлить до ближайшего целого числа градусов.
«Кривая радиуса 3000 футов» означает, что, если бы я попытался плотно подогнать круг внутри кривой, наилучшим образом подошел бы круг с радиусом r = 3000 футов.Другими словами, я могу использовать факты круга, чтобы ответить на этот вопрос.
Поскольку радиус кривой выражен в футах и мне нужно найти угол, пройденный за одну минуту, я начну с преобразования скорости миль в час в футы в секунду:
(10 миль / час) (5280 фут / миль) (1 час / 60 мин) = 880 фут / мин
Длина изогнутого пути, который проходит поезд, также является частью окружности круга.Итак, эти 880 футов — это длина дуги, и теперь мне нужно найти дополнительный угол (подразумеваемого) сектора круга:
Но это значение в радианах (потому что это то, что использует формула длины дуги), и мне нужно, чтобы мой ответ был в градусах, поэтому мне нужно преобразовать:
Поезд поворачивает на угол примерно:
Представьте, что вы стоите в центре этого воображаемого круга (то есть на расстоянии трех тысяч футов от поворота, более чем в полумиле) и наблюдаете, как поезд движется по повороту.Если вы протянете руку на расстоянии вытянутой руки, сожмете кулак и, крепко прижав средние пальцы большим пальцем вниз, приподнимите мизинец и указательный пальцы, расстояние между ними составит около пятнадцати градусов. Поезд вряд ли продвинется дальше. Если бы вы держали кулак на расстоянии вытянутой руки и вытянули мизинец и большой палец, расстояние было бы примерно двадцать пять градусов. Поезд не выйдет из ваших пальцев в отведенное время.
(Иногда я узнаю самые крутые вещи, когда исследую проблемы со словами.Опять же, мое определение «крутого» может быть немного грустным ….)
URL: https://www.purplemath.com/modules/sectors3.htm
Определение линейной и угловой скорости
Показать стенограмму
Ее совет, это мама в туре P, убери это спокойствие.Хорошо, сегодня я собираюсь поговорить о линейной скорости в зависимости от угловой скорости. Итак, когда вы двигаетесь по кругу, вас привлекают вещи, которые меняются. Итак, первое, что похоже на движение, — это как движение по прямому пути, это то, что ваше положение меняется относительно времени. Так, например, если вы движетесь вправо, и мы считаем правильное направление положительным. Так что по мере того, как вы двигаетесь вправо, ваша позиция становится все больше и больше в положительном направлении. Таким образом, скорость изменения вашего положения называется линейной скоростью или, по сути, скоростью изменения вашего положения относительно языка.Итак, в этом случае, когда вы двигаетесь по кругу, то же самое происходит и с вашей позицией. Предположим, что вы начинаете с точки а здесь, на единичной окружности. А затем вы переходите к точке B. Итак, по мере того, как вы переходите от A к B, ваше расстояние или ваше положение в основном меняются, и это вроде как длина дуги вашего положения меняется. Поэтому, когда вы приближаетесь к точке B, вы двигаетесь дальше или по кругу. Таким образом, вы получаете большую длину дуги по мере того, как вы приближаетесь к большой.Таким образом, другая вещь, которая меняется помимо вашего положения, — это угол, который измеряется от положения до начала координат, например, если вы находитесь в разных положениях между a и b. Таким образом, вы испытаете разные меры углов. Скажем, угол альфа и угол тета. Если вы, например, находитесь в точке C и точке D. Итак, две вещи меняют ваше положение, которое находится на круге. Вот как быстро ваше положение меняется с той, с которой мы приближаемся к скорости. И еще одна вещь, которая меняется, — это угол, отсчитываемый от начала координат, и скорость его изменения называется угловой скоростью.В основном мы говорим об изменении позиции. Мы называем это одной. Мы называем это одной линейной скоростью. По сути, мы можем сказать, что Дуга связана с течением времени. А затем изменится центральный угол, который в основном представляет собой угловую скорость. И это на самом деле можно показать с помощью дельта-тета во времени или дельта-альфа во времени, как бы мы это ни называли. Таким образом, в этом случае происходит преобразование между линейной скоростью и угловой скоростью. Как вы знаете, у нас есть формула для длины дуги. Связанная дуга — это в основном радиус, умноженный на угол тета.И это 40 пап. Мы измеряем тэту от 0. Хорошо, так как мы измеряем тэту от 0. И также обратите внимание, что это должна быть жена в радианах, а не в градусах. Это действительно важно. Теперь, используя эту формулу, мы собираемся получить соотношение между линейной скоростью и угловой скоростью. Таким образом, угловую длину дуги можно назвать S равной r, умноженному на theta. Теперь, если я беру производную или смотрю на изменение связанной дуги и тета ri относительно времени, я могу фактически изменить это отношение на дельту S, равную R, умноженному на дельта тета.Итак, в основном мы знаем, что радиус постоянен, когда мы движемся по окружности. Так что радиус не меняется. Так что единственное, что меняется. Один из них — ваше положение, длина дуги или центральный угол при движении. Таким образом, мы можем сказать, что изменение длины дуги или изменение положения равно радиусу, умноженному на изменение центрального угла в 3D. Теперь, если я разделю обе стороны на дельту t, то я могу сказать, что дельта S по сравнению с дельтой T равна r, умноженному на дельта тета по сравнению с дельтой t. Так что я бы получил те же определения, которые написал для Эрика наверху.Таким образом, дельта S по сравнению с дельтой T — это изменение положения относительно времени, которое я могу назвать одной линейной скоростью. И затем R умножает изменение угла относительно времени. Я могу назвать это омегой или угловой скоростью. Итак, я получил соотношение между линейной и угловой скоростью. Хорошо. Теперь давайте сделаем один пример и посмотрим, как он работает. Итак, мы рассматриваем объект, движущийся по единичной окружности, движущийся по единичной окружности. Итак, как мы знаем, единичный круг означает оценку DSP на единицу. Хорошо, и он движется вместе с деревом на метр в секунду.Таким образом, линейная скорость составляет три метра в секунду. И они спрашивают нас, как быстро меняется угол или центральный угол, когда этот объект вращается. Так как мы получили V ii равняется омеге советского засорения трем метрам в секунду. А для радиуса, скажем, радиус составляет один метр на один метр умноженный на омега. По мере того, как я упрощаю единицы, я получу омега-равное дерево. Один за секунду. Так что в основном единица измерения — только секунда. Общее в стандартном способе выражения единицы для омеги — это в основном радиан в секунду, но будьте осторожны, радиан — это не единица измерения, это просто способ измерения угловых градусов и радиантных единиц R-ноль.Итак, когда вы видите, что угловая скорость равна некоторому числу радиан в секунду. Фактическая единица угловой скорости — просто секунда. Итак, как видите, мы получили омегу или угловую скорость. Точно так же, если дана омега и вы знаете радиус, вы можете найти линейную скорость. И если задана линейная скорость, вы можете найти омегу, которая представляет собой очень простую и простую связь между линейной скоростью и угловой скоростью. Еще одна вещь, о которой я должен упомянуть, — это омега или угловая скорость могут быть положительными или отрицательными так же, как и линейная скорость.Итак, если вы двигаетесь по часовой стрелке по ЕС по кругу, угловое изменение угла будет отрицательным. Таким образом, вы движетесь в отрицательном направлении углов. Итак, омега будет отрицательной. И если вы двигаетесь против часовой стрелки, очевидно, изменение угла будет положительным. И у вас будет положительная угловая скорость. Я надеюсь, что это в основном то, что вам всем понравилось и вы узнали то, что я объяснил. Надеюсь, вам понравится последовательность видео, которую я загружаю сюда.В будущем я затрону еще несколько тем. Наверное, хотелось бы больше трюков и некоторых расчетов. Так что, пожалуйста, следите за всеми видео, и я надеюсь, что вам понравилось, и хорошего дня
Линейная и угловая скорости связаны со скоростью объекта в зависимости от взятой перспективы. Линейная скорость применяется к любому движущемуся объекту или частице, в то время как угловая скорость применяется к тем, которые вращаются (например, колесо, вращение земли или волчок). Угловая скорость является выражением углового смещения во времени и может быть выражена в градусах или радианах (радианах в час, градусах в секунду и т. Д.).Угловая скорость находится с помощью уравнения. Чтобы определить линейную скорость (линейное смещение во времени) из угловой скорости, примените формулу, где ω выражается в радианах / время, а r — радиус пройденного пути (или радиус объекта, если он спиннинг).
См. Дополнительные разделы по тригонометрии
Как рассчитать формулу угловой скорости
Формула угловой скорости: В физике угловая скорость относится к тому, насколько быстро объект вращается или вращается относительно другой точки, т.е.е. насколько быстро угловое положение или ориентация объекта меняется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и угловая скорость вращения. Угловая скорость вращения означает, насколько быстро твердое тело вращается относительно центра вращения.
Орбитальная угловая скорость относится к тому, насколько быстро точечный объект вращается вокруг фиксированного начала координат, то есть скорость изменения его углового положения относительно начала координат во времени. Как правило, угловая скорость измеряется в углах в единицу времени, т.е.грамм. радиан в секунду. Единица измерения угловой скорости в системе СИ выражается в радианах / сек, причем радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ представлены как 1 / сек . Угловая скорость обычно обозначается символом омега ( ω , иногда Ω ). По соглашению, положительная угловая скорость означает вращение против часовой стрелки, а отрицательная — по часовой стрелке.
Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = 360/24 = 15 градусов в час, или 2π / 24 ≈ 0.26 радиан в час. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega}. Таким образом, с радиусом орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 × 0,26 ≈ 11 000 км / ч. Угловая скорость положительна, поскольку спутник движется на восток вместе с вращением Земли (против часовой стрелки над северным полюсом).
Как рассчитать формулу угловой скорости
В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, а ее направление указывает перпендикулярно плоскости мгновенного вращения или углового смещения.Ориентация угловой скорости условно задается правилом правой руки.
Формула для угловой скорости
В простейшем случае кругового движения по радиусу {\ displaystyle r} с положением, заданным угловым смещением {\ displaystyle \ phi (t)} от оси x, орбитальная угловая скорость — это скорость изменения угла с относительно времени: {\ displaystyle \ omega = {\ tfrac {d \ phi} {dt}}}. Если {\ displaystyle \ phi} измеряется в радианах, расстояние от оси x вокруг круга до частицы равно {\ displaystyle \ ell = r \ phi}, а линейная скорость равна {\ displaystyle v (t) = {\ tfrac {d \ ell} {dt}} = r \ omega (t)}, так что {\ displaystyle \ omega = {\ tfrac {v} {r}}}.
В общем случае частицы, движущейся в плоскости, орбитальная угловая скорость — это скорость, с которой вектор положения относительно выбранного начала координат «выметает» угол. На диаграмме показан вектор положения {\ displaystyle \ mathbf {r}} от начала координат {\ displaystyle O} до частицы {\ displaystyle P} с его полярными координатами {\ displaystyle (r, \ phi)}. (Все переменные являются функциями времени {\ displaystyle t}.) Частица имеет линейное разделение скорости как {\ displaystyle \ mathbf {v} = \ mathbf {v} _ {\ |} + \ mathbf {v} _ {\ perp }} с радиальным компонентом {\ displaystyle \ mathbf {v} _ {\ |}}, параллельным радиусу, и поперечно-радиальным (или тангенциальным) компонентом {\ displaystyle \ mathbf {v} _ {\ perp}} перпендикулярно радиусу.Когда нет радиальной составляющей, частица движется вокруг начала координат по окружности; но когда нет поперечно-радиального компонента, он движется по прямой линии от начала координат. Поскольку при радиальном движении угол остается неизменным, только поперечно-радиальная составляющая линейной скорости вносит вклад в угловую скорость.
Угловая скорость ω — это скорость изменения углового положения относительно времени, которая может быть вычислена из поперечной радиальной скорости как:
- {\ displaystyle \ omega = {\ frac {d \ phi} {dt}} = {\ frac {v _ {\ perp}} {r}}.}
Здесь поперечная радиальная скорость {\ displaystyle v _ {\ perp}} является величиной со знаком {\ displaystyle \ mathbf {v} _ {\ perp}}, положительной для движения против часовой стрелки, отрицательной для движения по часовой стрелке. Если взять полярные координаты для линейной скорости {\ displaystyle \ mathbf {v}}, получаем величину {\ displaystyle v} (линейную скорость) и угол {\ displaystyle \ theta} относительно радиус-вектора; в этих терминах {\ displaystyle v _ {\ perp} = v \ sin (\ theta)}, так что
- {\ displaystyle \ omega = {\ frac {v \ sin (\ theta)} {r}}.{\ perp} = (- y, x)}.
В двух измерениях угловая скорость — это число со знаком плюс или минус, указывающее ориентацию, но не указывающее в направлении. Знак обычно считается положительным, если радиус-вектор вращается против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда угловая скорость может быть названа псевдоскалярной, числовой величиной, которая меняет знак при инверсии четности, такой как инвертирование одной оси или переключение двух осей.
Читайте также: Формула трехчлена идеального квадрата
Как рассчитать угловую скорость на основе числа оборотов в минуту?
оборотов в минуту можно преобразовать в угловую скорость в градусах в секунду, умножив оборотов в минуту на 6, так как один оборот составляет 360 градусов, а это 60 секунд в минуту.Если об / мин равно 1 об / мин , угловая скорость в градусах в секунду будет 6 градусов в секунду, так как 6 умноженное на 1 равно 6.
Какова формула угловой скорости?
Чтобы получить нашу вторую формулу для угловой скорости , мы понимаем, что тета дается в радианах, а определение радианной меры дает theta = s / r. Таким образом, мы можем подставить theta = s / r в нашу первую формулу угловой скорости .Это дает w = (s / r) / t.
Обороты — это то же самое, что и угловая скорость?
Угловая скорость равна скорости вращения . Что-то крутится. Это сокращение от «Оборотов в минуту». Другие связанные единицы, которые выражают то же свойство , — градусы в секунду и радианы в секунду.
Формула средней угловой скорости
Во-первых, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-либо другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругам или их частям.Вы можете вспомнить из геометрии или тригонометрии, что длина окружности равна его диаметру, умноженному на константу пи, или πd . (Значение пи составляет около 3,14159.) Это чаще всего выражается в терминах радиуса круга r , который составляет половину диаметра, в результате чего окружность 2πr .
Кроме того, вы, вероятно, где-то по пути узнали, что круг состоит из 360 градусов (360 °). Если вы переместитесь на расстояние S по окружности, то угловое смещение θ будет равно S / r.Таким образом, один полный оборот дает 2πr / r, что оставляет 2π. Это означает, что углы меньше 360 ° могут быть выражены в единицах пи или, другими словами, в радианах.
Взяв всю эту информацию вместе, вы можете выразить углы или части круга в единицах, отличных от градусов:
1 радиан = (360 ° / 2π) = 57,3 °,
В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно в секунду.
Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r от центра круга, причем направление v всегда перпендикулярно радиусу круга, тогда угловую скорость можно записать
, где ω — греческая буква омега. Единицы угловой скорости — радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v / r дает м / с, деленные на м, или с -1 , что означает, что радианы технически являются безразмерной величиной.
Формула центростремительного ускорения Угловая скорость
Формула углового ускорения выводится так же, как и формула угловой скорости: это просто линейное ускорение в направлении, перпендикулярном радиусу окружности (эквивалентно, его ускорение по касательной к круговой траектории в любой точке) делится на радиус круга или части круга, который составляет:
, потому что для кругового движения a t = ωr / t = v / t.
α , как вы, наверное, знаете, это греческая буква «альфа». Индекс «t» здесь означает «касательную».
Как ни странно, вращательное движение может иметь другой вид ускорения, называемый центростремительным («центростремительным») ускорением. Это дается выражением:
Это ускорение направлено к точке, вокруг которой вращается рассматриваемый объект. Это может показаться странным, поскольку объект не приближается к этой центральной точке, так как радиус r фиксирован.Думайте о центростремительном ускорении как о свободном падении, при котором нет опасности столкновения объекта с землей, потому что сила, притягивающая объект к нему (обычно сила тяжести), точно компенсируется тангенциальным (линейным) ускорением, описываемым первым уравнением в эта секция. Если бы a c не было равно a t , объект либо улетел бы в космос, либо вскоре врезался бы в середину круга.
Читайте также: Средняя и мгновенная скорость изменения
Формула угловой скорости Физика
Прежде чем мы перейдем к угловой скорости, мы сначала рассмотрим линейную скорость. Линейная скорость применяется к объекту или частице, движущимся по прямой линии. Это скорость изменения положения объекта во времени.
Линейная скорость может быть рассчитана по формуле v = с / t , где v = линейная скорость, с = пройденное расстояние и t = время, необходимое для преодоления расстояния. Например, если я проехал 120 миль за 2 часа, то для расчета моей линейной скорости я бы вставил с = 120 миль и t = 2 часа в мою формулу линейной скорости, чтобы получить v = 120 / 2 = 60 миль в час.Один из наиболее распространенных примеров линейной скорости — это ваша скорость при движении по дороге. Ваш спидометр показывает вашу скорость или показатель в милях в час. Это скорость изменения вашего положения относительно времени, другими словами, ваша скорость — это ваша линейная скорость.
Перед тем, как перейти к угловой скорости, нам нужно рассмотреть еще одну вещь — радианы. Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой.Техническое определение радиан. Измерение — это длина дуги, образуемой углом, деленная на радиус круга, частью которого является угол, где протяженность означает, что она противоположна углу и проходит от одной точки на круг к другому, оба отмечены углом. Это говорит нам, что угол theta = с / r радиан, где с = длина дуги, соответствующей тета, и r = радиус круга, частью которого является тета.
Формула угловой скорости в линейную скорость Поскольку большинству из нас комфортно с градусным измерением углов, удобно, что мы можем легко преобразовать градус в радиан, умножив градус на пи / 180. Например, угол 45 градусов имеет мера в радианах 45 (пи / 180), которая равна пи / 4 радиана.
Читайте также: Формула линейной интерполяции
Угловая скорость и линейная скорость — определение, взаимосвязь и часто задаваемые вопросы
Мы знаем, что угловое смещение — это угол, наблюдаемый частицей при круговом движении.Поскольку направление смещения вдоль оси, угловое смещение является осевым вектором.
Частица при круговом движении проявляет два типа смещения; это:
Если ‘r’ — радиус окружности, то соотношение между угловым и линейным смещением будет:
S = Rθ или θ = \ [\ frac {S} {r} \]… .. ( 1)
Линейная скорость определяется как скорость изменения линейного смещения. Для частицы P это определяется как:
v = \ [\ frac {\ Delta S} {\ Delta t} \]….(2)
Угловая скорость частицы — это скорость изменения углового смещения, то есть скорость изменения угла. Он задается следующим образом:
ω = \ [\ frac {\ Delta \ theta} {\ Delta t} \]… (3)
В этой статье мы выведем связь между линейной скоростью и угловой скоростью. Итак, приступим.
Связь между линейной скоростью и угловой скоростью
Мы знаем, что линейная скорость частицы P определяется выражением:
| v | = \ [\ frac {\ Delta (S)} {\ Delta t} \] и S = rθ
Теперь, подставив значение уравнения (1) в (3), мы получим:
v = \ [ \ frac {\ Delta r \ theta} {\ Delta t} \]
Мы знаем, что радиус ‘r’ является постоянным значением, поэтому получаем:
v = \ [\ frac {r \ Delta \ theta} {\ Delta t} \] (Как \ [\ frac {\ Delta \ theta} {\ Delta t} \] = ω)
⇒ | v | = rω, которое представляет собой «соотношение между линейной и угловой скоростью.
Здесь v зависит от r и ω следующим образом:
ω = скорость вращения объекта и
r = линейная скорость частицы в центре будет равна нулю. Когда частица начинает удаляться от центра, линейная скорость начинает увеличиваться. Максимум на окружности круга.
Касательная к окружности определяет направление линейной скорости.
Запомните
Согните пальцы против часовой стрелки, а большой палец, направленный наружу (вдоль оси), определяет направление угловой скорости.Точно так же, если вы согнете пальцы по часовой стрелке, большой палец, направленный внутрь, даст направление ω.
Соотношение угловой скорости и линейной скорости
Для тела, совершающего равномерное круговое движение, соотношение между линейной и угловой скоростью составляет:
v = rω
Это уравнение утверждает, что линейная скорость (v) прямо пропорциональна расстояние частицы от центра кругового пути и ее угловая скорость.
В центре нулевое значение.
Минимум между центром и любой точкой на окружности.
Максимально на окружности круга. Однако угловая скорость остается неизменной во всех точках круговой траектории.
От угловой скорости к линейной
Из наших знаний о круговом движении мы можем сделать вывод, что величина линейной скорости частицы, движущейся по кругу, связана с угловой скоростью частицы следующим соотношением:
r = \ [\ frac {v} {\ omega} \]
В любой момент это соотношение применимо к каждой частице, имеющей твердое тело.
Разница между линейной скоростью и угловой скоростью
Линейная скорость
Угловая скорость
Угловая скорость
Определение скорости изменения линейного перемещения.
Мы определяем угловую скорость как скорость изменения углового смещения.
Ключевые различия
При круговом движении линейная скорость частицы проходит по окружности круга.
Он отличается в разных точках окружности.
Символ
Символ для линейной скорости — v.
Символ угловой скорости — греческая буква, то есть ω (произносится как омега).
Формула
v = \ [\ frac {\ Delta S} {\ Delta t} \] = \ [\ frac {2 \ pi r} {t} \]
ω = \ [\ frac {\ Delta \ theta} {\ Delta t} \] = \ [\ frac {2 \ pi r} {t} \]
Количество
Это векторная величина это означает, что он имеет как величину, так и направление.
Это осевой вектор. Это потому, что направление смещения частицы находится вдоль оси круга.
Измерительный блок
Мы измеряем линейную скорость в м / с.
Мы измеряем угловую скорость как в градусах, так и в радианах.
Градус — безразмерная единица.
Радиан — это единица СИ.
Пример из реальной жизни
Если ваш офис находится на расстоянии 150 км от дома, ваша машина приобретет линейную скорость.{\правая стрелка }\].
Это потому, что v действует на окружность окружности, а ω — вдоль оси. Чтобы векторы двух величин были равны, их направления должны быть одинаковыми. Здесь мы видим, что направления v и ω не равны; вот почему правильный способ записать соотношение:
v = rω
Угловые и линейные скорости — Эрик Скотт Барр
—Тригонометрия
Углы
В этой статье будут рассмотрены объекты, которые вращаются по кругу, и представлены две формы скорости, то есть скорость, с которой объекты движутся относительно времени: угловая и линейная скорости.В первой статье этой серии по тригонометрии угол определяется как один луч, конечная сторона, вращающаяся от другого луча, начальная сторона. Во второй статье две точки этих лучей были закреплены на единичной окружности. Оказывается, такое вращение точки вокруг круга довольно часто встречается в реальном мире.
Угловая скорость
Объекты, которые движутся или вращаются по кругу, являются частью повседневной жизни. Турбины вращаются с высокой скоростью для выработки электричества, лопасти вертолета вращаются для создания подъемной силы, и даже человек, стоящий на Земле, имеет скорость, когда Земля вращается вокруг своей оси и вращается вокруг Солнца.Этот тип скорости известен как угловая скорость , скорость, с которой угол, образованный начальной начальной точкой и текущим местоположением объекта, изменяется с течением времени. Ключевые слова в этом определении: означает , — и — время ; или другими словами дробь.
\ [\ frac {rate} {время} \]
В последней статье установлено, что один оборот вокруг единичной окружности равен $ 2 \ pi $ радианам. Что касается вращения, объект перемещается на $ 2 \ pi $ радиан за каждый 1 оборот.
\ [\ frac {2 \ pi} {1 \ \ text {rev}} \]
Следовательно, угловая скорость $ \ omega $ может быть математически описана как угол $ \ alpha $ в радианах, через который объект движется за время $ t $.
\ [\ omega = \ frac {\ alpha} {t} \]
С этой информацией теперь легко переводить число оборотов во времени в радианы во времени. Чтобы увидеть это в действии, представьте ветряную турбину, лопасти которой вращаются со скоростью 20 оборотов в минуту.
Ветряк вращается
Теперь просто конвертируйте, используя соотношение, которое позволяет отменить желаемые единицы.
\ [\ omega = \ frac {20 \ \ text {rev}} {1 \ \ text {min}} = \ frac {20 \ \ cancel {\ text {rev}}} {1 \ \ text {min}} * \ frac {2 \ pi \ \ text {rad}} {1 \ \ cancel {\ text {rev}}} = \ frac {40 \ pi \ \ text {rad}} {1 \ \ text {min}} \ приблизительно 125,7 \ \ text {рад / мин} \]
Преобразование единиц времени
Предыдущий пример показал обороты в минутах, но что, если необходимо увидеть их в разных единицах времени, например, в секундах или часах? Ответ так же прост, как добавить в уравнение еще один коэффициент преобразования.Взяв предыдущий пример, преобразуйте измерение в секунды. В этом случае конвертируйте минуты и секунды. Это соотношение можно показать двумя способами:
\ [\ frac {1 \ \ text {min}} {60 \ \ text {sec}} \ text {или} \ frac {60 \ \ text {sec}} {1 \ \ text {min}} \]
Какой коэффициент преобразования даст желаемый результат преобразования минут в секунды в предыдущем примере? Для тех, кто обратил внимание на предыдущие статьи этой серии, ответ прост: тот, который позволяет минутам сокращать .Возвращаясь к последнему уравнению, преобразование в секунды может выглядеть так:
\ [\ omega = \ frac {20 \ \ text {rev}} {1 \ \ text {min}} = \ frac {20 \ \ cancel {\ text {rev}}} {1 \ \ cancel {\ text { min}}} * \ frac {2 \ pi \ \ text {rad}} {1 \ \ cancel {\ text {rev}}} * \ frac {1 \ \ cancel {\ text {min}}} {60 \ \ text {sec}} = \ frac {40 \ pi \ \ text {rad}} {60 \ \ text {sec}} \ приблизительно 2,1 \ \ text {rad / sec} \]
Линейная скорость
Линейная скорость во многом аналогична угловой, за исключением того, что линейная скорость согласована с единицами измерения расстояния, которые меняются во времени, а не с мерой углов, изменяющихся во времени.Что касается круга, это расстояние представлено длиной дуги. В последней статье было установлено, что длину дуги $ s $ можно определить, умножив угол в радианах на радиус окружности, $ s = \ alpha r $. Следовательно, линейная скорость $ v $ может быть определена следующим образом:
\ [v = \ frac {s} {t} \]
Возвращаясь к примеру с ветряной турбиной, предположим, что длина лопасти составляет $ 116 \ \ text {ft} $, длина лопастей для обычных ветряных турбин.
Линейная скорость ветряной турбины
Поскольку длина лезвия также равна радиусу, окружность круга, созданного вращением лезвия, может быть определена как $ 2 \ pi (116) \ \ text {ft} = 232 \ pi \ \ text {ft} $.Используя эту информацию, можно создать уравнение для определения линейной скорости.
\ [v = \ frac {20 \ \ text {rev}} {1 \ \ text {min}} = \ frac {20 \ \ cancel {\ text {rev}}} {1 \ \ text {min}} * \ frac {232 \ pi \ \ text {ft}} {1 \ \ cancel {\ text {rev}}} = \ frac {4640 \ pi \ \ text {ft}} {1 \ \ text {min}} \ примерно 14576,99 \ \ text {фут / мин} \]
Взаимосвязь линейной / угловой скорости
Один из самых интересных аспектов математики — это то, как концепции взаимодействуют друг с другом. До сих пор в этой статье угловая скорость определялась как $ \ omega = \ frac {\ alpha} {t} $, где $ \ alpha $ — угол, а линейная скорость — как $ v = \ frac {s} {t} $, где $ s $ — длина дуги.Объедините это с определением длины дуги $ s = \ alpha r $, и получится соотношение:
\ [v = \ frac {s} {t} = \ frac {\ alpha r} {t} = r * \ frac {\ alpha} {t} = r \ omega \]
Нарушая вышесказанное, начнем с линейной скорости $ v $ как $ \ frac {s} {t} $. Затем замените $ s $, длину дуги, на ее определение $ \ alpha r $. Этот шаг дает угловую скорость $ \ frac {\ alpha} {t} $, умноженную на $ r $, радиус. Упрощение угловой скорости дает уравнение для линейной скорости через угловую скорость:
\ [v = r \ omega \]
В примере с ветряной турбиной угловая скорость была определена как $ \ frac {40 \ pi \ \ text {rad}} {1 \ \ text {min}} $ с радиусом $ r = 116 \ \ text {ft} $.Используйте приведенную выше формулу линейной скорости в терминах угловой скорости и сравните результаты с ранее найденной линейной скоростью:
\ [v = \ frac {40 \ pi \ \ text {rad}} {1 \ \ text {min}} * 116 \ \ text {ft} = \ frac {4640 \ pi \ \ text {ft}} {1 \ \ min} \ приблизительно 14576,99 \ \ text {фут / мин} \]
Результирующая линейная скорость такая же, как если бы она была получена из отношения к окружности ограничивающего круга. Также обратите внимание на то, что радианам кажется, что они «исчезают», потому что радианы — это просто действительное число.
Заключение
В этой статье определяется угловая скорость, $ \ frac {\ text {angle}} {\ text {time}} $, и линейная скорость, $ \ frac {\ text {arc length}} {\ text {time}} $. Он также представляет собой реальный пример, показывающий, где эти типы скорости можно найти в повседневной жизни, а также как их использовать. А пока в следующей статье этой серии будут определены тригономические функции!
Как рассчитать угловую скорость
Обновлено 15 декабря 2020 г.
Кевин Бек
В повседневном дискурсе «скорость» и «скорость» часто используются как синонимы.Однако в физике эти термины имеют особые и различные значения. «Скорость» — это скорость перемещения объекта в пространстве, и она задается только числом с определенными единицами измерения (часто в метрах в секунду или милях в час). С другой стороны, скорость — это скорость, связанная с направлением. Таким образом, скорость называется скалярной величиной, тогда как скорость — векторной величиной.
Когда машина мчится по шоссе или по воздуху проносится бейсбольный мяч, скорость этих объектов измеряется относительно земли, тогда как скорость включает больше информации.Например, если вы едете в машине со скоростью 70 миль в час по межштатной автомагистрали 95 на восточном побережье Соединенных Штатов, также полезно знать, идет ли она на северо-восток в сторону Бостона или на юг в сторону Флориды. В случае с бейсбольным мячом вы можете захотеть узнать, изменяется ли его координата y быстрее, чем координата x (летающий мяч), или верно ли обратное (линейный привод). Но как насчет вращения шин или вращения (вращения) бейсбольного мяча, когда машина и мяч движутся к своему конечному пункту назначения? Для такого рода вопросов физика предлагает концепцию угловой скорости .
Основы движения
Вещи перемещаются в трехмерном физическом пространстве двумя основными способами: перемещением и вращением. Трансляция — это перемещение всего объекта из одного места в другое, как при движении автомобиля из Нью-Йорка в Лос-Анджелес. С другой стороны, вращение — это циклическое движение объекта вокруг фиксированной точки. Многие объекты, такие как бейсбольный мяч в приведенном выше примере, демонстрируют оба типа движения одновременно; когда летающий мяч перемещается по воздуху от домашней пластины к дальнему забору, он также вращается с заданной скоростью вокруг своего собственного центра.
Описание этих двух видов движения рассматривается как отдельные физические задачи; то есть, при расчете расстояния, которое мяч проходит по воздуху, на основе таких вещей, как начальный угол запуска и скорость, с которой он покидает летучую мышь, вы можете игнорировать его вращение, а при вычислении его вращения вы можете рассматривать его как сидящего в одном место для настоящих целей.
Уравнение угловой скорости
Во-первых, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-то другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругу или их части.Вы можете вспомнить из геометрии или тригонометрии, что длина окружности равна его диаметру, умноженному на константу пи, или πd . (Значение пи составляет около 3,14159.) Это чаще всего выражается в терминах радиуса круга r , который составляет половину диаметра, что составляет длину окружности 2πr .
Кроме того, вы, вероятно, где-то по пути узнали, что круг состоит из 360 градусов (360 °). Если вы переместитесь на расстояние S по окружности, то угловое смещение θ будет равно S / r.o
В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно в секунду.
Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r от центра круга, причем направление v всегда перпендикулярно к радиус круга, то угловая скорость может быть записана в виде
\ omega = \ frac {v} {r}
, где ω — греческая буква омега.Единицы угловой скорости — радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v / r дает м / с, деленные на m, или с -1 , что означает, что радианы технически являются безразмерной величиной.
Уравнения вращательного движения
Формула углового ускорения выводится таким же существенным образом, как и формула угловой скорости: это просто линейное ускорение в направлении, перпендикулярном радиусу окружности (эквивалентно его ускорению по касательной к круговой траектории в любой точке) делится на радиус круга или части круга, который равен:
\ alpha = \ frac {\ omega} {t}
, потому что для кругового движения:
a_t = \ frac {\ omega r} {t} = \ frac {v} {t}
α , как вы, наверное, знаете, это греческая буква «альфа».2} {r}
Это ускорение направлено в сторону точки, вокруг которой вращается рассматриваемый объект. Это может показаться странным, поскольку объект не приближается к этой центральной точке, так как радиус r фиксирован. Думайте о центростремительном ускорении как о свободном падении, при котором нет опасности столкновения объекта с землей, потому что сила, притягивающая объект к нему (обычно сила тяжести), точно компенсируется тангенциальным (линейным) ускорением, описываемым первым уравнением в эта секция.Если бы a c не было равно a t , объект либо улетел бы в космос, либо вскоре врезался бы в середину круга.
Связанные величины и выражения
Хотя угловая скорость обычно выражается, как уже отмечалось, в радианах в секунду, могут быть случаи, в которых предпочтительнее или необходимо использовать вместо этого градусы в секунду или, наоборот, преобразовывать из градусов в радианы до решения проблемы.
Допустим, вам сказали, что источник света вращается на 90 ° каждую секунду с постоянной скоростью. Какова его угловая скорость в радианах?
Сначала запомните, что 2π радиан = 360 °, и установите пропорцию:
\ frac {360} {2 \ pi} = \ frac {90} {\ omega} \ подразумевает 360 \ omega = 180 \ pi \ подразумевает \ omega = \ frac {\ pi} {2}
Ответ — половина пи радиан в секунду.
Если бы вам дополнительно сказали, что световой луч имеет дальность действия 10 метров, какова будет вершина линейной скорости луча v , его угловое ускорение α и его центростремительное ускорение a с ?
Чтобы решить для v сверху, v = ωr, где ω = π / 2 и r = 10m:
\ frac {\ pi} {2} 10 = 15.2
Зависимость угловой скорости от линейной
Основываясь на предыдущей задаче, представьте себя на очень большой карусели с маловероятным радиусом 10 километров (10 000 метров). Эта карусель совершает один полный оборот каждые 1 минуту 40 секунд или каждые 100 секунд.
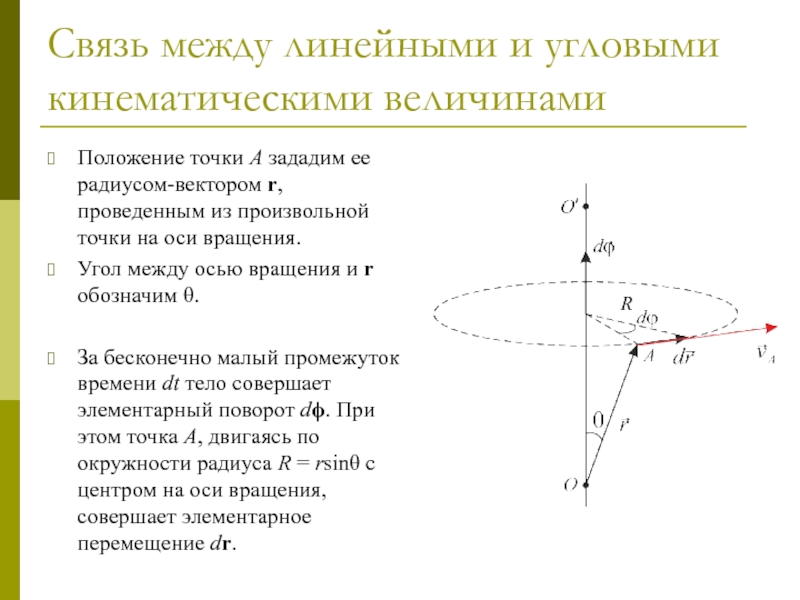
 момент.
момент.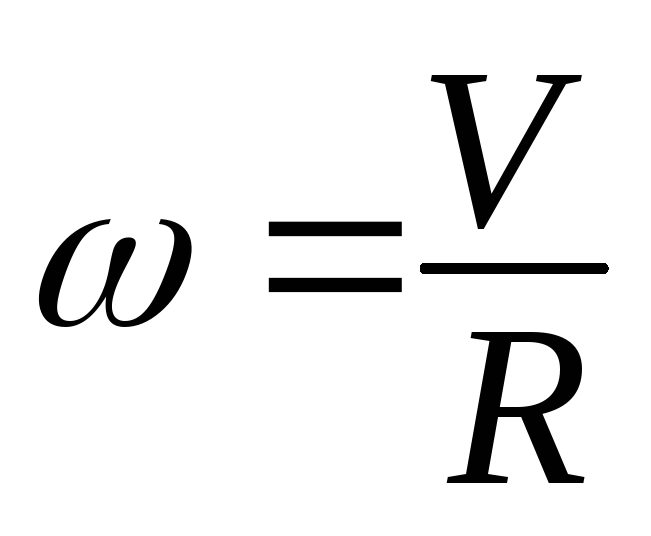
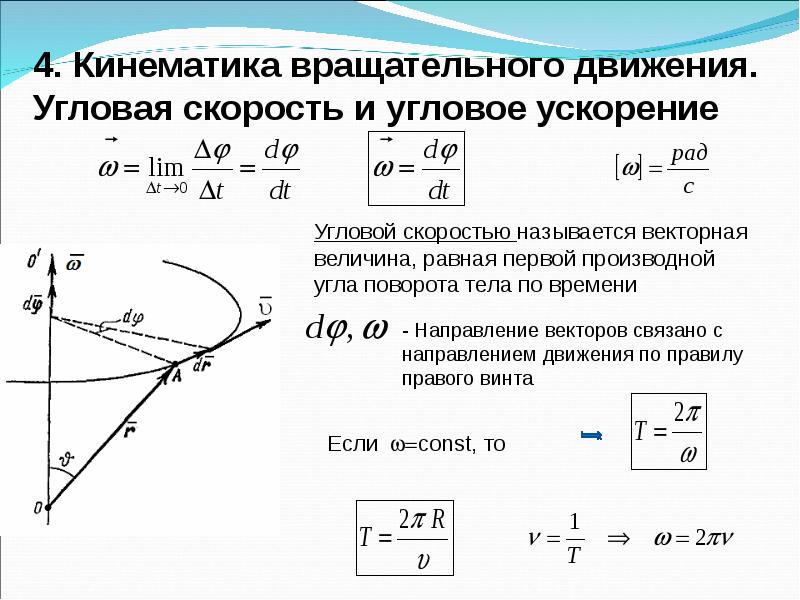
 Кирикстр. 42 средний уровень № 3,6, стр. 42 достаточный уровень №1,2, 3
Кирикстр. 42 средний уровень № 3,6, стр. 42 достаточный уровень №1,2, 3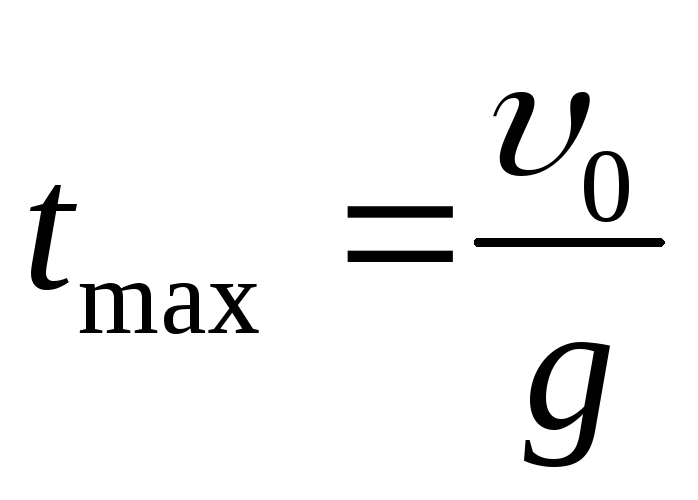 Формирование умения работать в команде. Контроль усвоения знаний и умений учащихся.
Формирование умения работать в команде. Контроль усвоения знаний и умений учащихся.


 Средняя величина угловой скорости w предмета, движущегося от угла q1 до угла q2 за время t выражается как (q2-q1)w)/t. Мгновенной угловой скоростью называют величину, к которой приближается , когда t стремится к нулю. Направление, в котором определяют угловую скорость предмета, перпендикулярно плоскости его движения. Линейная скорость v предмета, находящегося на расстоянии r от фиксированной точки, прямо пропорциональна его угловой скорости: v=rw.
Средняя величина угловой скорости w предмета, движущегося от угла q1 до угла q2 за время t выражается как (q2-q1)w)/t. Мгновенной угловой скоростью называют величину, к которой приближается , когда t стремится к нулю. Направление, в котором определяют угловую скорость предмета, перпендикулярно плоскости его движения. Линейная скорость v предмета, находящегося на расстоянии r от фиксированной точки, прямо пропорциональна его угловой скорости: v=rw.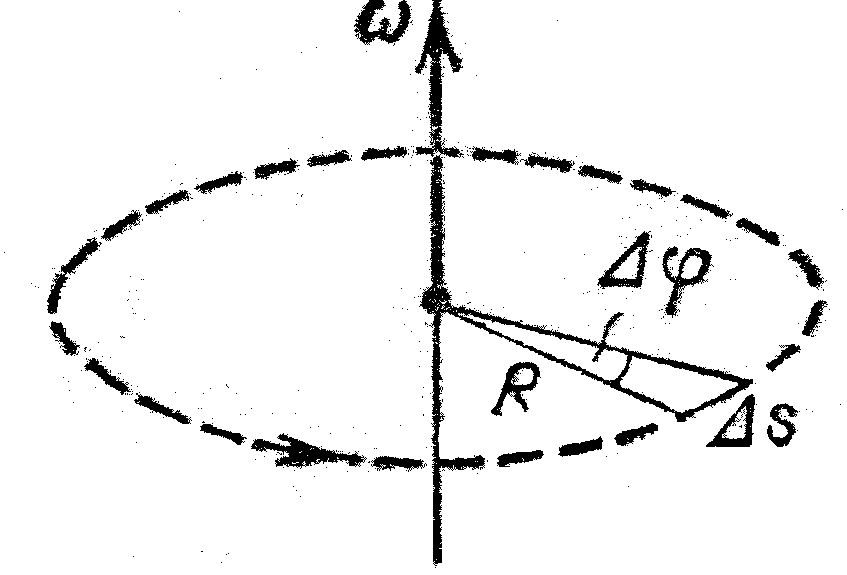 При равномерном вращении тела вокруг неподвижной оси численно его У. с. w=Dj/Dt, где Dj приращение угла поворота j за промежуток времени Dt, а в общем случае w=dj/dt. Вектор У.… … Физическая энциклопедия
При равномерном вращении тела вокруг неподвижной оси численно его У. с. w=Dj/Dt, где Dj приращение угла поворота j за промежуток времени Dt, а в общем случае w=dj/dt. Вектор У.… … Физическая энциклопедия При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости ω = Δφ/Δt, где Δφ приращение угла поворота за промежуток времени Δt. * * * УГЛОВАЯ … Энциклопедический словарь
При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости ω = Δφ/Δt, где Δφ приращение угла поворота за промежуток времени Δt. * * * УГЛОВАЯ … Энциклопедический словарь угловая скорость, f pranc. vitesse angulaire, f … Fizikos terminų žodynas
угловая скорость, f pranc. vitesse angulaire, f … Fizikos terminų žodynas