Как избавиться от эффекта биения колес — видео — журнал За рулем

LADA

УАЗ

Kia

Hyundai

Renault

Toyota

Volkswagen

Skoda

Nissan

ГАЗ

BMW

Mercedes-Benz

Mitsubishi

Mazda

Ford

Все марки

Часто даже отбалансированные колеса являются источником неприятных вибраций при движении. Такое происходит, если диаметр центрального отверстия колесного диска больше, чем диаметр посадочного пояска на ступице. Пластиковые центрирующие кольца-проставки помогут избавиться от ненужного зазора. ЗР протестировал одно из таких изделий.

Проблема несоответствия

Новые колесные диски точно освежат внешний вид машины, неправильно подобранные или установленные — заставят поволноваться, вызвав биение колес. Если вы уверены, что покрышки не деформированы, диски ровные и на шиномонтаже колеса были правильно собраны и отбалансированы, значит, проблема в неточной посадке дисков.

Подбирая диски, всегда обращайте внимание на диаметр их центрального отверстия: в идеале он должен совпадать с диаметром посадочного пояска на ступице. Если центральное отверстие меньше, установить диски просто не получится, если больше — для установки понадобятся центровочные кольца, или проставки.

Сила колец

Материалы по теме

А что, если поставить колеса побольше? — экспертиза ЗР

Сегодня можно найти проставки разных размеров, под любые модификации дисков. Самые простые — пластиковые. Но их изготавливают также и из различных сплавов на основе алюминия (из силумина или дюраля). Несмотря на то, что нагрузка на центровочные кольца небольшая, они рано или поздно изнашиваются или деформируются, а значит их необходимо периодически менять.

Ездить без проставок, если диаметры отверстия в диске и посадочного пояска на ступице не совпадают, нельзя. Иначе неправильная установка колесного диска даст большую нагрузку на подвеску и может привести к серьезным поломкам, вплоть до разрушения отдельных деталей подвески.

Смотри в оба

Предлагаем один раз все увидеть.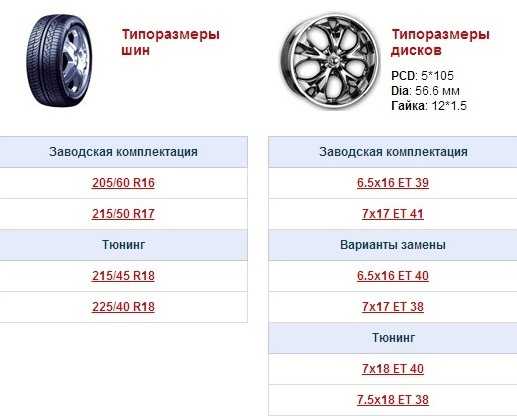 Сначала покажем, когда центровочное кольцо не нужно. Ставим диск на ступицу и смотрим, как он плотно садится: диаметр ступицы соответствует центральному отверстию диска, зазор между ними практически отсутствует.

А теперь смотрите, что произойдет, когда мы установим на ступицу диск, центральное отверстие которого больше ее диаметра. Между посадочным пояском и отверстием в диске есть зазор, и довольно большой. Именно это становится причиной неправильной установки диска и вызывает биение. Значит, здесь не обойтись без проставки.

• Как разбортировать колесо своими руками, показано тут.

Все вопросы и предложения по серии выпусков «Техническая среда» присылайте на [email protected].

Другие выпуски «Технической среды» доступны в нашем спецпроекте, а также на нашем канале в YouTube.

Фото: depositphotos.com

Наше новое видео

Москвич 3: все подробности и первый тест!

2 российские новинки, которые заменят Ford

Что лучше на бездорожье: Лада Веста Кросс или УАЗ Патриот?

Понравилась заметка? Подпишись и будешь всегда в курсе!

За рулем в Дзен

Новости smi2. ru

Что если центральное отверстие на диске больше?

Если центральное отверстие меньше, установить диски просто не получится, если больше — для установки понадобятся центровочные кольца, или проставки.

Если цо большое ставим спокойно диск и радуемся. Подгон цо, кольца, нужны только на авто с болтами для облегчения процедуры монтажа колеса. … Диск центруется и держится на ступице ТОЛЬКО за счет конусов болтов /гаек. Чтобы работало, как вы все хотите, нужно чтобы цо диска было притерто к цо ступицы как плунжер.

Поскольку у штатного оригинального диска центральное отверстие обычно совпадает по диаметру с выступающей частью ступицы, многие думают, что равенство этих диаметров — обязательный и необходимый фактор. Но это не так! Центральное отверстие и его диаметр не играют совершенно никакой роли в центровке и фиксации колеса.

DIA (ЦО в мм) – диаметр центрального отверстия диска. Он должен соответствовать диаметру центрирующего выступа на ступице автомобиля. Допускается отклонение его величины в большую сторону.

В том числе это происходит за счет того, что при изменении вылета колес машина перестает попадать в стандартную накатанную колею, повышаются риски вылета на скорости. Если проставка не достаточно точно отцентрирована – в этом случае возникают эксцентриситеты, нарушающие баланс автомобиля при движении.

Увеличение центрального отверстия на дисках вполне допустимо, но с одним условием – если вы нашли адаптер нужного размера. Что это такое? Это вкладыш – центровочное кольцо из металла или пластика, внешний диаметр которого соответствует отверстию на диске, а внутренний ступичному диаметру.

1) Если диски на вашем авто крепятся болтами, причем отверстий к примеру 5. Как к примеру на Мерседесе, Ауди или Фольксвагене (5-112), на BMW (5-120), ну и при этом неродное центральное отверстие диска (далее ЦО).

Чем больше вылет тем более колесо утапливается во внутрь. … Допускается уменьшение вылета до 5-7 мм, например установка дисков с вылетом 40-42 не приведет ни к каким последствиям, однако большее уменьшение вылета чревато тем что вылезшие колеса начнут задевать за крылья автомобиля.

Увеличение вылета приводит к смещению колеса внутрь арки. В результате диск может упереться в тормозной суппорт или детали подвески, и колесо просто не встанет на место.

Вылетом называется расстояние между срединной плоскостью колеса и поверхностью, которой колесный диск примыкает к ступице. … Именно поэтому, если мы поставим колеса с большим вылетом, колеса расположатся ближе к продольной оси автомобиля. Колея машины при этом уменьшится.

Это расстояние между привалочной плоскостью колесного диска (плоскость, которой прижимается диск к ступице) и осью симметрии диска (CL). Вылет (ЕТ) измеряется в миллиметрах.

DIA – это размер центрального отверстия (ЦО) колёсного диска. Несмотря на кажущуюся простоту, от размера этого параметра многое зависит. Диаметр ЦО на различных марках авто может отличаться, так как автомобиль проектируется под определённые эксплуатационные характеристики.

DIA — диаметр центрального отверстия литого диска (измеряется в миллиметрах). Он должен соответствовать диаметру центрирующего выступа на ступице автомобиля. … Кольцо служит для центрирования на ступице при установке диска.

Проставки и нестандартные колёса значительно изменяют характер управления автомобилем и почти всегда в негативную сторону. Также подобный тюнинг гарантированно приведёт к снижению ресурса подвески. Происходит это из-за перераспределения нагрузок, а также по причине использования тяжёлых нештатных колёс.

Проставки незаменимы для многих отечественных полноприводных автомобилей, так как позволяют устанавливать более широкие диски и, соответственно, резину — пятно контакта возрастает, машина увереннее чувствует себя в грязи. …

Что же дают нам проставки? Они позволяют устранить проблему задевания элементов подвески или тормозной системы. Такая ситуация может возникнуть при замене дисков, резины или тормозных суппортов. Проставки-адаптеры дают возможность установить диски с другой сверловкой или сменить тип крепления колес.

Концентрация напряжений в отверстиях

Введение

История анализа концентраций напряжений начинается в 1898 г.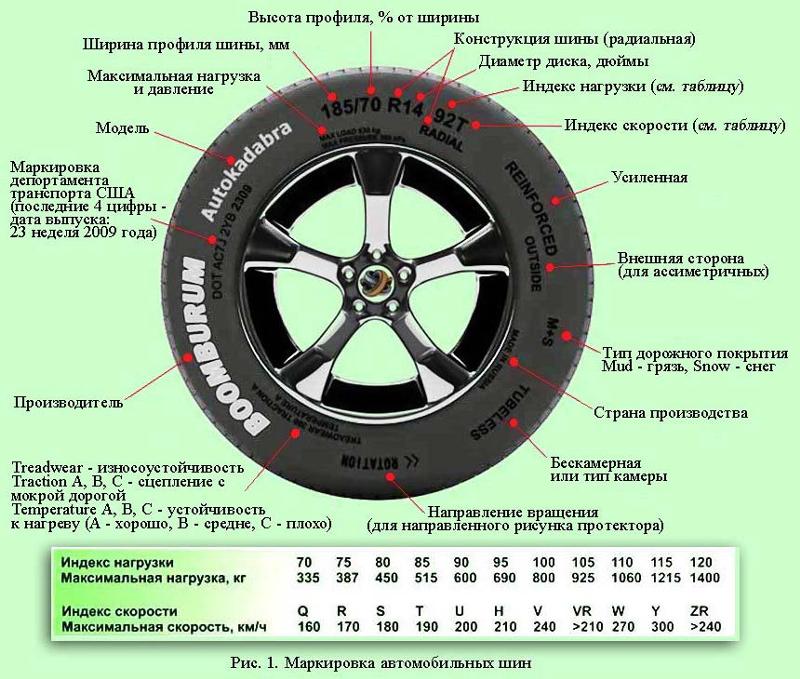 с
Эрнст Густав Кирш
линейно-упругое решение для напряжений вокруг отверстия в бесконечной пластине [1].
Решение Кирша содержит хорошо известную концентрацию напряжения с коэффициентом три.
в отверстии при одноосной нагрузке. Но это еще не все.
Концентрация напряжения может фактически варьироваться от двух до четырех для более сложных
условия нагружения, т. е. напряжённые состояния, отличные от одноосного растяжения.

Начнем с рассмотрения решения Кирша для базового случая одноосного растяжения.
а затем использовать методы суперпозиции для разработки решений для более сложных случаев.
равнодвухосного растяжения и сдвига. Далее следует решение
для общей 2-D нагрузки. И страница заканчивается концентрацией стресса
в плитах конечной ширины.

Одноосное растяжение — решение Кирша (1898)

Решение Кирша для напряжений в отверстии для случая одноосного растяжения
в бесконечной пластине. Одноосное растяжение представлено дистанционным напряжением,
\(\сигма_\infty\).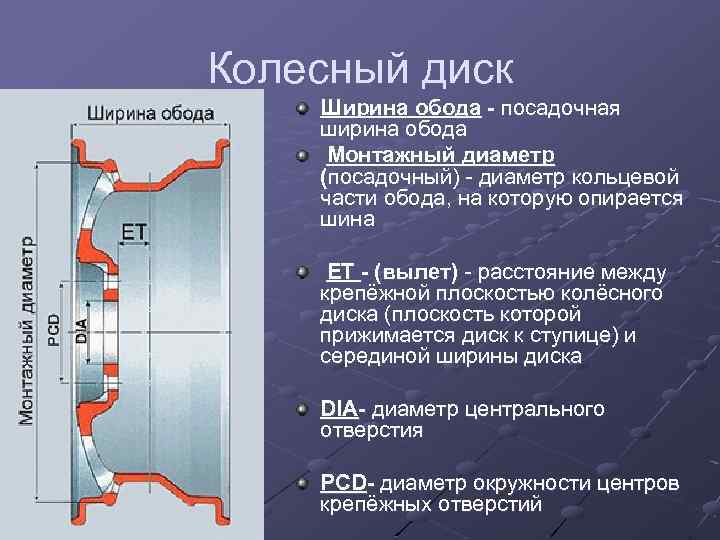 \circ\), а
\(\sigma_{\theta\theta} = \sigma_\infty\), когда \(\theta = \pm \, 9\circ\), как и должно быть.
Касательное напряжение, \(\tau_{r \theta}\), является просто результатом преобразования координат
на \(\sigma_\infty\).

У дыры

При \(r = a\) все члены \(a / r\) равны единице, что дает

\[
\begin{выравнивание}
\sigma_{rr} & = & 0 \\
\\
\sigma_{\theta \theta} & = & \sigma_\infty ( 1 — 2 \cos 2\theta ) \\
\\
\ тау_ {г \ тета} & = & 0
\end{эквнаррай}
\]

Радиальное напряжение, \(\sigma_{rr}\), и напряжение сдвига, \(\tau_{r \theta}\),
нулевые в отверстии, потому что это свободная поверхность.
9\круг\)
что \ (\ sigma _ {\ theta \ theta} = 3 \, \ sigma_ \ infty \) и фактор трех
возникает коэффициент стресса. Это отношение называется коэффициентом концентрации напряжения и
обсуждается ниже.

Это наибольшее напряжение в отверстии, поэтому
первое значение для сравнения с пределом текучести материала для проверки текучести.
Напряженное состояние является одноосным, поэтому значение \(\sigma_{\theta \theta}\) также
эффективное напряжение или напряжение фон Мизеса, которое можно непосредственно сравнить с напряжением материала.
предел текучести.

Обратите внимание, что компоненты напряжения в отверстии не зависят от размера самого отверстия.
Это связано с тем, что пластина бесконечно велика, поэтому размер отверстия
не имеет значения по отношению к пластине.

Коэффициент концентрации напряжений, \(K_t\)

Коэффициент концентрации напряжения , \(K_t\), представляет собой отношение
максимальное напряжение в отверстии, галтели или надрезе (но не в трещине) до
удаленный стресс. Для нашего случая отверстия в бесконечной пластине
\(К_т = 3.\)

Не путайте Коэффициент концентрации напряжения с
Коэффициент интенсивности напряжения , используемый при анализе трещин.
два совершенно разные. Для начала, концентрация стресса
Фактор является безразмерным, а коэффициент интенсивности напряжения — нет.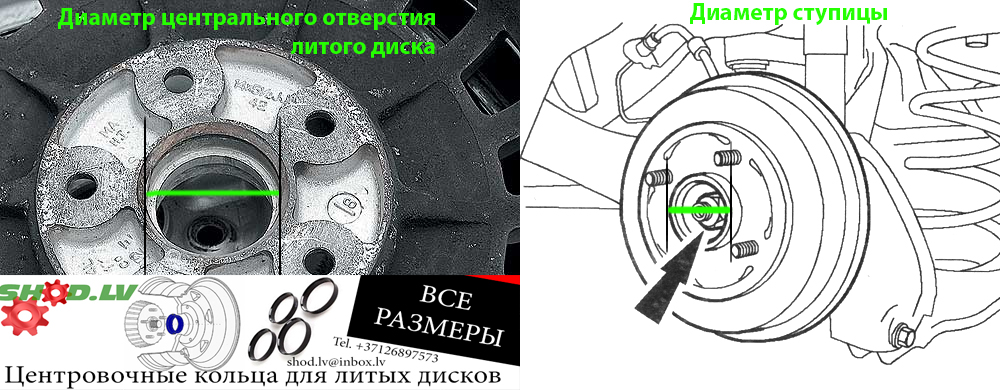
Факторы интенсивности стресса будут обсуждаться на последующих страницах.

Имейте в виду, что все здесь относится к пустой дыре. Не
путайте эту ситуацию с отверстием, содержащим застежку.
Этот сценарий имеет бесконечное множество вариаций в зависимости от
относительные нагрузки, воспринимаемые застежкой и пластиной (с отверстием).
9\circ\) как функция \(r\). Он показывает фактор трех
концентрации на краю отверстия и как она быстро рассеивается с увеличением \(r\).
Концентрация напряжений снова мала на расстоянии одного диаметра от края отверстия,
и действительно пренебрежимо мал на расстоянии двух диаметров.
При анализе методом конечных элементов этот крутой градиент требует очень мелкой сетки в
радиальном направлении для точного моделирования поля напряжений и деформаций.

Комплексное поле напряжений вокруг отверстия показано на рисунке ниже.
Он показывает серию напряженных состояний на краю отверстия, на расстоянии одного радиуса,
и на расстоянии одного диаметра. Нормальные напряжения симметричны слева и справа,
таким образом, условия с обеих сторон применимы и к другой. Это отражено
в уравнениях тем, что \(\cos(2\theta) = \cos(-2\theta)\).
Касательные напряжения с одной стороны отрицательны по отношению к другой, т.
отражается \(\sin(2\theta) = -\sin(-2\theta)\).
9\circ\) выровнены с внешним
одноосная нагрузка , \(\sigma_\infty\). Итак, система координат
прямоугольные, а компоненты напряжения равны \(\sigma_{xx}, \sigma_{yy},\) и
\(\sigma_{xy}\).

Приведенный ниже рисунок касается размера отверстия и его (отсутствия) влияния на
напряжения вокруг него. Противоречивый интуитивный результат состоит в том, что стресс с коэффициентом 3
концентрация не зависит от размера отверстия. Очень маленькое отверстие создает такое же напряжение
концентрация как очень большое отверстие (в бесконечной пластине).

Красные кривые качественно показывают поток силы вокруг
отверстие подобно линиям тока в поле потока жидкости. Расстояние
между кривыми, который является минимумом по бокам отверстия, отражает концентрации напряжений.

Продолжая аналогию с полем течения… высота отверстия
обеспечивает раннее предупреждение силового поля о том, что оно должно отклониться
дыра. Поток должен больше отклоняться для более широкой дыры, но тогда и более широкая дыра тоже
выше, поэтому он предупреждает поток раньше. Конечным результатом является то, что концентрация напряжения
у отверстия всегда три, независимо от размера отверстия.

Это актуально из-за контраста с эллипсами и трещинами. Считают, что
трещина не имеет высоты, чтобы заранее предупредить гипотетическое поле течения, которое
он должен отклоняться. Тем не менее, чем длиннее трещина, тем больше должен отклоняться поток.
следовательно, больше концентрация напряжения. Это будет рассмотрено
более строго на следующих веб-страницах.

Равноосная нагрузка

Равноосная нагрузка состоит из одинакового напряжения как в \(x\), так и в \(y\)
направления. Влияние на напряженное состояние в отверстии
можно определить с помощью суперпозиции решения Кирша, что допустимо
потому что он линейный. Это показано на рисунке ниже. Это показывает, что
концентрация напряжений в отверстии при равнодвуосной нагрузке в два раза меньше, чем
три, как в одноосном случае. Это относится ко всей окружности
отверстия. Напряженное состояние не зависит от \(\тета\), потому что оно одно и то же.
под всеми углами. Подробности см. в общем обсуждении 2-D загрузки ниже.
аналитическая разработка уравнений здесь.
92 \справа)\\
\\
\ тау_ {г \ тета} & = & 0
\end{эквнаррай}
\]

Сдвиговая нагрузка

Эффекты сдвиговой нагрузки можно определить по суперпозиции ее главных напряжений.
На рисунке ниже показаны два главных напряжения, ориентированных на ± 45°, Первый
один положительный и численно равен величине касательного напряжения. Второй — отрицательный.
В результате сдвиговая нагрузка приводит к увеличению концентрации напряжения в отверстии в четыре раза.

94 \right) \left( \left( {\sigma_{yy} — \sigma_{xx} \over 2} \right) \sin 2\theta + \tau_{xy} \cos 2\theta \right) \\
\end{эквнаррай}
\]

и частный случай кольцевого напряжения на краю отверстия

\[
\sigma_{\theta \theta} |_{r=a} \; = \left( \sigma_{xx} + \sigma_{yy} \right) — 2 \left( \sigma_{xx} — \sigma_{yy} \right) \cos 2\theta — 4 \, \tau_{xy } \sin 2\тета
\]

Эффекты конечной ширины

При работе с плитами конечной ширины необходимо вводить доп.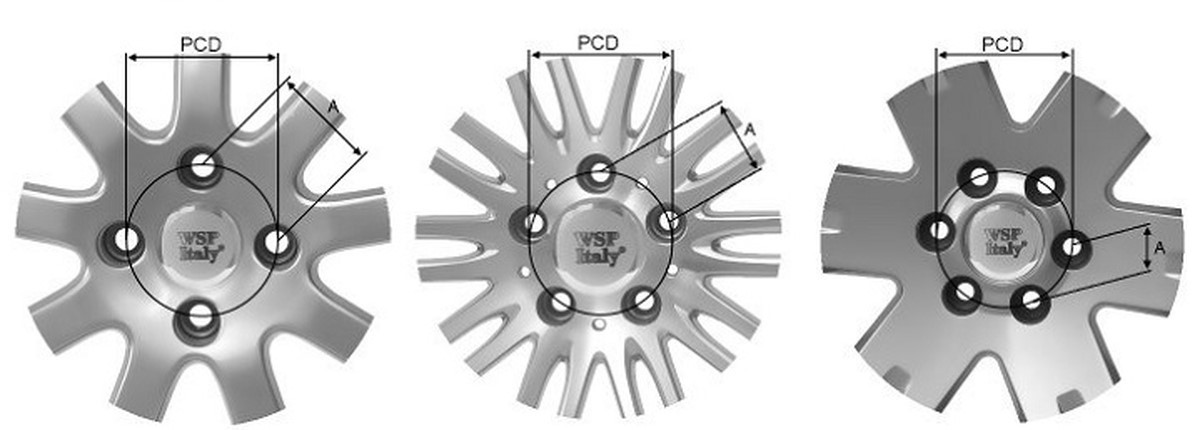
срок, номинальное напряжение, \(\sigma_\text{nom}\). это средний стресс
в отверстии из-за уменьшения поперечного сечения и связано с
\(\sigma_\infty\) по

\[
\text{Принудительно} \; знак равно \sigma_\infty Вт \; знак равно \sigma_\text{nom} ( W — d )
\]

, где \(d\) — диаметр отверстия, \(W\) — ширина пластины, а толщина
игнорируется. Решение для \(\sigma_\text{nom}\) дает

\[
\sigma_\text{nom} = { W \over W — d } \; \сигма_\инфти
\]

Затем коэффициент концентрации напряжения определяется как
9\круг\).
Обратите внимание, что знаменатель здесь НЕ \(\sigma_\infty\),
но вместо этого \(\sigma_\text{nom}\). Это стандартная практика.

Стандартный график зависимости \(K_t\) от безразмерного
Отношение \(d/W\) для пластины показано ниже. \(d/W = 0\) соответствует
бесконечно широкой пластине, и действительно, \(K_t = 3\) в этой точке.
Уравнение кривой, которое на самом деле является эмпирическим, имеет вид

\[
K_t = 3 — 3,14 \left( {d \over W} \right) + 3,667 \left( {d \over W} \right)^2 — 1,527 \left( {d \over W} \right)^3
\]

График показывает, что \(K_t\) уменьшается к 2 по мере того, как \(d/W\) приближается к 1,
и можно было бы заключить, что \(\sigma_\text{max}\) поэтому
также уменьшается. Но это абсолютно неправильно. Причина в том, что
\(K_t\) больше не является отношением \(\sigma_\text{max}\) к \(\sigma_\infty\).
Вместо этого это отношение к \(\sigma_\text{nom}\). Отношение к \(\sigma_\infty\)
получается

\[
{ \sigma_\text{max} \over \sigma_\infty} \; знак равно
\left( { \sigma_\text{max} \over \sigma_\text{nom} } \right) \!
\left( { \sigma_\text{nom} \over \sigma_\infty} \right) \; знак равно K_t \, {W \над W — d}
\]

И последним членом можно манипулировать, чтобы получить

\[
{ \sigma_\text{max} \over \sigma_\infty} \; знак равно
К_т\; {1 \ над 1 — \ влево ( д \ над W \ справа) }
\]

, который позволяет отображать весь член в зависимости от безразмерного параметра \(d / W\).

Обратите внимание, что кривая \(\sigma_\text{max} / \sigma_\infty\) изначально плоская и равна 3
для всех малых значений \(d/W\), но затем начинает резко возрастать с
увеличивая \(d/W\) при больших его значениях. начальный плоскостность кривой при
небольшие значения \(d / W\) можно интерпретировать как \(\sigma_\text{max}\), первоначально остающиеся неизменными
поскольку ширина \(W\) уменьшается от бесконечности до конечных значений.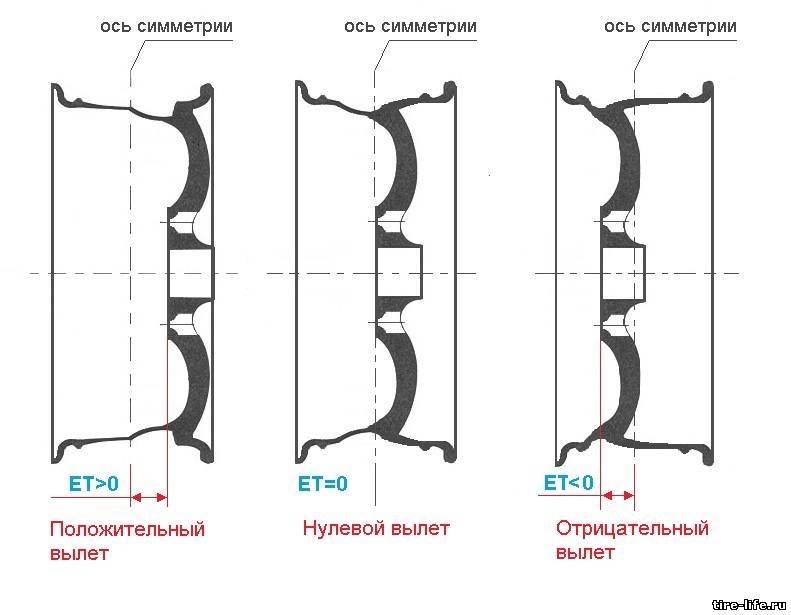 Начальный
уменьшение относительно бесконечности незначительно.

Не менее интересен тот факт, что соотношение \(\sigma_\text{max} / \sigma_\infty\) никогда не
уменьшается. В то время как отношение \(K_t\) по отношению к \(\sigma_\text{nom}\) всегда уменьшается
с увеличением \(d/W\) отношение относительно \(\sigma_\infty\) всегда увеличивается.
Другими словами, увеличение диаметра отверстия или уменьшение ширины пластины в пластина конечной ширины будет
фактически всегда увеличивайте максимальное напряжение в отверстии.

Может ли \(\boldsymbol{\sigma_\text{max}}\) превышать \(\boldsymbol{\sigma_\text{урожайность}}\)?

И последнее, что нужно учитывать… Имейте в виду, что на самом деле
никакое напряжение не может превышать предел текучести материала, \(\sigma_\text{урожайность}\)
(холодная обработка в сторону). Так как же разрешить ситуацию, когда
вычисленное напряжение \(\sigma_\text{max}\) больше, чем \(\sigma_\text{урожайность}\)?

Разрешение состоит в том, что вычисленное значение \(\sigma_\text{max}\) равно
неверно, потому что это результат линейной упругости
расчет. Но на самом деле материал будет поддаваться, оказывая
линейно-упругое решение спорно.

Ссылки

1. Кирш, Э.Г., «Die Theorie der Elastizitt und die Bedrfnisse der Festigkeitslehre», Zeitschrift des Vereines deutscher Ingenieure, Vol. 42, стр. 797-807, 1898.

• http://en.wikipedia.org/wiki/Ernst_Gustav_Kirsch
• http://en.wikipedia.org/wiki/Kirsch_equations

Благодарности

Спасибо Грегу Тодду за вклад в эту страницу.

Истинное положение – Допуск положения

GD&T Символ:

Определение:

Истинное положение, или просто положение, как его называет стандарт ASME Y14.5, определяется как общее допустимое отклонение, которое функция может иметь от ее «истинное» положение. « True Position» — это точная координата или местоположение, определяемое базовыми размерами или другими способами, которые представляют номинальное значение. Другими словами, допуск Геометрических размеров и допусков «Положение» показывает, насколько далеко местоположение вашего объекта может отличаться от его «Истинного положения» .

Позиция — один из самых полезных и сложных символов в GD&T. Два метода использования позиции, обсуждаемые на этой странице, будут RFS или независимо от размера элемента и в зависимости от существенного условия (максимальное материальное состояние или наименьшее существенное состояние). Однако, поскольку это такой полезный символ, мы продолжим добавлять контент и примеры для других применений этого изящного маленького символа в ближайшие месяцы.

Применение:

Хотя это и неверно, мы озаглавили эту страницу и иногда ссылаемся на символ как «Истинное положение», поскольку это обычно термин, на который ссылаются люди, когда ищут допуск положения. Однако в стандарте ASME Y14.5 это правильно называется просто «Позиция». Для ясности в отношении этих двух терминов ознакомьтесь с нашей статьей и видео здесь.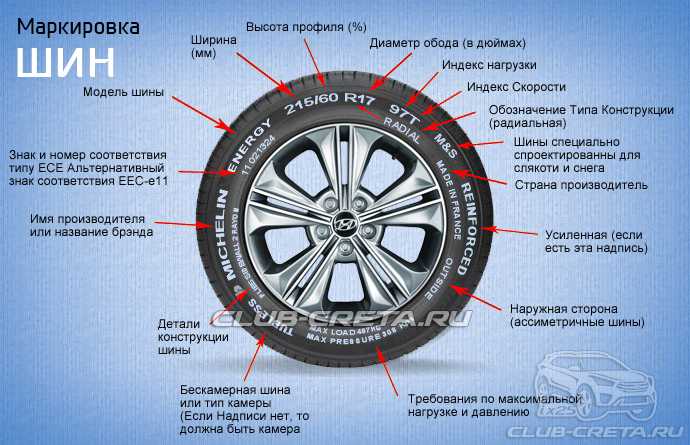

Позиция может быть применена к любому элементу размера (элементу с физическими размерами, например, отверстием, прорезью, бобышкой, выступом или сферой) и управлять центральными элементами этих элементов размера. См. приведенные выше центральные элементы отверстия, прорези и сферы. Расположение поверхностей должно контролироваться через профиль. Положение можно использовать с максимальным условием материала (MMC), минимальным состоянием материала (LMC), проекционными допусками и касательными плоскостями.

На изображении ниже вы можете видеть, как отверстие обозначается с помощью символа допуска положения. Тем не менее, это также может быть применено к любому элементу размера, требующему допуска местоположения, например штифту, бобышке или даже шпоночному пазу. При наличии отверстия в детали, например в массиве болтов, обычно вызывается истинное положение. Его можно использовать практически везде, чтобы 90 176 представляли объекты любого размера.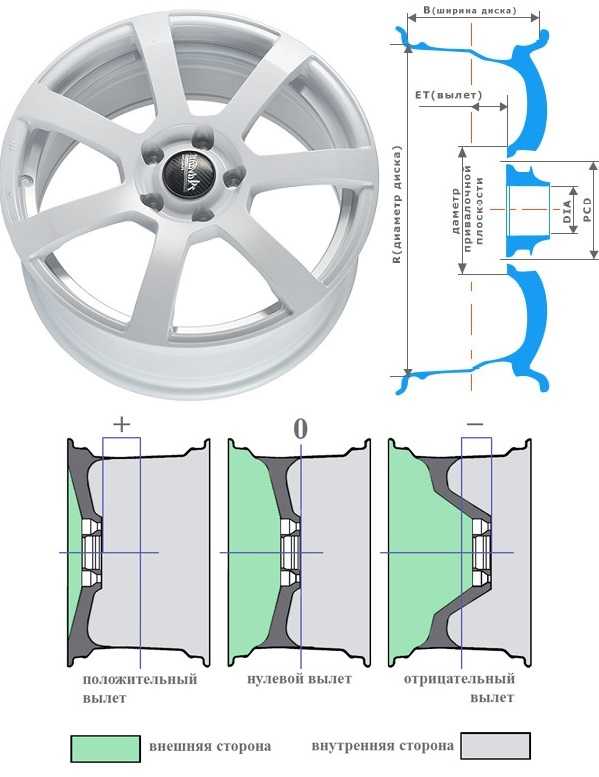

Положение относительно оси, точки или плоскости определяет, насколько объект может отличаться от заданного точного истинного положения. Опять же, True Position — это точное идеальное местоположение функции, расположен и сориентирован на опорную систему отсчета с помощью базовых размеров .

Зона допуска положения

Допуск представляет собой трехмерную зону допуска, окружающую истинное положение. При указании допуска положения базовые элементы ссылаются на фрейм управления элементом. Это означает, что у вас будет точная точка, где положение должно быть  относительно системы отсчета, и ваш допуск определяет, насколько далеко вы можете быть от нее. Положение чаще всего определяется двумя или тремя опорными элементами, чтобы точно определить и сориентировать истинное положение. Если элемент размера является цилиндрическим элементом, таким как отверстие в детали, значению размера в рамке управления элементом предшествует символ диаметра, представляющий круглую или цилиндрическую зону допуска.

Цилиндрическая зона допуска будет проходить через толщину детали, если это отверстие. Вся ось элементов, средняя плоскость или точка должны быть расположены в пределах этой зоны допуска.

Для измерения или проверки элемента, относящегося к управлению положением, можно выполнить измерения по осям X и Y элемента относительно опорных элементов, вызываемых в кадре управления элементом. Эти измерения можно быстро преобразовать в общее диаметральное отклонение. Если ваше диаметральное отклонение меньше указанного допуска, функция проходит. Помните, что для того, чтобы зафиксировать отклонения ориентации, необходимо будет выполнить несколько измерений по «глубине» отверстия или элемента.

В приведенном выше примере измеренное отклонение отверстия составляет 0,003 дюйма по оси X и 0,002 дюйма по оси Y. Используя приведенную формулу, расчетное отклонение диаметра составляет 0,007 дюйма. Заявленный позиционный допуск составляет 0,008 дюйма, поэтому деталь соответствует спецификации и может быть принята.

Положение с использованием модификатора состояния материала (MMC/LMC)

Положение элемента размера с MMC используется, когда функциональный датчик идеально подходит для проверки детали, обычно это используется, когда используется посадка с зазором с некоторыми своего рода застежка.

Если вы задаете элемент управления с помощью MMC, это позволяет допуску местоположения зависеть от размера элемента. Вы увидите положение, называемое MMC, очень часто в шаблонах болтов с зазором, где расположение всех болтов зависит от размера отверстия с зазором. LMC с положением немного менее распространен, но часто используется, когда требуется контролировать минимальную толщину стенки.

Позиция, используемая с максимальным состоянием материала, становится очень полезным элементом управления. Положение в сочетании с допуском размера этого элемента может одновременно управлять положением, ориентацией, формой и размером элемента. Положение MMC полезно для создания функциональных датчиков, которые можно использовать для быстрой вставки в деталь, чтобы увидеть, все ли в пределах спецификации.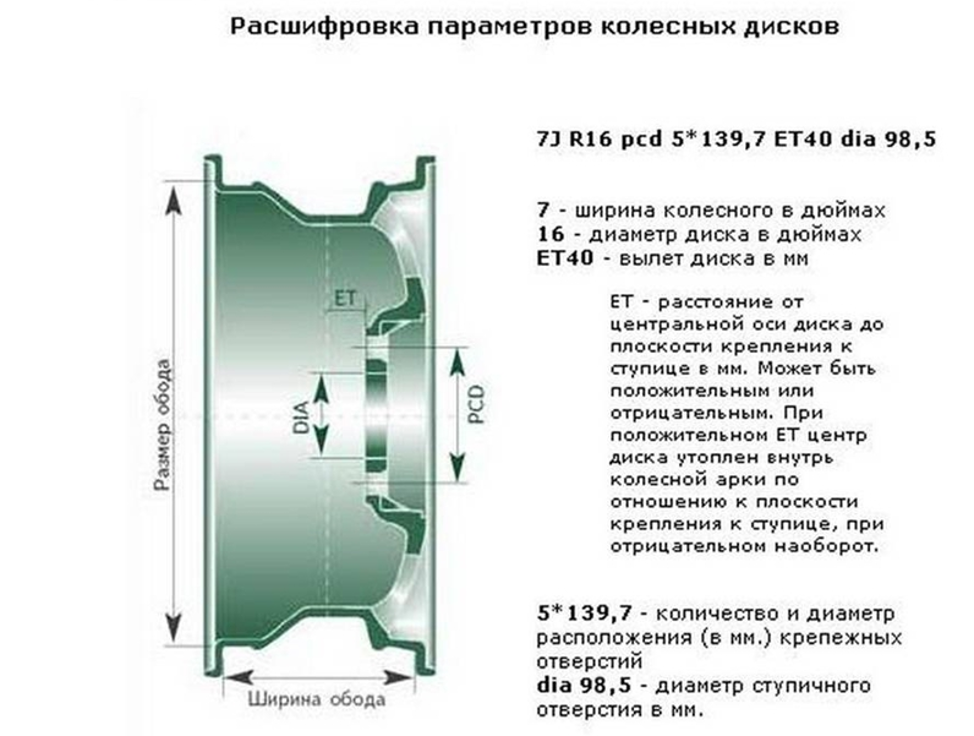 В то время как допуск положения сам по себе определяет, насколько далеко от истинного положения может находиться элемент независимо от размера элемента, position в сочетании с MMC задает минимальный размер и позиционное расположение отверстия для сохранения функционального контроля. Это позволяет позиции детали зависеть от фактического размера элемента. Это достигается путем добавления к детали бонусного допуска. По мере приближения детали к MMC ограничения становятся более жесткими, и отверстие должно быть ближе к ее положению. Но, если отверстие немного больше (но все еще соответствует спецификации), оно может еще больше отклониться от своего истинного положения и по-прежнему обеспечивать правильную работу (например, прохождение болта).

Зона допуска такая же, как и выше, трехмерный цилиндр с центром в истинном положении, на которое ссылаются базовые поверхности. Цилиндрическая зона допуска будет проходить через толщину детали и будет различаться по диаметру в зависимости от допустимого дополнительного допуска по отношению к фактическому размеру элемента.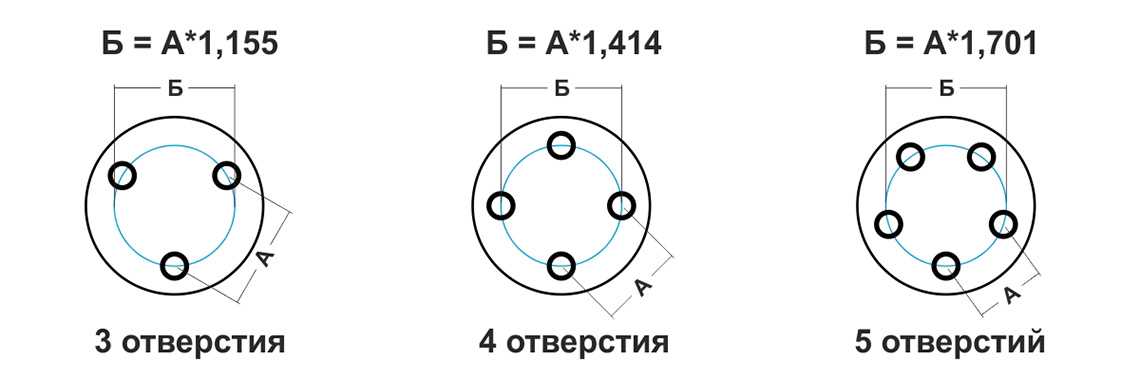

Бонусный раунд

Когда функциональный датчик используется для Позиции, любое отличие фактического размера элемента от максимального состояния материала будет дополнительным допуском. Бонусный допуск для положения затем увеличивается по мере приближения детали к LMC. Цель выноски о максимальном состоянии материала состоит в том, чтобы гарантировать, что, когда деталь находится в наихудших допусках, Позиция и  Размер отверстия/штифта всегда подходит. Например, если у вас был большой размер отверстия, но все еще был в допуске (ближе к LMC), вы увеличиваете бонусный допуск для себя, увеличивая допуск положения. Теперь центр отверстия может больше смещаться из-за дополнительного допуска.

Бонусный допуск = (измеренный размер отверстия – размер отверстия MMC)

Примечание. Имейте в виду, что обратное верно для положительного элемента, такого как штифт, где  меньше  булавка означает, что у вас больше бонусной терпимости.

Когда деталь проверяется на предмет положения под элементом спецификации размера, обычно используется функциональный датчик, чтобы убедиться, что вся область функции находится в пределах спецификации. По сути, это моделирование наихудшего сценария границы сопрягаемых частей. Если у вас есть спецификация для максимального состояния материала, желаемое состояние заключается в том, что поверхность элемента не будет пересекать функциональную оболочку, известную как виртуальное состояние. Для MMC на отверстии это обычно означает границу «наихудшего сценария», при которой сборка еще возможна. Следующие формулы используются для создания датчика положения в MMC.

Фиксированное измерение внутреннего элемента

Для истинного положения под MMC отверстия :

Калибр Ø (штифт) = Мин. Ø отверстия (MMC) — Допуск истинного положения

Фиксированный калибр внешнего элемента

Для положения под MMC штифта :

Калибр Ø (калибр отверстия) = Макс. Ø штифта (MMC) + Допуск истинного положения даны на чертеже в качестве основных размеров. Все элементы датчика должны быть расположены в истинных позициях, но размеры должны соответствовать приведенным выше формулам.

Помните, что чем дальше вы находитесь от MMC, когда на нее ссылаются в рамке управления функцией, тем больше бонусных допусков вам разрешено. Для отверстия, чем больше диаметр (ближе к LMC), тем больше дополнительный допуск для вашего истинного положения.

Вызывается с символом Ø или без него.

Позиция может быть вызвана двумя способами: либо как расстояние, по осям X и Y, либо, чаще всего, как диаметр. Когда положение вызывается как расстояние, вам разрешается отойти от допуска в направлении X или Y на разрешенный допуск. Однако в этом случае зона допуска образует квадрат. Это обычно нежелательно, так как углы квадрата дальше от центра, чем стороны. Это также удалило более 57% вашей зоны толерантности! Чаще всего положение относительно местоположения обозначается символом диаметра (Ø), который называется цилиндрической или круглой зоной допуска.

Запутались? Не волнуйтесь! Для получения более подробной информации о том, как бонусные допуски влияют на эти выноски, см. разделы  Максимальное состояние материала . Или ознакомьтесь с нашим курсом GD&T , где мы подробно рассмотрим символ позиции!

Связь с другими символами GD&T:

Символ положения является позиционным символом для определения геометрических размеров и допусков. Он находит особенности размера, а также контролирует ориентацию. В сочетании с допуском размера этого элемента они управляют размером, местоположением, ориентацией и формой. Однако он не может управлять расположением поверхностей, где вступает в действие профиль поверхности. Он действует так же, как и положение, однако он может управлять расположением, ориентацией и формой элементов поверхности.

Истинное положение управляет ориентацией, что означает, что оно уже управляет элементом так же, как Перпендикулярность, Параллелизм и Угловатость. Допуск как положения, так и этих элементов управления ориентацией относится к цилиндрической оболочке центральной оси. Однако с истинным положением вы можете сделать допуск привязанным к нескольким базам, а не только к одной с перпендикулярностью оси, таким образом, также контролируя местоположение. Когда вы указываете истинное положение с помощью баз на грани и сторонах детали, также контролируется перпендикулярность.

Специальные примечания:

Вот пример урока из нашего курса «Основы GD&T». Мы объясняем, почему гораздо лучше использовать допуск положения и базовые размеры, а не размещать объект с помощью системы координатных размеров.

Позиция, вероятно, является наиболее широко используемым символом в GD&T.