Формула частоты в физике

Формула частоты в физике

Определение

Частота — это физический параметр, которые используют для характеристики периодических процессов.
Частота равна количеству повторений или свершения событий в единицу времени.

Чаще всего в физике частоту обозначают буквой $\nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$

\[\nu =\frac{1}{T}\left(1\right).\]

Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:

\[\nu =\frac{N}{\Delta t}\left(2\right),\]

где $\Delta t$ — время за которое происходят $N$ колебаний. {-1}=Гц.\]

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

\[{\nu =\nu }_1-\ {\nu }_2\left(3\right).\]

Еще одно величиной характеризующей колебательный процесс является циклическая частота (${\omega }_0$), связанная с частотой как:

\[{\omega }_0=2\pi \nu \left(4\right).\]

Циклическая частота измеряется в радианах, деленных на секунду:

\[\left[{\omega }_0\right]=\frac{рад}{с}.\]

Частота колебаний тела, имеющего массу$\ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(5\right). \]

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(6\right),\]

где $g$ — ускорение свободного падения; $\ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(7\right),\]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени.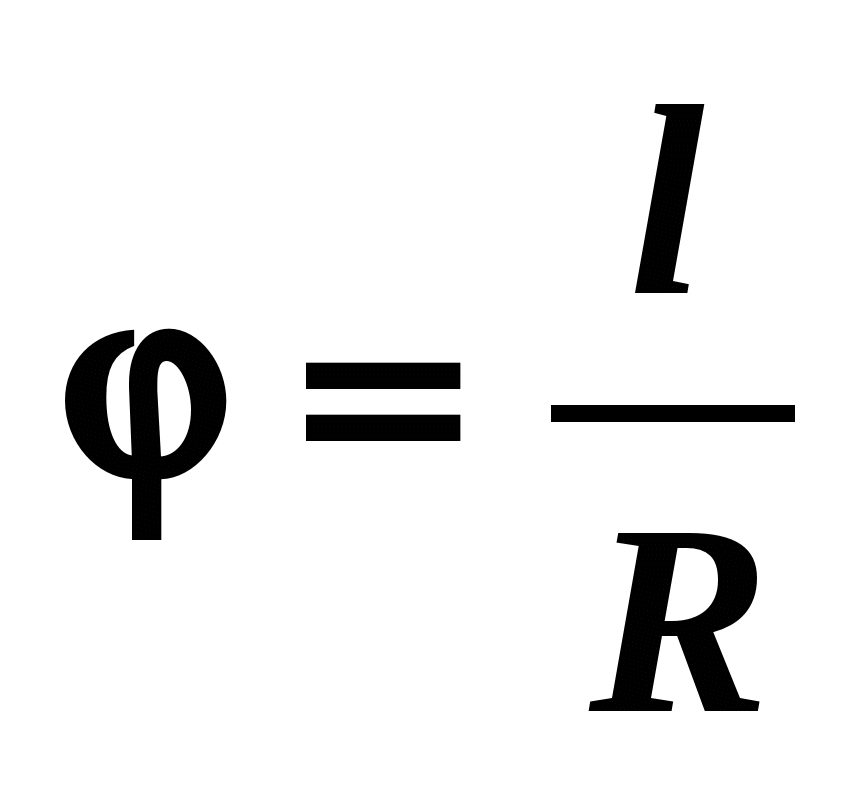 Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(8\right).\]

Единицей измерения частоты дискретных событий является обратная секунда:

\[\left[n\right]=\frac{1}{с}.\]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:

\[n=\frac{1}{\tau }\left(9\right).\]

Примеры задач с решением

Пример 1

Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?

Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.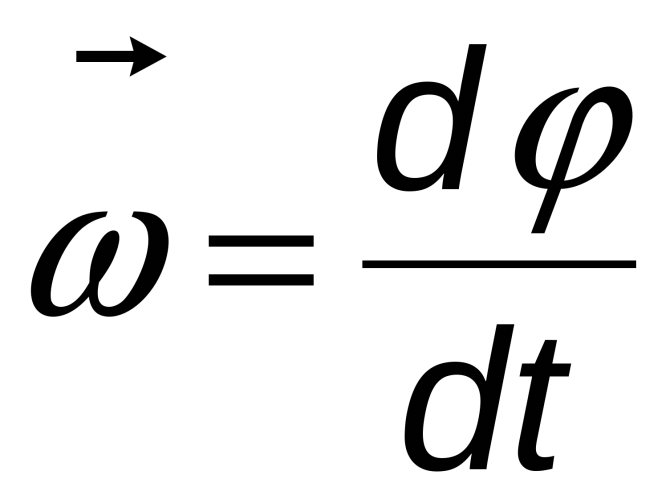

\[\nu =\frac{N}{\Delta t}\left(1.1\right).\]

Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $\Delta t=1\ мин=60\ с$. Вычислим частоту:

\[\nu =\frac{600}{60}=10\ \left(Гц\right).\]

Ответ. $\nu =10Гц$

Пример 2

Задание. На рис.1 изображен график колебаний некоторого параметра $\xi \ (t)$, Какова амплитуда и частота колебаний этой величины?

Решение. Из рис.1 видно, что амплитуда величины $\xi \ \left(t\right)={\xi }_{max}=5\ (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:

\[T=2\ \left(c\right).\]

Частота — величина обратная периоду колебаний, значит:

\[\nu =\frac{1}{T}=0,5\ \left(Гц\right).\]

Ответ. 1) ${\xi }_{max}=5\ (м)$. 2) $\nu =0,5$ Гц

Читать дальше: формулы математического маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

401. Як визначається частота обертання магнітного поля статора, частота обертання ротора? Що таке ковзання?

Обмотка ротора
пересекается магнитным потоком с
частотой

Частота индуктируемой
в роторе ЭДС:

Частота вращения
МДС ротора относительно статора:

Частота
ЄДС и тока зависит от относительной
разности частот вращения поля и
ротора называемой скольжением:

402. При яких умовах можна здобути обертове магнітне поле в ад?

П
ри
включении обмотки статора в сеть
трехфазного тока возникает вращающееся
магнитное поле статора, частота вращения
которого определяется выражением:

В
ращающееся
поле статора (полюсы и ) сцепляются
как с обмоткой статора, так и с обмоткой
ротора и наводит в них ЭДС. ЭДС обмотки
статора, являясь ЭДС самоиндукции,
действует встречно приложенному к
обмотке напряжению и ограничивает
значение тока в обмотке. Обмотка ротора
замкнута, поэтому ЭДС ротора создает в
стержнях обмотки ротора токи. Взаимодействие
этих токов с полем статора создает на
роторе электромагнитные силы направление
которых определяют по правилу «левой
руки». Из рисунка видно, что силы
стремятся повернуть ротор в направлении
вращения магнитного поля статора.
Совокупность сил создает на роторе
электромагнитный момент приводящий
его во вращение с частотой Вращение
ротора посредством вала передается
исполнительному механизму.

Таким образом,
электрическая энергия, поступающая из
сети в обмотку статора, преобразуется
в механическую энергию вращения ротора
двигателя.

403.
Що називається
ковзанням
?

404. У яких режимах може працювати ам?

Двигательній
режим:

405.

У чому схожість і різниця ад та трансформатора ?

При
работе с моделью следует сформировать
чёткое представление о сходстве и
различии процессов в асинхронном
двигателе (АД) и трансформаторе (ТР) при
изменении нагрузки на валу АД. 
Приципиальным
отличием АД от трансформатора (ТР)
является наличие у АД режимов генератора
и тормоза, в которых изменяется направление
потока механической энергии, что
соответствует изменению знака мощности,
рассеиваемой на сопротивлении нарузки
АД R2*(1-s)/s при скольжениях s<0 и s>1,0.
Кроме того, в режиме генератора в АД
изменяется направление потока элекрической
энергии, что возможно только при работе
с отрицательным коэффициентом мощности,
т.е. со смещением фазы тока относительно
напряжения на угол больше 90 градусов.
На векторной диаграмме (ВД) это
приблизительно соответствует переходу
рабочей точки на нижнюю полуокружность
круговой диаграммы тока I1. 
При
значительном сходстве схемы замещения
и ВД АД и ТР следует обратить внимание
на более выраженное влияние нагрузки
на основной магниный поток АД. Это
происходит за счёт падений напряжения
на активном сопротивлении статора R1 и
индуктивном сопротивлении потока
рассеяния X1, снижающих долю ЭДС основного
магитного потока E1 в балансе напряжений
цепи статора. По сравнению с трансформатором
эти сопротивления существенно больше,
соотвественно сильнее выражено и
размагничивающее влияние нагрузки,
т.к. при её увеличении возрастает ток
ротора I2~I1, увеличивается падение
напряжения на Z1=R1+jX1 и снижается ЭДС E1 и
соответствующий ей магнитный поток Ф.
При этом, в отличиче от ТР, в АД невозможно
подмагничивание магнитопровода за счёт
обмена энергией с нагрузкой, т.к. она
имеет чисто активный характер.

Частотный цикл – Вопросы и ответы ​по МРТ

Во избежание наложения частот цифровая выборка МР-сигнала должна выполняться как минимум в два раза быстрее, чем самая высокая ожидаемая частота. Эта критическая частота дискретизации известна как частота Найквиста .  Если частота дискретизации сигнала меньше, чем предел Найквиста, произойдет ошибочное присвоение более высоких частот более низким частотам.

В отличие от наложения в направлении фазового кодирования, наложение в направлении частотного кодирования обычно не является проблемой в современной клинической МРТ. Это связано с тем, что наложение частот в значительной степени устраняется двумя способами: 1) передискретизация сигнала и 2) полосовая фильтрация перед реконструкцией изображения.

Передискретизация означает, что выполняется больше измерений данных МР-сигнала, чем требуется для разрешения изображения. В большинстве современных МР-томографов МР-сигнал записывается 512-1024 раз на эхо (хотя разрешение дисплея в направлении частотного кодирования обычно принимается равным 256). Другими словами, частота дискретизации Найквиста в 2-4 раза превышает самую высокую частоту сигнала. Поскольку эта задача решается простым увеличением скорости оцифровки схемы дискретизации, она практически не требует потери времени и происходит «невидимо».

Двукратный уровень частотной передискретизации выполняется по умолчанию на большинстве МРТ-сканеров, хотя коэффициент передискретизации можно регулировать.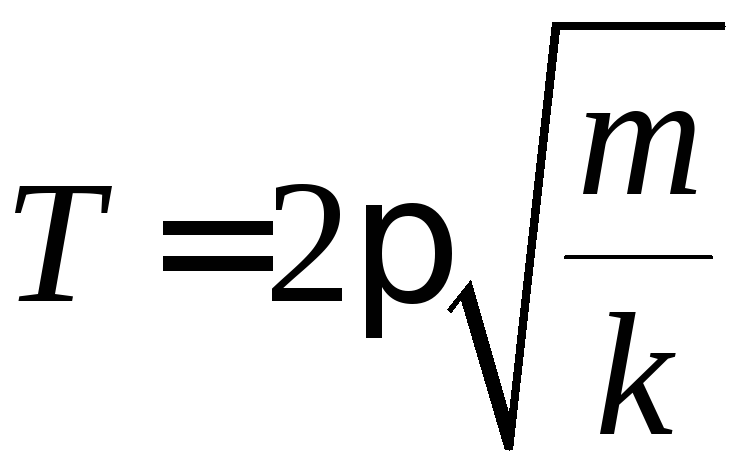 Определенные поставщиками термины для этого метода включают «частотную передискретизацию» (Siemens, Philips, Hitachi), «сглаживание» (GE) и «подавление переноса частоты» (Canon).

Полосовая фильтрация — это аналоговый, цифровой или гибридный метод устранения паразитных высокочастотных составляющих. Фильтр «проходит» через все частотные составляющие в желаемом диапазоне, но ослабляет/отбрасывает частоты за пределами выбранного диапазона.

В результате передискретизации и фильтрации необработанного МР-сигнала перед реконструкцией изображения наложение частот в направлении частотного кодирования практически незаметно в современной МРТ.

Расширенное обсуждение (показать/скрыть)»

Ссылки
     Pusey E, Yoon C, Anselmo ML, Lufkin RB. Псевдонимы артефактов в МРТ. Comput Med Imag Graphics 1988; 12:219-224.

Похожие вопросы
     Что такое псевдоним?

↑ Полный список вопросов ↑

Развертка фазы в непрямом времени пролета

В этой статье мы объясним причину накрутки фазы в камерах глубины с непрямым временем пролета (iToF), ошибку измерения, которую она создает, и различные методы устранения ошибки измерения, чтобы позволяют проводить измерения на больших расстояниях.

Chronoptics разрабатывает модули непрямого измерения глубины по времени полета, уделяя особое внимание созданию наилучшего облака точек для данного приложения. Чтобы получить совет по решению проблемы наложения фазы в вашей Time-of-Flight камере или по разработке более совершенных камер, обращайтесь по адресу [email protected]

. Камеры глубины Indirect Time-of-Flight (iToF) измеряют разность фаз между испускаемым лазерным импульсом. и его отражение. Эта разность фаз кодирует, как далеко прошел свет и, следовательно, как далеко находится объект, а измерение фазы выполняется для каждого пикселя одновременно.

Измерение глубины выполняется путем корреляции отраженного лазерного импульса с эталонным сигналом. Оба этих сигнала представляют собой прямоугольные волны, а коррелированный сигнал представляет собой треугольную волну, как показано ниже.

Рис. 1. Взаимная корреляция двух прямоугольных сигналов представляет собой сигнал треугольной формы. Фаза треугольной формы волны кодирует расстояние, пройденное прямоугольной волной лазерного импульса.

Фаза треугольной волны кодирует пройденное расстояние, где фаза находится в диапазоне от 0 до 2π. Из фазы мы можем рассчитать расстояние, используя приведенное ниже уравнение, где ϕ — фаза, c — скорость света, f — частота модуляции прямоугольной волны.

Фаза нормирована на 2π и умножена на постоянную скорость света, в два раза превышающую частоту модуляции. Дополнительный коэффициент 2 появляется потому, что свет прошел к объекту и обратно, удваивая расстояние, которое мы хотим измерить. Когда фаза равна 2π, максимальное расстояние, которое можно измерить, составляет

Современные датчики изображения iToF, такие как Melexis MLX75027, имеют диапазон частот модуляции 10–100 МГц, что соответствует максимальному расстоянию от 15 до 1,5 м.

Измерение фазы является круговым, что означает, что когда измерение проходит за 2π, измерение возвращается к 0 (это называется свертыванием фазы), потому что измерение перешло к следующему повторению, в нашем случае к следующему треугольному пику на рисунке 1. анимация ниже отображает фактическое расстояние в зависимости от фазы измерения для частоты 40 МГц.

Рис. 2: Влияние наложения фазы на измеренную фазу. Когда пройденное расстояние превышает максимальное расстояние (3,8 м при 40 МГц), измерение фазы возвращается к 0,9.0006 Из-за переноса фазы объект всегда будет измеряться в первом интервале расстояний, называемом интервалом неоднозначности, как показано на рисунке 3. Объект может находиться в любой из скобок неоднозначности, и цель развертывания фазы заключается в том, чтобы выяснить, какая скобка является правильной.

Рис. 3: Графическое представление наложения фаз. Объекты за пределами максимального расстояния помещаются по фазе в первую скобку неоднозначности, тогда как их фактическое местоположение может находиться в любой из скобок. Эта фигура была вдохновлена ​​[1]

Существует три различных подхода к расчету правильного расстояния. Во-первых, камера должна работать на подходящей частоте модуляции, чтобы избежать накрутки фазы, это самый простой подход. Второй подход заключается в использовании измерений на нескольких частотах модуляции, а третий подход заключается в использовании пространственной информации в изображении для прогнозирования правильного расстояния.

Самый простой способ — понизить частоту модуляции до тех пор, пока свертывание фазы не вызовет проблем, поскольку от объектов, находящихся дальше первой скобки неоднозначности, не возвращается сигнал.

Это снижает точность измерения, поскольку фазовый шум постоянен* между частотами, поэтому один и тот же фазовый шум на более низкой частоте приводит к большему шуму на расстоянии. Это основной мотивирующий фактор для использования более высоких частот модуляции.

Эти подходы измеряют две или более частоты для каждого пикселя, чтобы развернуть измерение по фазе. Эти методы основаны на методах фазовой развертки интерферометрии. Пейн и др. al [2] предложил использовать две частоты для развертывания фазы и указал на преимущество использования более высоких частот модуляции.

Новое максимальное расстояние определяется наибольшим общим знаменателем между двумя частотами модуляции, поэтому новая эффективная частота равна

Для двух частот 40 МГц и 50 МГц наибольший общий знаменатель равен 10 МГц, а для 10 МГц максимальное расстояние составляет 15 м по сравнению до 3 м для 50 МГц и 4,5 м для 40 МГц.

Идея состоит в том, что для двух измерений частоты существует единственное расстояние, которое «имеет смысл» (минимизирует ошибку) двух измерений. Развернутые фазы (тета) можно записать как

Где l и k — целые числа, мы хотим выбрать их, чтобы минимизировать разницу расстояний, так как это уравнение равно нулю в бесшумном случае

Поиск грубой силы визуализируется на анимации ниже, где мы вычисляем все возможные l и k значение и вычислить разницу расстояний и найти минимум. Расположение минимума указывает, какие значения l и k следует использовать, чтобы правильно развернуть измерение по фазе.

Рисунок 4: Анимация поиска скобки неоднозначности методом грубой силы. По мере изменения расстояния (зеленый шарик) также меняется скобка неоднозначности для каждой частоты. При каждом изменении изменяется и минимальная разница расстояний. Индекс строки и столбца разницы расстояний кодирует, в каких скобках неоднозначности находится мяч в данный момент.

Описанный выше метод является наивным (грубая сила), поскольку он ищет по всем возможным значениям l и k. Более оптимальным алгоритмом является китайская теорема об остатках [1]. Есть несколько численных улучшений для ускорения поиска, например, вычисление только наиболее вероятных индексов. Адриан Йонгенелен работал над разверткой фазы в рамках своей докторской диссертации [1] и реализовал метод обработки в реальном времени на ПЛИС.

Другой альтернативой китайской теореме об остатках является поиск только по подмножеству возможных индексов. Для пары 40,50 МГц это будет k и l значений (0,0), (0,1), (1,1), (1,2), (2,2), (2,3) ),(3,3) и (3,4), так что поиск осуществляется по 8 парам вместо возможных 20 пар.

Видео ниже демонстрирует развёртку фазы с помощью непрямой времяпролетной камеры Chronoptics Kea, фиксирующей две частоты модуляции, 80 МГц и 100 МГц.

В этом видеоролике показано развертывание фазы в действии с использованием двух частот модуляции, 60 и 80 МГц, и их объединения для увеличения максимального расстояния.

Microsoft подала заявку на патент на многочастотную фазовую развертку [3], разработанную Benedetti et al. Этот подход начинается с наблюдения, что построение графика измеренной фазы одной частоты по отношению к фазе второй частоты приводит к появлению линий на этой поверхности. Измерения должны когда-либо приземляться только на эти строки, и та линия, на которой приземляется измерение, представляет собой смещение расстояния (скобка неоднозначности), поэтому мы можем развернуть измерение по фазе.

Рисунок 5: График зависимости фазы 40 МГц от фазы 50 МГц. Зеленый шар представляет собой расстояние, которое он проходит.

Второе наблюдение состоит в том, что уменьшение размерности возможно путем поворота линий таким образом, чтобы они схлопывались в набор точек.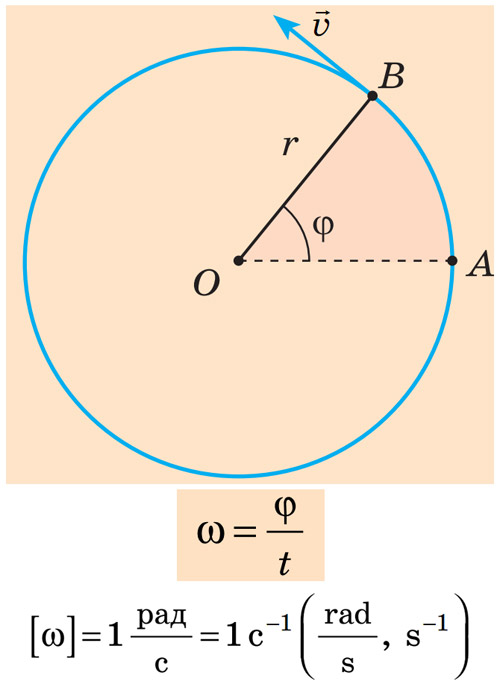 Ближайшая к измерению точка кодирует скобку неоднозначности. Этот подход может быть расширен до нескольких частот модуляции, например, до 3 частот.

Рисунок 6: Уменьшение размерности линий за счет вращения. Набор линий можно свести к набору точек простым поворотом

Для трех частот линии на плоскости становятся линиями в трехмерном пространстве из-за добавления дополнительного измерения. Затем вращение уменьшает размер до точек на 2D-плоскости. Максимальное расстояние по-прежнему определяется наибольшим общим знаменателем (НОД), поэтому для частот [75 МГц, 90 МГц, 120 МГц] НОД составляет 15 МГц, что дает максимальное расстояние 10 м.

Дрёшель и др. al [4] использовал смесь частот и пространственной информации для фазовой развертки, так как доступны две частоты: 29 МГц и 31 МГц. Пространственная информация искала пиксели, расстояние которых прыгнуло на 2π.

Лавин и др. al [5] использовал информацию о частоте с амплитудой и пространственной (соседние пиксели) для более надежной фазовой развертки, удаляя шум «соль и перец», присутствующий при попиксельной развертке фазы в условиях слабого сигнала.

Методы развертки фазы на одной частоте пытаются развернуть фазу на основе информации, содержащейся в измерении одной частоты, с использованием пространственной информации, предоставленной датчиком изображения. Это часто похоже на методы развертывания фазы, используемые для интерферометрических радаров с синтезированной апертурой.

Методы используют следующие идеи/ограничения для развертывания фазы

• Скачки на расстоянии, которые соответствуют 2π между пикселями, скорее всего, являются фазовым свертыванием, и эти скачки могут быть развернуты.
• Поверхности объектов гладкие.
• Предположение о ламбертовских поверхностях, что амплитуда падает на 1/d², поэтому близкие темные объекты, вероятно, имеют фазовую обертку.
• В некоторых сценах (например, в коридоре) мы знаем, что пиксели в нижней части изображения измерены правильно, поэтому мы можем развернуть фазу, следуя градиенту расстояния вниз по коридору, и развернуть фазу любых скачков пикселей, соответствующих 2π.

Докторская диссертация Райана Крэбба [6] была посвящена развёртке одночастотной фазы для измерения глубины ToF. Crabb разработал два метода для развертки фазы одиночного кадра и сравнил свои результаты с Choe et. и др. [7].

МакКлюр и др. al [8] продемонстрировал конвейер обработки для фазовой развертки с одним кадром. МакКлюр начал с классификации пикселей на основе данных об их амплитуде, поскольку амплитуда отражения падает как 1/d², поэтому пиксели с более низкой амплитудой с большей вероятностью будут свернуты по фазе. Затем с конвейером фильтрации для сегментации различных объектов в сцене алгоритм классифицировал каждый объект как свернутый по фазе или без него.

Недостатком одночастотных методов является то, что их можно обмануть. Они хорошо работают в некоторых ситуациях, например, при использовании ToF-камеры в известном сценарии использования, однако они могут быстро выйти из строя при представлении общих сцен.

Благодаря достижениям в области машинного обучения, я уверен, что появится статья об использовании глубокого обучения для решения фазовой развертки на камерах ToF с использованием одной частоты, которая может быть обобщена для лучшего решения. Если вы написали такую ​​статью или планируете, дайте мне знать! В настоящее время подход глубокого обучения к ToF заключается в замене конвейера полной глубины нейронной сетью, такой как DeepToF [9].], из которых часть конвейера является фазовой разверткой.

Наилучший метод развертывания фазы зависит от вашего приложения для измерения глубины. Когда количество кадров должно быть небольшим, а вычислительная мощность ограничена, лучше всего уменьшить частоту модуляции. Когда можно получить больше кадров, становятся возможными многочастотные методы. С этими решениями вычисление на пиксель невелико, а результат является детерминированным. В случае, когда требуется небольшое количество кадров, имеется вычислительная мощность и есть некоторые предсказуемые ограничения сцены, тогда подходят одночастотные методы. Наилучший подход зависит от приложения, которое определяет бюджет мощности, количество кадров в секунду, вычислительную сложность и точность. Поговорите с командой Chronoptics о том, какой метод фазовой развертки лучше! Вы можете написать мне по адресу r.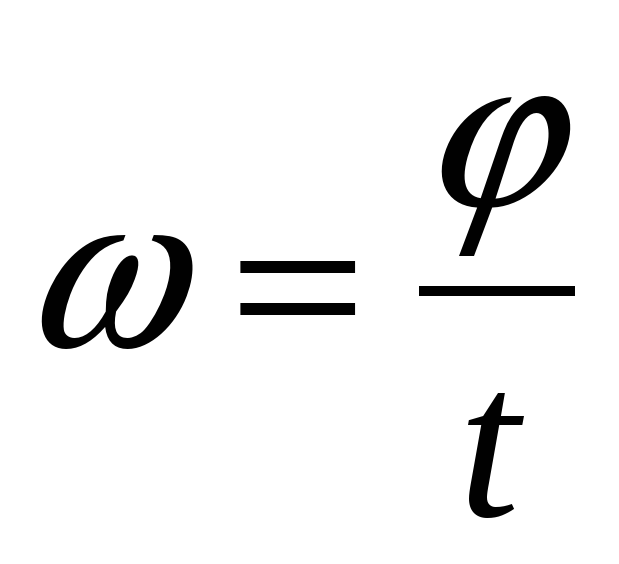 [email protected]

[1] Jongenelen, APP (2011). Разработка компактной, настраиваемой системы визуализации дальности в реальном времени.

[2] Пейн, А. Д., Йонгелен, А. П., Доррингтон, А. А., Кри, М. Дж., и Карнеги, Д. А. (2009). Отображение нескольких частотных диапазонов для устранения неоднозначности измерений. В оптических трехмерных методах измерения.

[3] Бенедетти, А., Перри, Т., Фентон, М., и Могаллапу, В. (2014). Заявка на патент США №13/586,391 .

[4] Дрошель, Д., Хольц, Д., и Бенке, С. (2010, октябрь). Многочастотная фазовая развертка для времяпролетных камер. В 2010 г. Международная конференция IEEE / RSJ по интеллектуальным роботам и системам (стр. 1463–1469).). IEEE.

[5] Лавин, Ф.Дж., Форссен, П.Е., и Оврен, Х. (2016, октябрь). Эффективное многочастотное развертывание фазы с использованием оценки плотности ядра. На Европейской конференции по компьютерному зрению (стр. 170–185). Спрингер, Чам.

[6] Crabb, RE (2015). Быстрое развертывание фазы во времени пролета и сегментация сцены с использованием априорных сцен, управляемых данными (докторская диссертация, Калифорнийский университет в Санта-Круз).

[7] Чой, О., Лим, Х., Канг, Б., Ким, Ю.С., Ли, К., Ким, Дж.Д., и Ким, С.Ю. (2010, сентябрь). Развертка диапазона для времяпролетных камер глубины. В 2010 г. Международная конференция IEEE по обработке изображений (стр. 4189).–4192). IEEE.

[8] МакКлюр, С. Х., Кри, М. Дж., Доррингтон, А. А., и Пейн, А. Д. (2010 г., январь). Устранение неоднозначности измерения глубины с помощью имеющихся в продаже дальномерных камер. В Обработке изображений: приложения машинного зрения III (том 7538, стр. 75380K). Международное общество оптики и фотоники.

[9] Марко, Дж., Эрнандес, К., Муньос, А., Донг, Ю., Харабо, А., Ким, М. Х., … и Гутьеррес, Д. (2017). DeepToF: готовая коррекция многолучевых помех в режиме реального времени при получении изображений во время пролета. Транзакции ACM с графикой (ToG), 36 (6), 1–12.