Содержание
Физика. Период и частота | Частная школа. 9 класс
Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.
Конспекты по физике Учебник физики Тесты по физике
Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.
ПЕРИОД
Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.
Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.
С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.
Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.
ЧАСТОТА
Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.
Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?
Очевидно, ν = 1/Т = 1/20 1/с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.
е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.
Таким образом, частота обращения является величиной, обратной периоду обращения:
Именно поэтому единица этой физической величины обратна секунде, т. е. 1/с, или с-1.
СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:
или с учётом формулы (1):
С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:
Часто мгновенную скорость движения по окружности называют линейной скоростью.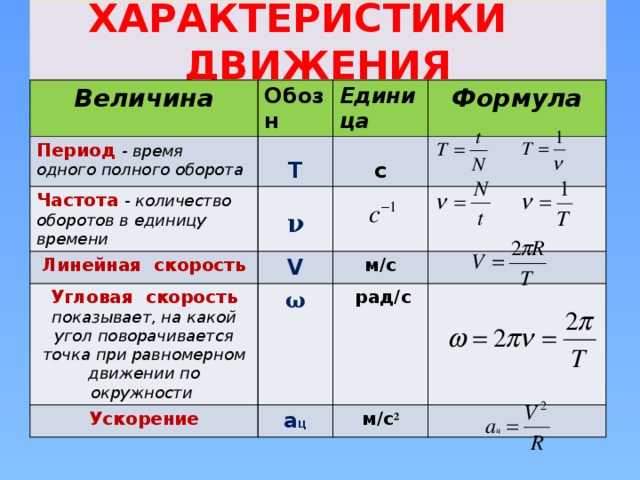
Модуль скорости движения тела по окружности рассчитывается по формуле:
Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.
РЕШЕНИЕ ЗАДАЧ
Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.
Ответ: υ = 0,722 м/с.
Задача 2. Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 106 км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.
Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.
Ответ: υ ≈ 30 км/с.
Вы смотрели Конспект по физике для 9 класса «Период и частота».
Вернуться к Списку конспектов по физике (Оглавление).
6.14 Определить частоту вращения (циклотронную частоту) частицы массы m и зарядом q в магнитном поле индукции b.
Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость
лежит в плоскости, перпендикулярной
вектору магнитной индукции
то
частица будет двигаться по окружности
радиуса:
(6.14.1)
где
m,v,q
– масса, скорость и заряд частицы.
Сила
Лоренца в этом случае играет роль
центростремительной силы .
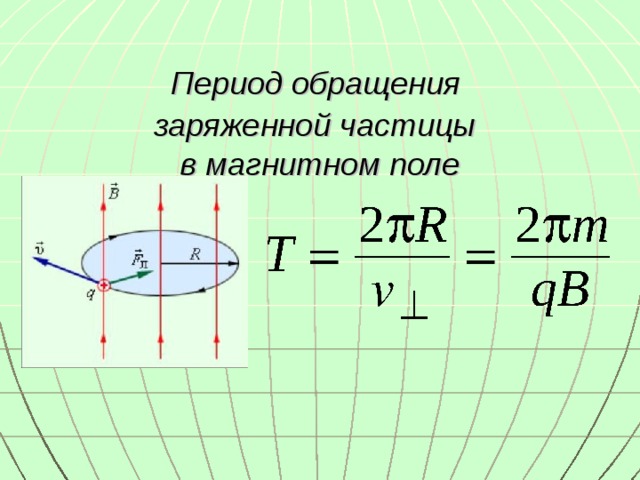
Период
обращения частицы в однородном
магнитном
поле равен:
Это
выражение показывает, что для заряженных
частиц заданной массы m
период обращения не зависит от скорости
υ
и радиуса траектории r.
Угловая
скорость движения заряженной частицы
по круговой траектории:
(6.14.2)
Подставим
в полученное выражение (6.14.2) выражение
для радиуса траектории частицы (6.14.1),
получим:
называется
циклотронной
частотой.
Циклотронная частота не зависит от
скорости (следовательно, и от кинетической
энергии) частицы. Это обстоятельство
используется в циклотронах
– ускорителях тяжелых частиц (протонов,
ионов).
6.15 Выполняется ли принцип независимости движения для заряженных частиц, движущихся одновременно в электрическом и магнитном полях?
Движение
частицы, находящейся в электромагнитном
поле, описывается следующим уравнением.
Второй
закон Ньютона:
Заряженная
частица, обладающая зарядом q,
движется в электромагнитном поле
согласно этому уравнению. Видим, что
сила, действующая на частицу со стороны
электромагнитного поля, определяется
двумя векторными полями: поле
называется
напряжённостью электрического поля,
поле
— индукция магнитного поля.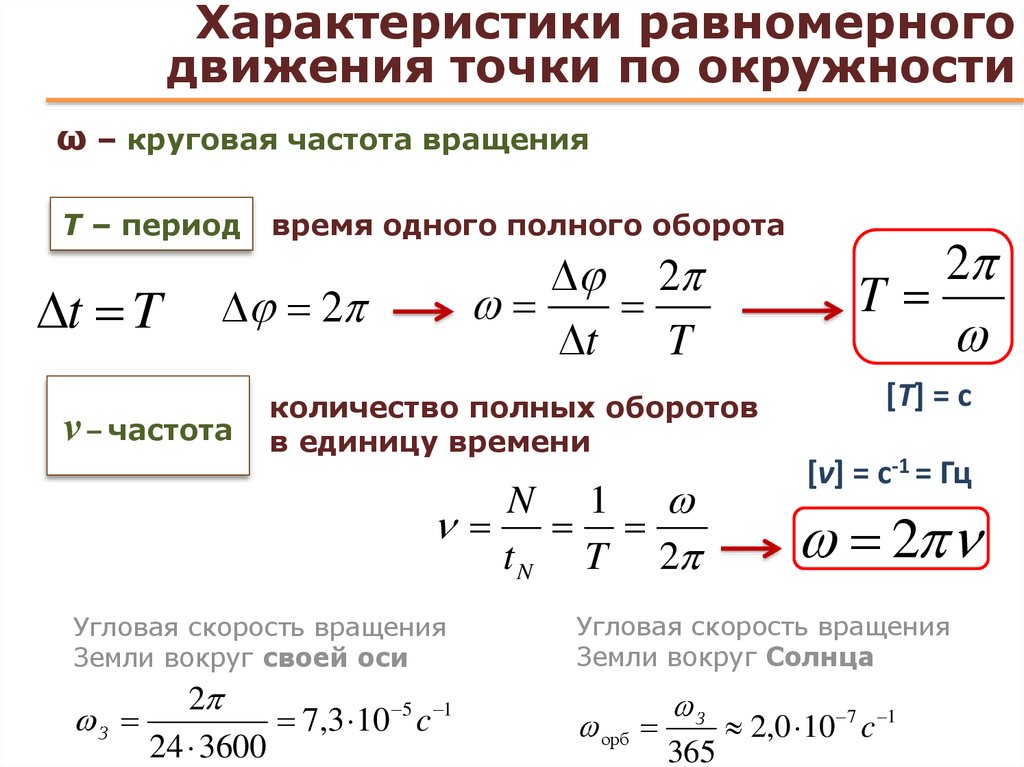 Они разделены,
Они разделены,
потому что влияние их на частицу различны.
Поле
не
содержит никаких характеристик частицы
кроме заряда. Если v
= 0, то второе слагаемое обращается в
ноль. Это означает, что магнитное поле
действует только на движущиеся частицы.
Неподвижные заряды не чувствуют
магнитного поля.
Следовательно,
принцип независимости движения для
заряженных частиц, движущихся одновременно
в электрическом и магнитном полях,
выполняется.
6.16
Электрон, обладающий скоростью v, попадает
в однородное магнитное поле, индукция
которого перпендикулярна скорости v.
Окружность, какого радиуса описывает
электрон?
Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость
лежит в плоскости, перпендикулярной
вектору магнитной индукции
то
частица будет двигаться по окружности
радиуса:
где
m,
q
– масса и заряд частицы.
Заряд
электрона q
= e,
масса m
= me.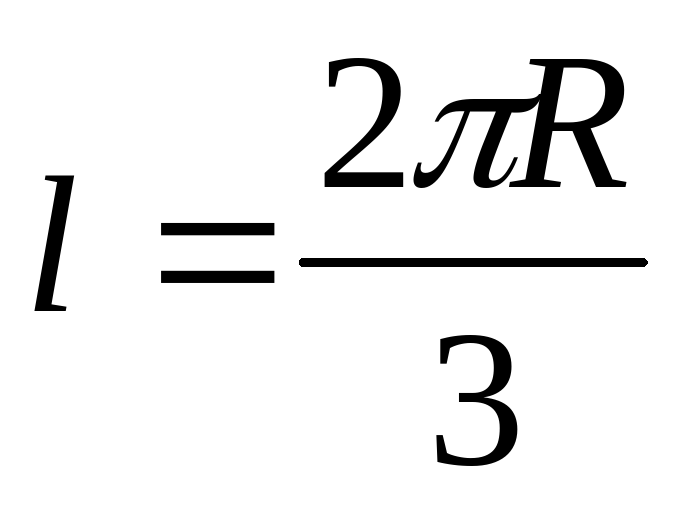
Радиус
описываемой электроном окружности:
6.17
Заряженная частица, пролетая некоторую
область пространства, не отклоняется
от первоначального направления движения.
Можно ли на основании этого факта
утверждать, что магнитное поле в этой
области отсутствует?
Нельзя.
Заряженная частица не отклоняется от
первоначального направления движения
в магнитном поле в следующих случаях:
1)
В каждой точке магнитного поля существует
такое направление, вдоль которого на
движущуюся заряженную частицу магнитная
сила не действует. Это направление можно
назвать магнитной осью.
Существенно,
что для каждой точки поля существует
свое, отличное от других точек поля,
направление магнитной оси. Это направление
выбирают за направление вектора магнитной
индукции
.
При
движении вдоль линий поля (угол между
скоростью
и вектором
магнитной индукции
равен нулю) на частицу не действует сила
— она движется прямолинейно.
2)
На частицу, движущуюся в скрещенных
электрическом и магнитном полях,
действуют электрическая сила
и
магнитная
сила Лоренца.
При условии E = υB
эти силы точно уравновешивают друг
друга. Если это условие выполняется,
частица будет двигаться равномерно и
прямолинейно.
6.18
Пучок протонов, попадая в некоторую
область пространства, отклоняется на
некоторый угол. Можно ли на основании
этого факта определить, каким полем
вызвано отклонение, электрическим или
магнитным?
Не
имея данных ни о направлении поля
действия поля, ни об изменении скорости
частиц (или их кинетической энергии)
при прохождении данной области установить
природу поля нельзя.
6.19
Протон и электрон, имеющие одинаковую
скорость, попадают в однородное магнитное
поле, индукция В которого перпендикулярна
скорости частиц. Как будут различаться
их траектории?
Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость
лежит в плоскости, перпендикулярной
вектору магнитной индукции
то частица будет двигаться по окружности
радиуса:
(6. 19.1)
19.1)
где
q,
m
– заряд и масса частицы.
Заряды
протона и электрона равны по величине,
но противоположны по знаку: |qp|
= |qe|
= |e|
Исходя
из формулы 6.19.1 радиус траектории частицы
пропорционален ее массе и при равенстве
скоростей, радиус траектории протона
будет больше радиуса траектории электрона
примерно в 1836 раз (соотношение масс
протона и электрона mp/me
= 1836,15267).
Так
как эти частицы имеют противоположные
по знаку заряды, то и направление силы
Лоренца, действующий на них в магнитном
поле будет противоположно. Протон и
электрон будут двигаться по окружностям
в противоположных направлениях.
6.20
Протон и электрон, ускоренные одинаковой
разностью потенциалов, влетают в
однородное магнитное поле. Во сколько
раз радиус кривизны траектории протона
будет больше радиуса кривизны траектории
электрона?
Частица,
пройдя ускоряющую разность потенциалов
U,
приобретает кинетическую энергию,
равную:
(6. 20.1)
20.1)
где
q,
m
– заряд и масса частицы;
v
– скорость, которую приобретает частица.
Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость
лежит в плоскости, перпендикулярной
вектору магнитной индукции
то
частица будет двигаться по окружности
радиуса:
(6.20.2)
Из
уравнения (6.20.1) найдем скорость частицы:
Полученное
выражение для скорости частицы
v
подставим в уравнение (6.20.2):
(6.20.3)
Заряды
протона и электрона равны по величине
и противоположны по знаку: |qp|
= |qe|
= |e|
С
учетом равенства абсолютной величины
зарядов и на основании формулы (5.20.3)
запишем соотношение радиусов кривизны
траекторий частиц:
В
справочной литературе приведено
соотношение масс протона и электрона
− mp/me
= 1836,15267.
Окончательно
получаем:
Центростремительная сила — Резюме — Гиперучебник по физике
[закрыть]
| Сила, которая… | создаст движущийся объект |
или… |
|---|---|---|
| параллельно скорости |
изменить скорость (ускорить) | ускорить (в обычном смысле этого слова) |
| антипараллельно скорости |
изменить скорость (замедлить) | замедлить (это еще один способ ускориться) |
| перпендикулярно скорости |
изменить направление (повернуть) | ускорение центростремительно (что также является еще одним способом ускорения) |
- A центростремительное ускорение ( a c )
- возникает всякий раз, когда движущийся объект меняет направление
- не меняет скорость объекта
- действует под прямым углом к скорости в любой момент
- направлен к центру круга (поиск центра)
- также известен как радиальное ускорение
.

- A центростремительная сила ( F c )
- это сила, которая заставляет движущийся объект менять направление
- — это не конкретная сила, а название, данное любой силе или комбинации сил, ответственных за центростремительное ускорение
- действует под прямым углом к скорости в любой момент
- направлен к центру круга (поиск центра)
- также известен как радиальная сила
.
- Направления в круговом движении
- Скорость ( v ) является касательной (лежит по касательной к траектории).
- Центростремительное ускорение и центростремительная сила бывают центростремительными (направлены к центру окружности) или радиальными (находятся на радиусе окружности).
- Центростремительное ускорение перпендикулярно скорости.
- Центростремительная сила параллельна центростремительному ускорению.
- Уравнения [в единицах СИ]
- скорость и скорость
линейные количества v = 2π р Т где v = скорость [м/с] π = математическая константа r = радиус кругового пути [м] Т = период обращения [с] угловые величины v = ω × r где v = вектор поступательной скорости [м/с] r = радиус-вектор [м] ω = вектор угловой скорости [рад/с] - частота и период
линейные количества ƒ = 1 Т где f = частота вращения [Гц = 1/с = с −1 ] Т = период обращения [с] угловые величины ω = 2π = 2πƒ Т где ω = величина угловой скорости или угловой частоты [рад/с] π = математическая константа Т = период обращения [с] f = частота вращения [Гц = 1/с = с −1 ] - центростремительное ускорение
линейные количества а в = v 2 = 4π 2 р р Т 2 где а в = центростремительное ускорение [м/с 2 ] v = скорость [м/с] r = радиус кругового пути [м] π = математическая константа Т = период обращения [с] угловые величины .

A C = −ω 2 R = ω × V где а в = вектор центростремительного ускорения [м/с 2 ] ω = величина угловой скорости или угловой частоты [рад/с] r = радиус-вектор [м] ω = вектор угловой скорости [рад/с] v = вектор поступательной скорости [м/с]
- скорость и скорость
- А центробежная сила …
- это вымышленная сила (он же кажущаяся сила или псевдосила )
- не является результатом взаимодействия между объектами
- перестает существовать, когда объект перестает двигаться по кругу
- — иллюзия во вращающейся системе отсчета
- кажется направленным от центра круга (центр убегает)
.
- Круговое движение, при котором скорость постоянна, называется равномерным круговым движением .

Калькулятор кругового движения
Автор Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 01 ноября 2022 г.
Содержание:
- Определение кругового движения
- Что такое равномерное круговое движение?
- Как рассчитать параметры кругового движения?
- Формулы кругового движения
- Часто задаваемые вопросы
Калькулятор кругового движения Omni позволяет рассчитать все параметры равномерного кругового движения . Если вы не знаете, что такое равномерное круговое движение, или чувствуете себя подавленным формулами кругового движения, не волнуйтесь! Наш калькулятор кругового движения поможет вам понять концепции равномерного кругового движения в физике.
Читайте дальше, чтобы узнать определение, примеры и формулы кругового движения. Вы также найдете примеры расчета параметров кругового движения (таких как период, частота, скорость и ускорение) с помощью нашего калькулятора равномерного кругового движения.
Если вас больше интересует определение момента вращения объекта, посетите наш калькулятор углового момента.
Определение кругового движения
Когда объект движется по круговой траектории , мы называем его движение круговым. Некоторые распространенные примеры кругового движения:
- Гоночный автомобиль движется по круговой кривой;
- Искусственный спутник, вращающийся вокруг Земли;
- Наконечник минутной/секундной стрелки часов; и
- Вращение камня, привязанного к веревке.
Круговое движение объекта может быть равномерным круговым движением или неравномерное круговое движение .
При круговом движении направление движения постоянно меняется . В любой момент направление движения тела, движущегося по окружности, лежит по касательной к окружности в этот момент.
Более простой способ визуализировать эту концепцию — представить себе вращающийся камень, привязанный к веревке; когда струна рвется, камень летит по касательной.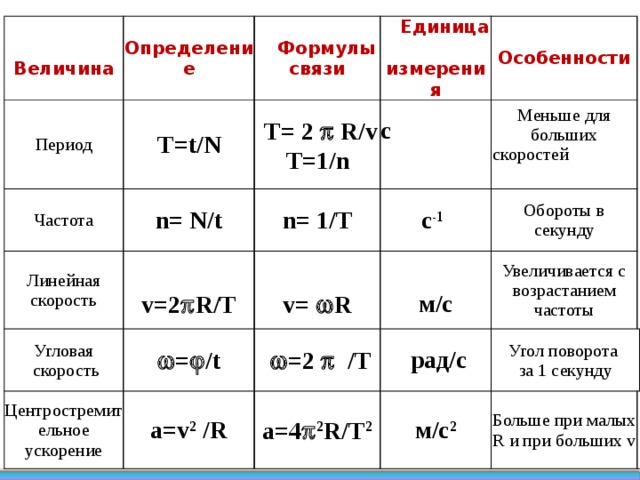
Что такое равномерное круговое движение?
При равномерном круговом движении объект движется по круговой траектории со скоростью постоянная скорость . Это означает, что объект будет проходить равные расстояния по окружности окружности за равные промежутки времени. В неравномерном круговом движении скорость объекта изменяется .
Хотя при равномерном круговом движении скорость постоянна, направление движения постоянно меняется, как мы обсуждали в предыдущем разделе. Следовательно, скорость объекта, совершающего равномерное круговое движение, также непрерывно изменяется (см. рисунок 1).
Рис. 1: Скорость, ускорение и угловая скорость при равномерном круговом движении. (Источник: wikimedia.org) .
Из-за изменения направления скорости объект испытывает ускорение, называемое центростремительным ускорением .
Из первого закона движения Ньютона мы знаем, что тело не может изменить направление своего движения само по себе. Для этого необходима внешняя сила. Эта внешняя сила , которая удерживает объект, движущийся по круговой траектории называется центростремительной силой . Вы можете узнать больше об этой силе в нашем калькуляторе центростремительной силы.
Для этого необходима внешняя сила. Эта внешняя сила , которая удерживает объект, движущийся по круговой траектории называется центростремительной силой . Вы можете узнать больше об этой силе в нашем калькуляторе центростремительной силы.
Как рассчитать параметры кругового движения?
Давайте посмотрим, как использовать калькулятор равномерного кругового движения для расчета различных физических параметров кругового движения.
- Используйте раскрывающееся меню . Мы выберем параметр радиус, скорость и ускорение, поскольку мы хотим рассчитать все параметры для этого примера.
- Введите период времени кругового движения, скажем, 4 секунды в строке 1.
- Калькулятор отобразит частоту ( 0,25 Гц ) и угловую скорость ( 1,571 рад/с ) кругового движения.
- Введите радиус кругового пути, например 2 метра , в строке 2.
 Калькулятор покажет скорость ( 3,142 м/с ) и центростремительное ускорение ( 4,935 м/с² ).
Калькулятор покажет скорость ( 3,142 м/с ) и центростремительное ускорение ( 4,935 м/с² ).
Мы также рекомендуем воспользоваться нашим калькулятором центробежной силы.
Формулы движения по окружности
Рассмотрим объект, движущийся по окружности радиуса rrr (см. рис. 1) с центром в точке O . Пусть объект перемещается (против часовой стрелки) из P в Q за время ttt. Физические величины, описывающие это движение, и формулы для кругового движения:
Рис. 1: Движение объекта по круговому пути.
-
Угловое смещение (θ\thetaθ) — это угол θ\thetaθ, образуемый в центре радиус-вектором за заданное время. Мы знаем, что:
угол=дуга/радиус\rm угол = дуга/радиусугол=дуга/радиус
… следовательно, для цифры 1 мы можем написать:
θ=PQ/r\тета = PQ/rθ=PQ/r
Единицей углового смещения в системе СИ является радиан (рад \text{рад}рад).

-
Период времени (ТТТ) — это время, за которое объект совершает один оборот по круговой траектории. Единицей периода времени в системе СИ является секунда (s\rm ss).
-
Частота (ν\nuν) — количество оборотов объекта за одну секунду. Единицей частоты в системе СИ является герц (Гц \rm Гц).
ν=1/T\nu = 1/Tν=1/T
-
Угловая скорость (ω\omegaω) — скорость изменения углового смещения со временем, т. е.
ω=Δθ/Δt\omega = \Delta \theta/ \Delta tω=Δθ/Δt
Единицей угловой скорости в системе СИ является радиан в секунду (рад/с\rm рад/срад/с).
Когда объект совершает один оборот (см. рис. 1), угол в центре составляет 2π2 \pi2π радиан. Это означает, что для периода кругового движения t=Tt = Tt=T, θ=2π\theta = 2 \piθ=2π. Следовательно, мы можем выразить угловую скорость как:
ω=2π/T\omega = 2 \pi / Tω=2π/T
…или:
ω=2πν\omega = 2 \pi \nuω=2πν
-
Угловое ускорение (α\alphaα) — скорость изменения угловой скорости во времени, т.
 е.
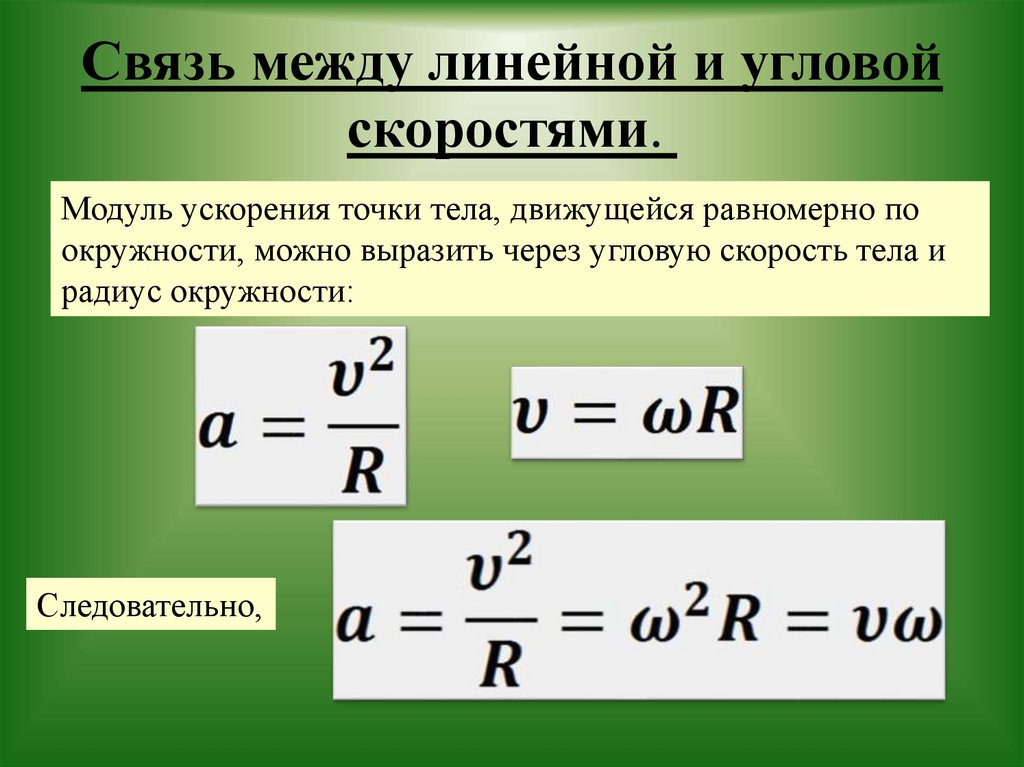
е.92/rαc=v2/r
Часто задаваемые вопросы
Что является постоянным в равномерном круговом движении?
Скорость постоянна при равномерном круговом движении. Объект движется с постоянной скоростью по круговой траектории в равномерном круговом движении.
Какая центростремительная сила действует на объект, движущийся по окружности?
Центростремительная сила — это сила, которая действует на любой объект, движущийся по окружности . Величина центростремительной силы, действующей на объект, движущийся по окружности, равна произведению его массы на центростремительное ускорение. Центростремительная сила направлена к центру окружности.
Какая связь между линейной скоростью и угловой скоростью?
Для объекта, совершающего равномерное круговое движение, линейная скорость v равна произведению угловой скорости ω и радиуса пути r .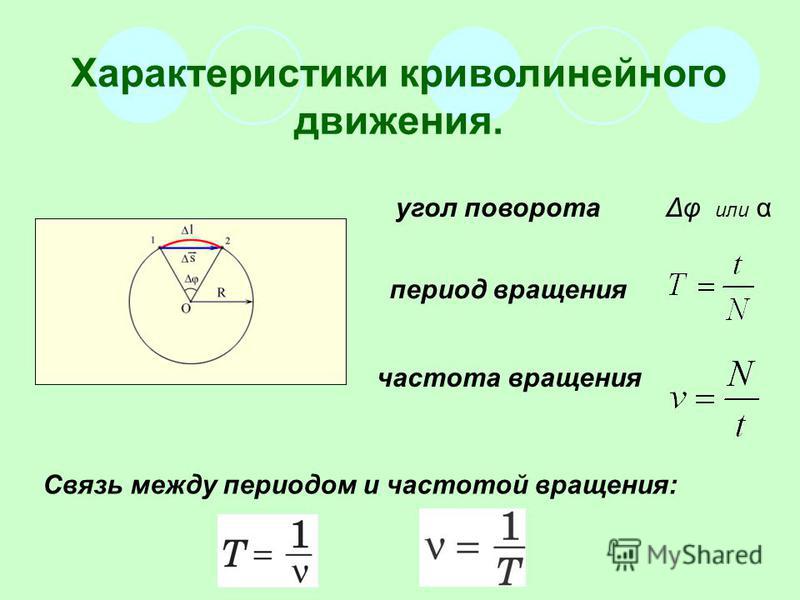


 Калькулятор покажет скорость ( 3,142 м/с ) и центростремительное ускорение ( 4,935 м/с² ).
Калькулятор покажет скорость ( 3,142 м/с ) и центростремительное ускорение ( 4,935 м/с² ).

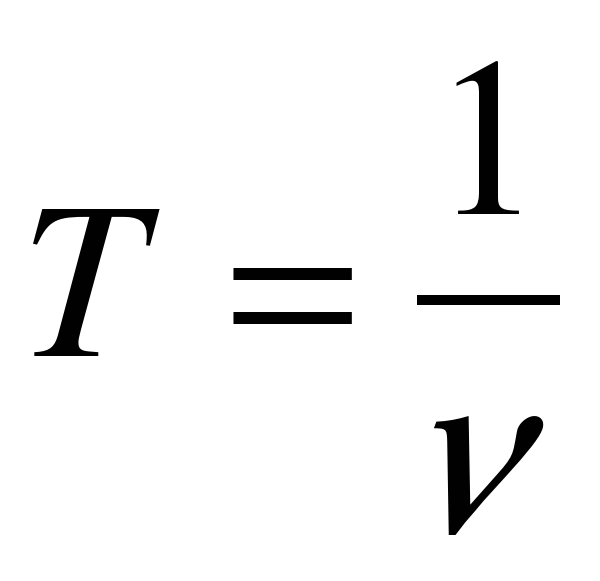 е.
е.