Содержание
Линейная скорость | формула и расшифровка
2709
3
3 мин. на чтение
Понимание любого понятия в физике предполагает расшифровку определения связанных терминов. Таким образом, в случае линейной скорости становится необходимым определить линейную скорость и скорость по отдельности.
Линейная скорость относится к движению объекта по прямой линии или по заданной оси. С другой стороны, скорость означает расстояние, которое движущееся тело проходит в определенном направлении за определенное время. Таким образом, сочетание этих двух определений поможет вам понять основную концепцию линейной скорости.
Что такое скорость?
Термин «скорость» может использоваться в различных областях, включая физику, термодинамику, химию и т.
д. Прежде чем мы перейдем к пониманию линейной и угловой скорости, мы сначала определим скорость как отдельный термин.
Скорость можно объяснить как скорость изменения положения объекта в течение определенного срока или диапазона времени, ее можно разделить на два типа: угловая скорость и линейная скорость. Чтобы определить скорость, мы возьмем пример, поэтому представьте, что вы едете по дороге и смотрите на приборную панель или любые вывески во время движения, спидометр показывает, что автомобиль движется со скоростью 65 км в час, тогда мы можем сказать, что скорость 65 км в час — это скорость, которая представляет собой скорость изменения км по отношению к часам, которые мы видим. Формула скорости равна расстоянию, деленному на время, может рассчитать линейную скорость объекта. В формуле v обозначает линейную скорость, d обозначает пройденное расстояние, а t обозначает время.
Теперь, возвращаясь к ее различным типам, линейная скорость — это просто скорость изменения положения объекта, который движется по прямому пути, поэтому любой движущийся объект имеет линейную скорость, с другой стороны, угловая скорость применяется только или может применяться к объектам, которые движутся по круговой траектории, а также может быть определена как скорость изменения углового смещения во времени.
Угловая скорость, измеряемая в рад/с, которая также может быть преобразована в градусы, представляет собой изменение угла во времени. v=rω для расчета линейной скорости по угловой скорости.
V = ωr, где ω равно радианам в секунду, а r — радиус.
Если период вращения равен t, то ω=2π/t. Как результат, v=2π∗r/t.
Линейную скорость можно испытать в повседневной жизни, поскольку мы видим так много движущихся объектов, которые имеют линейную скорость, таких как человек, идущий на прогулку, вождение, бег или езду на велосипеде, всегда может быть линейная скорость, которая может наблюдаться. Кроме того, бывают случаи, когда объект может двигаться по прямому пути с заданной постоянной скоростью, это можно сказать, что объект движется с постоянной линейной скоростью, проще говоря, мы можем сказать, что скорость Лены объекта не изменяется и, следовательно, постоянный. Линейная скорость, измеряемая в м/с, — это скорость по прямой.
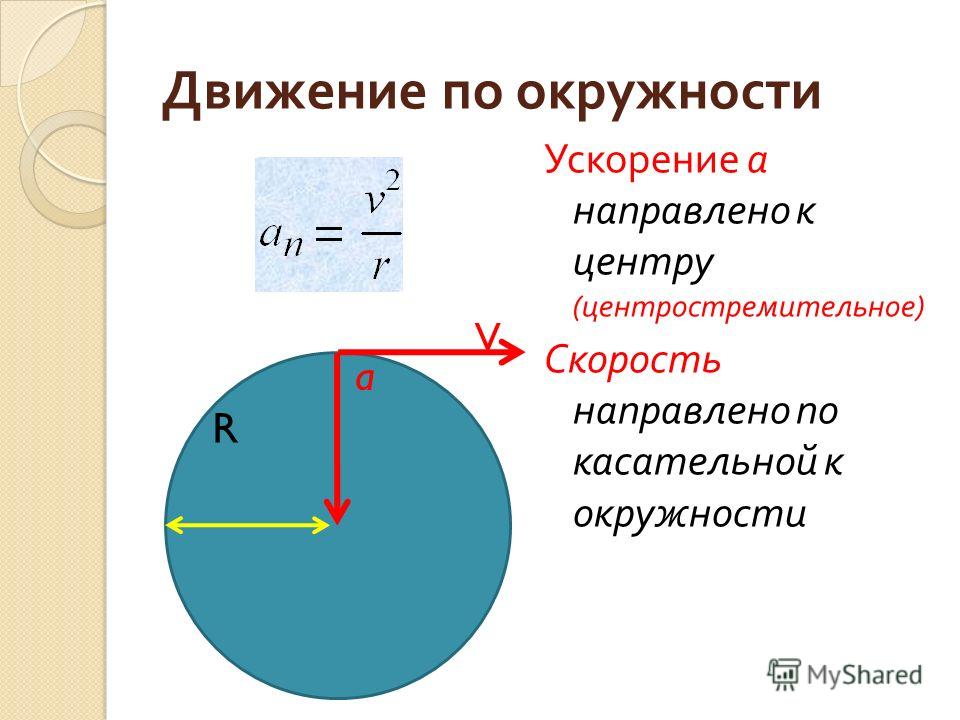
Когда мы говорим об окружности, связь между дугой на окружности и углом, на который она опирается, измеренным в излучении, позволяет нам определить величины, связанные с движением по окружности, и благодаря этому также мы можем сказать, что объекты, движущиеся по круговой траектории, относятся к типу 2. скорости, когда линейна, а другая — угловая скорость, как упоминалось выше. В дополнение к этому мы также можем понимать равномерное круговое движение. Равномерное круговое движение может определять линейную скорость, которая измеряет изменение длины дуги с течением времени.
Когда мы говорим о круговом движении, мы также говорим о направлении линейной скорости. Теперь направление скорости частицы Салина является тангенциальным к круговому пути, который мы видим в любой данной точке этого кругового движения. Направление играет очень важную роль в определении изменения характеристик, скорость является физической векторной величиной, что означает, что для ее правильного определения требуются как величина, так и направление, поэтому, если происходит изменение скорости, направления или того и другого, меняется философия объекта, и тогда мы говорим, что объект является ускоренным движением или ускоряется.
Что такое линейная скорость?
В самом основном смысле определение линейной скорости связано с измерением скорости объекта, когда он движется в определенном направлении. Следовательно, это относится к смещению объекта во времени.
Однако объект должен двигаться по определенной прямой линии. Единицей линейной скорости в системе СИ является метр в секунду или м/с (мс- 1 ).
С другой стороны, размерная формула линейной скорости имеет вид M 0 L 1 T 1
Кроме того, вы должны знать, что это векторная величина, что указывает на то, что она имеет направленный характер.
Какая формула линейной скорости?
Нет никаких различий между обычной скоростью и линейной скоростью, поскольку обе они являются векторными величинами.
Следовательно, формула линейной скорости – ν = d/t
Например, предположим, что движущийся объект преодолевает расстояние 500 метров по прямой линии за 10 секунд.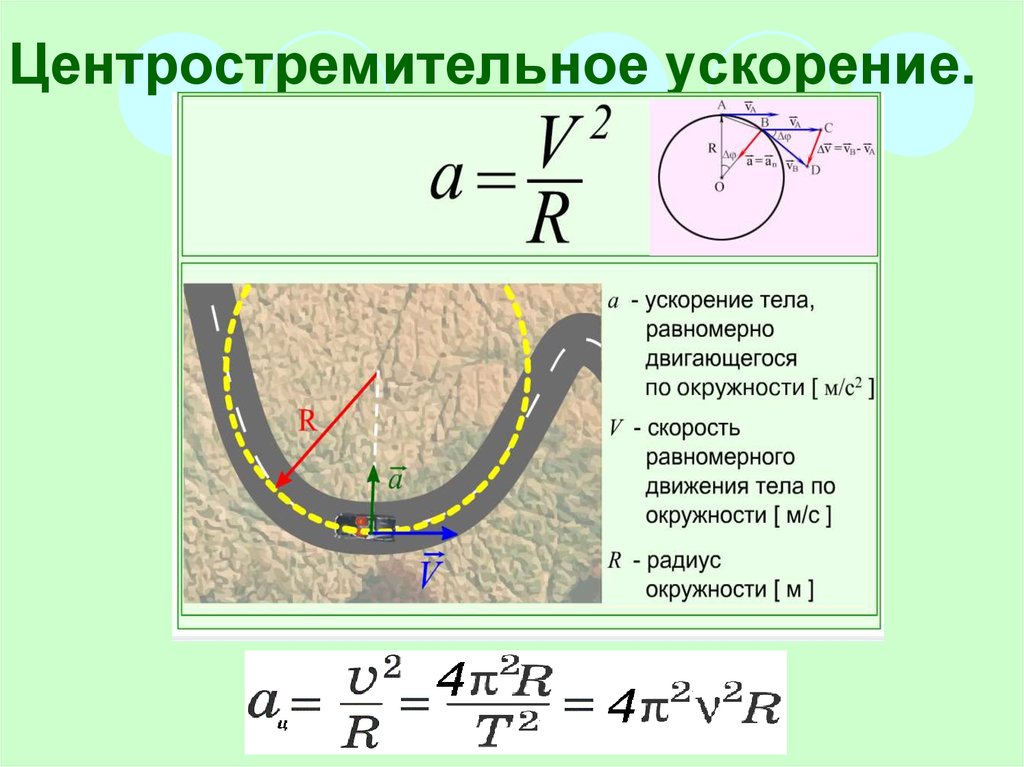
В этом случае линейная скорость объекта равна –
ν = 500 метров/10 секунд = 50 м/с или 50 мс- 1 .
Логически говоря, линейная скорость также применяется к объекту, который движется в круговом направлении, следуя геометрическому месту. В этом случае она называется угловой скоростью.
Криволинейное движение
несколько идей и примеров проблем
Как найти тангенциальную скорость? Это наиболее часто задаваемый вопрос с точки зрения вращательного движения или любого объекта при круговом движении.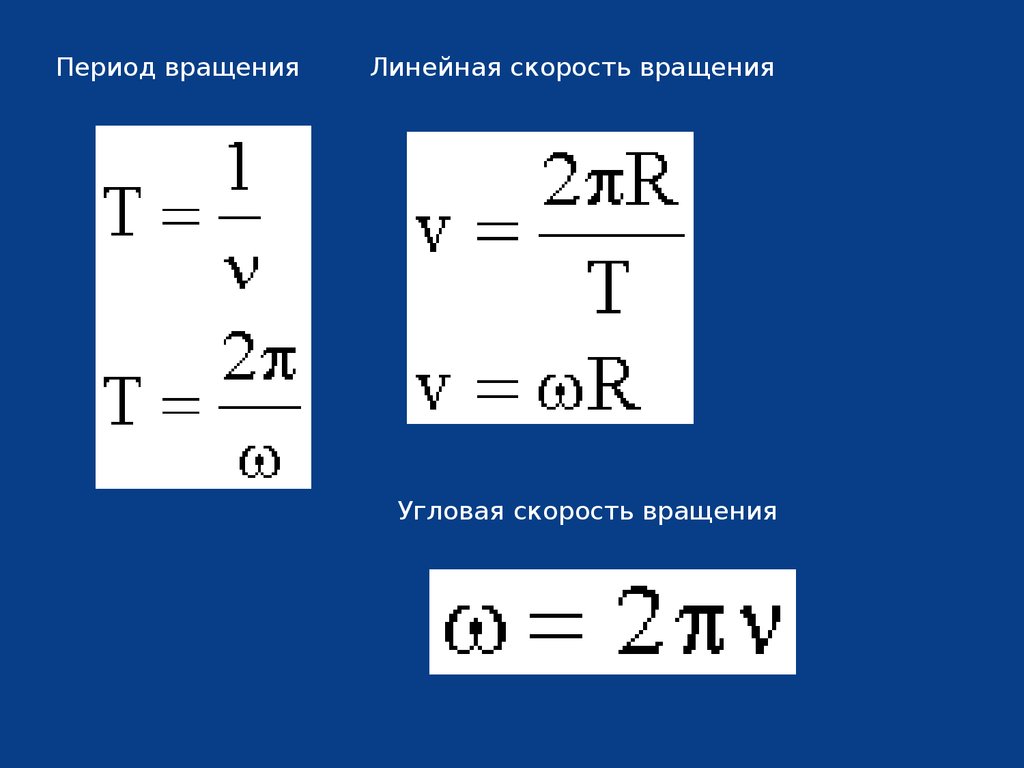
Тангенциальная скорость используется для расчета движения по круговой траектории.
Когда мы говорим, что тело находится в движении, если оно совершает круговое движение, говорят, что оно имеет скорость. Эту скорость можно рассматривать как угловую, так и тангенциальную.
Теперь, когда тело совершает круговое движение, говорят, что касательная является точкой движения. В данной конкретной точке рассчитывается касательная скорость. Направление тангенциальной скорости всегда совпадает по фазе с точкой на объекте, которая на самом деле является касательной.
Когда тело совершает круговое движение, движение на краю круга в основном является касательной в данной точке. Обычно, когда линия проводится рядом с край круга, точка, касающаяся окружности, называется касательная линия.
Формула для тангенциальной скорости дается произведением угловой скорости и радиуса объекта при круговом движении. Когда происходит ускорение это связано с изменением тангенциальная скорость.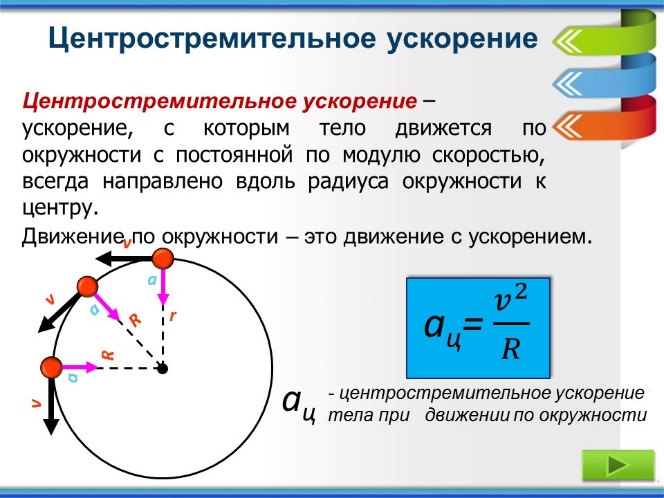
Тангенциальная скорость определяет движение края любого кругового движения и скорость, с которой объект движется вращательным образом. Обычно тангенциальная скорость — это линейный член с угловой скоростью.
«Photogamer — круг на велосипеде!» by Bre Pettis под лицензией CC BY-NC 2.0
Как найти тангенциальную скорость с радиусом?
Видите ли, всякий раз, когда тело находится в движении, мы склонны погружаться в несколько факторов, которые способствуют движению тела. Когда тело находится в движении, мы склонны рассматривать трение, импульс, импульс и так далее.
В основном это факторы, которые способствуют движению тела. Но что приводит в движение тело — это главный вопрос. Таким образом, к телу приложена сила, которая будет двигаться дальше.
Теперь нам нужна скорость, которая приведет тело в движение. Поэтому, когда есть скорость в данный конкретный момент времени, она также будет изменяться. Итак, когда есть скорость присутствует на краю круга, это называется тангенциальная скорость.
Теперь нам нужно определить радиус круглого тела. Линейная или тангенциальная скорость относится явно к мере изменения величины скорости, но не к направлению.
Формула для тангенциальной скорости через радиус: Vt = rx ω. Vt — тангенциальная скорость, r — радиус, ω — угловая скорость.
Задача о радиусе, связанном с тангенциальной скоростью
Проблема:
Если угловая скорость автомобильного колеса составляет 54 рад / с, а радиус колеса равен 0.24 м. какая будет тангенциальная скорость?
Решение:
Vt = rx ω
Vt = 54 х 0.24
Vt = 12.96 м / с
Как найти тангенциальную скорость без учета времени?
Как найти тангенциальную скорость без учета времени — это вопрос ответа на стандартную формулу. Когда тело движется с постоянная скорость, оно будет продолжаться в том же направлении до тех пор, пока не будет приложена внешняя сила.
Определение скорости становится простым, когда тело движется по прямой линии, потому что мы знаем время и расстояние до конкретной ситуации, когда движение считается линейным и прямым, поэтому расчет с заданными деталями значительно проще.
Когда мы рассматриваем движение по окружности или вращательное движение, скорость теперь будет рассматриваться как угловая скорость. Так что в такой ситуации есть способ найти скорость на краю кругового движения.
Было показано, что окружности действительно имеют края на своих путях, поэтому вычисление скорости в этой конкретной точке известно как тангенциальная скорость. Эта скорость находится в направлении движения по круговой траектории.
Нам нужно знать, задействовано ли в этом сценарии время. Итак, давайте посмотрим, что в этом деле нет времени, и, следовательно, как найти тангенциальная скорость.
Рассмотрим пример. Пусть транспортное средство движется так, что его колеса имеют угловая скорость 20 рад/с с тангенциальной скоростью 40 м/с. Найдите радиус колеса? Решение этой проблемы простое.
Мы знаем, что формула тангенциальной скорости имеет вид Vt = rx ω. Итак, 40 = rx 20; г = 2м. Вычисляем тангенциальную, угловую или радиусную, не привлекая к задаче время.
«транспортные средства» by восьмеричный под лицензией CC BY 2.0
Как найти тангенциальную скорость по угловой скорости?
В основном здесь мы имеем дело с общим круговым движением. Поэтому, когда тело находится в движении, мы стараемся следить за деталями минут. Следовательно, мы должны знать, что угловая скорость — это главный компонент, приводящий тело в движение.
Следовательно, нам нужно знать все компоненты, ответственные за движение тела при круговом движении. Когда тело движется с постоянной скоростью по кругу, линейная составляющая называется тангенциальной скоростью.
Таким образом, с точки зрения кругового движения, говорят, что это угловая скорость, поскольку здесь участвуют такие факторы, как длина окружности, диаметр и радиус. Однако, пока мы выводим формулу для расчета скорости тела при круговом движении, нам нужно знать о факторах.
Угловая скорость изменение смещения вращающееся тело в заданный интервал времени, когда время.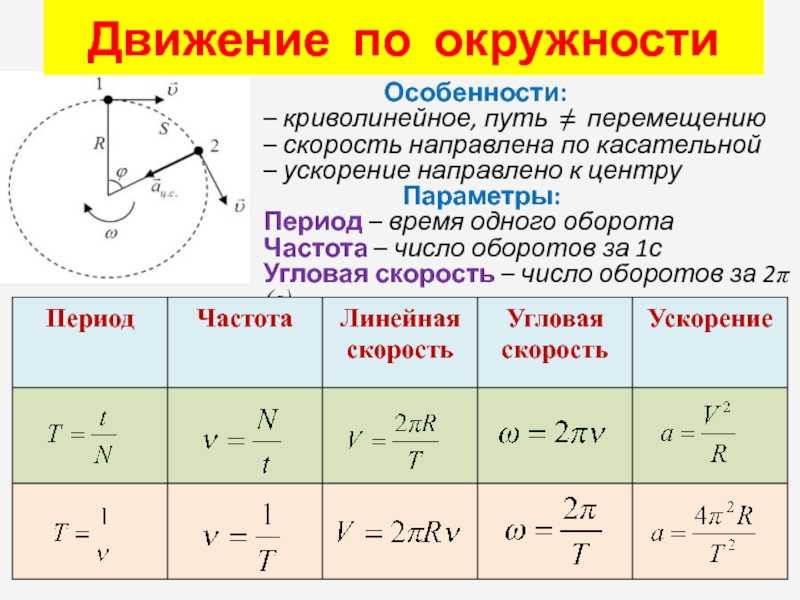
Когда меняется время, меняется и смещение, и движение имеет тенденцию к изменению.
Итак, во вращающемся теле линейная составляющая скорости считается тангенциальной скоростью, и как мы ее вычисляем, очень просто. Нам нужно учитывать радиус тела и его угловую скорость.
Формула такая же и для этого. Итак, давайте посмотрим на это на простом примере. Колесо движется с тангенциальной скоростью 68 м / с с 8m. Рассчитайте угловую скорость колеса.
Ответ прост: 8.5рад / с. И это рассчитывается по формуле Vt = rx ω. Превалирующая формула используется для решения любой другой проблемы, когда это необходимо.
«колесо» by радио1фан21 под лицензией CC BY-NC-ND 2.0
Как найти тангенциальную скорость с центростремительным ускорением?
Центростремительное ускорение на самом деле ничего не дает для тангенциальной скорости. Одной из основных причин, почему тело продолжает двигаться по окружности, является наличие центростремительная сила.
Центростремительная сила в большей или меньшей степени представляет собой толкающую и притягивающую силу.
Движение тела по криволинейной траектории или вращательное движение также можно описать как тангенциальную скорость. Таким образом, центростремительная сила удерживает тангенциальную скорость на месте. Должна быть некоторая сила, которая удерживает вращающееся тело на изогнутых траекториях.
Когда тело совершает круговое движение, тангенциальная скорость определяет движение вращающегося тела. Если центростремительная сила отсутствует, тело упадет на землю. В противном случае движение будет идти в ногу с направлением силы.
Давайте посмотрим на небольшую иллюстрацию, чтобы понять, как найти тангенциальную скорость на изогнутой траектории. Мы рассматриваем пушечное ядро выстрелить с холма из пушки в тангенциальном направлении; когда тангенциальная скорость меньше угловой скорости, тангенциальная скорость будет меньше.
Формула тангенциальной скорости через центростремительная сила равна ac = −ω2r = ω × v. Здесь ac — центростремительное ускорение., r — радиус, ω — угловая скорость, v — тангенциальная скорость. Вот как найти тангенциальную скорость, соответствующую центростремительное ускорение.
«Пушечное ядро» by bitznbitez (ранее lucias_clay) под лицензией CC BY-NC-ND 2.0
Как найти тангенциальную скорость кругового движения?
Когда тело совершает круговое движение, определенные факторы будут способствовать этому движению. при круговом движении, как правило, необходимо учитывать тангенциальную величину veuewrhweiugr
Угловая скорость не рассматривается, так как не является линейной составляющей вращательного движения. Теперь тангенциальная скорость вращающегося тела при круговом движении будет действовать в направлении кругового движения.
Мы считаем центр этого движения источником кругового движения. Здесь тангенциальная скорость находится под прямым углом к радиусу.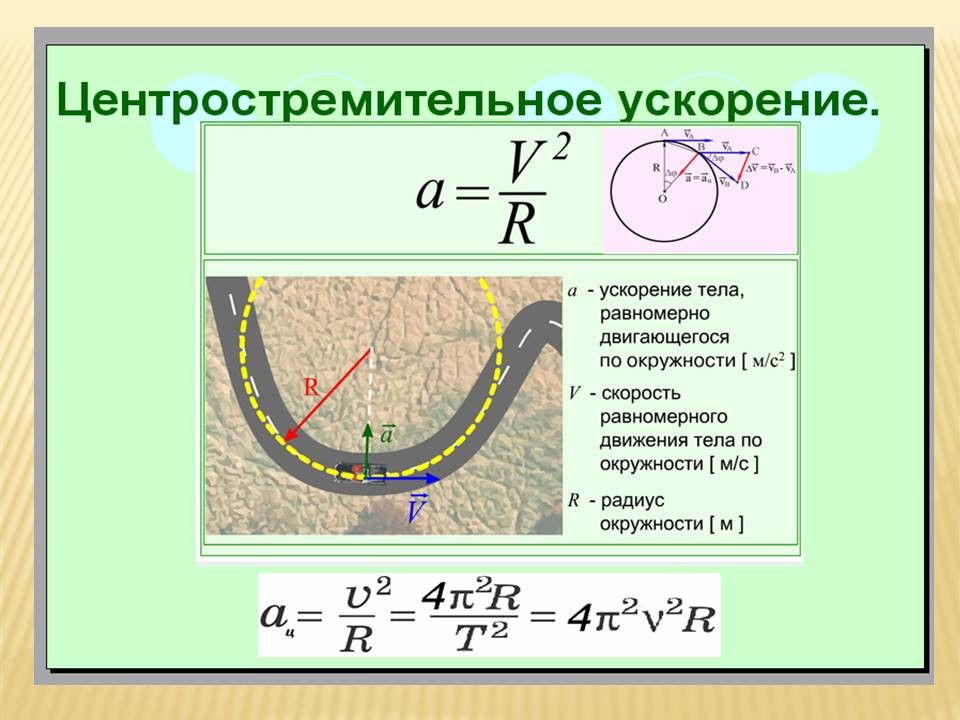
Кроме того, тангенциальная скорость входит в траекторию движущейся частицы.
Нет конкретной формулы для тангенциальная скорость в круговом движении, но одно общее использование типа формулы. Например, когда тело движется по круговой траектории, ему нужно сделать столько вращений, пока не завершится последний.
Когда это произойдет, нам нужно разделить длину окружности движения на количество раз, которое требуется для завершения этого вращения. Вот что говорит наука о круговом движении.
Как найти тангенциальную скорость без радиуса?
Линейная составляющая вращающегося тела при движении иногда измеряется и известна как тангенциальная скорость. Когда он действительно движется по круговой траектории, мы склонны сосредотачиваться на угловой скорости только потому, что это нелинейный компонент.
Термины тангенциальная скорость и линейная скорость означают одно и то же, когда мы рассматриваем движение как круговое.
Таким образом, нам не нужно запутаться в том, какой термин использовать в терминах кругового движения.
В одном измерении мы рассматриваем скорость, с которой тело приходит в прямое движение. Итак, нам нужно время и расстояние, чтобы определить скорость. Но когда мы рассматриваем круговое движение, также используется термин радиус.
Но иногда нельзя сказать, что вращательное движение всегда правильный круг, поэтому мы не можем выбрать радиус. Итак, вычисляя тангенциальная скорость без радиуса сложно, но можно определить.
Во-первых, нам необходимо рассмотреть вращательное движение быть несколько круглым. А затем попробуйте ввести его в круг, а затем найдите длина окружности этого конкретного. Теперь будет несколько раз, когда круговое движение завершится.
Нам нужно разделить окружность на количество раз, когда тело сделало вращение, чтобы завершить круговое движение. Тогда легче найти тангенциальную скорость, не вводя понятие радиуса.
Как найти тангенциальную скорость с угловой скоростью?
Это можно объяснить, используя иллюстрацию с использованием колеса. Поэтому поместите табличку с буквой K в центре, а другую — на краю. При быстром вращении колеса буква К в центре будет видна, а на ободе она не четкая.
Мы вычисляем угловую скорость колеса, когда заданный угол изменяется с заданным временем. Другой способ определения вращающегося объекта — использование понятия тангенциальной скорости.
Тангенциальная скорость — это точка на вращающемся объекте, расходящаяся в направлении движения по круговой траектории. Расстояние до точки на колесе в данный момент времени позволяет вычислить тангенциальную скорость вращающегося объекта.
В случае вращающегося объекта тангенциальная скорость увеличиваются, когда точка находится дальше от оси вращения. Точка на колесе должна двигаться быстрее, чем точка на оси вращения, потому что обе точки должны двигаться под определенным углом, чтобы соответствовать скорости друг друга.
Формула, связывающая угловую и тангенциальную скорости: Vt = rx ω. Радиус — это общий коэффициент, связывающий как линейную, так и угловую скорости.
«Умное автомобильное колесо» by Mr.TinDC под лицензией CC BY-ND 2.0
Как найти тангенциальную скорость с ускорением?
Тангенциальная скорость — это линейная составляющая вращающегося тела. Таким образом, ускорение также будет угловым, поскольку движение происходит по круговой траектории. Vt = rx ω — формула тангенциальной скорости, а ускорение — а = гх а.
При изменении угловой скорости в действие вступает угловое ускорение. Когда точка объекта, движущегося по круговой траектории, находится дальше от оси вращения, тангенциальная скорость увеличивается.
Когда объект непрерывно вращается, он подвергается угловое ускорение и тангенциальное ускорение или линейное ускорение.
“Веселье на детской площадке” Маркус Списке находится под лицензией CC0 1.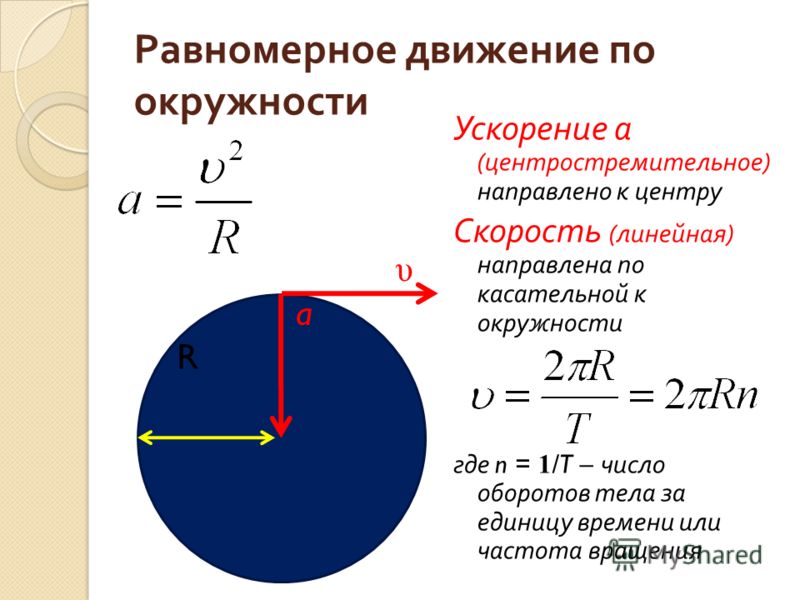
0
Мы можем рассмотреть пример карусели, в которой будут возникать угловые и линейные ускорения и сформировать, что линейная или тангенциальная скорость может быть вычислена.
Формула окружной скорости — GeeksforGeeks
Улучшить статью
Сохранить статью
При изменении скорости изменяется и ускорение, но не в том же направлении. В результате объект, движущийся по круговой траектории, всегда должен иметь ускорение, перпендикулярное скорости. Круговое движение может быть как равномерным, так и неравномерным. Формула равномерного кругового движения будет обсуждаться с примерами в этом разделе. Осваиваем эту тему!
Что такое окружная скорость?
Круговая скорость определяется как скорость, которой обладает объект при равномерном круговом движении. Равномерное круговое движение — это двумерное движение, при котором объект движется по кругу с постоянной скоростью, а скорость изменяется в каждом месте из-за изменения направления вектора скорости.
Круговая скорость прямо пропорциональна радиусу кругового пути, но обратно пропорциональна времени, которое проходит объект.
- Обозначается символом v c .
- Единицей измерения является м/с.
- И размерная формула дана [M 0 L 1 T -1 ].
Формула круговой скорости
Математически она определяется как длина окружности кругового пути, деленная на затраченное время.
v c = 2πr/T
где,
- v c — круговая скорость,
- r — радиус кругового пути,
- T — затраченное время.
Однако круговую скорость также можно рассчитать, если задана угловая скорость ω, и она рассчитывается как
v c = ω r
, r — радиус кругового пути
Примеры задач
Задача 1.
Вычислить круговую скорость объекта, совершающего круговое движение, если радиус равен 3 м за время 4 с.
Решение:
Мы имеем,
R = 3
T = 4
Используя формулу. )/4
= 18,84/4
= 4,71 м/с
Задача 2. Вычислить круговую скорость объекта, совершающего круговое движение, если радиус равен 5 м за время 2 с.
Решение:
У нас есть,
R = 5
T = 2
Используя формулу, которую мы имеем,
V C = 2πr/T
= (2 × 3,14 × 5)/2
= 31,4/2
= )/2
= 31,4/2
= )/2
= 31,4/2
= )/2
= 31,4/2
= )/2
= 31,4/2
9000 = )/ 15,7 м/с
Задача 3. Вычислить круговую скорость объекта, совершающего круговое движение, если радиус равен 4 м за время 7 с.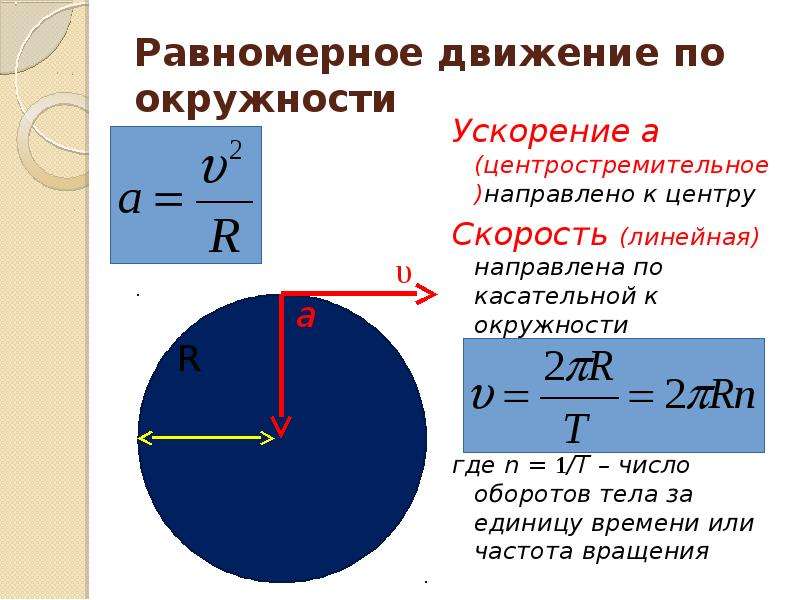
Решение:
Имеем,
r = 4
T = 7
Используя формулу имеем,
V C = 2πr/T
= (2 × 3,14 × 4)/7
= 25,12/7
= 3,58 м/с
Проблема 4: Вычисляйте. скорость тела, совершающего круговое движение, равна 5 м/с за время 3 с.
Solution:
We have,
v c = 5
T = 3
Using the formula we have,
v c = 2πr/T
=> r = v c T/2π
= (5 × 3)/(2 × 3,14)
= 15/6,28
= 2,38 м
Задача 5. Вычислить круговую скорость объекта, если совершает круговое движение со скоростью 8 м/с за время 2 с.
Solution:
We have,
v c = 8
T = 2
Using the formula we have,
v c = 2πr/T
=> r = в с T/2π
= (8 × 2)/(2 × 3,14)
= 16/6,28
= 2,54 м
скорость 7 м/с на радиусе 5 м.
Решение:
Мы имеем,
VC = 7
R = 5
Используя формулу,
V C = 2πr/T
9001 => T = 2πr/v/v = 2πr/v/v = 2πr/v C = 2πr/T
9000 => T = 2πr/v/v/v/v C = 2πr/T
9001 => T = 2πr/v C = 2πr/T
с
= (2 × 3,14 × 5)/7
= 31,4/7
= 4,48 с
Задача 7. Вычислить время, если круговая скорость объекта, совершающего круговое движение, равна 12 м/с для радиуса 8 м.
Solution:
We have,
v c = 12
r = 8
Using the formula we have,
v c = 2πr/T
=> T = 2πr/v c
= (2 × 3,14 × 8)/12
= 50,24/12
= 4,18 с
Наборы задач по круговому движению и гравитации
Наборы задач || Обзор физики || Устаревший набор задач
У нас есть 18 готовых наборов задач по теме Круговое движение и Гравитация.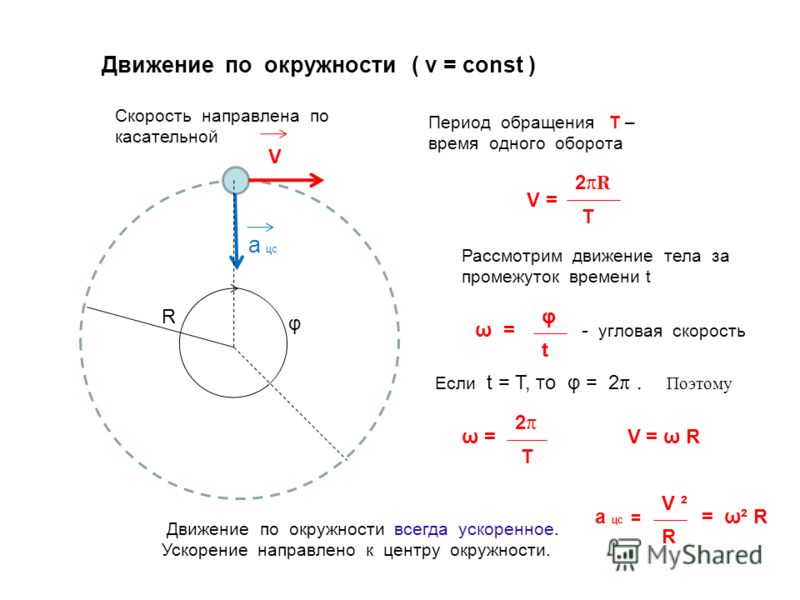
Эти наборы задач сосредоточены на использовании законов движения Ньютона и всемирного тяготения для математического анализа ситуаций, связанных с круговым движением или движением спутника.
Щелкните ссылку, чтобы открыть общедоступный набор задач. Если вы являетесь студентом системы отслеживания задач, откройте задание по ссылке на доске заданий системы отслеживания задач.
Набор задач CG1: Линейная скорость
Используйте уравнение v = 2•π•R/T для определения скорости, радиуса или периода. Включает 4 задачи.
Набор задач CG2: Центростремительное ускорение 1
Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение с радиусом окружности и периодом. Включает 7 задач.
Набор задач CG3: Центростремительное ускорение 2
Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение со скоростью вращения.
Включает 7 задач.
Набор задач CG4: Центростремительная сила
Используйте уравнения кругового движения, чтобы связать линейную скорость или центростремительное ускорение с центростремительной силой. Включает 5 задач.
Набор задач CG5: Круговое движение и анализ силы 1
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по вертикальным окружностям. Большинство проблем включают в себя строительные леса. Включает 7 задач.
Набор задач CG6: круговое движение и анализ силы 2
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по горизонтальным кругам. Включает 5 задач.
Набор задач CG7: круговое движение и анализ силы 3
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по кругу.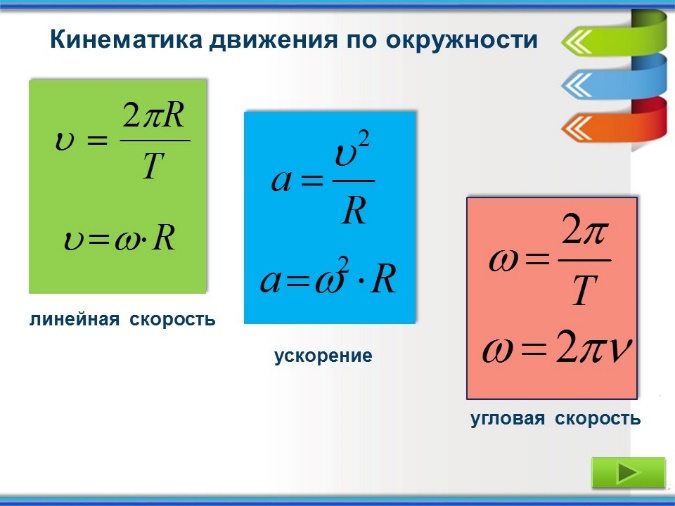
Включает 7 задач.
Набор задач CG8: круговое движение и анализ силы 4
Используйте уравнения кругового движения, анализ силы и второй закон Ньютона для анализа ситуаций с объектами, движущимися по кругу. Включает 7 задач.
Набор задач CG9: Гравитационная сила 1
Используйте закон всемирного тяготения Ньютона для расчета силы притяжения между двумя объектами с известной массой и расстоянием между ними. Включает 7 задач.
Набор задач CG10: Гравитационная сила 2
Используйте закон всемирного тяготения Ньютона для расчета силы притяжения между двумя объектами с известной массой и расстоянием между ними. Включает 5 задач.
Набор задач CG11: Гравитационная сила 3
Используйте закон всемирного тяготения Ньютона в качестве пропорционального аргумента и в качестве инструмента решения проблем для некоторых сложных сценариев.
Включает 4 задачи.
Набор задач CG12: Напряженность гравитационного поля
Используйте уравнение для напряженности гравитационного поля, чтобы вычислить значение g при различных условиях. Включает 6 задач.
Набор задач CG13: Орбитальная скорость
Используйте уравнение для орбитальной скорости, чтобы связать радиус орбиты, период обращения и массу центрального тела. Включает 8 задач.
Набор задач CG14: Орбитальное ускорение
Свяжите орбитальный период и орбитальный радиус с орбитальным ускорением. Включает 6 задач.
Набор задач CG15: Математика движения спутников
Используйте уравнения орбитального движения, чтобы связать радиус орбиты, орбитальную скорость, период обращения и массу центрального тела.