Длина волны — формулы, измерение, определение

Морские волны — далеко не все примеры волн. И длина волны — это не серферская характеристика, а вполне себе физическая величина. Сегодня разберемся, что такое волна и как ее охарактеризовать.

Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

• Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.

Электромагнитные волны — это те волны, которые мы потрогать не можем.

• Например, радиоволны, Wi-Fi и свет.

Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10⁸ м/с. И источники у них разные.

Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

• Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

• Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
• Видимый свет и дрожание гитарной струны — тоже поперечные волны.

Морская волна — продольная или поперечная?

На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

• λ — длина волны [м]

Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).

Переходя к волнам, можно провести следующие аналогии:

• путь — длина волны
• время — период

А для скорости даже аналогия не нужна — скорость и в Африке скорость.

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

1. Возьмем формулу скорости:

𝑣 = λ/T

2. Нам известна длина волны, но не дан период. Период вычисляется по формуле:

T = t/N

T = 40/10 = 4 с

3. Теперь подставляем величины в формулу

𝑣 = λ/T

𝑣 = ¼ = 0,25 м/с

Ответ: 𝑣 = 0,25 м/с

Резонанс

Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Глава 7. Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах

Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине

Силу (7. 6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7. 5). Имеем

(правильный ответ – 2).

Применяя определение угловой скорости к колесу (задача 7.1.3), получаем

(правильный ответ 1).

Из формулы (7.2) имеем

(задача 7.1.4 – правильный ответ 4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска

А теперь по формуле (7.5) для второй точки получаем

(ответ 2).

Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7. 4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно

(ответ 4).

Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с², получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1

(ответ 1).

Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем

(ответ 3).

Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим

Поэтому

(ответ 1).

Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)

где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем

(ответ 2).

Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения

Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства

(ответ 4).

В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем

(ответ 3).

В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает

На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем

Подставляя в эту формулу силу из формулы (1), находим (ответ 2).

В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем

где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим

(ответ 3).

Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):

где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно

(задача 7. 2.9 – ответ 1).

Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).

Период и частота — макеты

Авторы: Стивен Хольцнер и

Обновлено: 26 марта 2016 г.

Онлайн-практика

Исследуйте книгу Купить на Amazon

При описании того, как все идет по кругу, вы не просто используете радианы; Вы также можете указать время, которое требуется. Время, за которое объект совершает полный оборот, называется период его движения. Обычно период измеряется в секундах, но его можно измерять и в других единицах времени, включая миллисекунды, минуты и годы.

Если объект движется со скоростью v , , то время, необходимое для прохождения круга — расстояние, которое он проходит по окружности, 2π r — будет

Обратите внимание на символ радиуса окружности: r .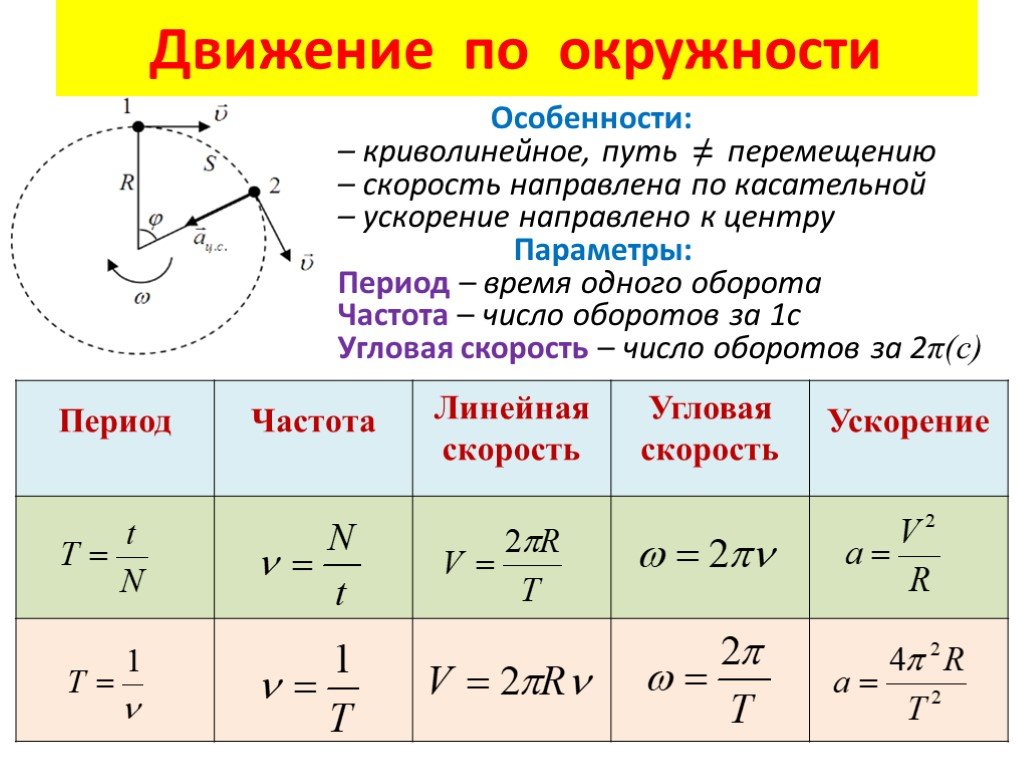 Это половина диаметра круга, который равен 9.0019 д . Итак, r = d /2. Обратите также внимание на символ периода: T . С помощью этого уравнения, учитывая скорость объекта на орбите и радиус окружности, вы можете рассчитать период объекта.

Другим измерением, которое вы встретите в задачах по физике, является частота . В то время как период — это время, за которое объект совершает круг, частота — это количество кругов, которые объект делает за единицу времени. Частота, f , подключается к периоду так:

Частота чаще всего измеряется в единицах циклов в секунду (cps), которые также называются Герцами (Гц). Объект, движущийся по кругу с частотой 2,0 Гц, каждую секунду совершает два оборота по кругу.

Пример вопроса

1. Радиус орбиты Луны составляет 3,85 x 10 ⁸ м, а ее период составляет около 27,3 дня. Какова его скорость при движении вокруг Земли?

   Правильный ответ: 1020 м/с при округлении до значащих цифр.

   1. Преобразовать 27,3 дня в секунды:

   2. Используйте уравнение для периода, чтобы найти скорость:

   3. Подставьте числа:

Практические вопросы

1. У вас есть мяч на веревке, и вы крутите его по кругу. Какова его скорость, если радиус его окружности равен 1,0 м, а его период равен 1,0 с?

2. У вас есть игрушечный самолетик на проводе, и он летит по кругу. Какова его скорость, если радиус его окружности равен 10,0 м, а его период равен 0,75 с?

Ниже приведены ответы на практические вопросы:

1. 6,3 м/с

   1. Используйте уравнение для периода, чтобы найти скорость:

   2. Подставьте числа:

2. 84 м/с

   1. Используйте уравнение для периода, чтобы найти скорость:

   2. Подставьте числа:

Об этой статье

Эта статья из книги:

• Рабочая тетрадь по физике I для чайников с онлайн-практикой,

Об авторе книги:

Эту статью можно найти в категории:

0

3

8 Физика, Как рассчитать период движения в физике

Мир природы полон примеров периодического движения: от орбит планет вокруг Солнца до электромагнитных колебаний фотонов и биения нашего собственного сердца.

Все эти колебания связаны с завершением цикла, будь то возвращение тела на орбиту в исходную точку, возвращение вибрирующей пружины в точку равновесия или расширение и сокращение сердцебиения. Время, необходимое колебательной системе для завершения цикла, известно как период .

Период системы — это мера времени, и в физике он обычно обозначается заглавной буквой ​ T ​. Период измеряется в единицах времени, соответствующих данной системе, но чаще всего используются секунды. Секунда — это единица времени, первоначально основанная на вращении Земли вокруг своей оси и на ее орбите вокруг Солнца, хотя современное определение основано на колебаниях атома цезия-133, а не на каком-либо астрономическом явлении.

Периоды некоторых систем интуитивно понятны, например, вращение Земли, равное дню, или (по определению) 86 400 секунд. Вы можете рассчитать периоды некоторых других систем, таких как колеблющаяся пружина, используя характеристики системы, такие как масса и жесткость пружины.

Когда дело доходит до колебаний света, все становится немного сложнее, потому что фотоны движутся в поперечном пространстве, пока они вибрируют, поэтому длина волны является более полезной величиной, чем период.

Период обратно пропорционален частоте

Период – это время, необходимое колебательной системе для завершения цикла, тогда как ​ частота (​ f ​) ​ – это количество циклов, которое система может совершить завершить в заданный период времени. Например, Земля вращается один раз в сутки, поэтому период равен 1 дню, а частота также равна 1 обороту в сутки. Если вы установите стандарт времени на годы, период составит 1/365 года, а частота — 365 циклов в год. Период и частота являются обратными величинами:

T = \frac{1}{f}

В расчетах, связанных с атомными и электромагнитными явлениями, частота в физике обычно измеряется в циклах в секунду, также называемых Герцами (Гц), с ⁻¹ или 1/сек.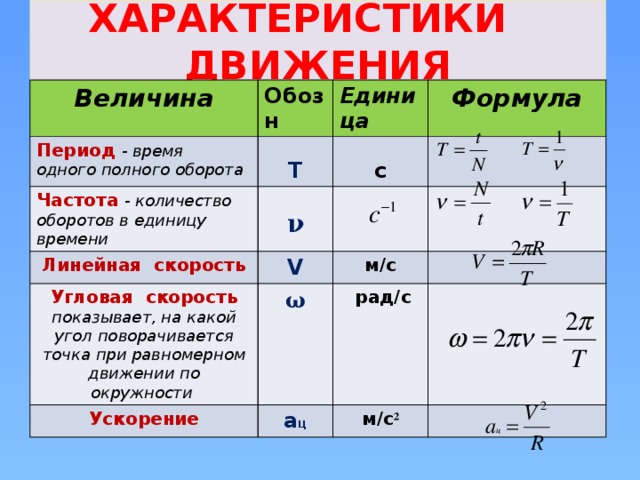 . При рассмотрении вращающихся тел в макроскопическом мире число оборотов в минуту (об/мин) также является общепринятой единицей. Период может измеряться в секундах, минутах или любом другом подходящем периоде времени.

Период простого гармонического осциллятора

Самым основным типом периодического движения является движение простого гармонического осциллятора, который определяется как движение, которое всегда испытывает ускорение, пропорциональное его расстоянию от положения равновесия и направленное к равновесию должность. В отсутствие сил трения и маятник, и груз, прикрепленный к пружине, могут быть простыми гармоническими осцилляторами.

Колебания массы на пружине или маятнике можно сравнить с движением тела, вращающегося с равномерным движением по круговой траектории с радиусом ​ r ​. Если угловая скорость тела, движущегося по окружности, равна ω, его угловое смещение ( θ ) от начальной точки в любой момент времени t равно θ ​ = ωt ​, и компоненты его положения x и y равны x = r ​ cos(​ ωt ​) и ​ y ​ = ​ r ​ sin(​ ωt ​).

Многие осцилляторы движутся только в одном измерении, и если они движутся горизонтально, то движутся в направлении ​ x ​. Если амплитуда, которая дальше всего отходит от положения равновесия, равна A , то положение в любой момент времени t равно x = A cos( ωt ​). Здесь ω известна как угловая частота и связана с частотой колебаний ( f ​) уравнением ​ ω ​ = 2π​ f ​. Поскольку ​ f ​ = 1/​ T ​, период колебаний можно записать так:

T = \frac{2π}{ω}

Пружины и маятники: уравнения периода по закону Гука на пружину действует восстанавливающая сила F = − k x , где k — характеристика пружины, известная как жесткость пружины, а x — рабочий объем. Знак минус указывает, что сила всегда направлена ​​против направления смещения. Согласно второму закону Ньютона, эта сила также равна массе тела ( m ), умноженной на его ускорение ( a ), поэтому ma = − kx .

Для объекта, колеблющегося с угловой частотой ω , ускорение равно − Aω ² cos ωt или, упрощенно, − ω ² x . Теперь вы можете написать ​ м ​( −​ ω ​ ² ​ x ​) = −​ kx ​, удалить x и получить ​ к ​/​ м ​). Тогда период колебаний массы на пружине равен:

T = 2π\sqrt{\frac{m}{k}}

Аналогичные рассуждения можно применить к простому маятнику, на котором вся масса центрируется на конце строки. Если длина строки равна L ​, уравнение периода в физике для малоуглового маятника (т.е. такого, в котором максимальное угловое смещение от положения равновесия мало), которое оказывается не зависящим от массы, равно

T = 2π\sqrt{ \frac{L}{g}}

где ​ g ​ — ускорение свободного падения.

Период и длина волны волны

Подобно простому осциллятору, волна имеет точку равновесия и максимальную амплитуду по обе стороны от точки равновесия. Однако, поскольку волна распространяется через среду или пространство, колебания растягиваются вдоль направления движения. Длина волны определяется как поперечное расстояние между любыми двумя одинаковыми точками цикла колебаний, обычно точками максимальной амплитуды по одну сторону от положения равновесия.

Период волны — это время, за которое одна полная длина волны проходит контрольную точку, тогда как частота волны — это количество длин волн, которые проходят через контрольную точку за заданный период времени. Когда период времени равен одной секунде, частота может быть выражена в циклах в секунду (Герцах), а период выражен в секундах.

Период волны зависит от скорости ее движения и длины волны (​ λ ​). Волна проходит расстояние в одну длину волны за один период, поэтому формула скорости волны равна 9.0153 v ​ = ​ λ ​/​ T ​, где ​ v ​ — скорость. Выразив период через другие величины, вы получите:

T = \frac{λ}{v}

Например, если волны на озере разделены 10 футами и движутся со скоростью 5 футов в секунду, период каждой волны 10/5 = 2 секунды.