Содержание
Угловая скорость. Формула угловой скорости :: SYL.ru
Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие – скорость. И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч — значит за один час проехать 100 километров.
А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды – Солнца — делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!
Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?
Понятие угловой скорости
Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).
Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» — ω.
Классическая формула угловой скорости вращения рассматривается так.
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.
Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:
∆t = t2 – t1.
Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:
∆φ = φ2 – φ1.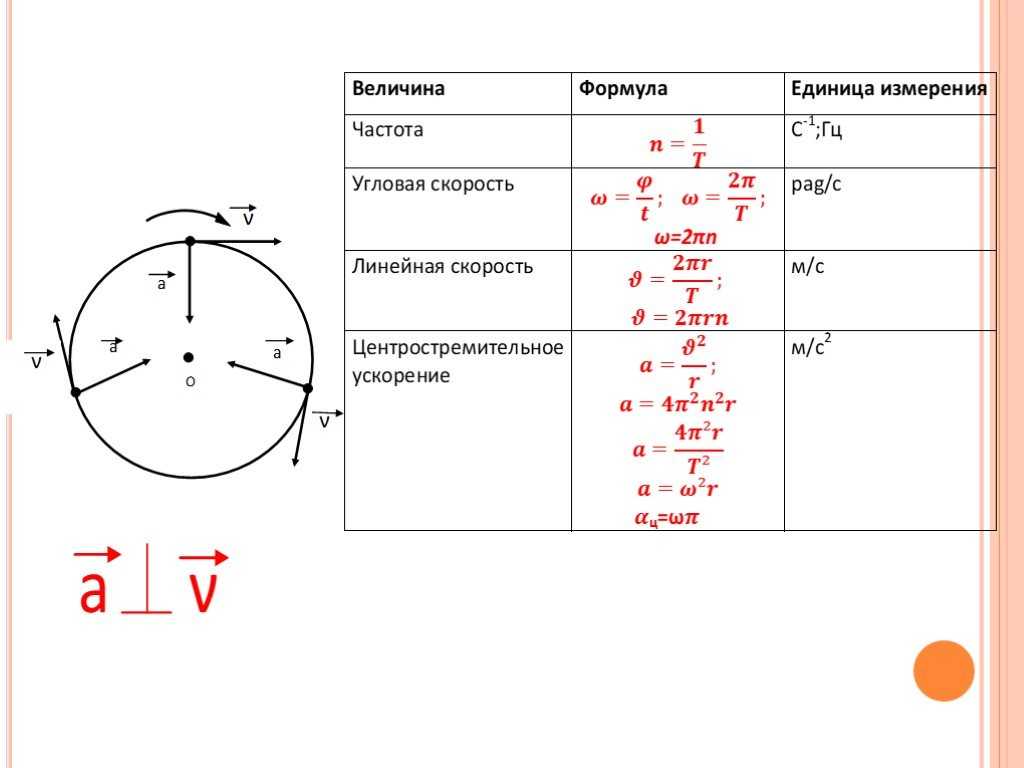
Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.
Единицы измерения угловой скорости
Скорость движения тела линейная измеряется в разных величинах. Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы – морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.
Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.
Радианы в секунду (рад/с) – классическое мерило скорости в международной системе единиц (СИ). Показывают – на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.
Обороты в минуту (об/мин) – самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.
Обороты в секунду (об/с) – используется реже, прежде всего в образовательных целях.
Период обращения
Иногда для определения скорости вращения удобнее пользоваться другим понятием. Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:
ω = 2П / Т.
Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.
Формула угловой скорости позволяет вычислить её, зная период обращения:
ω = 2П/31536000 = 0,000000199238499086111 рад/с.
Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.
Связь угловой и линейной скоростей
В некоторых задачах должны быть определены линейная и угловая скорость.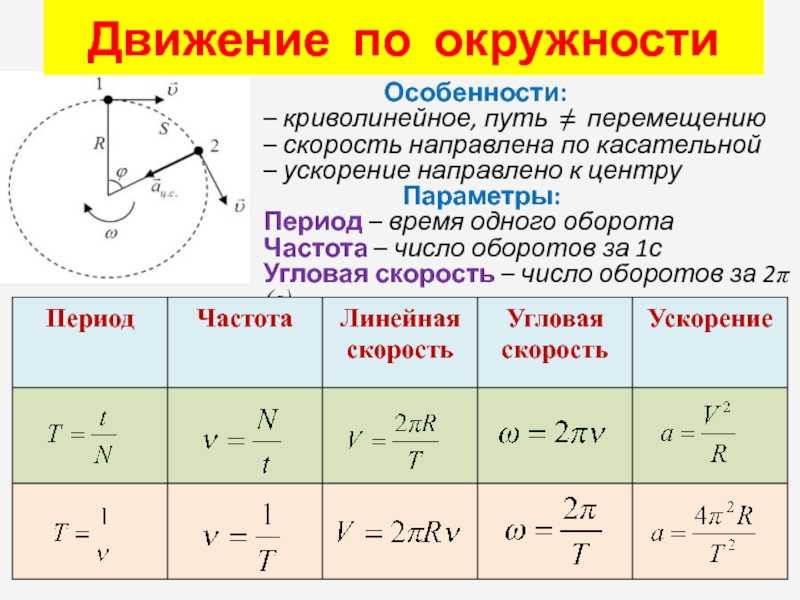 Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.
Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.
«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.
Что это — угловая скорость и как ее рассчитывают?
Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а угловая скорость. Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.
Угловая скорость: понятие и формула
Когда материальная точка движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности.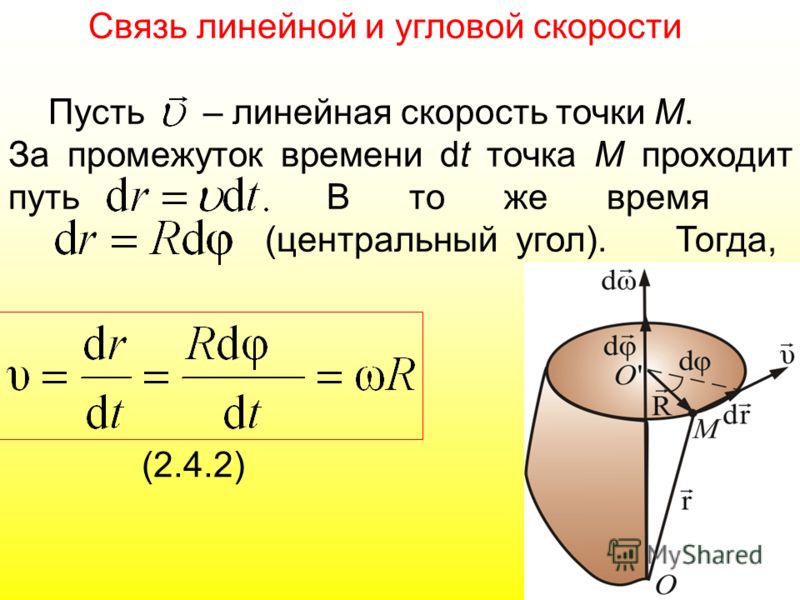 Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:
Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:
w = φ / t, где:
φ – угол поворота радиуса,
t – период времени вращения.
Единицы измерения величины
В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с – основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):
w = 2π*n,
где n – частота вращения.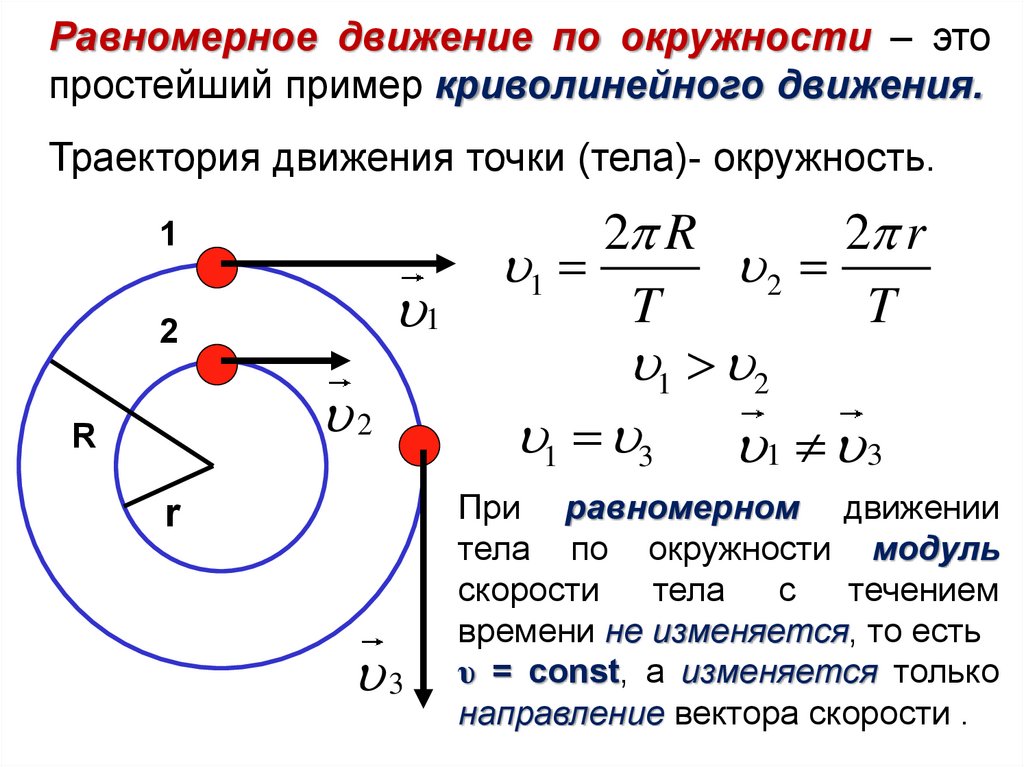
В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют правило буравчика, которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит поступательное движение винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.
Примеры расчета
Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:
w = φ / t = 7t / t = 7 с-1.
Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t.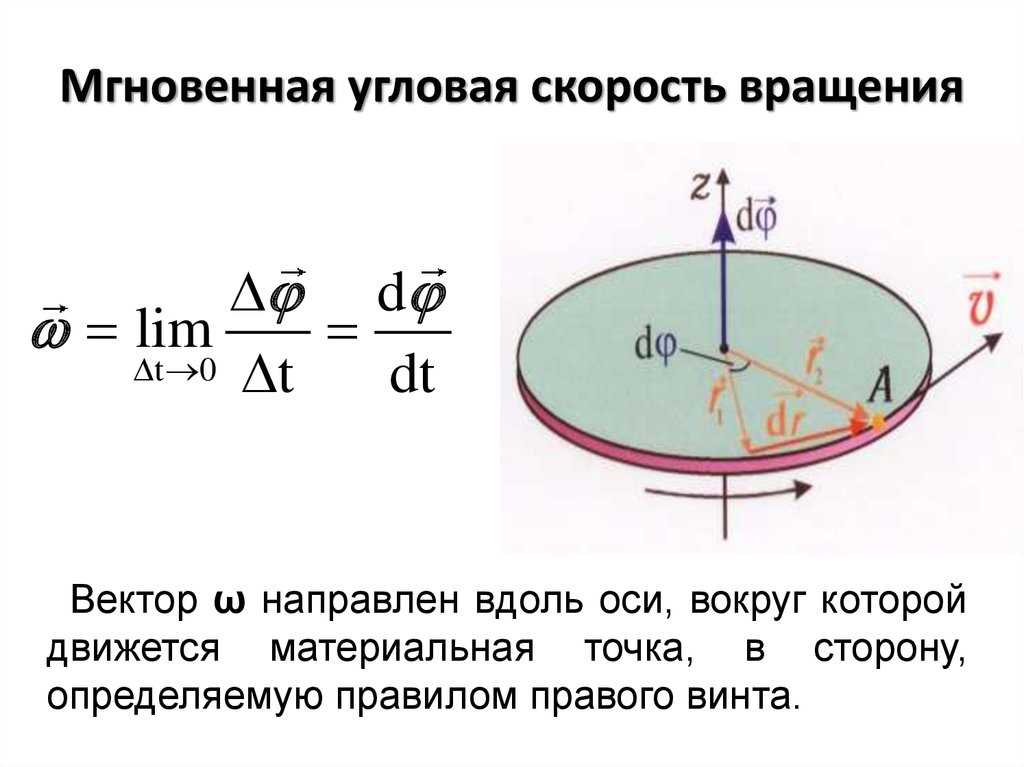 Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π — один полный оборот, получается следующее:
Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π — один полный оборот, получается следующее:
v = 2π*r / t = w * r = 7 * 0.5 = 3.5 м/с
Вот еще одна задачка на эту тему. Известно, что радиус Земли на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:
w = 2π*n = 2*3,14 *(1/(2 3600)) = 7,268 *10-5 рад/с.
Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10-5 *6370 * 1000 = 463 м/с.
1.4: Скорость и угловая скорость
-
- Последнее обновление
- Сохранить как PDF
-
- Идентификатор страницы
- 7100
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
- Что такое длина дуги?
- В чем разница между линейной скоростью и угловой скоростью?
- Какие формулы связывают линейную скорость с угловой скоростью?
- Какова формула длины окружности \(C\) круга, радиус которого равен \(r\)?
- Предположим, что человек \(A\) идет по окружности круга радиусом 10 футов, а человек B идет по окружности круга радиусом 20 футов. Кроме того, предположим, что обоим \(A\) и \(B\) требуется 1 минута, чтобы пройти четверть окружности их соответствующих кругов (четверть полного оборота). Кто прошел наибольшее расстояние?
- Предположим, что оба человека продолжают идти с той же скоростью, что и в первую минуту. Сколько полных оборотов по кругу совершит каждый человек за 8 минут? Через 10 минут?
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 10 футов, которая тянется центральный угол \(\dfrac{\pi}{2}\) радиан. Результат равен одной четверти длины окружности?
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 20 футов, которая образует центральный угол \(\dfrac{\pi}{2}\) радиан.
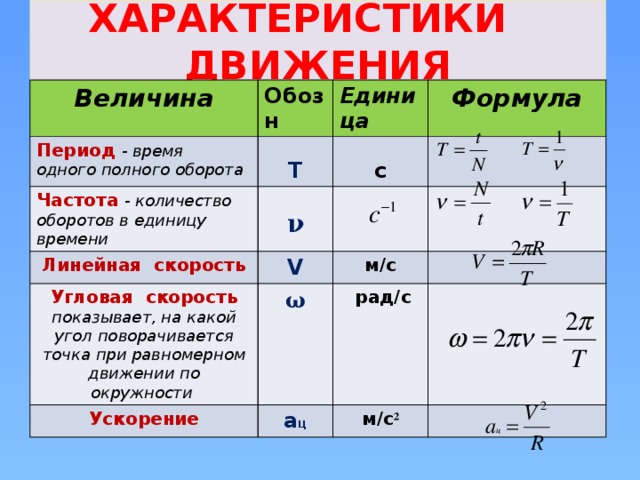 Результат равен одной четверти длины окружности? 9\circ}) = \dfrac{11\pi}{90}\), и \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11 \pi}{30}\] Длина дуги составляет \(\dfrac{11\pi}{30}\) футов или около \(1,1519\) футов.
Результат равен одной четверти длины окружности? 9\circ}) = \dfrac{11\pi}{90}\), и \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11 \pi}{30}\] Длина дуги составляет \(\dfrac{11\pi}{30}\) футов или около \(1,1519\) футов. - Определите угловую скорость \(\omega\) точки в радианах в минуту. Подсказка : Используйте формулу \[\omega = x \dfrac{об} {мин} \cdot \dfrac{2\pi rad}{об}.\]
- Теперь мы знаем \(\omega = \dfrac{\theta}{t}\). Поэтому используйте формулу \(v = \dfrac{r\theta}{t}\), чтобы определить \(v\) в футах в минуту.
- Наконец, преобразуйте линейную скорость v в футах в минуту в футы в секунду.
- Ответить
-
1. Мы видим, что
\[\omega = 40\dfrac{об} {мин} \times \dfrac{2\pi\space рад}{об}\]
\[\omega = 80\pi\dfrac{rad}{мин}\ ]2. Результат пункта (а) дает
\[v = r(\dfrac{\theta}{r}) = r\omega\]
\[v = (3ft) \times 80\pi\dfrac{rad}{min}\]
\[v = 240\pi\dfrac{ft}{мин}\]3.
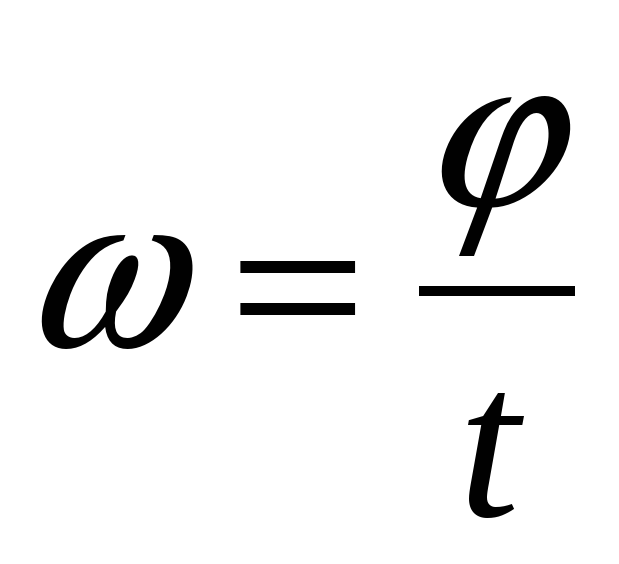 Теперь мы конвертируем футы в минуту в футы в секунду.
Теперь мы конвертируем футы в минуту в футы в секунду.\[v = 240\pi\dfrac{ft}{min} \times \dfrac{1\space min}{60\space sec}\]
\[v = 4\pi\dfrac{ft}{sec} \приблизительно 12,566\dfrac{ft}{sec}\] - Земля совершает оборот вокруг своей оси каждые \(24\) часа. Определить угловую скорость Земли в радианах в час. (Оставьте свой ответ в терминах числа ��\(\pi\).) 9\circ\) на север будет двигаться по кругу радиусом 2800 миль. Определите линейную скорость этого человека в милях в час и футах в секунду.
- Ответить
-
- Один оборот соответствует \(2\pi\) радианам. Итак, \[\omega = \dfrac{2\pi\space rad}{24\space hr} = \dfrac{\pi\space rad}{12\space hr}.
 \]
\] - Для определения линейной скорости используем формулу \(v = r\omega\) \[v = r\omega = (3959mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{3959\pi}{12}\dfrac{mi}{hr}\] Линейная скорость составляет примерно 1036,5 миль в час.
- Для определения линейной скорости используем формулу \(v = r\omega\) \[v = r\omega = (2800mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{2800\pi}{12}\dfrac{mi}{hr}\] Линейная скорость составляет примерно 733,04 мили в час. Чтобы преобразовать это в футы в секунду, мы используем тот факт, что в одной миле 5280 футов, в часе 60 минут, а в минуте 60 секунд. Итак,
\[v = (\dfrac{2800\pi}{12}\dfrac{mi}{hr})(\dfrac{5280\space ft}{1\space mi})(\dfrac{1\space hr }{60\пробел мин})(\dfrac{1\пробел мин}{60\пробел сек}) = \dfrac{(2800\pi)(5280)}{12\cdot 60\cdot 60}\dfrac{ft {сек}\]
Таким образом, линейная скорость составляет приблизительно \(1075,1\) футов в секунду.
- Один оборот соответствует \(2\pi\) радианам. Итак, \[\omega = \dfrac{2\pi\space rad}{24\space hr} = \dfrac{\pi\space rad}{12\space hr}.
- На окружности радиуса \(r\) длина дуги \(s\), пересекаемая центральным углом с мера радиана равна \[s = r\theta\]
- Равномерное круговое движение — это когда точка движется с постоянной скоростью по окружности.
 линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки представляет собой меру угла в радианах, деленную на время, которое требуется, чтобы выметать этот угол.
линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки представляет собой меру угла в радианах, деленную на время, которое требуется, чтобы выметать этот угол. - Для точки \(P\), движущейся с постоянной (линейной) скоростью v по окружности окружности радиуса \(r\), имеем \[v = r\omega\], где \(\omega\) есть угловая скорость точки.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
-
- Теги
-
- угловая скорость
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12 - скорость
-
Луна обращается вокруг Земли примерно за 27,3 дня. Какова его угловая скорость?
Правильный ответ: 2,66 x 10 –6 радиан/с.

-
Преобразовать 27,3 дня в секунды:
-
Используйте уравнение для угловой скорости:
-
Подставьте числа:
-
-
У вас есть игрушечный самолет на веревке, которая делает три полных круга за 9.0 с. Какова его угловая скорость?
-
Вы размахиваете бейсбольной битой, готовясь к удару по мячу. Если летучей мышью сделать полукруг за 1,0 с, какова будет ее угловая скорость?
-
Спутник вращается вокруг Земли со скоростью 8,7 x 10 –4 радиан/с. Сколько времени потребуется, чтобы обогнуть весь мир?
-
Карусель вращается со скоростью 2,1 радиан/с. Сколько времени потребуется, чтобы пройти полный круг?
-
(2/3)ð радиан/с (2,1 радиан/с)
-
Используйте уравнение для угловой скорости:
-
Подставьте числа:
-
-
ð радиан/с (3,1 радиан/с)
-
Используйте уравнение для угловой скорости:
-
2.

-
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Начальное занятие
Длина дуги на окружности
В разделе 1. 3 мы узнали, что мера угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Будут времена, когда также будет полезно знать длину дуг на других окружностях, которые опираются на тот же самый угол.
3 мы узнали, что мера угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Будут времена, когда также будет полезно знать длину дуг на других окружностях, которые опираются на тот же самый угол.
Рисунок \(\PageIndex{1}\): Дуги, опирающиеся на угол в 1 радиан.
На рисунке \(\PageIndex{1}\) внутренний круг имеет радиус 1, внешний круг имеет радиус \(r\), а показанный угол имеет меру \(\theta\ ) радианы. Таким образом, длина дуги на единичной окружности, опирающейся на угол, равна \(\theta\), и мы использовали s для представления длины дуги на окружности радиуса \(r\), опирающейся на угол.
Напомним, что длина окружности радиуса \(r\) равна \(2\pi r\), а длина окружности радиуса 1 равна \(2\pi\). Следовательно, отношение длины дуги \(s\) на окружности радиуса \(r\), которая образует угол \(\тета\) радиан, к соответствующей дуге на единичной окружности, равно \(\dfrac{2 \pi r}{2\pi} = r\). Отсюда следует, что
Отсюда следует, что
\[\dfrac{s}{\theta} = \dfrac{2\pi r}{\pi}\]
\[s = r\theta\]
Определение
На окружности радиуса \ (r\), длина дуги s, пересекаемая центральным углом в радианах, равна
\[s = r\theta\]
Примечание
Важно помнить, что для вычисления длины дуги мы должны измерить центральную угол в радианах.
(Непонятно, почему буква \(s\) обычно используется для обозначения длины дуги. Одно из объяснений состоит в том, что дуга «стягивает» угол.)
Упражнение \(\PageIndex{1}\)
Использование окружностей в начальном упражнении для этого раздела:
Почему радианы?
Градусная мера привычна и удобна, так почему же мы вводим единицу измерения радиан? Это хороший вопрос, но с тонким ответом. Как мы только что видели, длина \(s\) дуги на окружности радиуса \(r\), опирающейся на угол \(\theta\) радиан, определяется выражением \(s = r\theta\), поэтому \(\тета = \dfrac{s}{r}\). В результате радиан представляет собой отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), а также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусную размерность в вычислениях. Это означает, что мера в радианах на самом деле более естественна с математической точки зрения, чем градусная мера.
Это означает, что мера в радианах на самом деле более естественна с математической точки зрения, чем градусная мера.
Линейная и угловая скорость
Связь между дугой на окружности и углом, который она образует, измеряемым в радианах, позволяет нам определять величины, связанные с движением по окружности. Объекты, движущиеся по круговым траекториям, обладают двумя типами скорости: линейной и угловой скоростью. Подумайте о вращении на карусели. Если вы уроните камешек с края движущейся карусели, камешек не упадет прямо вниз. Вместо этого он будет продолжать двигаться вперед со скоростью, которую карусель имела в момент выпуска камешка. Это линейная скорость камня. линейная скорость измеряет, как длина дуги изменяется во времени.
Рассмотрим точку \(P\), движущуюся с постоянной скоростью по окружности радиуса \(r\). Это называется равномерным круговым движением . Предположим, что P перемещается на расстояние s единиц за время \(t\). Линейная скорость v точки \(P\) равна пройденному ею расстоянию, деленному на прошедшее время. То есть \(v = \dfrac{s}{t}\). Расстояние s — это длина дуги, и мы знаем, что \(s = r\theta\).
Линейная скорость v точки \(P\) равна пройденному ею расстоянию, деленному на прошедшее время. То есть \(v = \dfrac{s}{t}\). Расстояние s — это длина дуги, и мы знаем, что \(s = r\theta\).
Определение: линейная скорость
Рассмотрим точку \(P\), движущуюся с постоянной скоростью по окружности радиуса \(r\). линейная скорость \(v\) точки \(P\) определяется выражением
\[v = \dfrac{s}{t} = \dfrac{r\theta}{t}\]
где \(\theta\), измеренный в радианах, представляет собой центральный угол, опирающийся на дугу длины \(s\).
Другой способ измерения скорости движения объекта с постоянной скоростью по круговой траектории называется угловой скоростью. В то время как линейная скорость измеряет, как длина дуги изменяется с течением времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол с течением времени.
Определение: угловая скорость
Рассмотрим точку P, движущуюся с постоянной скоростью по окружности радиуса r по дуге, соответствующей центральному углу измерения \(\theta\) (в радианах). Угловая скорость \(\omega\) точки равна отношению угла \(\theta\) в радианах к времени t, которое требуется, чтобы выметать этот угол. Это
Угловая скорость \(\omega\) точки равна отношению угла \(\theta\) в радианах к времени t, которое требуется, чтобы выметать этот угол. Это
\[\omega = \dfrac{\theta}{t}.\]
Примечание
Символ \(\omega\) — это строчная греческая буква «омега». Также обратите внимание, что угловая скорость не зависит от радиуса r.
Это несколько специальное определение угловой скорости, которое немного отличается от общего термина, используемого для описания скорости вращения точки по окружности. Этот термин равен оборотов в минуту или оборотов в минуту . Иногда используется единица оборотов в секунду . Лучший способ представить число оборотов в минуту — использовать «долю единицы измерения» \(\dfrac{rev}{min}\). Поскольку 1 оборот равен \(2\pi\) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то
\[\omega = x \dfrac{об} {мин} \cdot \dfrac{2\pi рад} {об} = x(2\pi)\dfrac {рад}{мин}. \]
\]
Упражнение \(\PageIndex{2}\)
Предположим, что круглый диск вращается со скоростью 40 оборотов в минуту. Мы хотим определить линейную скорость v (в футах в секунду) точки, которая находится в 3 футах от центра диска.
Обратите внимание, что в упражнении 1.18, как только мы определили угловую скорость, мы смогли определить и линейную скорость. То, что мы сделали в данном конкретном случае, мы можем сделать в целом. Существует простая формула, напрямую связывающая линейную скорость с угловой скоростью. Наша формула для линейной скорости: \(v =\dfrac{s}{t} \dfrac{r\theta}{t}\). Обратите внимание, что мы можем записать это как \(v = r\dfrac{\theta}{t}\). То есть \(v = r\omega\)
Примечание
Рассмотрим точку \(P\), движущуюся с постоянной (линейной) скоростью \(v\) по окружности радиуса \(r\). Если угловая скорость равна \(\omega\), то
\[v = r\omega\]
Итак, в упражнении 1.18, как только мы определили, что \(\omega = 80\pi \dfrac{rad}{min }\), мы могли бы определить v следующим образом:
\[v = r\omega = (3\space ft)(80\pi\dfrac{rad}{min} = 240\pi\dfrac{ft}{min }).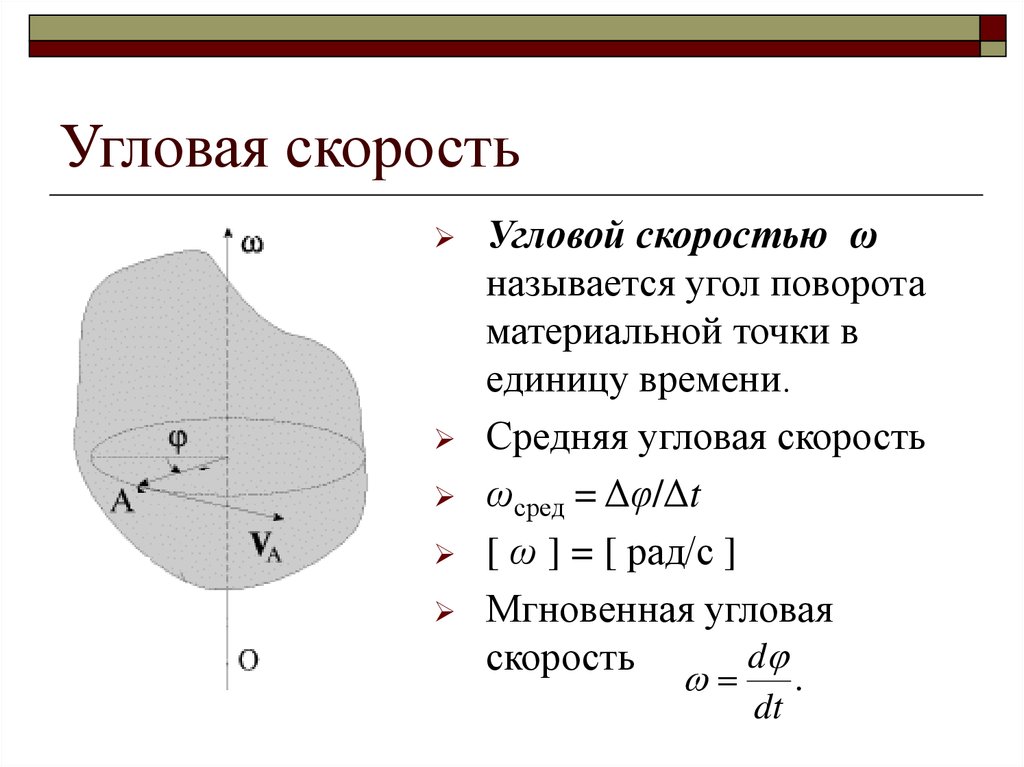 \]
\]
Обратите внимание, что, поскольку радианы «безразмерны», мы можем опускать их при работе с уравнениями, подобными предыдущему.
Пример \(\PageIndex{1}\): линейная и угловая скорость
LP (long play) или виниловая пластинка со скоростью вращения 331 об/мин представляет собой аналоговый носитель для хранения звука и долгое время использовался для прослушивания музыки. LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы преобразуем \(33\dfrac{1}{3}\) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \(33\dfrac{1}{3} = \dfrac{100}{3}\)
\[\omega = \dfrac{100}{3}\dfrac{об} {мин} \times \dfrac{2\pi \space rad}{1\space rev} = \dfrac{200\pi}{ 3}\dfrac{rad}{min}\]
Теперь мы можем использовать формулу v D r! для определения линейной скорости точки на краю 12-дюймового LP. Радиус равен 6 дюймов, поэтому
\[v = r\omega = (6\space дюймов)(\dfrac{200\pi}{3}\dfrac{rad}{min}) = 400\pi \dfrac{ дюймы}{мин}\]
Возможно, было бы удобнее выразить это как десятичное значение в дюймах в секунду. Итак, мы получаем
Итак, мы получаем
\[v = 400\pi \dfrac{дюймы}{мин} \times \dfrac{1\space min}{60 \space sec} \приблизительно 20,944\dfrac{дюймы}{sec}\]
Линейная скорость составляет примерно 20,944 дюйма в секунду.
Упражнение \(\PageIndex{3}\)
Для этих задач предположим, что Земля представляет собой сферу с радиусом 3959 миль. Поскольку Земля вращается вокруг своей оси, человек, стоящий на Земле, будет двигаться по кругу, перпендикулярному оси.
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
Эта страница под названием 1.4: Velocity and Angular Velocity распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Угловая скорость — манекены
Автор: Стивен Хольцнер и
Обновлено: 26-03-2016
Из книги: Рабочая тетрадь по физике I для чайников с онлайн-практикой
Рабочая тетрадь по физике I для чайников с онлайн-практикой
Книга-поиск Купить на Amazon
Существуют аналоги каждой величины линейного движения (например, расстояния, скорости, и ускорение) в угловом движении, и это одна из вещей, которая облегчает работу с угловым движением после того, как вы узнали о линейном движении. Скорость объекта в линейном движении показана в следующем уравнении (на самом деле это векторное уравнение, конечно, но вы можете посмотреть на это уравнение в скалярном выражении):
Какой аналог этого уравнения в угловых единицах? Это просто; вы просто подставляете расстояние под углом тета, поэтому угловая скорость равна тета/ t . Это означает, что угловая скорость — это угол (в радианах), который объект проходит за секунду. Символ угловой скорости — омега, поэтому вы можете написать уравнение для угловой скорости следующим образом:
Это означает, что угловая скорость — это угол (в радианах), который объект проходит за секунду. Символ угловой скорости — омега, поэтому вы можете написать уравнение для угловой скорости следующим образом:
На рисунке показана линия, описывающая окружность. В определенный момент она находится под углом тета, и если на это требуется время t , чтобы добраться туда, его угловая скорость равна омега = тета/ t .
Итак, если линия совершает полный оборот за 1,0 с, ее угловая скорость равна 2π/1,0 с = 2π радиан/с (поскольку в полном круге 2π радиан). С технической точки зрения радиан не является физической единицей измерения (это отношение), поэтому угловую скорость также можно записать как 2π с –1 .
Зная угловую скорость, вы также можете найти угол, пройденный за количество секунд:
Пример вопроса
Практические вопросы
Ниже приведены ответы на практические вопросы: