Содержание
Что такое угловая скорость простыми словами?
Что такое угловая скорость простыми словами?
В системе СИ угол поворота измеряется в радианах (рад). Угловой скоростью называется величина, характеризующая быстроту вращения твердого тела, равная отношению элементарного угла поворота dφ к промежутку времени dt, за Page 5 5 который произошел этот поворот, или первой производной угла поворота по времени.
Как найти скорость через угловую скорость?
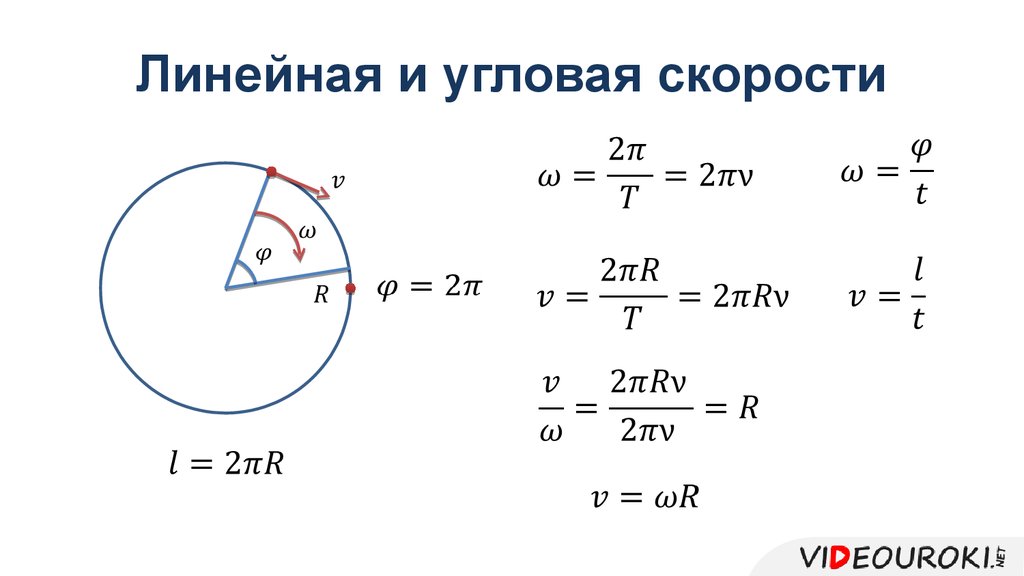
При движении по окружности: ω=vR(9). Или используя формулу (8) угловую скорость выразим как: ω=vrsinα (10).
Чему равна угловая скорость?
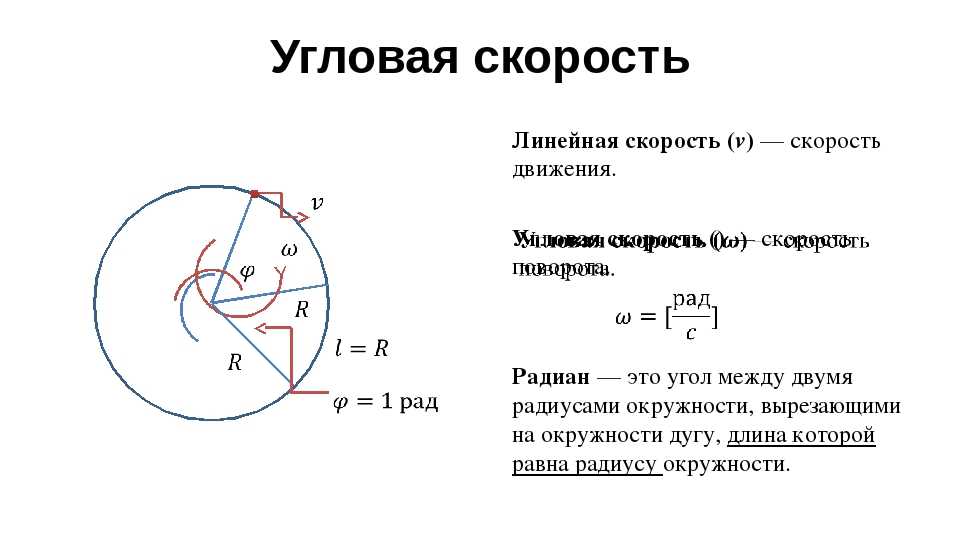
Угловая скорость численно равна углу поворота радиуса за единицу времени.
Как в физике обозначается угловая скорость?
Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени. Обозначение: ω (омега).
Как читается угловая скорость?
| Угловое ускорение | |
|---|---|
| СИ | рад/с2 |
| СГС | рад/с2 |
| Примечания | |
| псевдовектор | |
Как определить куда направлена угловая скорость?
Угловая скорость и угловое ускорение величины векторные. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис. 3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис. 3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
Куда направлено угловое ускорение при вращательном движении?
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора угловой скорости (рис. 1.
Как найти угловое перемещение?
Угловое перемещение равно произведению полного числа оборотов на 2π: 5.
Что такое угловой путь?
Таким образом, угловой путь можно вычислить за время как отношение изменения длины дуги к радиусу окружности, по которой движется точка твердого тела при вращении. … Число оборотов тела (точки) вокруг центра вращения за единицу времени называют частотой вращения.
В чем измеряется ускорение?
acceleratio ), характеризующая быстроту изменения скорости тела. Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2). Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с.
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2). Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с.
Что такое угловая скорость в каких единицах она измеряется?
Единицы измерения Единица измерения угловой скорости, принятая в Международной системе единиц (СИ) и в системах СГС и МКГСС, — радиан в секунду (русское обозначение: рад/с, международное: rad/s). В технике также используются обороты в секунду, намного реже — градусы, минуты, секунды дуги в секунду, грады в секунду.
Чему равна угловая скорость формула?
Уравнение равномерного вращения φ = φ0 + ωt; в случае начала отсчета от нулевого положения угол поворота φ = 0, тогда φ = ωt. Угловая скорость ω = ω0 + εt; при ω0 = 0 ω = εt.
Как найти радиус окружности по физике?
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Как посчитать количество оборотов в минуту?
Обороты в минуту конвертируются в обороты в секунду делением на 60: 1 об/мин = 1/мин = 1/(60 с) = 1/60 об/с ≈ 0,01667 об/с Обратное преобразование: обороты в секунду умножаются на 60 для перевода в обороты в минуту.
Чему равно центростремительное ускорение и как оно направлено?
Основные формулы центростремительного ускорения Центростремительное ускорение, которое также называют нормальным ускорением, всегда направлено к центру окружности, по которой движется точка. все время меняется, поэтому движение по окружности не является равноускоренным.
Что называют центростремительным ускорением?
Центростремительное (нормальное) ускорение — составляющая ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая составляющая, тангенциальное ускорение, характеризует изменение модуля скорости).
Куда направлено нормальное ускорение точки?
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело (см. рис. 4).
Какие силы создают центростремительное ускорение при движении шарика по окружности?
На шарик действуют две силы: сила тяжести и сила упругости нити. Они создают центростремительное ускорение, направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически.
Чему равно нормальное ускорение?
равно v2/r, где v — скорость точки, r — радиус кривизны траектории. При движении по окружности Н. у. может вычисляться по формуле rw2, где r — радиус окружности, w— угловая скорость вращения этого радиуса.
Чему равен модуль центростремительного ускорения?
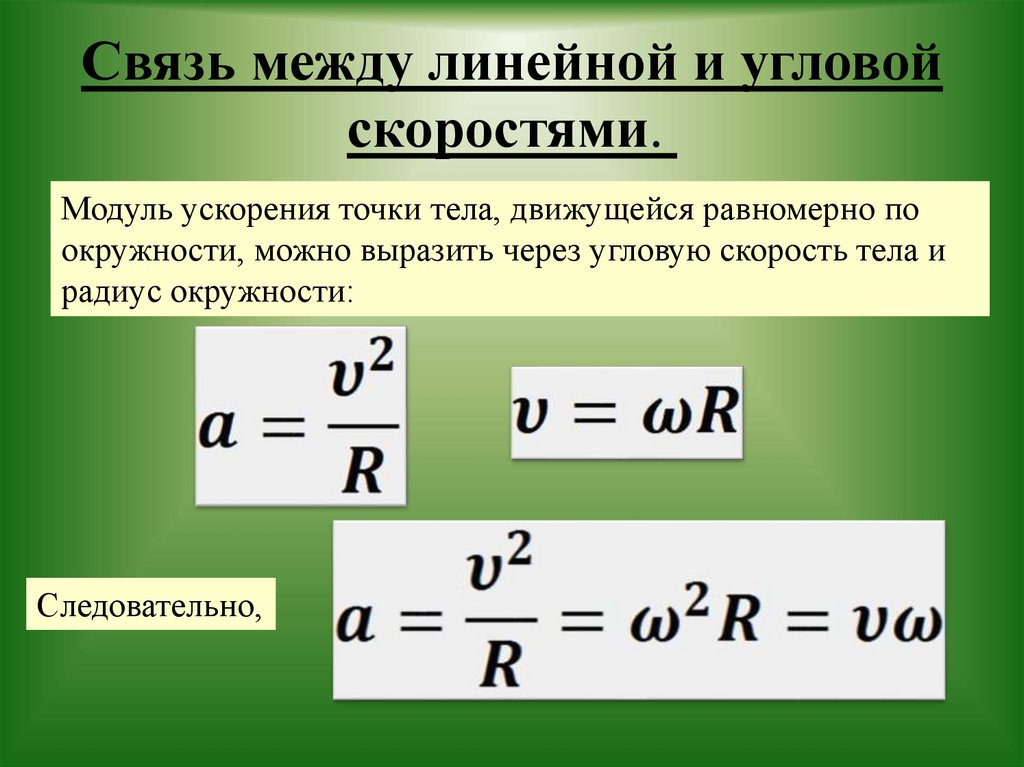
Модуль центростремительного ускорения равен: an=v2r=ω2r(1.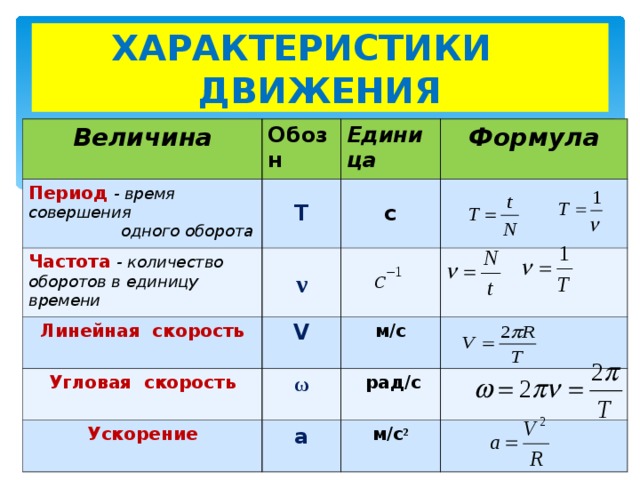
Как направлено центростремительное ускорение при движении тела по окружности?
При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.
Какой формулой ускорение тела равномерно движущегося по окружности?
Ускорение материальной точки при движении по окружности an=v2R=ω2R (6). При равномерном перемещении по окружности величина центростремительного ускорения постоянна (an=const). Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Куда направлена скорость тела при движении по окружности?
Скорость точки направлена по касательной к окружности в каждый момент времени. Ее называют линейной скоростью. При таком движении скорость точки меняется по направлению, а по модулю остается неизменной. Равномерное движение точки по окружности является движением с ускорением .
Ее называют линейной скоростью. При таком движении скорость точки меняется по направлению, а по модулю остается неизменной. Равномерное движение точки по окружности является движением с ускорением .
Какие силы действуют на тело при движении по окружности?
, сила реакции опоры (N), сила трения (Fтр) и сила тяги (F). При движении по дуге окружности возникает центростремительное ускорение, которое направлено к центру кривизны (перпендикулярно поверхно-сти).
Какая сила заставляет автомобиль двигаться?
При движении автомобиль преодолевает силы сопротивления качению, воздуха, подъема, инерции, а при движении на повороте на него действует боковая сила. Проявление сил, действующих на автомобиль при движении, может оказаться неожиданным для неопытного водителя и привести к дорожно-транспортному происшествию.
Какой смысл имеет центростремительное ускорение при движении тела?
Ответ: центростремительное ускорение всегда направлено к центру окружности.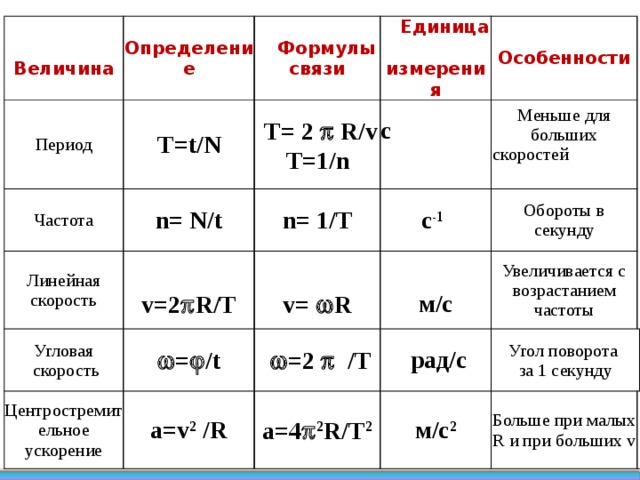 Смысл этой силы, например, натяжение нити при движении по окружности закреплённого на нити шарика или гравитационная сила притяжения со стороны звезды при вращении планеты вокруг звезды.
Смысл этой силы, например, натяжение нити при движении по окружности закреплённого на нити шарика или гравитационная сила притяжения со стороны звезды при вращении планеты вокруг звезды.
Куда направлена сила трения при движении по окружности?
Движение по окружности в горизонтальной плоскости радиус окружности, описываемой грузом. … При движении автомобиля сила трения направлена к центру окружности.
Угловое ускорение: среднее и мгновенное ускорение
Нам уже известно понятие ускорения тела. Так именуют величину, характеризующую изменение его скорости. Также нам известно понятие угловой скорости. Для характеристики этого изменения используют величину, называемую угловым ускорением. Рассмотрим его особенности и использование.
Определения углового ускорения тела. Среднее и мгновенное угловое ускорение
Определение 1
Угловым ускорением называется кинематическая величина, характеризующая изменение угловой скорости с течением времени.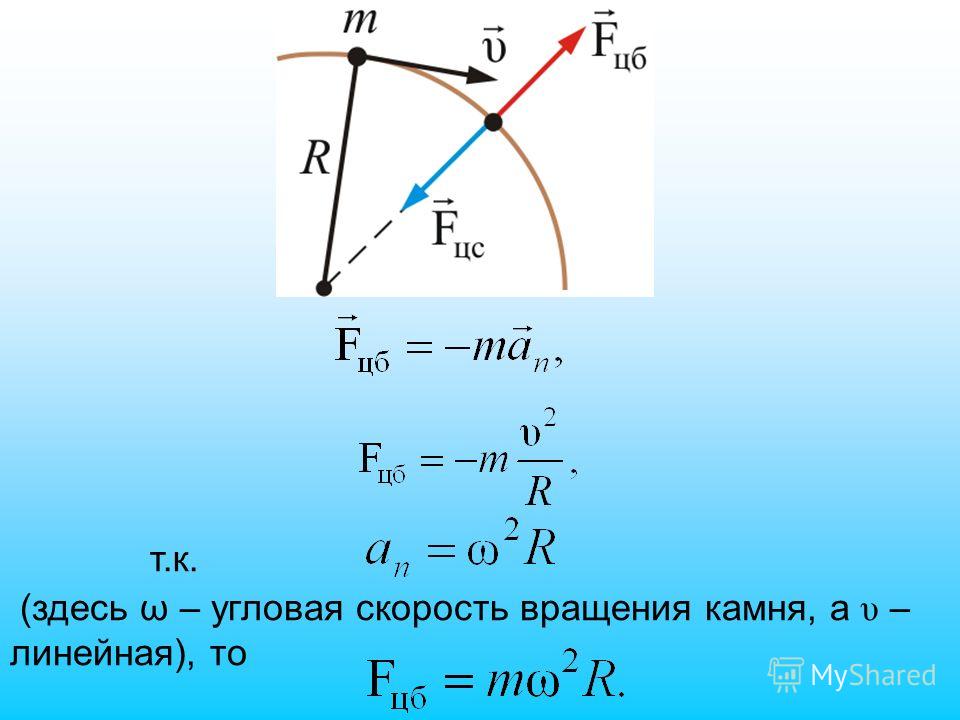 Обозначают его обычно греческой буквой ε.
Обозначают его обычно греческой буквой ε.
Слово «кинематическая» означает, что движение рассматривается без учёта действия на тело сил, независимо от них. Обозначим промежуток времени как Δt. Изменение угловой скорости за этот промежуток обозначим как Δω. Отношение Δω/Δt называют средним угловым ускорением. Среднее угловое ускорение равно угловой скорости за определённый интервал времени. Однако, как она себя вела, например, в самом его начале, середине или конце ничего не скажешь.
Если мы будем выбранный нами интервал времени постоянно уменьшать, изменение скорости получится описывать всё более и более точно. В идеале, чтобы Δt вообще стремился к нулю:
ε = lim (Δt→0)(Δω/Δt) = dω/dt = d2φ /d2t
Так мы перешли ко второму определению углового ускорения, только оно уже не среднее, а, как говорят, мгновенное.
Определение 2
Угловое ускорение тела есть первая производная его угловой скорости по времени или вторая производная его углового перемещения.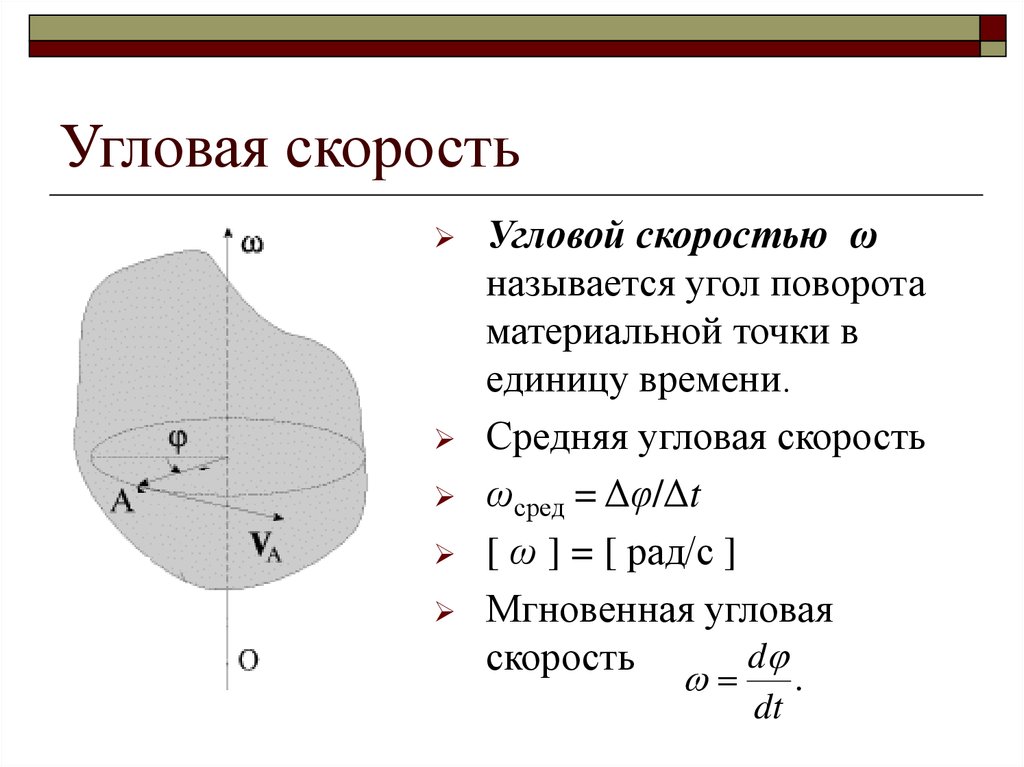 Ещё раз перепишем формулы, но уже в качестве официального определения.
Ещё раз перепишем формулы, но уже в качестве официального определения.
Угловое ускорение тела равно:
ε = dω/dt = d2φ /d2t
Размерностью величины будет 1/T2 (1/время2). Измеряют его обычно в радианах на секунду в квадрате, рад/с2 или 1/с2 (с-2).
Обязательно следует отметить, что ε может рассматриваться, в качестве вектора, т. е. ему приписывается направление. Хотя в отличие от направления обычной скорости, воспринимается это несколько сложнее, ведь наглядность отсутствует.
Угловое ускорение через радиус выражается как a = ε*R, где a – ускорение, направленное по касательной траектории.
Определения
Если тело вращается всё быстрее и быстрее, то это значит, что модуль его угловой скорости с течением времени увеличивается. Такое вращение называют ускоренным. При нём вектора угловых скорости и ускорения имеют одно и то же направление.
Если тело вращается всё медленнее и медленнее, то это значит, что модуль его угловой скорости со временем уменьшается. Такое вращение называют замедленным. При нём вектора угловой скорости и углового ускорения направлены противоположно.
Угловое ускорение и формула закона движения при равнопеременном вращении
Определение 5
Равнопеременным вращением называют вращение, при котором угловое ускорение не меняется с течением времени, т. е. является константой \[(ε=const)\].
Выведем его закон. Пусть в начальный момент времени (t=0) равен φ0, а его начальная скорость ω0.
Из определений выше следует
ε = dω/dt следует, что dω = ε dt.
Чтобы найти угловую скорость нам нужно найти первообразную от этого выражения по времени. Получаем
ω = εt + С1.
С1 – некоторая постоянная. В нашем случае, по начальным условиям, она равна начальной угловой скорости тела, ω0.
Поэтому
ω = εt + ω0
Напомним, что мгновенная угловая скорость равна: ω = dφ /dt
Отсюда
dφ /dt = εt + ω0
φ = (εt + ω0)dt
Находим первообразную по времени
φ = εt2/2 + ω0t + С2
С2 – некоторая постоянная. Исходя из начальных условий она равна φ0. Приходим к выражению
Исходя из начальных условий она равна φ0. Приходим к выражению
φ = εt2/2 + ω0t + φ0
Это и есть закон равнопеременного вращательного движения.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры
Пример. 1
Колесо стало вращаться с постоянным угловым ускорением и, спустя 10 оборотов от начала вращения, получило скорость 20 рад/с. Чему равно угловое ускорение?
Решение:
Применим к вращению колеса формулу равнопеременного движения, исходя из того, что его начальная угловая скорость ω0 была равна нулю. Формулы, с которыми нам придётся иметь дело:
φ = εt2/2; ω = εt; φ = 2πN
Из первой формулы выражаем ε
ε = (φ/t2)
Из второй формулы выражаем время
t = ω/ε
Подставляем его в формулу выше. {2}}\]
{2}}\]
После численных подстановок выясняем, что a точки равно 1,65 м/с2.
Ответ: Угловое ускорение точки равно (-4) рад/с2, а полное её ускорение – 1,65 м/с2.
Угловая скорость – определение, формула, рассмотрение жесткого тела и согласованность
Скорость – это термин, который используется в различных контекстах в нашей повседневной жизни. Например, как быстро мы ведем машину или как быстро мы бросаем мяч. Подобно этому контексту, скорость в основном определяется, или мы можем сказать, что это относится к тому, насколько быстро или медленно движется объект. поэтому угловую скорость можно определить как скорость вращения объекта. Если мы понимаем, то другими словами это описывается как изменение в единицу времени угла объекта.
поэтому, если мы собираемся рассчитать скорость вращательного движения, нам потребуется его угловая скорость. Формула угловых скоростей специально для расчета расстояния, которое проходит тело с точки зрения вращения и оборотов к затраченному времени.
Здесь упоминается довольно важная вещь — радианы. Всякий раз, когда мы можем рассчитать угловую скорость по углу, мы измеряем его в радианах. Радианы определяются как способ измерения углов, где мы определяем прямой угол — пи/2 радиан. Таким образом, один полный оборот содержит около 6,28 радиана.
Скорость — это фактор, с помощью которого мы можем определить, насколько медленно или быстро движется объект. Угловая скорость определяется как скорость объекта во вращательном движении.
Формула угловой скорости вычисляет расстояние, пройденное телом, в пересчете на количество оборотов или вращений за затраченное время. Она представлена символом ω и задается следующим образом:
Угловая скорость задается как = общее пройденное расстояние или общее затраченное время.
Пройденное расстояние, представленное символом θ и измеренное в радианах. Затраченное время измеряется в секундах. Таким образом, угловая скорость может быть выражена в радианах, то есть в секундах или в рад/с.
Угловая скорость, соответствующая одному полному обороту, обозначается как:
ω = 2π/t
Угловая скорость определяется как мера того, насколько быстро изменяется угол центра вращающегося тела во времени. В этой статье мы узнаем больше о формуле угловой скорости и взаимосвязи между угловой скоростью и линейной скоростью, а также о некоторых проблемах угловой скорости.
Скорость Земли
Угловая скорость может быть определена как скорость изменения углового смещения и определяется выражением:
ω=θt
где
θ определяется как угловое смещение
t определяется как время
ω Обозначается как угловая скорость
Угловая скорость устройства выражается в радианах в секунду. И угловая скорость, и угловая скорость представлены одной и той же формулой. Но следует очень тонко отметить, что угловая скорость сильно отличается от угловой скорости. Угловая скорость определяется как векторная величина, которая выражает как величину, так и направление, тогда как угловая скорость выражается только величиной.
Угловая скорость определяется как векторная величина, которая выражает как величину, так и направление, тогда как угловая скорость выражается только величиной.
Угловая скорость как векторное поле
Также можно показать, что спин векторного поля угловой скорости составляет ровно половину ротора векторного поля линейной скорости, которое обозначается как v(r) твердого тела. В символах это задается как:
ω = ½ ▽*v
Рассмотрение жесткого тела
[Изображение будет загружено в ближайшее время]
Положение точки P, расположенной в твердом теле, показанном синим цветом. Ri — это положение по отношению к раме лаборатории с центром в точках O и ri, а также положение по отношению к каркасу твердого тела с центром в точке O′. Исходная точка твердого тела находится в положении вектора R от рамки лаборатории.
Здесь не предполагается, что твердое тело всегда вращается вокруг своего начала. Его можно вращать вокруг произвольной точки, которая движется с линейной скоростью, обозначаемой как V(t) в каждый момент времени.
Его можно вращать вокруг произвольной точки, которая движется с линейной скоростью, обозначаемой как V(t) в каждый момент времени.
Для получения уравнений очень удобно представить твердое тело, прикрепленное к рамам, а затем рассмотреть систему координат, неподвижную относительно твердого тела. Затем мы рассмотрим преобразования координат, которые находятся между этой координатой и фиксированной «лабораторной» системой.
Как показано на рисунке выше справа, начало координат лабораторной системы находится в точке O, начало твердого тела находится в точке O′, а вектор от O к O′ равен R. Частица (i), которая в твердом теле находится в точке P, а положение вектора этой частицы R находится в системе отсчета lab и в позиции ri в системе отсчета тела. Видно, что положение частицы можно записать следующим образом:
Ri=R+ri
Консистенция
Мы уже обсуждали твердое тело, вращающееся вокруг произвольной точки. Определенное ранее вращение угловой скорости не зависит от выбора начала координат, что означает, что вращение угловой скорости является неотъемлемым свойством вращения твердого тела.
Определенное ранее вращение угловой скорости не зависит от выбора начала координат, что означает, что вращение угловой скорости является неотъемлемым свойством вращения твердого тела.
5.3: Скорость, ускорение и сила
-
- Последнее обновление
- Сохранить как PDF
-
- Идентификатор страницы
- 14461
- Безграничный
- Безграничный
- Выражают взаимосвязь между углом поворота и расстоянием
- Выразите центростремительное ускорение через скорость вращения
- Выразите уравнения для центростремительной силы и ускорения
- Когда объект вращается вокруг оси, точки на краях объекта перемещаются по дуге.
- Угол, огибаемый этими дугами, называется углом вращения и обычно обозначается символом тета .

- Мера того, насколько быстро объект вращается относительно времени, называется угловой скоростью. Обычно он представлен греческим символом омега . Как и его аналог линейной скорости, это вектор.
- Чтобы объект мог двигаться по кругу, он должен постоянно менять направление.
- Поскольку скорость является вектором, изменение направления приводит к изменению скорости.
- Изменение скорости называется ускорением. Изменение скорости из-за кругового движения известно как центростремительное ускорение.
- Центростремительное ускорение можно рассчитать, разделив квадрат линейной скорости на радиус окружности, по которой движется объект.
- Когда объект находится в равномерном круговом движении, он постоянно меняет направление и, следовательно, ускоряется. Это угловое ускорение.
- Сила, действующая на объект при равномерном круговом движении (называемая центростремительной силой), действует на объект из центра окружности.

- радиан : Угол, образуемый в центре окружности дугой окружности той же длины, что и радиус окружности.
- ускорение : Величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
- круговое движение : Движение таким образом, что выбранный путь является круговым.
- скорость : Векторная величина, обозначающая скорость изменения положения во времени или скорость с компонентом направления.
- центростремительный : направленный или движущийся к центру.
- угловая скорость : Векторная величина, описывающая круговое движение объекта; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
- Курирование и пересмотр.
 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
- OpenStax College, Угол вращения и угловая скорость. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/ . Лицензия : CC BY: Attribution
- радиан. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/radians . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Колледж OpenStax, угол поворота и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
- Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Колледж OpenStax, Центростремительное ускорение. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42084/latest/ .
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution
- Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/circular-motion . Лицензия : CC BY-SA: Attribution-ShareAlike
- скорость. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/velocity . Лицензия : CC BY-SA: Attribution-ShareAlike
- ускорение. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/acceleration . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики.
 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
- Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Центростремительное ускорение. Расположен по адресу : http://www.
 youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.jpg . Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Центростремительная сила. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42086/latest/ . Лицензия : CC BY: Attribution
- центростремительный. Предоставлено : Викисловарь. Расположен по адресу : http://en.
 wiktionary.org/wiki/centripetal . Лицензия : CC BY-SA: Attribution-ShareAlike
wiktionary.org/wiki/centripetal . Лицензия : CC BY-SA: Attribution-ShareAlike - Безграничный. Предоставлено : Безграничное обучение. Расположен по адресу : www.boundless.com//physics/definition/angular-velocity . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Колледж OpenStax, угол поворота и угловая скорость. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution - Угловая скорость. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Angular_velocity . Лицензия : CC BY: Attribution
- Центростремительное ускорение. Расположен по адресу : http://www.youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Центростремительное ускорение. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42084/latest/Figure_07_02_01a.
 jpg . Лицензия : CC BY: Attribution
jpg . Лицензия : CC BY: Attribution - Колледж OpenStax, Центростремительная сила. 25 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42086/latest/Figure_07_03_01a.jpg . Лицензия : CC BY: Attribution
- Обзор центростремительной силы. Расположен по адресу : http://www.youtube.com/watch?v=ldQWTNDBSSE . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
Угол поворота и угловая скорость
Угол поворота является мерой того, насколько сильно вращается объект, а угловая скорость измеряет, насколько быстро он вращается.
цели обучения
Угол вращения и угловая скорость
Когда объект вращается вокруг оси, например, автомобильная шина или пластинка на проигрывателе, движение можно описать двумя способами. Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перемещаться по дуге, перемещаясь на вращающемся объекте. Точка пройдет расстояние \(\mathrm{ΔS}\), но часто удобнее говорить о степени вращения объекта. Величина вращения объекта называется углом поворота и может измеряться в градусах или радианах. Поскольку угол поворота связан с расстоянием \(\mathrm{ΔS}\) и с радиусом \(\mathrm{r}\) уравнением \(\mathrm{Δθ=\frac{ΔS}{R}} \), обычно удобнее использовать радианы.
Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перемещаться по дуге, перемещаясь на вращающемся объекте. Точка пройдет расстояние \(\mathrm{ΔS}\), но часто удобнее говорить о степени вращения объекта. Величина вращения объекта называется углом поворота и может измеряться в градусах или радианах. Поскольку угол поворота связан с расстоянием \(\mathrm{ΔS}\) и с радиусом \(\mathrm{r}\) уравнением \(\mathrm{Δθ=\frac{ΔS}{R}} \), обычно удобнее использовать радианы.
Угол θ и длина дуги s : Радиус окружности поворачивается на угол \(\mathrm{Δθ}\). Длина дуги \(\mathrm{Δs}\) описана на окружности.
Скорость, с которой вращается объект, определяется угловой скоростью, которая представляет собой скорость изменения угла поворота во времени. Хотя угол сам по себе не является векторной величиной, угловая скорость является вектором. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки.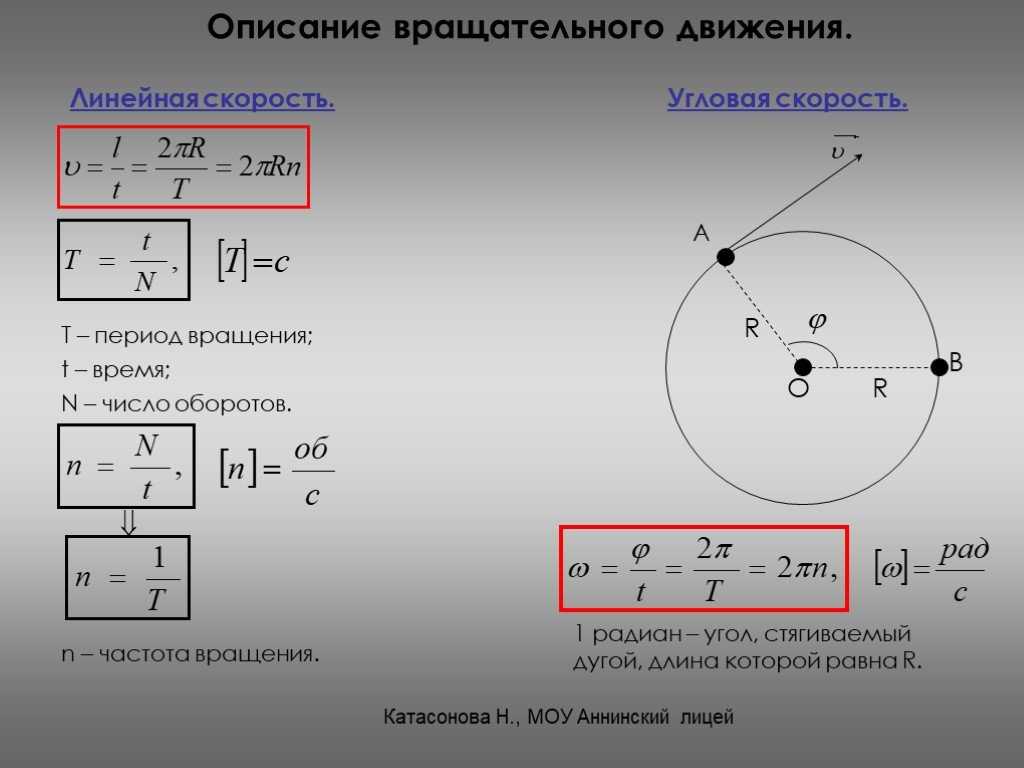 Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Направление угловой скорости : Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение. Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Когда ось вращения перпендикулярна вектору положения, угловую скорость можно рассчитать, взяв линейную скорость \(\mathrm{v}\) точки на краю вращающегося объекта и разделив ее на радиус. Это даст угловую скорость, обычно обозначаемую \(\mathrm{ω}\), в радианах в секунду.
Угловая скорость : Муха на краю вращающегося объекта регистрирует постоянную скорость \(\mathrm{v}\). Объект вращается с угловой скоростью, равной \(\mathrm{\frac{v}{r}}\).
Центростремительное ускорение
Центростремительное ускорение — это постоянное изменение скорости, необходимое объекту для сохранения кругового пути.
цели обучения
Обзор
Как упоминалось в предыдущих разделах о кинематике, любое изменение скорости определяется ускорением. Часто изменения скорости являются изменениями величины. Когда объект ускоряется или замедляется, это изменение скорости объекта. Изменения величины скорости соответствуют нашему интуитивному и повседневному использованию термина ускорение. Однако, поскольку скорость является вектором, она также имеет направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Равномерное круговое движение предполагает перемещение объекта по круговой траектории с постоянной скоростью. Поскольку скорость постоянна, обычно не думают, что объект ускоряется. Однако направление постоянно меняется по мере того, как объект пересекает круг. Таким образом, говорят, что он ускоряется. Это ускорение можно почувствовать, когда едешь на американских горках. Даже если скорость постоянна, быстрый поворот вызовет у гонщика ощущение силы. Это чувство — ускорение.
Даже если скорость постоянна, быстрый поворот вызовет у гонщика ощущение силы. Это чувство — ускорение.
92r}\]
, где омега — скорость вращения, определяемая выражением \(\mathrm{\frac{v}{r}}\).
Центростремительное ускорение : Когда объект движется по окружности, направление вектора скорости постоянно меняется.
Центростремительная сила
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой (примером центростремительной силы является равномерное круговое движение).
цели обучения
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой. Равномерное круговое движение является примером действия центростремительной силы. Это можно увидеть в движении спутников вокруг Земли, в натяжении веревки при игре в мяч, в петле на американских горках или в ведре, раскачиваемом вокруг тела.
Обзор центростремительной силы : Краткий обзор центростремительной силы.
Ранее мы узнали, что любое изменение скорости является ускорением. Когда объект движется по круговому пути, он постоянно меняет направление и, следовательно, ускоряется, в результате чего на объект действует постоянная сила. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому следует объект, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно вращаете его по кругу. 92}\]
Ключевые точки
Ключевые термины
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЕННОЕ РАНЕЕ
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
Эта страница под названием 5.3: Velocity, Acceleration, and Force распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.
 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
 org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution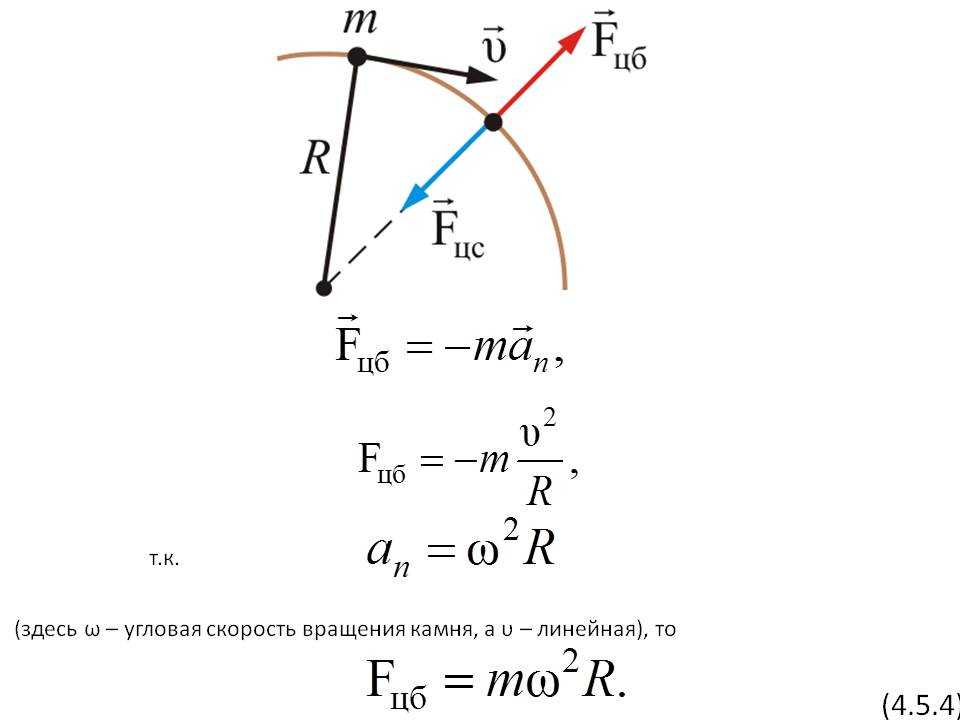 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution
 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42083/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
 youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube
youtube.com/watch?v=EX5DZ2MHlV4 . Лицензия : Общественное достояние: неизвестно Авторские права . Условия лицензии : Стандартная лицензия YouTube wiktionary.org/wiki/centripetal . Лицензия : CC BY-SA: Attribution-ShareAlike
wiktionary.org/wiki/centripetal . Лицензия : CC BY-SA: Attribution-ShareAlike org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution
org/content/m42083/latest/Figure_07_01_04a.jpg . Лицензия : CC BY: Attribution jpg . Лицензия : CC BY: Attribution
jpg . Лицензия : CC BY: Attribution