Задачи на движение по окружности с решением

Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только. 

Движение по окружности: определение, примеры

Движение по окружности – самый простой случай криволинейного движения. 

Примеры движения по окружности:

• грузовик движется по мосту с радиусом кривизны R;
• атлет крутит шар в руке, перед тем как бросить его;
• космическая станция летает по кругу над поверхностью Земли;
• катафот вращается на раскрученном колесе велосипеда.

Приведем ниже кинематические соотношения для поступательного и вращательного движений:

Вопросы на движение по окружности

Вопрос 1. Как направлено центростремительное ускорение?

Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.

Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?

Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.

Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?

Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.

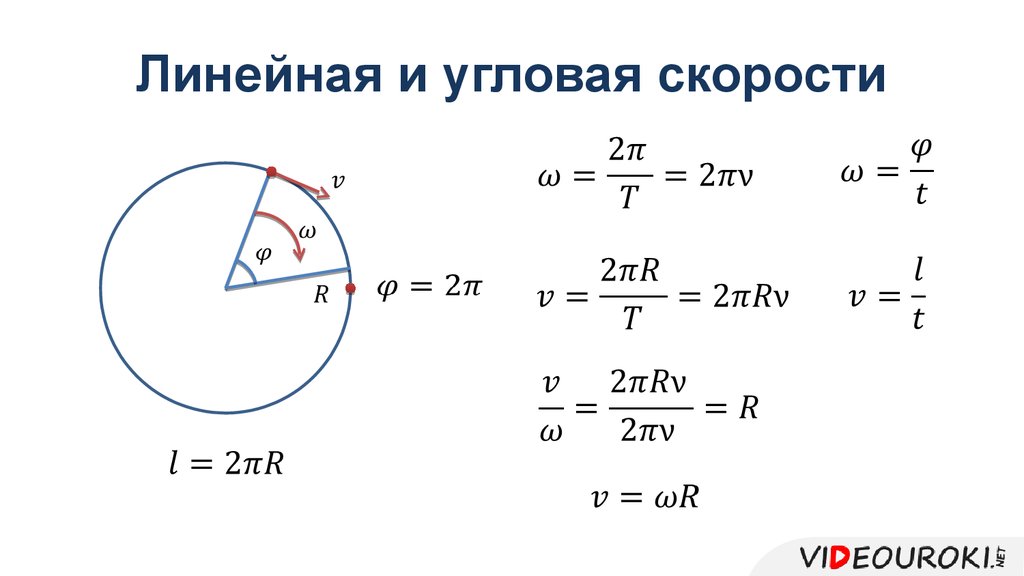
Вопрос 4. Что такое линейная и угловая скорость?

Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.

Вопрос 5.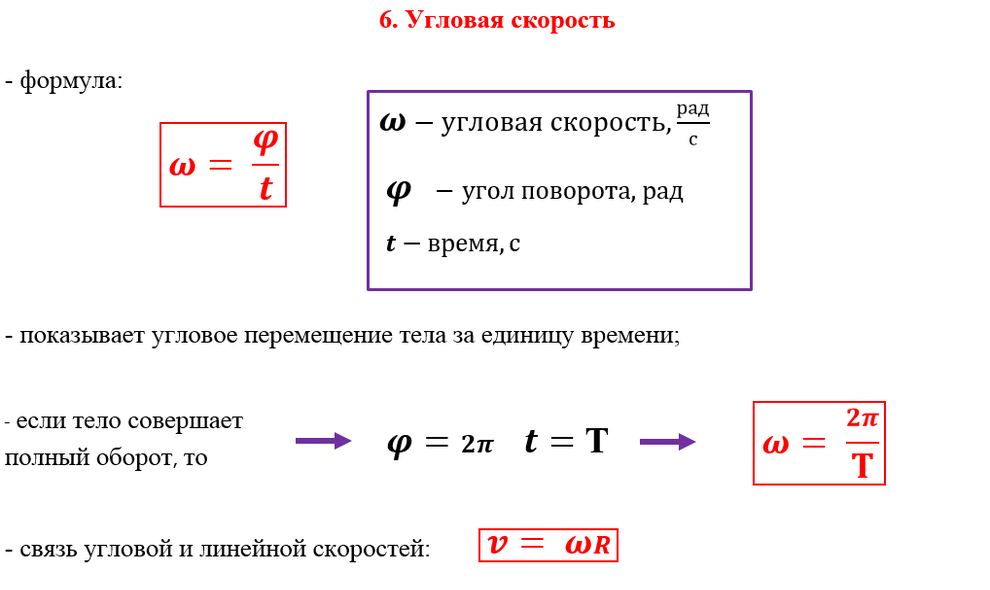 При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?

Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.

Задачи на движение по окружности

Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.

Задача №1. Нахождение линейной скорости при движении по окружности

Условие

Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?

Решение

В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:

Ответ: 10,9 м/с.

Задача №2. Нахождение углового ускорения

Условие

Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Решение

Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:

Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:

Ответ: 3,2 радиан на секунду в квадрате.

Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.

Задача №3. Нахождение скорости движения по окружности

Условие

Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?

Решение

Две точки вращаются на одном колесе, а значит, с одинаковой частотой. 2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.

Решение

Полное ускорение – векторная сумма нормального и тангенциального ускорений.

Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:

Подставляем значение t из условия и вычисляем:

 
Ответ: 1,65 метра в секунду.

Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.

Простая физика — EASY-PHYSIC

Задача 1. За промежуток времени с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость и модуль средней скорости .

Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению.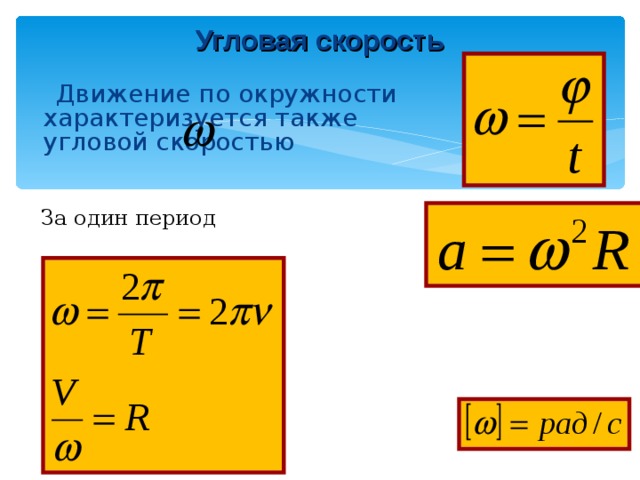 Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.

Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с

Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска . Найти геометрическое место всех точек диска,  скорость которых 2 м/с. Угол .

Скорость точек окружности

Решение:

Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра м/с.   Линейные скорости показаны для  точек оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга: .  В точке C скорости, напротив, сложатся, поскольку они сонаправлены: м/с.

Определим теперь скорости точек и . Понятно, что они будут равны численно, но направлены в разные стороны.

Осталось разобраться с точкой . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу . Углы, которые образуются между векторами, показаны на рисунке, в том числе угол . Тогда в параллелограмме угол , а так как

, то все углы в треугольнике равны и он равносторонний, то есть м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные , точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.

Пробуксовывание

Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса , если известно, что скорость нижней точки м/c, а верхней — м/c.

Решение:

Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше.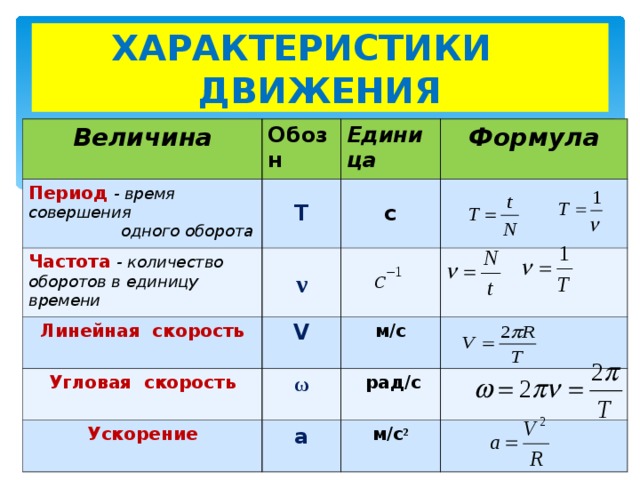 Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников и запишем отношения сходственных сторон:

Тогда

Тогда

Теперь обратимся к подобным треугольникам и . Для них отношение сходственных сторон равно:

Откуда м/с.

Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей и , при этом не забываем о векторном сложении скоростей, берем скорость со знаком «минус»:

м/с.

Ответ: 4 м/с.

Проскальзывание

Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А м/с, а нижней точки  B м/с. Определить скорость концов диаметра , перпендикулярного к , для того же момента времени. Под какими углами они направлены к горизонту?

Решение:

Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:

м/с.

Так как скорость точки есть результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра колеса , то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки , данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек и равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:

Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки можно найти как

Ответ: ,

Шарик катится по двум линейкам

Задача 5. Шарик радиусом см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно см, и за время с проходит см. С какими скоростями движутся верхняя и нижняя точки шарика?

На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка . Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника . Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки   будет

Таким же способом определяем скорость верхней точки :

Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.

Задача 6.  Автомобиль движется по закругленному шоссе, имеющему радиус кривизны м. Закон движения автомобиля имеет вид: , где м, м/с, м/с. Найти скорость автомобиля , его тангенциальное  , нормальное и полное ускорения в момент времени с.

Решение.

Путь:

Производная пути – линейная скорость:

Вторая производная – тангенциальное ускорение:

Нормальное ускорение:

Полное ускорение:

Задача7. Угол поворота диска радиусом см  изменяется со временем по закону . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.

Решение: угловая скорость – производная угла:

Угловое ускорение – производная угловой скорости:

Линейная скорость:

Задача 8.  Точка движется по окружности с постоянным угловым ускорением рад/. Найти угол между скоростью и ускорением  через 1 с после начала движения. Начальная скорость точки равна 0.

Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.

Известно, что нормальное ускорение  , тангенциальное ускорение . При этом , или . Тогда

Искомый угол:

Ответ:

Два концентрических колеса

Задача 9. Два концентрических колеса радиусами см и см вращаются с угловыми скоростями рад/c и рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси?  Проскальзывания нет.

Решение: определим радиус маленького (третьего) колеса, м:

Определим линейную скорость точек первого колеса:

Определим линейную скорость точек второго колеса:

Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:

Ответ: 20 рад/с

Задача 10. Гайку закручивают на болт за время . Длина болта , резьба составляет угол с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен .

Скорость вращения гайки по ходу завинчивания на болт

Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость (). Тогда .

Из рисунка видно, что

С другой стороны, так как длина болта , а гайка спускается по нему за время , то

Тогда

И можно определить :

Тогда

Ответ:

Как преобразовать об/мин в линейную скорость

Обновлено 14 февраля 2020 г.

Ли Джонсон

Вращательное движение — одна из самых важных вещей, которую нужно понимать при изучении классической физики, а преобразование скорости вращения в линейную — ключевая задача во многих задачах.

Само вычисление довольно простое, но оно усложняется, если угловая скорость (то есть изменение углового положения в единицу времени) выражается в нестандартной форме, такой как число оборотов в минуту (об/мин). Однако преобразовать число оборотов в минуту в скорость по-прежнему достаточно просто после того, как вы преобразуете число оборотов в минуту в более стандартную меру угловой скорости.

Об/мин Формула и пояснение

Об/мин – это число полных оборотов в минуту . Например, если колесо вращается так, что оно совершает один полный оборот в секунду, за 60 секунд оно совершит 60 оборотов и будет вращаться со скоростью 60 об/мин. Формула RPM, которую вы можете использовать для определения RPM в любой ситуации:

\text{RPM} = \frac{\text{Количество оборотов}}{\text{время в минутах}}

Из этой формулы вы можете рассчитать обороты в любой ситуации и даже если вы записываете количество оборотов меньше (или больше) минуты. Например, если колесо совершает 30 оборотов за 45 секунд (т. е. 0,75 минуты), результат будет следующим: 30 ÷ 0,75 = 40 об/мин.

Об/мин в угловую скорость

В большинстве случаев в физике используется угловая скорость ( ω ) вместо об/мин, которая по существу представляет собой угловое изменение положения объекта в секунду, измеряемое в радианах в секунду.

Это гораздо более удобный формат, когда вы конвертируете число оборотов в минуту в линейную скорость, потому что существует простое соотношение между угловой скоростью и линейной скоростью, которое не существует в явной форме для числа оборотов в минуту. Учитывая, что в полном обороте 2π радиан, RPM на самом деле говорит вам «количество 2π радиан оборотов в минуту».

Используя это, легко увидеть, как преобразовать число оборотов в минуту в угловую скорость: сначала преобразуйте значение в минуту в число в секунду, а затем преобразуйте число оборотов в значение в радианах. Вам нужна следующая формула:

ω = \frac{\text{об/мин}}{60 \text{секунда/минута}} × 2π \text{рад/об}

Проще говоря, вы делите на 60, чтобы преобразовать в оборотов в секунду, затем вы умножаете на 2π, чтобы превратить это в значение в радианах в секунду, то есть угловую скорость , которую вы ищете. Например, когда колесо в предыдущем разделе двигалось со скоростью 40 об/мин, вы конвертируете угловую скорость следующим образом:

\begin{align} ω &= \frac{40 \text{ об/мин}}{60 \text{ секунда/минута}} × 2π \text{ рад/об} \\ &= 4,19 \text{ рад/с } \end{aligned}

Угловая скорость в скорость

С этого момента преобразование из RPM в линейную скорость выполняется просто.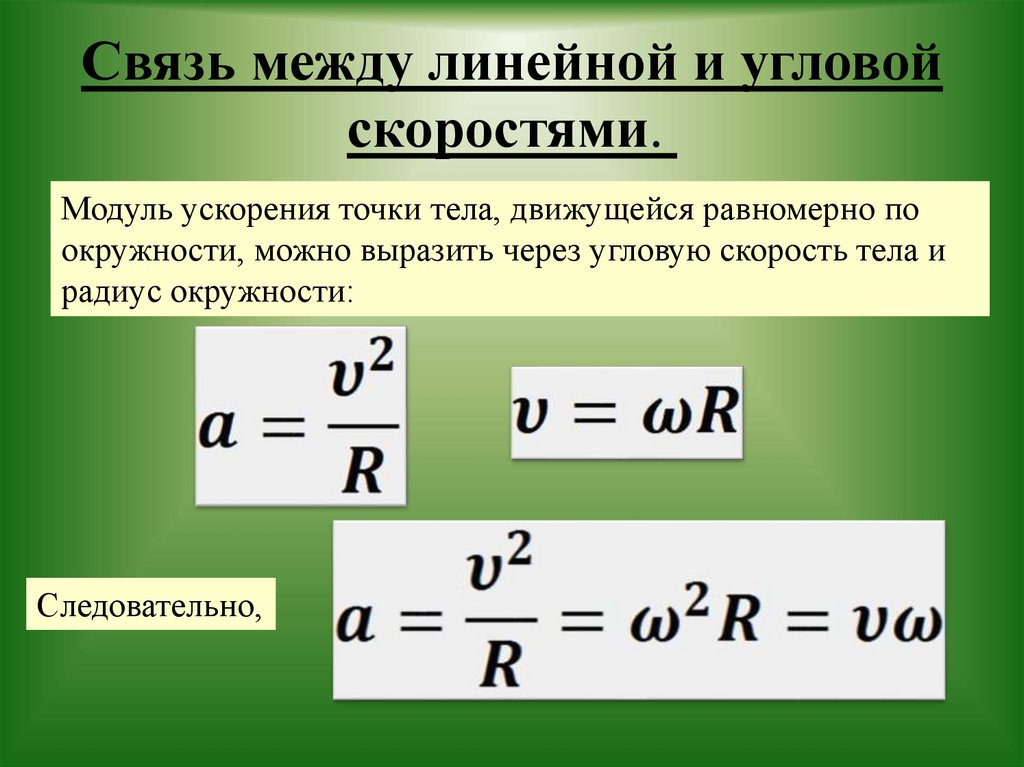 Нужна следующая формула:

v = ωr

Где ω — это угловая скорость, которую вы рассчитали на предыдущем шаге, а r — это радиус кругового пути для движения, и вы перемножаете их вместе, чтобы найти линейная скорость. Например, при вращении колеса со скоростью 40 об/мин, т.е. 4,19рад/с, при радиусе 15 см = 0,15 м скорость равна:

\begin{aligned} v &= 4,19 \text{ рад/с} × 0,15 \text{ м} \\ &= 0,63 \text { м/с} \end{aligned}

Есть несколько дополнительных моментов, о которых стоит помнить при выполнении этих вычислений. Во-первых, направление линейной скорости, которое вы рассчитываете, всегда по касательной к точке на окружности, для которой вы рассчитываете.

Например, если вы раскачиваете йо-йо по гигантскому кругу, но веревка порвется, йо-йо полетит в любом направлении, в котором оно двигалось на мгновенно оборвалась струна. Во-вторых, очень важно думать о единицах измерения при расчете оборотов в минуту. Единицы расстояния, которые вы используете для радиуса, будут такими же, как единицы расстояния в вашей конечной скорости, поэтому лучше придерживаться метров или футов, даже если число для радиуса окажется очень маленьким.

классическая механика. Преобразование угловой скорости в линейную посредством трения

спросил
10 лет, 11 месяцев назад

Изменено
5 лет, 8 месяцев назад

Просмотрено
2к раз

$\begingroup$

Очень простой вопрос здесь; это связано с этим, но не совсем то же самое.

Если вращающееся твердое тело (сфера для обсуждения) с массой $m$, радиусом $r$ и тензором инерции $I$ имеет начальную линейную скорость $v_0=0$ и ненулевую начальную угловую скорость $ \omega_0$, каковы идеализированные конечные угловая и линейная скорости, если тело мгновенно оказывается на поверхности с бесконечным трением и массой, в предположении, что $\omega_0$ параллелен поверхности (и поверхность не поглощает никакой энергии , ничего не теряется при нагревании)?

Тело должно катиться по поверхности с некоторой постоянной скоростью.