Коэффициент полезного действия – формула

4.7

Средняя оценка: 4.7

Всего получено оценок: 258.

4.7

Средняя оценка: 4.7

Всего получено оценок: 258.

В реальной жизни ни одно устройство не может работать без потерь энергии. Их минимизируют различными способами – уменьшением трения, уменьшением тепловых потерь и т.д. Показатель, который характеризует эффективность устройства, называется коэффициентом полезного действия.

Полезное действие

Рассмотрим устройство, которое поднимает груз массы m на высоту H. В идеальном случае работа совершается только против силы тяжести. Таким образом, энергия, которую необходимо затратить для подъема груза, равна mgH. Но в реальности в любом устройстве наличествует сила трения; а также сила тяжести действует и на само устройство.

Рис. 1. Подъем груза через блок.

Таким образом, та энергия, которую необходимо затратить в идеальном случае, называется полезной работой, а вся энергия, необходимая для выполнения задачи – затраченной работой.

Что такое коэффициент полезного действия

Отношение полезной работы к затраченной – это коэффициент полезного действия. Для двигателя внутреннего сгорания, на котором работает большая часть автомобилей, КПД колеблется в пределах 20-25%. Часть энергии тратится на нагрев деталей, часть – на преодоление трения, вдобавок к этому не всё топливо сгорает, а еще большая доля тепла выходит с выхлопными газами. Для сравнения КПД электромобиля составляет примерно 94%.

Рис. 2. Потери ДВС.

Формула коэффициента полезного действия в общем виде выглядит так:

$\eta = {A \over Q}$,

где А – полезная работа, а Q – вся энергия, затраченная на выполнения задачи

КПД теплового двигателя циклической машины определяется по формуле:

$\eta = {Q_1 – Q_2 \over Q_1}$,

где $Q_1 – Q_2$ – разность полученного тепла и тепла, отданного холодильнику.

Максимальный КПД теплового двигателя, работающего по циклу Карно, равен:

$\eta = {T_1 – T_2 \over T_1}$,

где $T_1$ – температура нагревателя, а $T_2$ – холодильника.

Рис. 3. Цикл Карно.

В случае электродвигателя КПД можно найти по формуле:

$\eta = {P_2 \over P_1}$,

где P_2 – полезная мощность, затраченная на преобразование электрической энергии в механическую, а P_1 – общая мощность двигателя.

Задачи

• В чайник налили 1,5 л холодной воды, ее температура – 283˚ К. Чтобы довести ее до кипения, понадобилось 6 минут. Сила тока, потребляемая чайником – 11 А. Напряжение в электрической сети – 228 В. Рассчитать КПД чайника.

Решение

Полезной работой в этом случае будет энергия, которая необходима для разогрева воды от 283˚ К до 373˚ К. Затраченной работой будет мощность чайника, умноженная на время закипания. Поэтому формулу КПД чайника запишем так:

$\eta = {cm(T_2 – T_1) \over Pt}$

Так как $m = \rho V$, а $P = UI$, то окончательная формула КПД чайника будет выглядеть так:

$\eta = {c\rho V (T_2 – T_1) \over UIt}$

Подставив в нее данные из условия, получим, что $\eta = 0,63$. Или в процентах – 63%.

• С помощью механического устройства груз массой 9 кг подняли на 20 м. КПД устройства – 70%. Найти силу, которую необходимо приложить к устройству, чтобы поднять груз.

Решение

$\eta = {mgH \over A}$, но так как $A = {F \cdot H}$, то $F = {mg \over \eta}$

И $F = {90 \over 0,7} = 130 Н$ – сила, которую необходимо приложить к устройству.

Что мы узнали?

В ходе урока были разобраны два важнейших понятия – полезная работа и затраченная работа, было дано определение коэффициента полезного действия, приведена его общая формула, а также ее частные вариации для различных устройств. В заключении урока разобраны две задачи.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Вася Васильев

  5/5

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 258.

А какая ваша оценка?

Коэффициент полезного действия | Физика

Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу A_з и полезную работу A_п. Если, например, наша цель — поднять груз массой m на высоту h, то полезная работа — это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:

    A_п = F_тh = mgh.      (24.1)

Если же мы применяем для подъема груза блок или какой-либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:

A_з > A_п

Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.

Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.

Сокращенное обозначение коэффициента полезного действия — КПД.

Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.

Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой η (читается «эта»):

    η =* 100%    (24.2)

Поскольку числитель A_п в этой формуле всегда меньше знаменателя A_з, то КПД всегда оказывается меньше 1 (или 100%).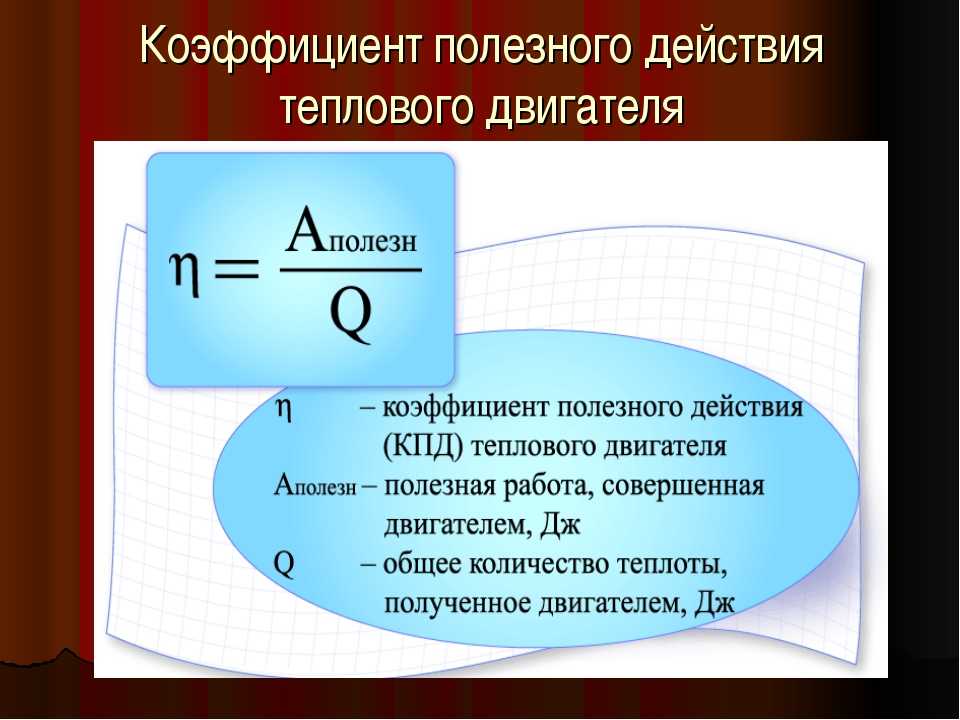

Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:

    A_з ≈ A_п     (24.3)

Следует помнить, что выигрыша в работе с помощью простого механизма получить нельзя.

Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:

    F₁s₁ ≈ F₂s₂     (24.4)

Отсюда следует, что,

выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.

Этот закон называют «золотым правилом» механики. Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.

«Золотое правило» механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.

Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.

1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается «золотое правило» механики? Кто его автор? 6. Приведите примеры проявления «золотого правила» механики при использовании различных простых механизмов.

Калькулятор коэффициента эффективности Освальда | Рассчитать коэффициент эффективности Освальда

👎

Формула

Перезагрузить

👍

Освальд Фактор Эффективности Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовые единицы

Отношение длины крыла: 15 —> Преобразование не требуется

ШАГ 2: Вычисление формулы в единицу вывода

0,634903252151742 —> преобразование не требуется 9(0,68)))))-0,64

Что такое Удлинение крыла?

Удлинение крыла определяется как квадрат размаха, деленный на площадь крыла, и обозначается символом AR. Для прямоугольного крыла это уменьшает отношение размаха к длине хорды, как показано в правом верхнем углу рисунка.

Как рассчитать коэффициент эффективности Освальда?
9(0,68)))))-0,64

для расчета коэффициента эффективности Освальда. Коэффициент эффективности Освальда, аналогичный эффективности размаха, является поправочным коэффициентом, который представляет собой изменение лобового сопротивления при подъемной силе трехмерного крыла или самолета. Коэффициент полезного действия Освальда обозначается символом и .

Как рассчитать коэффициент эффективности Освальда с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для коэффициента эффективности Освальда, введите соотношение сторон крыла (AR) и нажмите кнопку расчета. Вот как можно объяснить расчет коэффициента эффективности Освальда с заданными входными значениями -> 9(0,68)))))-0,64
. Удлинение крыла определяется как отношение квадрата размаха крыла к площади крыла или размаху крыла к хорде крыла для прямоугольной формы в плане. (0,68))))))-0,64
. Чтобы рассчитать коэффициент эффективности Освальда, вам нужно Удлинение крыла (AR) . С помощью нашего инструмента вам нужно ввести соответствующее значение соотношения сторон крыла и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.

Доля

Скопировано!

Свободный ход: расчет коэффициента полезного действия в рублях

[Эта статья была впервые опубликована на Rstats — квантикс и любезно предоставлена ​​R-блогерами]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)

Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.

Ранее в этом году Джо Фрил опубликовал статью о факторе эффективности в беге. Коэффициент эффективности (EF) можно посмотреть в программе Training Peaks, и он описывает, как он рассчитывается. В этом посте описывается, как я вычислил EF в R, используя один файл gpx.

Что такое коэффициент эффективности (EF)?

По сути, EF — это среднее расстояние, на которое вы продвигаетесь вперед за один удар сердца. Чем выше число, тем эффективнее вы бежите.

Для расчета EF вам нужны данные о скорости и частоте сердечных сокращений. В сообщении Джо он приводит следующий пример (используя имперские единицы измерения):

Для бега с нормализованным темпом 7,5 мин/миля (8 миль в час) скорость в ярдах в минуту составляет 234,7 (1760 ярдов * 8). /60). Если средняя частота сердечных сокращений равна 150, EF составляет 1,56 (234,7/150).

Я не использовал тренировочные пики, но кажется, что EF дается как единая мера для всей вашей пробежки. Должна быть возможность рассчитать EF как скользящую меру, чтобы вы могли отслеживать любые изменения EF с течением времени или по конкретной местности во время бега. Так что это было моей другой мотивацией для расчета EF в R.

Получение данных в R

Я использую пакет trackeR для выполнения тяжелой работы по загрузке данных из файла gpx.

 библиотека (трекер)
библиотека (ggplot2)
библиотека (зоопарк)
библиотека (хмс)
библиотека (сеткаExtra)
# выбираем файл gpx
путь к файлу <- файл.выбрать()
runDF <- readGPX (файл = путь к файлу, часовой пояс = "GMT")
 

Это дает нам данные из файла gpx во фрейме данных с именем runDF. Теперь нам нужно рассчитать нормализованную градуированную скорость. Для этого сначала вычисляются расстояния между точками, высоты и, следовательно, градиенты между точками. Точка-точка здесь относится к частоте дискретизации GPS-устройства. Мы также можем извлечь эту информацию, чтобы рассчитать скорость.

Вот код, который возвращает нас к нормализованной градуированной скорости. Вычисление столбца dist_adj описано ниже.

 # рассчитать расстояние между точками из кумулятивного расстояния
runDF$dist_point <- c(0,diff(runDF$distance, lag=1))
# рассчитываем градиент от точки к точке как %
runDF$alti_point <- c(0,diff(runDF$altitude, lag=1))
runDF$grad_point <- (runDF$alti_point / runDF$dist_point) * 100
runDF$dist_adj <- runDF$dist_point *
  (0,98462 + (0,030266 * runDF$grad_point) +
     (0,0018814 * runDF$град_точка ^ 2) +
     (-3.  4))
# расчет времени
runDF$time_temp <- strptime(runDF$time, format = "%Y-%m-%d %H:%M:%S")
runDF$time_point <- c(0,diff(as.vector(runDF$time_temp), lag=1))
runDF$time_temp <- NULL
runDF$time_cumulative <- cumsum(runDF$time_point)
runDF$time_hms <- as_hms(runDF$time_cumulative)
# скорость в м/с
runDF$speed <- runDF$dist_point / runDF$time_point
# нормализованная ступенчатая скорость в м/с
runDF$ngs <- runDF$dist_adj / runDF$time_point
# заменить NaN на 0
runDF[is.na(runDF)] <- 0
# Коэффициент эффективности равен ngs в ярдах в минуту, деленным на частоту сердечных сокращений.
runDF$EF <- (1,0936133 * runDF$ngs * 60) / runDF$heart_rate
 

Как рассчитать нормализованный темп?

Если вы бежите в гору, ваш темп будет медленнее при беге по ровной поверхности (и наоборот). Можем ли мы нормализовать градиент, чтобы увидеть, насколько быстро бегун будет двигаться, если вся трасса будет плоской.

Существует статья 2002 г., в которой рассматриваются изменения темпа при различных уклонах (Minetti et al. (2002)). Однако это было небольшое исследование с участием 10 человек. В настоящее время у нас гораздо больше данных благодаря потребительским устройствам с поддержкой GPS. Strava использовала данные своих пользователей, чтобы создать новую модель для расчета GAP (темп с поправкой на оценку) для отображения на своем сайте. Их результаты сопоставлены с выводами Minetti et al. показаны здесь: 94))

Давайте посмотрим на наш графический вывод, прежде чем смотреть, как он был сгенерирован.

Пример выходных данных (EF показан синим цветом внизу справа)

Выходные данные показывают скорость, высоту над уровнем моря, нормализованную градуированную скорость, частоту сердечных сокращений и EF. Пример, показанный выше, имеет несколько интервалов (обратите внимание на пики на графике сердечного ритма). EF довольно постоянен, но немного меняется во время интервалов/циклов отдыха.

Оставшийся код

Приведенные выше графики были сгенерированы с использованием этого кода.

 # Отметки на графиках форматируются в чч:мм
format_hm <- function(sec) stringr::str_sub(format(sec), end = -4L)
# делаем графики
p1 <- ggplot(runDF, aes(time_hms, скорость)) +
  geom_line (aes (альфа = 0,2)) +
  илим(0,5) +
  geom_line(aes(y = rollmean(скорость, 120, na.pad = TRUE)), color = "#663399", размер = 1) +
  масштаб_x_время (метки = format_hm) +
  labs(x = "Время", y = "Скорость (м/с)") +
  тема (легенда.позиция = "нет")
р1
p2 <- ggplot(runDF, aes(time_hms, высота)) +
  geom_line (цвет = "# E69F00") +
  масштаб_x_время (метки = format_hm) +
  labs(x = "Время", y = "Высота") +
  тема (легенда.позиция = "нет")
р2
p3 <- ggplot(runDF, aes(time_hms, ngs)) +
  geom_line (aes (альфа = 0,2)) +
  илим(0,5) +
  geom_line(aes(y = rollmean(ngs, 120, na.pad = TRUE)), color = "#663399", size = 1) +
  масштаб_x_время (метки = format_hm) +
  labs(x = "Время", y = "Нормализованная скорость градиента (м/с)") +
  тема (легенда.позиция = "нет")
р3
p4 <- ggplot(runDF, aes(time_hms,heart_rate)) +
  geom_line(цвет = "#D55E00") +
  илим (0,200) +
  масштаб_x_время (метки = format_hm) +
  labs(x = "Время", y = "Частота сердечных сокращений (уд/мин)") +
  тема (легенда. позиция = "нет")
п4
p5 <- ggplot(runDF, aes(time_hms,EF)) +
  geom_line (aes (альфа = 0,2)) +
  илим(0,5) +
  geom_line(aes(y = rollmean(EF, 120, na.pad = TRUE)), color = "#0072B2", size = 1) +
  масштаб_x_время (метки = format_hm) +
  labs(x = "Время", y = "Коэффициент эффективности") +
  тема (легенда.позиция = "нет")
р5
# упорядочиваем участки в лоскутное одеяло и сохраняем
q1 <- grid.arrange(p1,p2,p3,p4,p5, layout_matrix = rbind(c(1,2,3),c(4,5,5)))
saveName <- paste("./Output/Plots/",sub(".gpx",".png",basename(filepath)),sep = "")
ggsave(имя_сохранения, q1)
 

Большинство частей этого кода являются стандартными для ggplot. Два исключения:

• Чтобы получить скользящее среднее, я использовал пакет zoo и рассчитал 2-минутное (120-секундное) окно с помощью rollmean
• Подавление секунд на оси X было выполнено с помощью format_hm. Это указано в коде и изменяет время чч:мм:сс на чч:мм

—

Название поста взято из «Running Free» Iron Maiden с их одноименного дебютного LP.