Линейная скорость и угловая скорость формула: Формула линейной скорости в физике

26 января, 2023
Разное
By alexxlab

Содержание

1.9.2 Угловая и линейная скорости вращения

Вращательное движение вокруг неподвижной оси — еще один частный случай движения твердого тела.

Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4).
В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов.
Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути. Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол — угол между осью ОХ и радиус-вектором , определяющим положение точки А (см. рис.2.5).
Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое — на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза.
Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению
Угловая скорость выражается в радианах в секунду (рад/с).
Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска — около 140 рад/с¹.
Угловую скорость можно выразить через частоту вращения, т. е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:
Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1)
Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2.1) равен:
Если , то , или .
Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается.
Тем самым мы можем описать положение точек вращающегося тела в любой момент времени.
Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.
Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.
Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:
Так как , то
Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли .
Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:
Следовательно,
Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет.
Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами , можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени. Знаем мы и направления и , a также форму траекторий точек.

формула, единица измерения, как рассчитать через обороты в минуту и радиус

Содержание:

Что такое линейная скорость, единицы измерения
- Связь между линейной и угловой скоростями

Формулы для нахождения линейной скорости

Модуль скорости

Задачи с примерами решения

Содержание

Что такое линейная скорость, единицы измерения
- Связь между линейной и угловой скоростями

Формулы для нахождения линейной скорости

Модуль скорости

Задачи с примерами решения

Что такое линейная скорость, единицы измерения

Определение

Скоростью при равномерном движении тела называют физическую величину, с помощью которой определяют путь, преодоленный телом за единицу времени.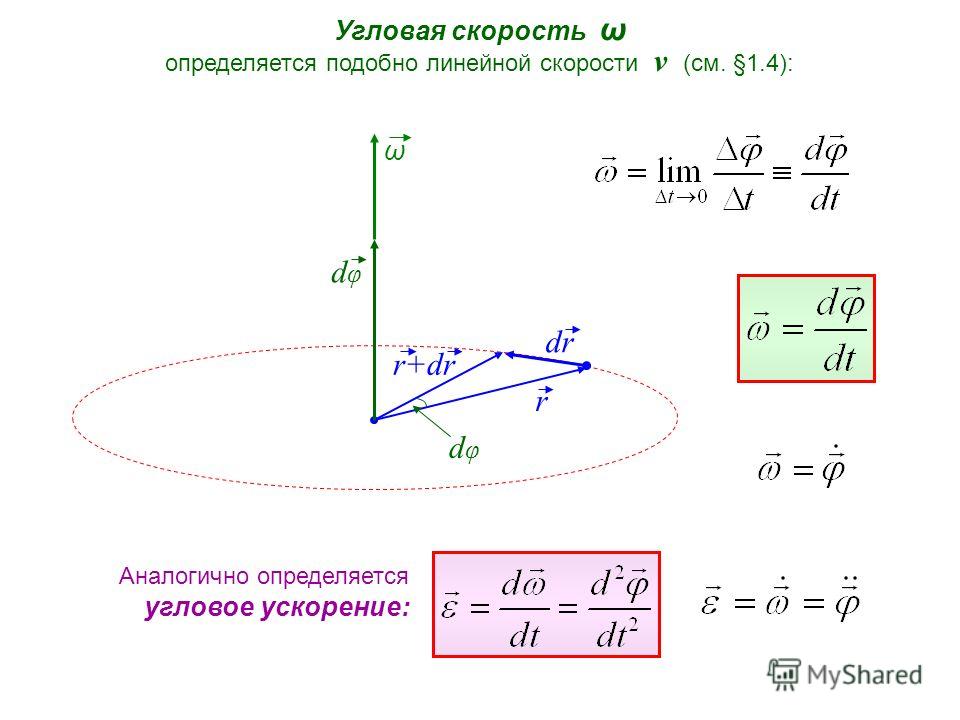

В международной системе СИ единицей измерения линейной скорости является производная от двух основных единиц:

метр;

секунда.

В международной системе СИ скорость измеряется в метрах в секунду (м/с). За единицу скорости принимают скорость равномерного движения, при которой путь в один метр тело преодолеет в течение одной секунды. Кроме того, скорость можно измерять в:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

км/ч;

км/с;

см/с.

Связь между линейной и угловой скоростями

Скорость точки, которая совершает круговое движение, называется линейной скоростью, чтобы отделить это понятие от термина угловая скорость. Во время вращения абсолютно твердое тело в разных точках будет обладать неодинаковыми линейными скоростями, но значение угловой скорости остается стабильным.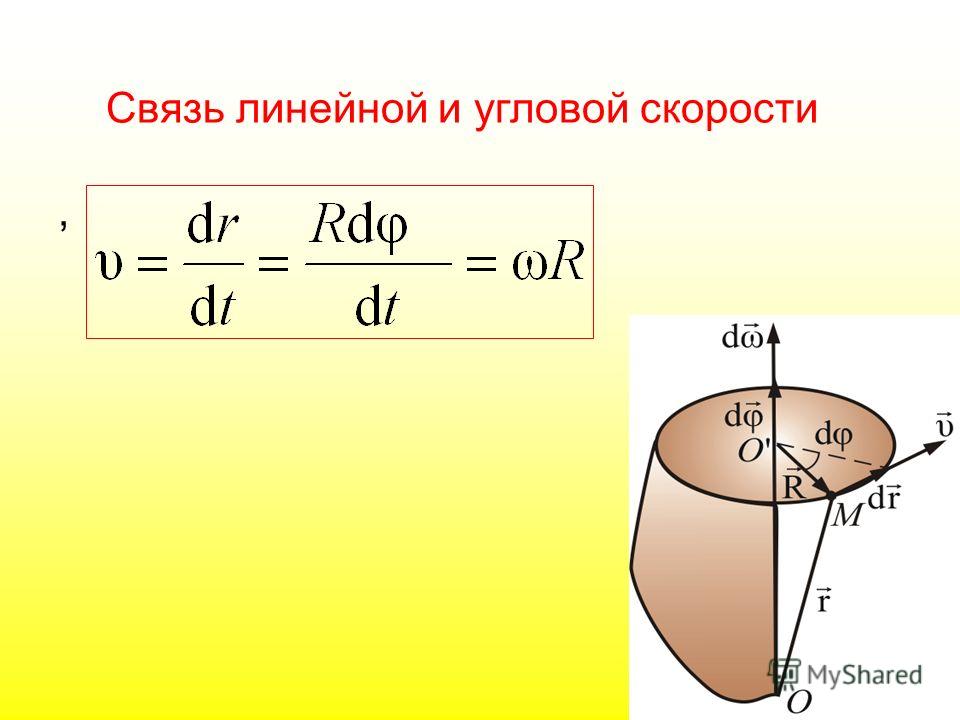

Источник: class-fizika.ru

Можно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет:

2πR

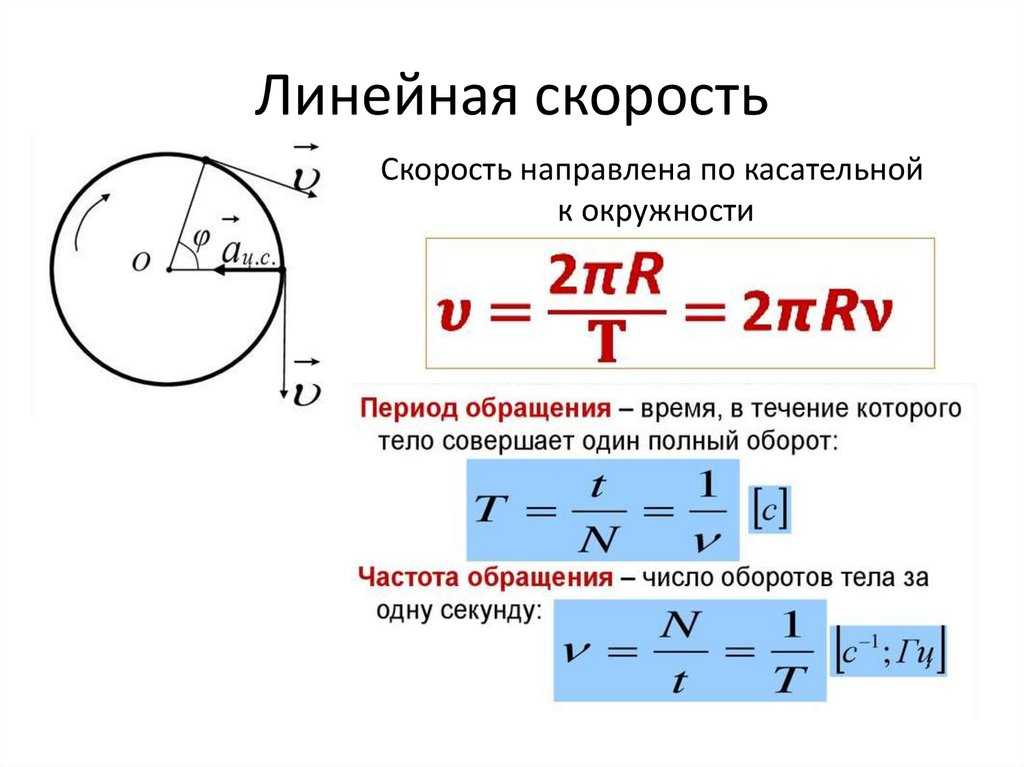
Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:

$v=\frac{2\pi R}{T}=2\pi RV$

Зная, что:

$\omega =2\pi V$

получим справедливое равенство:

$v=\omega R$

Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения. К примеру, точки, которые движутся по земному экватору v=463 м/с, а точки, расположенные на широте города Санкт-Петербург, движутся со скоростью v=233 м/с. При нахождении на полюсах планеты скорость уменьшается до v=0.

Модуль центростремительного ускорения точки тела, которая совершает равномерные вращательные движения, определяют с помощью угловой скорости тела и радиуса окружности. Уравнение будет записано в следующем виде:

$a=\frac{v^{2}}{R}$

$v=\omega R$

Таким образом, формула будет преобразована:

$a=\omega ^{2}R$

Подытожив расчеты, можно записать все возможные равенства, справедливые для определения центростремительного ускорения:

$a=\frac{v^{2}}{R}=\omega ^{2}R=\frac{4\pi ^{2}}{T^{2}}R=4\pi ^{2}V^{2}R$

Таким образом, рассматривают пару простейших движений, характерных для абсолютно твердого тела, включая поступательное и вращательное. При этом стоит отметить, что определить любое сложное движение, которое совершает абсолютно твердое тело, можно с помощью суммы двух независимых движений:

поступательное;

вращательное.

С помощью закона независимости движений описывают сложное движение абсолютно твердого тела.

Формулы для нахождения линейной скорости

Тело движется равномерно тогда, когда его скорость характеризуется постоянной величиной. Формула для расчета скорости такого движения будет иметь следующий вид:

V = st

где s является пройденным путем, то есть длиной линии;

t представляет собой время, в течение которого тело преодолевало указанный путь.

Определение

Линейной скоростью V называют физическую величину, которая демонстрирует путь, пройденный телом в течение определенного времени.

Основной формулой для определения линейной скорости является следующее равенство:

V = St

где S является путем,

t обозначает время, в течение которого тело преодолело путь S.

Иной вариант уравнения имеет такой вид:

V = lt

где l является путем,

t обозначает время, в течение которого тело преодолело дугу l.

В некоторых научных источниках скорость обозначают с помощью маленькой буквы v. Другим уравнением для расчета линейной скорости является равенство:

$v=2\pi RT$

В данном случае 2π представляет собой полную окружность и составляет 360 угловых градусов. Вектор скорости направлен по касательной к траектории движении тела.

Модуль скорости

Числовое значение скорости может быть разным в зависимости от выбранной единицы измерения. Кроме числового значения, скорость характеризуется направлением. Числовое значение, которым обладает скорость, в физике называют ее модулем.

В случае, когда скорость обладает определенным направлением, такая величина является векторной. Таким образом, скорость представляет собой векторную физическую величину. Записывают модуль скорости в виде буквы v, а вектор скорости, как $\vec{v}$

Следует отметить, что такие величины, как путь, время, длина обладают только числовым значением.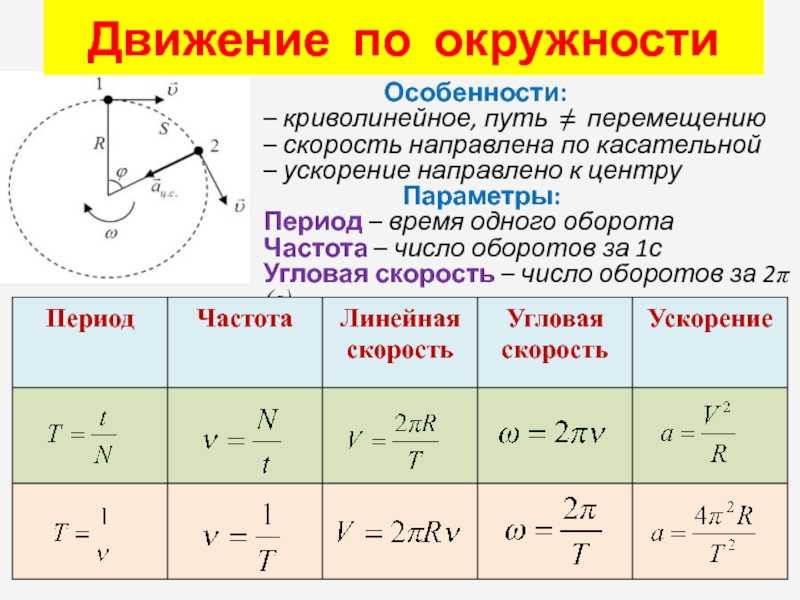 {2}}{R}\)

$v=\sqrt{aR}=\sqrt{40\times 3}=10.9$ м/с

Ответ: линейная скорость равна 10,9 м/с.

Задача №2

Поезд совершает равномерное движение. В течение 4 часов он преодолевает путь в 219 километров. Требуется рассчитать скорость движения поезда.

Решение:

Исходя из основной формулы для расчета линейной скорости, получим:

$v=\frac{S}{t}=\frac{219}{4}=54.75$ км/ч

Ответ: скорость движения поезда составит 54.75 км/ч или 15.2 м/с.

Задача №3

Транспортное средство, работая на двигателе внутреннего сгорания, в течение 2,5 часов преодолевает расстояние в 213 километров. Требуется определить скорость движения транспорта.

Решение:

С помощью уравнения расчета скорости можно записать решение задачи:

$v=\frac{S}{t}=\frac{213}{2,5}=85.2$ км/ч

Ответ: Скорость движение транспортного средства составляет 85.2 км/ч или 23.7 м/с.

Насколько полезной была для вас статья?

Рейтинг: 2. 80 (Голосов: 5)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Линейная и угловая скорость ‹ OpenCurriculum

Цели статьи

Для расчета скорости и угловой скорости объектов.

Понять взаимосвязь между линейной и угловой скоростью.

Радианная мера и длина дуги могут применяться для изучения кругового движения . В физике средняя скорость объекта определяется как:

$$\text{средняя скорость} = \frac{\text{пройденное расстояние}}{\text{истекшее время}}$$

Итак, предположим, что объект движется по окружности радиусом r, преодолев расстояние с за период времени t , как показано на рисунке 1. Тогда имеет смысл определить (среднюю) линейную скорость ν объекта как:

$$v = \frac{s}{t} \; \; \; \; (1)$$

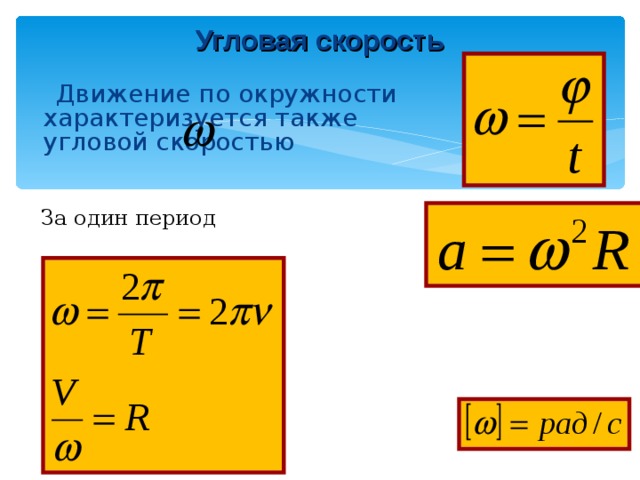
Пусть θ будет углом, сметаемым объектом за этот период времени.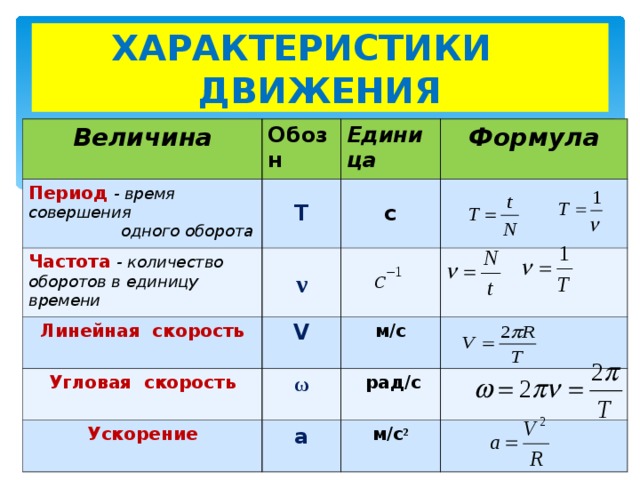 Затем мы определяем (среднюю) угловую скорость ω объекта как:

$$ω = \frac{θ}{t} \; \; \; \; (2)$$

Угловая скорость дает скорость, с которой центральный угол, огибаемый объектом, изменяется по мере того, как объект движется по окружности, и, таким образом, измеряется в радианах в единицу времени. Линейная скорость измеряется в единицах расстояния в единицу времени (например, в футах в секунду). Слово «линейный» используется потому, что выпрямление дуги, пройденной объектом по окружности, приводит к линии той же длины, так что можно использовать обычное определение скорости как расстояния во времени. Мы обычно опускаем слово «средняя» при обсуждении здесь линейной и угловой скорости.

Так как длина s дуги, отсеченной центральным углом θ в окружности радиусом r , равна s = r θ , то

$$v = \frac s}{t} = \frac{r θ}{t} = \frac{θ}{t} . r $$

так что мы получаем следующее соотношение между линейной и угловой скоростью:

$$v = ω r \; \; \; \; (3)$$

Пример 1

Объект заметает центральный угол $\frac{π}{3}$ радиан за 0,5 секунды, когда он движется по окружности радиусом 3 м. Найдите его линейную и угловую скорость за этот период времени.

Решение : Здесь мы имеем t = 0,5 сек, r = 3 м и θ = $\frac{π}{3}$ рад. Таким образом, угловая скорость ω равна

$$ ω = \ frac {θ} {t} = \ frac {\ frac {π} {3} рад} {0,5 сек} ⇒ ω = \ boxed {\ frac {2π {3} рад/сек}, $$

и, таким образом, линейная скорость ν равна

$$v = ω r = \left(\frac{2π}{3} рад/сек \right) (3 m) ⇒ \boxed{v = 2π м/сек}$$

Обратите внимание, что единицами измерения ω являются рад/сек, а единицами измерения ν – м/сек. Напомним, что радианы на самом деле безразмерны, поэтому в формуле ν = ωr исчезают единицы радианы.

Пример 2

Объект проходит расстояние 35 футов за 2,7 секунды, двигаясь по окружности радиусом 2 фута. Найдите его линейную и угловую скорость за этот период времени.

Решение : Здесь мы имеем t = 2,7 с, r = 2 фута и с = 35 футов.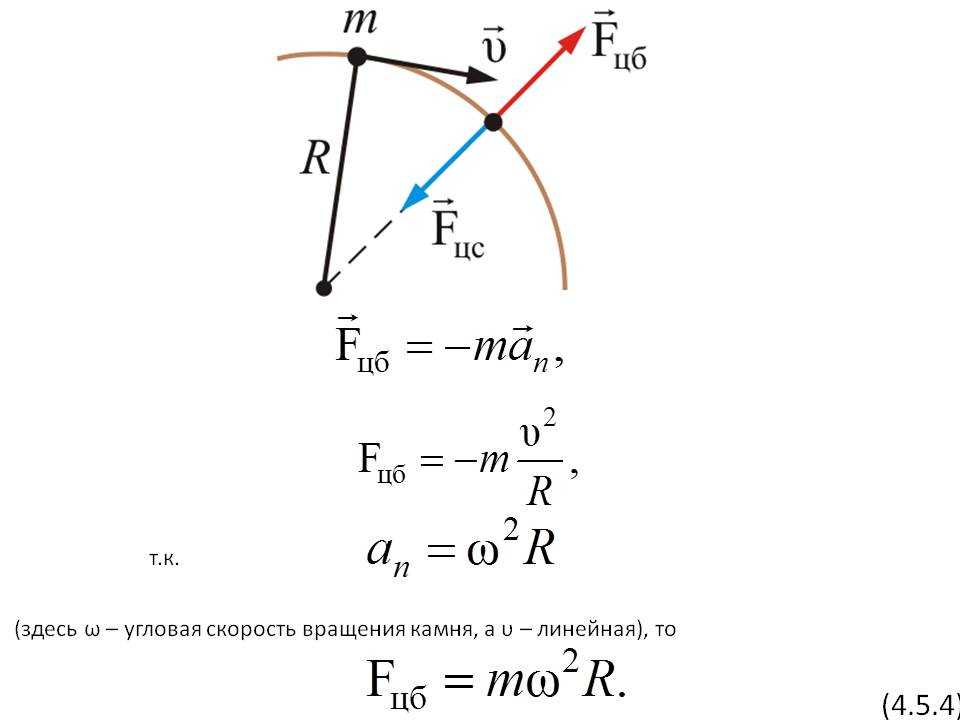 Таким образом, линейная скорость ν равно

$$v = \frac{s}{t} = \frac{35 футов}{2,7 с} ⇒ \boxed{12,96 фут/сек} , $$

и, следовательно, угловая скорость ω определяется как

$$v = ω r = 12,96 фут/сек = ω(2 фута) ⇒ \boxed{ω = 6,48 рад/сек}$$

Пример 3

Объект движется с постоянной линейная скорость 10 м/с по окружности радиусом 4 м. На какой центральный угол он уходит за 3,1 секунды?

Решение : Здесь у нас есть t = 3,1 с, ν = 10 м/с, r = 4 м. Таким образом, угол θ равен

$$s = rθ ⇒ θ = \frac{s}{r} = \frac{vt}{r} = \frac{(10 м/с)(3,1 с )}{4 м} = \в коробке{7,75 рад}. $$

Во многих физических приложениях угловая скорость выражается в оборотов в минуту , сокращенно об/мин . Чтобы преобразовать обороты в минуту, скажем, в радианы в секунду, заметьте, что, поскольку в одном обороте 2 π радиан, а в одной минуте 60 секунд, мы можем преобразовать N об/мин в радиан в секунду путем «отмены единиц» следующим образом:

$$N об/мин = N \frac{об}мин} . \frac{2π}{1 об.} . \frac{1 мин}{60 сек} = \frac{N . 2π}{60} рад/сек$$

Это работает, потому что мы всего лишь дважды умножили на 1. Преобразование в другие единицы измерения угловой скорости работает аналогичным образом. Переход в обратном направлении, скажем, от рад/сек к оборотам в минуту, дает:

$$N рад/сек = \frac{N . 60}{2π} об/мин$$

Пример 4

Шестерня с внешним радиусом r ₁ = 5 см движется по часовой стрелке, в результате чего блокирующая шестерня с внешним радиусом r ₂ = 4 см движется против часовой стрелки с угловой скоростью ω ₂ = 25 об/мин. Какова угловая скорость ω ₁ большей шестерни?

Решение : Представьте себе частицу на внешнем радиусе каждой шестерни. После того, как шестерни вращались в течение периода времени t > 0 круговое смещение каждой частицы будет одинаковым. Другими словами, S ₁ = S ₂, где S ₁ и S ₂ находятся на расстояниях, пройденные частицами на передачах с Radi R 9066666666666666666666666666666666666666666666666666666666666666 года. и r ₂ соответственно. Но с ₁ = ν ₁ т и с ₂ = ν ₂ t, где ν ₁ и ν ₂ — линейные скорости шестерен с радиусами r ₁ и r ₂ соответственно. Таким образом,

$$v_{1}t = v_{2}t ⇒ v_{1} = v_{2}$$

, поэтому по формуле (3) мы получаем фундаментальное соотношение между двумя шестернями:

$ $\boxed{ω_{1}r_{1} = ω_{2}r_{2}}$$

Обратите внимание, что это верно для любых двух передач. Таким образом, в нашем случае мы имеем

$$ω_{1}(5) = (25)(4) ⇒ \boxed{ω_{1} = 20 об/мин} .$$

4.4: Круговое движение — линейное и угловое Скорость

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 3327

Майкл Коррал
Schoolcraft College

Радианная мера и длина дуги могут быть применены к изучению круговое движение . В физике средняя скорость объекта определяется как:

\[ \text{средняя скорость} ~=~ \frac{\text{пройденное расстояние}}{\text{прошедшее время}}
\nonumber \]

Рис. 4.4.1

Итак, предположим, что объект движется по окружности радиусом $r$, преодолевая расстояние $s$ за период времени $t$, как на рис. 4.4.1. Тогда имеет смысл определить (среднюю) линейную скорость $\nu $ объекта как:

\[ \nu ~=~ \frac{s}{t}\label{eqn:linspeed} \]

Пусть $\theta $ будет углом, сметаемым объектом за этот период времени. Затем мы определяем (среднюю) угловую скорость $\omega $ объекта как:

\[ \omega ~=~ \frac{\theta}{t}\label{eqn:angspeed} \]

Угловая скорость дает скорость, с которой центральный угол, огибаемый объектом, изменяется по мере движения объекта по окружности, и, таким образом, измеряется в радианах в единицу времени. Линейная скорость измеряется в единицах расстояния в единицу времени (например, в футах в секунду). Слово «линейный» используется потому, что выпрямление дуги, пройденной объектом по окружности, приводит к линии той же длины, так что можно использовать обычное определение скорости как расстояния во времени. Мы обычно опускаем слово «средняя» при обсуждении здесь линейной и угловой скорости.

Так как длина $s$ дуги, отсекаемой центральным углом $\theta$ в окружности радиуса $r$, равна $s=r\,\theta $, мы видим, что

\[ \nu ~=~ \frac{s}{t} ~=~ \frac{r\,\theta}{t} ~=~ \frac{\theta}{t} \;\cdot\; г ~,
\номер \]

, так что мы получаем следующее соотношение между линейной и угловой скоростью:

\[ \nu ~=~ \omega\,r\label{eqn:linang} \]

Пример 4.14

Объект смещает центральный угол $\frac{\pi}{3} $ радиан за $0,5 $ секунд, когда он движется по окружности радиусом $3 $ м. Найдите его линейную и угловую скорость за этот период времени.

Решение:

Здесь мы имеем $t=0,5 $ сек, $r=3 $ м и $\theta = \frac{\pi}{3} $ рад. Таким образом, угловая скорость $\omega $ равна

\[ \omega ~=~ \frac{\theta}{t} ~=~ \frac{\dfrac{\pi}{3}~\text{rad} }{0.5~\text{sec}}
\quad\Rightarrow\quad \boxed{\omega ~=~ \frac{2\pi}{3}~\text{rad/sec}} ~,
\nonumber \ ]

и, следовательно, линейная скорость $\nu $ равна

\[ \nu ~=~ \omega\,r ~=~ \left( \frac{2\pi}{3}~\text{rad /сек} \справа) \,(3~\text{m})
\quad\Rightarrow\quad \boxed{\nu ~=~ 2\pi~\text{м/сек}} ~.
\nonumber \] Обратите внимание, что единицами измерения $\omega $ являются рад/сек, а единицами измерения $\nu $ являются м/сек. Напомним, что радианы на самом деле безразмерны, поэтому в уравнении $\nu=\omega\,r $ исчезают радианы.

Пример 4.15

Объект проходит расстояние $35 $ футов за $2,7 $ секунд, двигаясь по окружности радиусом $2 $ футов. Найдите его линейную и угловую скорость за этот период времени. .

Решение:

Здесь у нас есть $t=2,7 $ сек, $r=2 $ фут и $s=35 $ фут.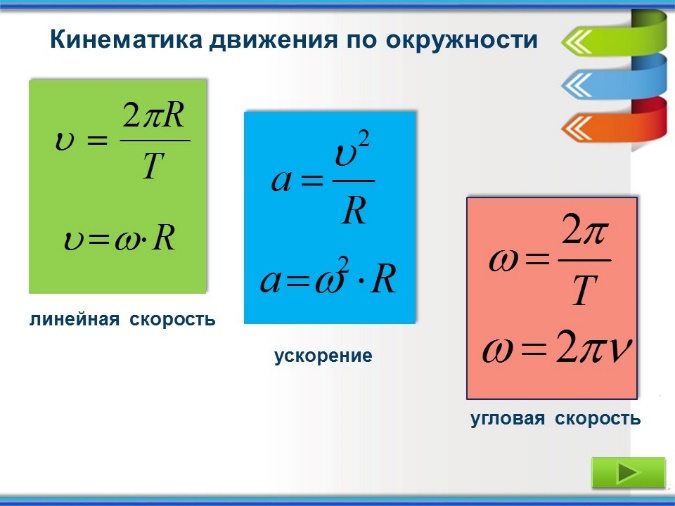 Таким образом, линейная скорость $\nu $ равна

\[ \nu ~=~ \frac{s}{t} ~=~ \frac{35~\text{feet}}{2.7~\text{sec}} \quad\Rightarrow\quad
\boxed{\ nu ~=~ 12.96~\text{ft/sec}} ~,
\nonumber \]

и, таким образом, угловая скорость $\omega $ определяется как

\[ \nonumber
\nu ~=~ \ omega\,r \quad\Rightarrow\quad 12.96~\text{ft/sec} ~=~ \omega\,(2~\text{ft})
\quad\Rightarrow\quad \boxed{\omega ~=~ 6,48~\текст{рад/сек}} ~.
\номер \]

Пример 4.16

Объект движется с постоянной линейной скоростью $10 $ м/сек по окружности радиусом $4 $ м. На какой центральный угол он уходит за $3,1$ секунды?

Решение:

Здесь мы имеем $t=3.1 $ сек, $\nu=10 $ м/сек и $r=4 $ м. Таким образом, угол $\theta $ равен

\[ s ~=~ r\,\theta \quad\Rightarrow\quad \theta ~=~ \frac{s}{r} ~=~ \frac {\nu\,t}{r} ~=~
\frac{(10~\text{м/сек})\,(3.1~\text{сек})}{4~\text{м}} ~ =~ \boxed{7.75~\text{rad}} ~.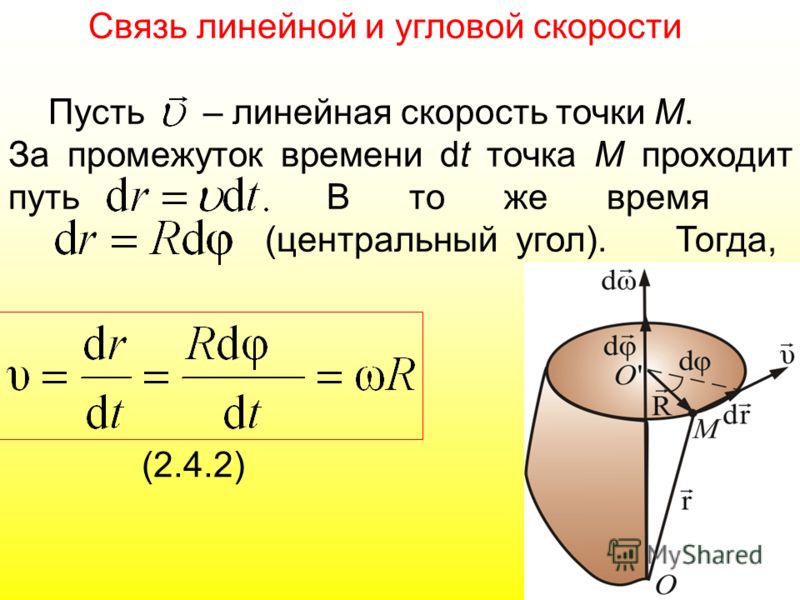
\номер \]

Во многих физических приложениях угловая скорость выражается в оборотов в минуту , сокращенно об/мин. Чтобы преобразовать обороты в минуту, скажем, в радианы в секунду, обратите внимание, что поскольку в одном обороте содержится $2\pi $ радиан, а в одной минуте $60 $ секунд, мы можем преобразовать $N $ об/мин в радиан в секунду путем «отмены единиц» следующим образом:

\[\require{cancel} \nonumber
N~\text{rpm} ~=~ N~\frac{\cancel{\text{rev}}}{\cancel{\text{min}}} \;\ cточка\;
\frac{2\pi~\text{rad}}{1~\cancel{\text{rev}}}
\;\cdot\; \frac{1~\cancel{\text{min}}}{60~\text{sec}} ~=~ \frac{N \cdot 2\pi}{60}~\text{rad/sec}
\ не число \]

Это работает, потому что все, что мы сделали, это дважды умножили на $1 $. Преобразование в другие единицы измерения угловой скорости работает аналогичным образом. Движение в обратном направлении, скажем, от рад/сек к оборотам в минуту, дает:

\[ N~\text{rad/sec} ~=~ \frac{N \cdot 60}{2\pi}~\text{rpm}
\nonumber \]

Пример 4.

Шестерня с внешним радиусом $r_1 = 5 $ см движется по часовой стрелке, заставляя блокируемую шестерню с внешним радиусом $r_2 = 4 $ см двигаться против часовой стрелки с угловой скоростью $\omega_2 = 25$ об/мин. Какова угловая скорость $\omega_1$ большей шестерни?

Рисунок 4.4.2

Решение:

Представьте себе частицу на внешнем радиусе каждой шестерни. После того, как шестерни вращаются в течение периода времени $t>0 $, круговое смещение каждой частицы будет одинаковым. Другими словами, $s_1 = s_2 $, где $s_1 $ и $s_2 $ — расстояния, пройденные частицами на шестернях с радиусами $r_1 $ и $r_2 $ соответственно.

Но $s_1 = \nu_1 \,t $ и $s_2 = \nu_2 \,t $, где $\nu_1 $ и $\nu_2 $ — линейные скорости зубчатых колес с радиусами $r_1 $ и $r_2 $ соответственно. Таким образом,

\[ \nu_1 \,t = \nu_2 \,t \quad\Rightarrow\quad \nu_1 = \nu_2 ~,
\nonumber \]

поэтому по уравнению \ref{eqn:linang} мы получаем фундаментальное соотношение между двумя шестернями:

\[
\boxed{\omega_1 \,r_1 ~=~ \omega_2 \,r_2}\label{eqn:gears}
\nonumber \]

Обратите внимание, что это верно для любых двух шестерни.

Blog Detail