Угловая скорость и угловое ускорение

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
2. если задан угол поворота φ за единицу времени:
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

• равномерное вращение (ω — const)
• равнопеременное вращение (ε — const)

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Сохранить или поделиться с друзьями

Вы находитесь тут:

Уважаемые студенты!

На нашем сайте можно получить помощь по техническим и другим предметам:

✔ Решение задач и контрольных

✔ Выполнение учебных работ

✔ Помощь на экзаменах

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Помощь с решением

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)

Поиск формул и решений задач

Формула угловой скорости в физике

Содержание:

• Определение и формула угловой скорости
• Равномерное вращение
• Формула, связывающая линейную и угловую скорости
• Единицы измерения угловой скорости
• Примеры решения задач

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность
с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота
$(\varphi)$ . Часто используют вектор элементарного поворота
$\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела
$(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой
$\omega$ . Математически определение угловой скорости записывают так:

$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$

Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее
с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости),
так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

$$\omega=\frac{\varphi}{t}(2)$$

где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот
($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:

$$\omega=\frac{2 \pi}{T}(3)$$

С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:

$$\omega=2 \pi \nu(4)$$

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения,
но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно
с данной мгновенной величиной скорости.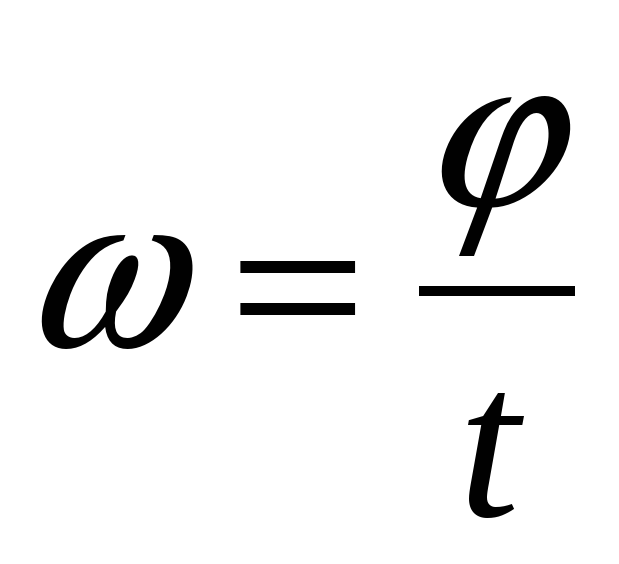 {3} \approx 20(\mathrm{rad})$$

Ответ. $\varphi = 20$ рад.

Читать дальше: Формула удельного веса.

направление вектора угловой скорости

направление вектора угловой скорости . Угловая скорость обычно измеряется в радианах в секунду, где радианы являются более естественным измерением угла, чем более привычные градусы. Но так же, как линейная скорость является вектором и, следовательно, имеет направление, угловая скорость тоже имеет направление. Итак, как направлен вектор угловой скорости?

Взаимосвязь между линейной скоростью и угловой скоростью

Как мы видели в блоге, где я ввел понятие угловой скорости, ее можно определить просто как угол, перемещаемый в единицу времени, или

, что, конечно же, приводит к тому, что она обычно измеряется в радианах в секунду. Однако мы также можем записать угловую скорость в терминах линейной скорости. Чтобы увидеть, как это сделать, давайте вспомним определение радиан , более естественную единицу измерения угла.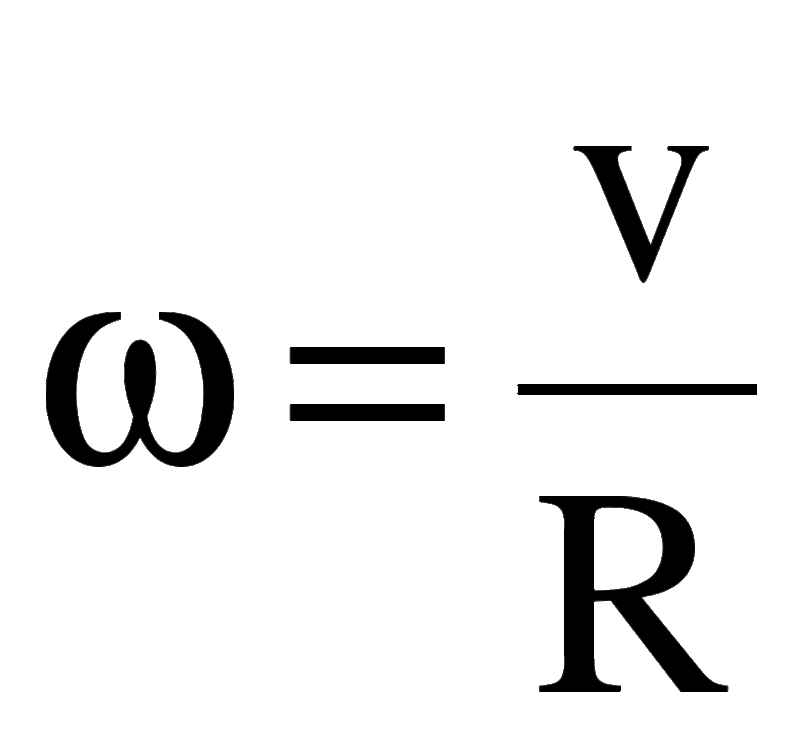 Как я представил в этом блоге, измерение угла в радианах просто означает деление длины дуги на радиус окружности.

Угол, измеряемый в радианах, представляет собой просто длину дуги, деленную на радиус

Мы можем написать, что угол, измеренный в радианах, равен

. Но линейная скорость просто определяется как расстояние, деленное на время, поэтому мы можем написать

. как

Используя это для, мы можем записать угловую скорость как

Направление вектора угловой скорости

Записав это в терминах векторов и помня, что деление векторов не определено, вместо этого мы напишем, что

, где векторное произведение (или кросс-произведение), как я обсуждал в этом блоге здесь.

Направление радиус-вектора от центра окружности, а направление линейной скорости для объекта, движущегося против часовой стрелки, соответствует направлению, показанному на диаграмме ниже, по касательной к окружности, то есть под прямым углом к радиальный вектор .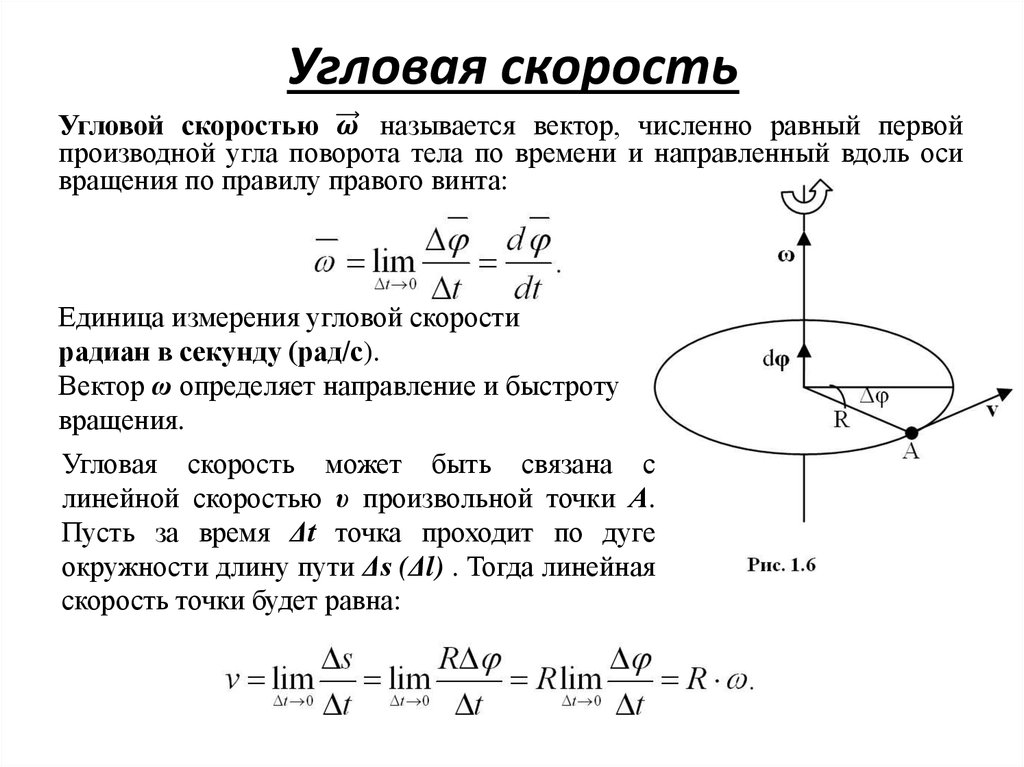

Направление радиус-вектора от центра окружности, направление линейной скорости для объекта, движущегося против часовой стрелки, как показано, под прямым углом к ​​радиус-вектору.

Чтобы найти направление , мы можем использовать правило правой руки , как показано на рисунке ниже.

Правило правой руки для определения направления результата векторного произведения

В нашем примере здесь наш первый палец находится в направлении радиального вектора, а наш второй палец находится в направлении линейной скорости, что приводит к тому, что угловая скорость (представленная большим пальцем) направлена ​​наружу или к нам, как показано на рисунке ниже.

Направление вектора угловой скорости перпендикулярно плоскости вращения объекта.

Другой способ найти это направление — обхватить пальцы правой руки в направлении вращения, тогда большой палец покажет направление вектора угловой скорости.

Направление угловой скорости также можно найти, как показано на этом рисунке.

Нравится:

Нравится Загрузка…

Рубрика: математика, физика | Метки: угловая скорость, Круговое движение, линейная скорость, Радианы, Векторный продукт | 1 комментарий

3.2.2. Угловые скорости – современная робототехника

3.2.2. Угловые скорости

• Описание
• Стенограмма

В этом видео представлены 3-векторные угловые скорости и пространство кососимметричных матриц 3 × 3, называемое so(3), алгебра Ли группы Ли SO(3). Любая 3-векторная угловая скорость имеет соответствующее представление so(3).

Предположим, что R — это матрица поворота кадра {b} относительно кадра {s}. Простая идея состоит в том, чтобы определить скорость вращения {b}, которую также называют угловой скоростью, как R-точку, скорость изменения R во времени. Но это имеет 9 переменных, и мы должны быть в состоянии найти хорошее представление угловой скорости с использованием только 3 переменных. В отличие от искривленного пространства ориентаций SO(3), представленного здесь в виде сферы при любой заданной ориентации, пространство угловых скоростей представляет собой плоское трехмерное векторное пространство, касающееся SO(3) в этой ориентации. Трехмерное векторное пространство можно представить глобально, без каких-либо особенностей, тремя координатами.

Эта система координат tinkertoy представляет собой систему координат {b}. Теперь представьте ось вращения, проходящую через начало координат, и движение фрейма, когда он вращается вокруг этой оси в соответствии с правилом правой руки.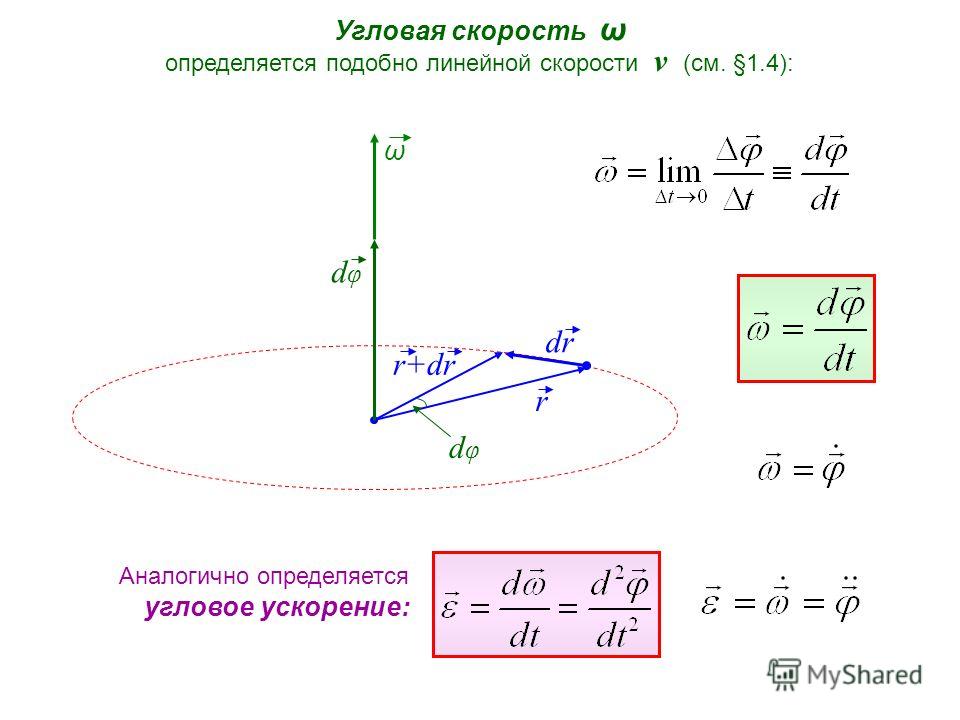 Любая угловая скорость может быть представлена ​​осью вращения и скоростью вращения вокруг нее. Мы можем выразить ось как единичный вектор в системе координат {s}, записав ее как omega-hat_s. Шляпа означает, что вектор имеет единичную длину. Мы называем скорость вращения theta-dot, и мы можем умножить единичную ось omega-hat_s на скорость вращения theta-dot, чтобы получить вектор угловой скорости omega s, выраженный в системе отсчета {s}.

При вращении кадра вокруг оси ось x b-кадра описывает окружность. Линейная скорость оси x направлена ​​по касательной к этой окружности и рассчитывается как пересечение omega_s с x-hat_b. Аналогичная зависимость справедлива и для двух других осей координат. Поскольку мы будем часто брать векторное произведение вектора с другим вектором, мы определим обозначение в квадратных скобках, которое позволяет нам записать x, скрещенное с y, как скобка-x, умноженная на y, где скобка-x представляет собой матричное представление 3 на 3 3 -вектор х. Матрица скобка-x называется кососимметричной матрицей, потому что скобка-x равна отрицательному значению ее транспонирования. Набор всех кососимметричных матриц размером 3 на 3 называется маленьким так (3) из-за его связи с большим SO (3), пространством матриц вращения.

Используя обозначение в скобках, мы можем записать отношение между R-точка и угловой скоростью omega_s как R-точка = скобка omega_s умножить на R.

Вектор угловой скорости может быть выражен в других системах отсчета, а не только в {s} Рамка. Например, мы могли бы записать это в координатах кадра {b}. Используя наше правило отмены изменения нижнего индекса опорного кадра из предыдущего видео, мы получаем, что omega-b равно R_bs, умноженному на omega_s, или обратному значению R_sb, умноженному на omega-s. R обычно указывает каркас тела относительно пространственного каркаса, поэтому мы можем опустить нижние индексы и записать взаимосвязь между угловой скоростью тела и пространственной угловой скоростью, как omega_b равно R, обратному умножению на omega_s, а omega_s равно R, умноженному на omega_b. Мы также найдем полезным небольшое матричное представление so(3) угловой скорости.