Содержание
Угловое смещение и угловая скорость: 7 важных фактов
В этой статье мы собираемся обсудить 7 важных фактов, связанных с угловым смещением и угловой скоростью.
Сообщите нам сначала о угловое смещение и угловая скорость. Предположим, что тело вращается вокруг оси. Теперь угол между его положением покоя и его положением вращательного движения известен как угловое смещение тела. Скорость изменения углового смещения известна как угловая скорость.
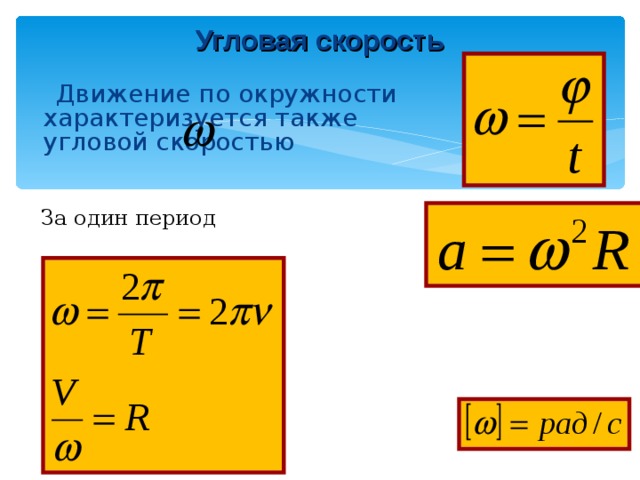
Следовательно, мы можем сказать, что и угловое смещение, и угловая скорость связаны с вращательным движением. Обычно мы обозначаем угловое перемещение через θ, а угловую скорость через ω. Единицей углового смещения в СИ является радиан и как мы это знаем
| Угловая скорость ( ω ) = изменение углового смещения (∆θ) / изменение во времени (∆t) = радиан/секунда или радиан.секунда⁻¹ |
выражение угловой скорости
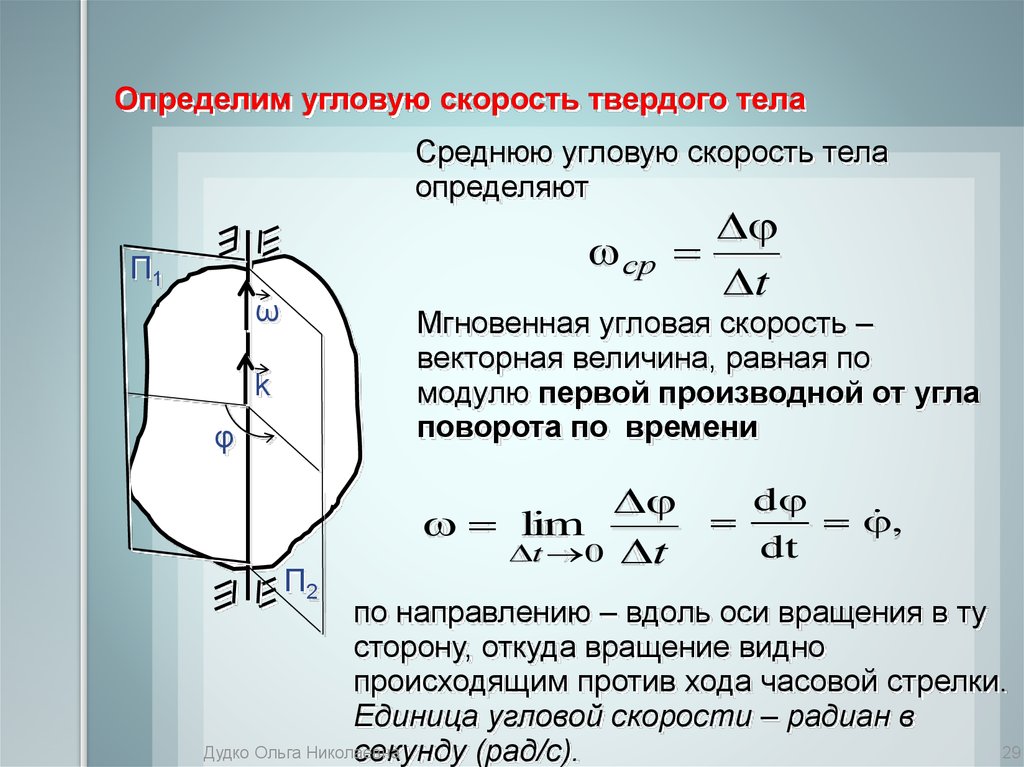
Угловое смещение имеет величину, а также определенное направление (по часовой стрелке или против часовой стрелки), поэтому это векторная величина. Точно так же угловая скорость также имеет величину и определенное направление, поэтому она также является векторной величиной.
Точно так же угловая скорость также имеет величину и определенное направление, поэтому она также является векторной величиной.
Предположим, что тело движется вокруг неподвижной оси, значит, оно продолжает свое вращательное движение. Теперь угол, образуемый между его положением покоя и положением, в котором он наконец достиг, является его угловым смещением. Если мы разделим это угловое смещение на общее время, затрачиваемое телом на достижение конечного положения, мы получим угловую скорость.
Как угловое перемещение связано с угловой скоростью?
Предположим, что тело движется вокруг неподвижной оси, значит, оно продолжает свое вращательное движение.
Теперь угол, образуемый между его положением покоя и положением, в котором он наконец достиг, является его угловым смещением. Если мы разделим это угловое смещение на общее время, затрачиваемое телом на достижение конечного положения, мы получим угловую скорость.
Возьмем дугу окружности, по которой движется тело, за s, а радиус окружности за r. Следовательно
Следовательно
| Угловое смещение = дуга окружности/радиус окружности поскольку s мало, следовательно, она считается прямой линией, т. е. нормальный sinθ = s/r Здесь θ — очень маленький угол, следовательно, sinθ ≈ θ Отсюда θ = s/r …(1) |
выражение углового смещения
Точно так же угловая скорость может быть записана как
| Угловая скорость = изменение углового смещения / изменение во времени ω = ∆θ/∆t Здесь lim ∆t → 0, следовательно, ∆θ/∆t → dθ/dt Следовательно, ω = dθ/dt ➡ ω = d/dt(s/r) [подставляя значение θ из уравнения (1), получаем ] ➡ ω = 1/r.  (ds/dt) (ds/dt) ➡ ω = v/r [так как ds/dt = v = линейная скорость] ➡ v = ωr |
связь между угловым смещением и угловой скоростью
ω = dθ/dt. Это соотношение между угловым смещением и угловой скоростью.
Могут ли угловое перемещение и угловая скорость быть одинаковыми?
Угловое смещение и угловая скорость могут быть одинаковыми.
Мы знаем, что угловая скорость = ω = dθ/dt. Если начальное угловое смещение вращающегося тела равно 0, а конечное угловое смещение этого тела равно θ, то изменение угловой скорости будет
= dθ= ( θ – 0) = θ и если время равно 0, когда угловое смещение равно 0, и время равно t=1 единице, когда угловое смещение равно θ, то dt = (t – 0) = (1-0 ) = 1 единица
Поэтому ω = dθ/dt
= θ/1
= θ
ю = θ
Отсюда доказано, что изменение углового смещения и угловой скорости одно и то же.
Как найти угловую скорость по угловому перемещению?
Угловое смещение и угловая скорость находятся в том же соотношении, что и линейное смещение и линейная скорость.
Итак, мы вычисляем линейную скорость, разделив ее на время. Точно так же мы можем получить угловую скорость, разделив угловое перемещение на затраченное время.
Предположим, что тело движется вокруг неподвижной оси, значит, оно продолжает свое вращательное движение. Теперь угол, образуемый между его положением покоя и положением, в котором он наконец достиг, является его угловым смещением. Если мы разделим это угловое смещение на общее время, затрачиваемое телом на достижение конечного положения, мы получим угловую скорость.
Угловое смещение
Возьмем дугу окружности, по которой движется тело, за s, а радиус окружности за r. Следовательно, угловое смещение = дуга окружности/радиус окружности.
поскольку s мало, следовательно, он считается прямой линией, т. е. нормальной sinθ = с/р
е. нормальной sinθ = с/р
Здесь θ — очень маленький угол, поэтому грех θ ≈ θ
следовательно θ = s / r
Точно так же угловая скорость может быть записана как
Угловая скорость = изменение углового смещения / изменение во времени
ю = Δθ/Δt
Здесь lim ∆t → 0, следовательно, ∆θ/∆t → dθ/dt
Следовательно , ω = dθ/dt
➡ ω = d/dt(s/r) [подставляя значение θ из уравнения (1), получаем ]
➡ ω = 1/r.(ds/dt)
➡ ω = v/r [так как ds/dt = v = линейная скорость]
➡ v = ωr
Разница между угловым смещением и угловой скоростью
Различия между угловым смещением и угловой скоростью записаны ниже:
| В пересчете на | Угловое смещение | Угловая скорость |
| Определение | 1.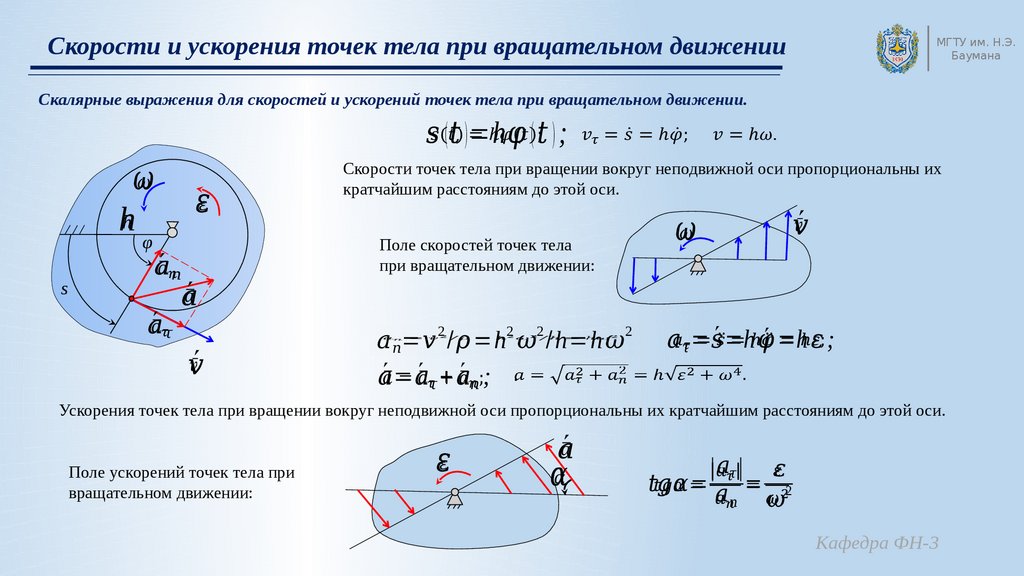 Угол между положением покоя тела и положением его вращательного движения называется угловым смещением этого тела. Угол между положением покоя тела и положением его вращательного движения называется угловым смещением этого тела. |
1. Скорость изменения углового смещения известна как угловая скорость. |
| Ед. изм | 2. Единицей углового смещения в системе СИ является радиан. | 2. Единицей угловой скорости в системе СИ является радиан/секунда. |
| Математическая формула | 3. Математическая формула для углового смещения: θ = s/r | 3. Математическая формула для угловой скорости: ω = dθ/dt |
| Размеры | 4. Это безразмерная величина. | 4. Размерность угловой скорости равна [M⁰.L⁰.T⁻¹] |
| Аналогично с | 5. Угловое смещение вращательного движения аналогично линейному смещению линейного движения. |
5. Угловая скорость вращательного движения аналогична линейной скорости линейного движения. |
Разница между Угловое смещение и Угловая скорость
График углового смещения и угловой скорости
Связь между угловым смещением и угловой скоростью
ω = dθ/dt
➡ dθ = ω.dt
Если начальное угловое смещение вращающегося тела равно 0, а конечное угловое смещение этого тела равно θ, то изменение угловой скорости будет
= dθ= ( θ – 0) = θ и если время равно 0, когда угловое смещение равно 0, и время равно t, когда угловое смещение равно θ, то dt = (t – 0) = t
Поэтому
➡ dθ = ω.dt
➡ θ = ωxt
➡ θ = ωt
Таблица данных графика между угловым смещением и угловой скоростью
| Продолжительность | угловое смещение (θ в рад) | угловая скорость ( ω в рад/с) |
| t = постоянная = 5 с | 15 | 1 |
| t = постоянная = 5 с | 10 | 2 |
| t = постоянная = 5 с | 15 | 3 |
| t = постоянная = 5 с | 20 | 4 |
| t = постоянная = 5 с | 25 | 5 |
таблица данных графика между угловым смещением и угловой скоростьюграфик между угловым смещением и угловой скоростью
Постановка задачи с решениями
- Мили гуляет по круглому парку радиусом 70 м.
 если ее линейное перемещение равно 700 м, то найти величину ее углового перемещения.
если ее линейное перемещение равно 700 м, то найти величину ее углового перемещения.
Ответ :
Радиус кольцевого парка = r = 70 м
Линейное перемещение mili = s = 700 м
Следовательно, ее угловое смещение, θ = s/r
➡ θ = 700/70 радиан
➡ θ = 10 радиан
Следовательно, угловое смещение Мили составляет 10 радиан.
- 2. Автомобиль начинает бегать вокруг круглого пруда. Если вначале он находился в покое, то его окончательное угловое перемещение через 100 секунд становится равным 20 радианам. Какова будет его угловая скорость?
Ответ :
Начальное угловое смещение, θ₁ = 0 рад
Конечное угловое смещение, θ₂ = 100 рад
Изменение углового смещения, ∆θ = θ₂ – θ₁ = (100 – 0) радиан = 100 радиан
Изменение во времени, ∆t = (20 -0) секунд = 20 секунд
Следовательно, искомая угловая скорость, ю = Δθ/Δt
➡ ω = 100/20 рад/сек
➡ ω = 5 рад/сек
Поэтому требуемая угловая скорость автомобиля равна 5 рад/сек.
Заключение
В этой статье нашей главной задачей было кратко дать ясное представление об угловом смещении и угловой скорости. Итак, начиная с определения как углового смещения, так и угловой скорости, мы попытались прояснить каждую мельчайшую деталь, связанную с ними. Помимо этого, в этой статье обсуждались разница между этими двумя величинами, график между угловым смещением и угловой скоростью и связанные с ними численные проблемы.
Узнайте больше о
| Может ли смещение быть больше, чем расстояние? Может ли смещение быть равным нулю? Перемещение и сила |
Расстояние и перемещение одинаковы? Линейное смещение и угловое смещение Направление углового смещения |
Может ли смещение быть отрицательным? Смещение в круговом движении |
definition of Угловая скорость and synonyms of Угловая скорость (Russian)
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Угловая скорость (синяя стрелка) в одну единицу по часовой стрелке
Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке
Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки
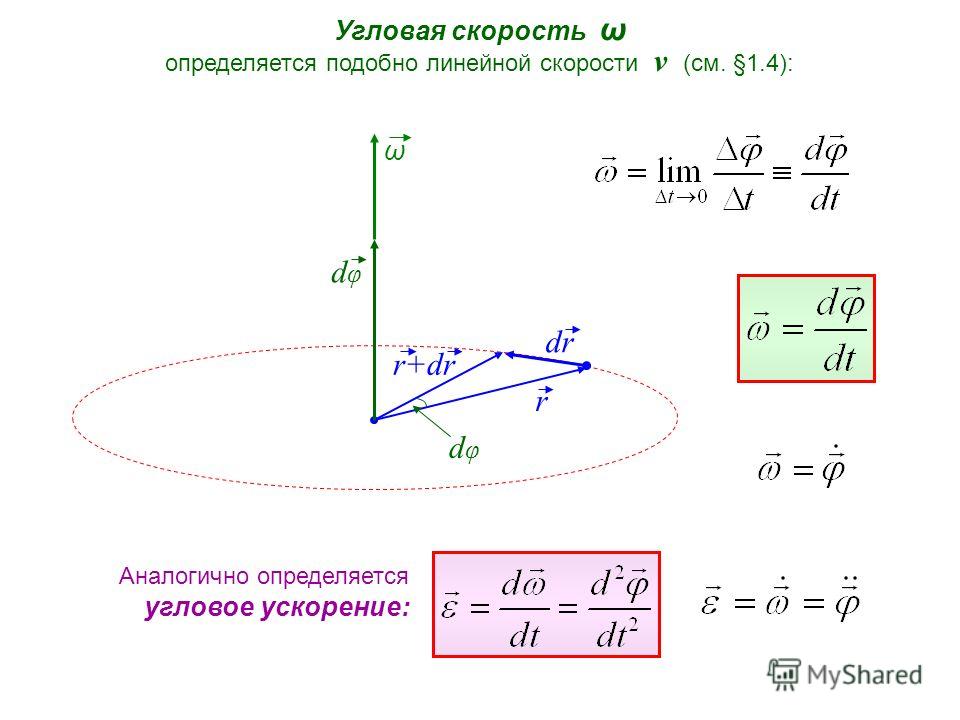
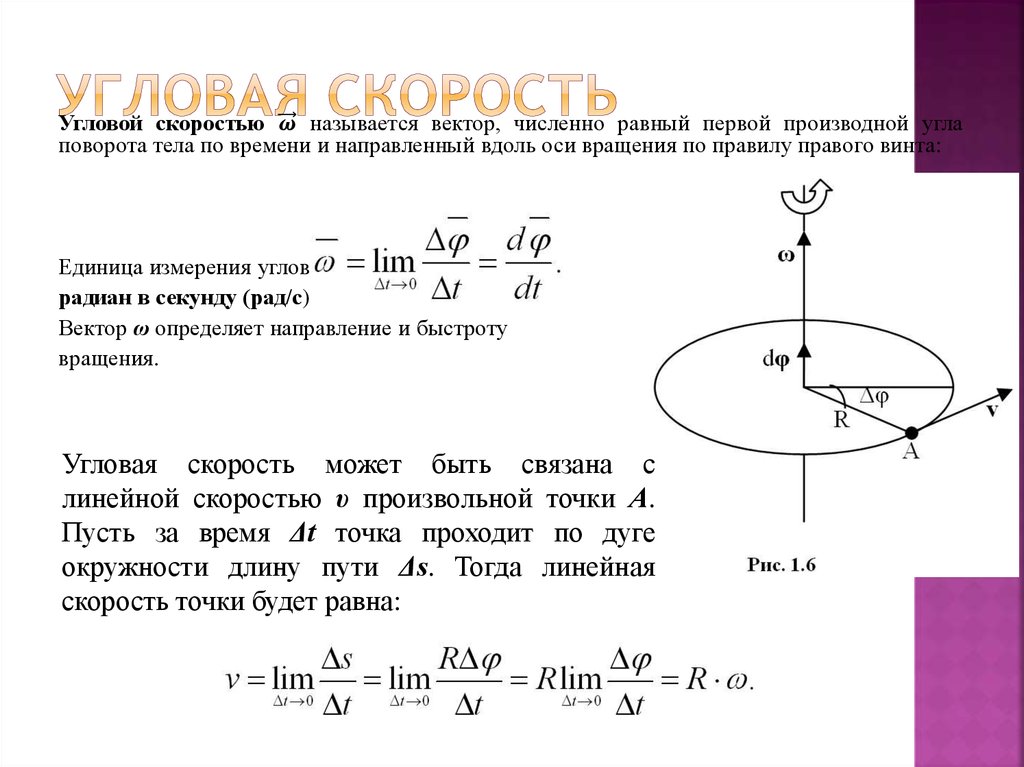
Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
- ,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.
Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:
где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
- В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
- Производная угловой скорости по времени есть угловое ускорение.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).

- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
-
, где — радиус-вектор точки (из начала координат), — скорость этой точки. — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор).
 При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
- В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.
- При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц) (то есть в таких единицах ).
- В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:
- Наконец, при использовании градусов в секунду связь с частотой вращения будет:
- Угловая частота
- Угловое ускорение
- Момент импульса
Угловая скорость Определение и значение
- Основные определения
- Викторина
- Примеры
- Британский
- Научный
Показывает уровень сложности слова.
Сохрани это слово!
Показывает уровень оценки в зависимости от сложности слова.
сущ. Физика.
Скорость изменения углового положения вращающегося тела во времени, обычно выражаемая в радианах в секунду или радианах в минуту.
ВИКТОРИНА
ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?
Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!
Вопрос 1 из 7
Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.
Происхождение угловой скорости
Впервые записано в 1810–20 гг.
Dictionary.com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
Как использовать угловую скорость в предложении
-
Однако, если они были достаточно далеко от фонарного столба, они никак не могли оставаться скрытыми — они просто не успевали за угловой скоростью, с которой, казалось, двигался фонарный столб в вашей системе отсчета.

Сможете ли вы отгадать эти загадки вне парка?|Зак Висснер-Гросс|15 октября 2021 г.|FiveThirtyEight
-
Вы тоже будете нестись под угловатые гитары и зигзагообразный отрывистый вокал.
10 лучших альбомов 2014 года: Taylor Swift, Sia, Run the Jewels и другие|Марлоу Стерн|28 декабря 2014|DAILY BEAST
-
Телефонные линии загорались от скорости и свирепости его слов.
Дэвид Гарт, консультант, который говорил с избирателями|Джефф Гринфилд|15 декабря 2014 г.|DAILY BEAST
-
Традиционные автобусные сиденья создавали иллюзию удобной набивки, но были угловатыми и не отражали формы тела.
Летающий автобус — это новый ад: как инженеры авиакомпаний устраивают вас из комнаты|Клайв Ирвинг|25 ноября 2014 г.|DAILY BEAST
-
Гутзон Борглум.
Сердце тьмы: В долину Талибана в Афганистане|Мэтт Тревитик, Дэниел Секман|15 ноября 2014 г.|DAILY BEAST
-
Вы используете топливо, чтобы задать правильную скорость и направление, а затем отключаете топливные баки и едете по инерции там.

Нил де Грасс Тайсон разбирает «Интерстеллар»: черные дыры, замедление времени и массивные волны|Марлоу Стерн|11 ноября 2014 г.|DAILY BEAST
-
Его скорость была такой, что на некоторых участках пути скорость часто 12 миль в час.
Пятьдесят лет железнодорожной жизни в Англии, Шотландии и Ирландии|Джозеф Татлоу
-
Когда вода попадает в цилиндр, кран выскакивает из своего гнезда и предотвращает любые отклонения от скорости маховика.
Жизнь Ричарда Тревитика, Том II (из 2)|Фрэнсис Тревитик
-
Он был высоким, угловатым и исхудавшим, а его черты были отлиты в самой неправильной форме.
Портсмут-роуд и ее притоки|Чарльз Г. Харпер
-
Течения обычно направляются на север и редко движутся с какой-либо скоростью на восток или запад.
Рассказ об исследовании межтропического и западного побережья Австралии] [Том 2 из 2] | Филипп Паркер Кинг
-
Конгломерат, содержащий угловатые обломки желтовато-серого кварца, в основании компактного эпидота.

Рассказ об исследовании межтропического и западного побережья Австралии] [Том 2 из 2]|Филлип Паркер Кинг
Британский словарь определений угловой скорости вращение вокруг заданной оси, измеряемое как скорость изменения угла, образуемого на этой оси траекторией bodySymbol: ω
Английский словарь Коллинза — полное и полное цифровое издание 2012 г.
© William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins
Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения угловой скорости
угловая скорость
Скорость изменения угла, связанного с объектом по отношению к некоторой контрольной точке. Например, средняя угловая скорость объекта, движущегося вокруг центральной точки отсчета один раз в секунду, составляет 2π радиан в секунду; Земля вращается вокруг своей оси с угловой скоростью 2π радиан в сутки. Также называется угловой частотой
Научный словарь American Heritage®
Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company.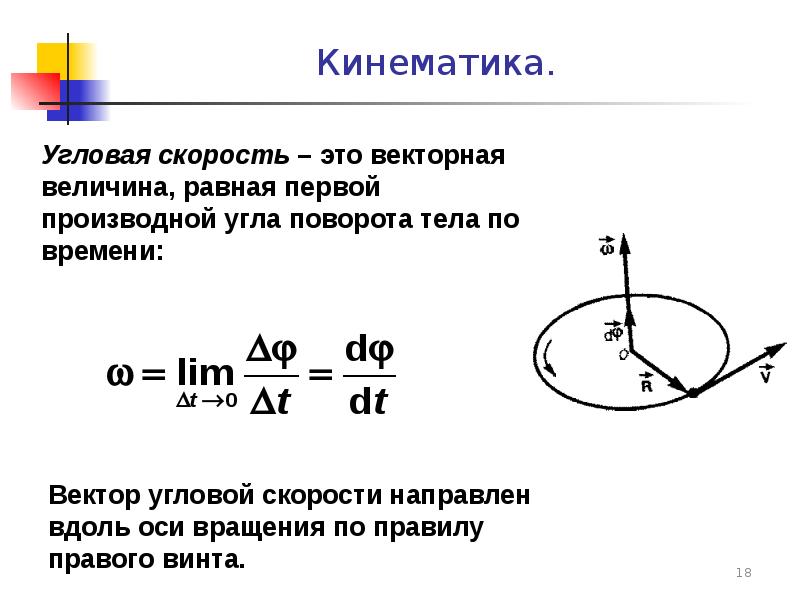 Все права защищены.
Все права защищены.
Что такое угловое ускорение (ускорение вращения)?
К
- Участник TechTarget
Угловое ускорение, также называемое вращательным ускорением, является количественным выражением изменения угловой скорости, которому подвергается вращающийся объект в единицу времени. Это векторная величина, состоящая из компонента величины и одного из двух определенных направлений или смыслов.
Величина или длина вектора углового ускорения прямо пропорциональна скорости изменения угловой скорости и измеряется в радианах на секунду в квадрате (рад/с 2 или рад · с -2 ). Альтернативно величина углового ускорения может быть выражена в градусах на секунду в квадрате (град/с 2 или град·с -2 ). Направление вектора углового ускорения перпендикулярно плоскости, в которой происходит вращение.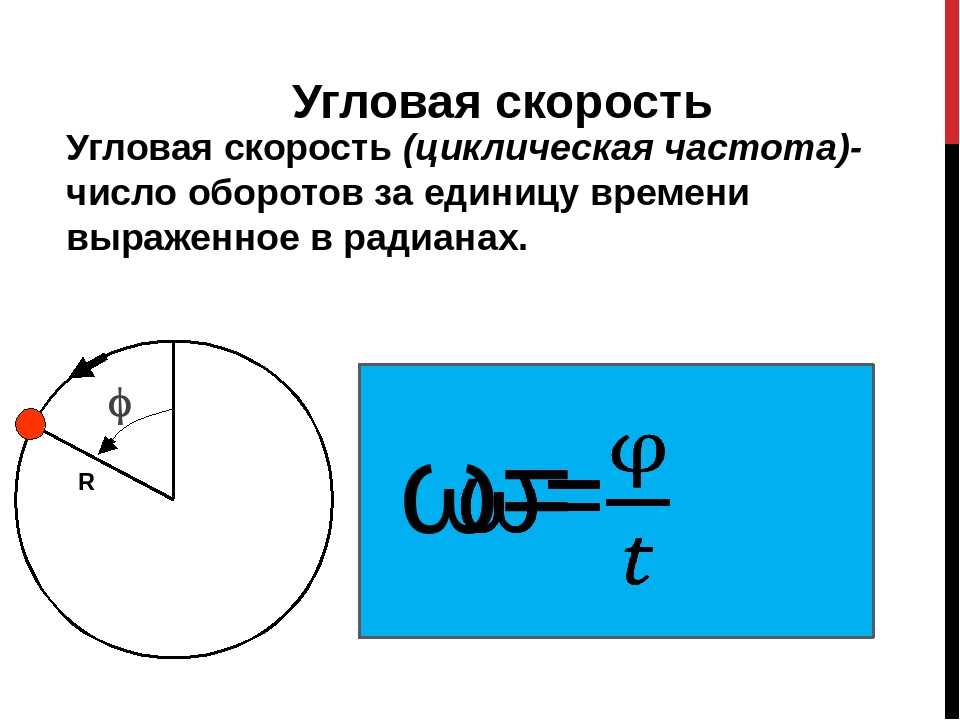 Если увеличение угловой скорости происходит по часовой стрелке по отношению к наблюдателю, то вектор углового ускорения направлен от наблюдателя. Если увеличение угловой скорости происходит против часовой стрелки, то вектор углового ускорения указывает на наблюдателя.
Если увеличение угловой скорости происходит по часовой стрелке по отношению к наблюдателю, то вектор углового ускорения направлен от наблюдателя. Если увеличение угловой скорости происходит против часовой стрелки, то вектор углового ускорения указывает на наблюдателя.
Вектор углового ускорения не обязательно указывает в том же направлении, что и вектор угловой скорости. Рассмотрим автомобиль, катящийся по шоссе с увеличивающейся скоростью. Векторы угловых ускорений для всех четырех шин направлены влево вдоль линий, содержащих оси колес. Если автомобиль перестает разгоняться и сохраняет постоянную скорость, векторы углового ускорения исчезают. Если автомобиль замедляется при движении вперед, векторы меняют свое направление и указывают вправо вдоль линий, содержащих оси колес. Если автомобиль включается задним ходом и увеличивает скорость, двигаясь назад, векторы углового ускорения указывают вправо вдоль линий, содержащих оси. Если обратная скорость постоянна, векторы углового ускорения обращаются в нуль; если обратная скорость уменьшается, векторы углового ускорения направлены влево вдоль линий, содержащих оси колес.
См. также ускорение, радиан на секунду в квадрате и градус на секунду в квадрате.
Последнее обновление: январь 2011 г.
враждебный ML
Состязательное машинное обучение — это метод, используемый в машинном обучении для обмана или введения в заблуждение модели с помощью злонамеренных входных данных.
Сеть
-
межсоединение центра обработки данных (DCI)Технология соединения центров обработки данных (DCI) связывает два или более центров обработки данных вместе для совместного использования ресурсов.
-
Протокол маршрутной информации (RIP)Протокол маршрутной информации (RIP) — это дистанционно-векторный протокол, в котором в качестве основной метрики используется количество переходов.
-
доступность сетиДоступность сети — это время безотказной работы сетевой системы в течение определенного интервала времени.

Безопасность
-
GPS-глушениеПодавление сигналов GPS — это действие устройства, передающего частоту, для блокирования или создания помех радиосвязи.
-
контрольная суммаКонтрольная сумма — это значение, представляющее количество битов в передаваемом сообщении, которое используется ИТ-специалистами для обнаружения …
-
информация о безопасности и управление событиями (SIEM)Управление информацией о безопасности и событиями (SIEM) — это подход к управлению безопасностью, объединяющий информацию о безопасности …
ИТ-директор
-
FMEA (анализ видов и последствий отказов)FMEA (анализ видов и последствий отказов) представляет собой пошаговый подход к сбору сведений о возможных точках отказа в …
-
доказательство концепции (POC)Доказательство концепции (POC) — это упражнение, в котором работа сосредоточена на определении того, можно ли превратить идею в реальность.

-
зеленые ИТ (зеленые информационные технологии)Green IT (зеленые информационные технологии) — это практика создания и использования экологически устойчивых вычислений.
HRSoftware
-
самообслуживание сотрудников (ESS)Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой …
-
платформа обучения (LXP)Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…
-
Поиск талантовПривлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …
Отдел обслуживания клиентов
-
закон убывающей отдачиЗакон убывающей отдачи — это экономический принцип, утверждающий, что по мере увеличения капиталовложений в какую-либо область норма .

 если ее линейное перемещение равно 700 м, то найти величину ее углового перемещения.
если ее линейное перемещение равно 700 м, то найти величину ее углового перемещения.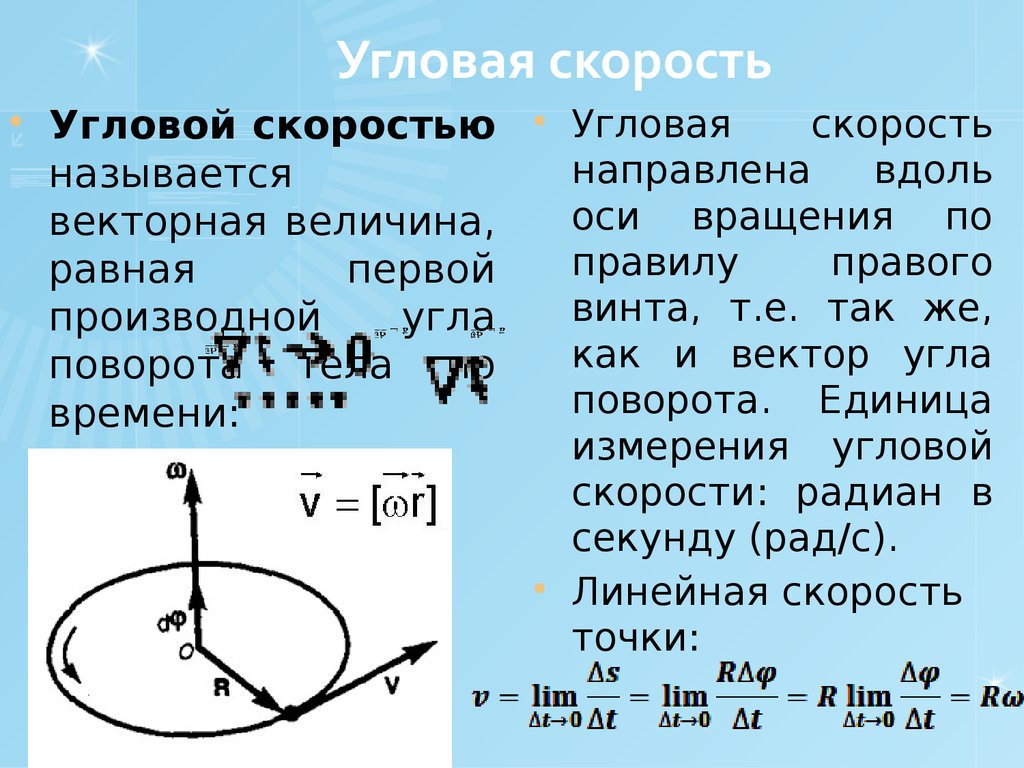
 При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.