Содержание
5 ответов, которые вы должны знать
Тело, которое периодически движется вперед и назад, называется колеблющимся телом, и это движение — колебание.
Когда тело колеблется, оно перемещается линейно, но помимо этого существует еще и угловая частота колебаний. Давайте проанализируем угловую частоту и частоту. Угловая частота — это не что иное, как изменение угла тела. В концепции физики угловая частота и частота различны.
Не следует путать угловую частоту и линейную частоту колебания. Их двое
разные концепции с разным использованием. Угловая частота определяет изменение фазы, тогда как линейная частота указывает количество колебаний, совершаемых за секунду.
Чтобы изучить зависимость угловой частоты от частоты, возьмем пример качелей в детском парке. Он продолжает качаться взад и вперед через равные промежутки времени. Следовательно, это колебательное движение. Из приведенного выше рисунка видно, что качели движутся вперед под углом θ и также возвращаются на тот же угол. Изменение угла, происходящее в единицу времени, является угловой частотой колебаний.
Изменение угла, происходящее в единицу времени, является угловой частотой колебаний.
ω=2π/T
Количество раз, когда он перемещается вперед и назад за одну секунду, будет частотой качания.
Колебание — это простые гармонические колебания, и, следовательно, его уравнение такое же, как у синусоидальной волны
уравнение.
Для колеблющегося объекта уравнение SHM имеет вид:
Здесь;
x — смещение объекта
A — амплитуда колебаний
φ — изменение фазы
ω — угловая частота
Предположим, на веревке свисает маленький боб. Когда мы ударяем по бобу, он начинает двигаться и колебаться.
Из приведенной выше схемы свободного тела видно, что боб смещается под углом. Отсюда угловой
частота задается как:
ω=2π/T
В то же время частота качания будет колебанием, совершаемым за 1 секунду. Предположим, здесь он совершает 5 колебаний за одну секунду. Тогда частота боба равна 5.
Угловая частота против частоты
На рисунке выше хорошо видна разница между угловой частотой колебаний и частотой колебаний.
Частота. Общая формула для расчета частоты колебаний f имеет следующий вид:
f=1/Т
Здесь T — период времени.
Формула угловой частоты колебаний:
ω=2π/T
Подставляя значение T из частотной формулы в формулу угловой частоты, мы
получать;
ω = 2πf
Это дает связь между частота и угловая частота колебаний. Формула угловой частоты вычисляется путем умножения частоты на угол, который покрывает колеблющийся объект. Для полного цикла угол равен 2π.
Изображение Фото: Мормегил, Маятник, CC BY-SA 3.0
Для простого маятника угловая частота и линейная частота задаются как:
И,
Изображение Фото: https://en.wikipedia.org/wiki/Wilberforce_pendulum#/media/File:Wilberforce_pendulum_oscillation_modes.svg
Для пружины формула угловой частоты и линейной частоты имеет следующий вид:
и
Единица угловой частоты выражается в радианах в единицу времени, то есть:
1ω=1рад.сек-1
Стандартной единицей измерения частоты колебаний является Герц, Гц.
Предположим, мяч колеблется и совершает 6 колебаний за 1 секунду. Тогда частота колебательного шара будет:
f=6 Гц
И поэтому угловая частота становится:
ω=2π*6
ω = 12π
Часто задаваемые вопросы (FAQ)
Что такое колебание?
В физике, когда объект со временем смещается со своего места, он находится в движении.
Объект, который периодически движется вперед и назад, известен как колеблющееся тело, и это движение колебание. Все колебания периодические, но обратное может быть неверным. Земля вращается вокруг Солнца периодически, но не колебательно.
Какие термины относятся к колебаниям?
Тело, движущееся в непрерывном партнере вокруг неподвижной точки, является колебательным.
Колебательное тело имеет уравнение:
Вот общие условия колебаний:
x обозначает смещение объекта
A — его амплитуда
φ — изменение фазы
ω — угловая частота
Частота — важный термин колебаний, который говорит о количестве колебаний, совершенных за одно.
второй.
Как найти угловую частоту простого маятника?
Маятник — это простое колеблющееся тело, на веревке которого свисает груз массой.
Когда маятник колеблется, он меняет угол через равные промежутки времени. Следовательно, простой маятник имеет угловое смещение. Угловая частота колебания маятника рассчитывается по формуле:
здесь
g — ускорение свободного падения, а
L — длина маятника.
В чем разница между угловой частотой и линейной частотой?
Угловая частота сильно отличается от линейной частоты. Оба имеют разные значения.
Когда тело колеблется, его угол, который является угловой частотой, изменяется.
Количество колебаний частицы за одну секунду — это частота объекта. В
единица угловой частоты в рад / сек. Единица измерения частоты Герц.
Какая связь между линейной частотой и угловой частотой колебаний?
Когда тело непрерывно движется между двумя точками, говорят, что оно находится в колебательном движении. Частота и угловая частота связаны друг с другом из заданного
Частота и угловая частота связаны друг с другом из заданного
формула:
Формула для частоты и угловой частоты: f=1/T и ω=2π/T
Подставляя значение T, получаем:
ω = 2πf
Циклическая частота, теория и онлайн калькуляторы
Циклическая частота, теория и онлайн калькуляторы
Определение циклической частоты
Определение
Циклической (угловой, радиальной круговой) частотой называют скалярную физическую величину, которая служит
мерой вращательного или колебательного движения.
Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Циклическая частота гармонических колебаний
Колебательные движения играют важную роль в самых разных вопросах физики. Рассмотрим колебания материальной точки. При колебаниях материальная точка через равные промежутки времени проходит через одно и то же положение при движении в одном направлении.
Самым важным колебательными движениями являются гармонические колебания. Сущность таких колебаний проще всего рассмотреть на следующей кинематической модели. Путь точка M со скоростью ($v$) постоянной по величине движется по окружности радиуса A. При этом ее угловая скорость равна ${\omega }_0=const$ (рис.1).
Проекция точки на диаметр окружности, например на ось X, совершает колебания от $N_1$ до $N_2\ $и обратно (точка N). Такое колебание N ,будет называться гармоническим. Для его описания следует записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол ${\varphi }_0$. Через некоторый промежуток времени этот угол получит приращение ${\omega }_0t$ и станет равен ${\omega }_0t+{\varphi }_0$, тогда:
\[x=A{\cos \left({\omega }_0t+{\varphi }_0\right)\ }\left(1\right).\]
Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.
Рассмотрим формулу (1). Параметр $A$ — максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), амплитуда колебаний.
Параметр $A$ — максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), амплитуда колебаний.
Величина ${\omega }_0$ — циклическая частота колебаний. $\varphi =({\omega }_0t+{\varphi }_0$) — фаза колебаний; ${\varphi }_0$ — начальная фаза колебаний. Циклическую частоту гармонических колебаний определим как частную производную от фазы колебаний по времени:
\[{\omega }_0=\frac{?\varphi }{\partial t}=\dot{\varphi }\left(2\right).\]
Если начальная фаза колебаний равна нулю, то
\[x=A{\cos \left({\omega }_0t\right)\ }\left(3\right).\]
При $\varphi =\frac{\pi }{2}$ :
\[x=A{{\rm s}in \left({\omega }_0t\right)\ }\left(4\right).\]
Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ — это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.
Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.
Период (T) колебаний и циклическая частота связаны формулой:
\[{\omega }_0=\frac{2\pi }{T}\left(5\right).\]
Циклическую частоту с частотой $\nu$ связывает выражение:
\[{\omega }_0=2\pi \nu \ \left(6\right).\]
Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:
\[\left[{\omega }_0\right]=\frac{рад}{с}.\]
Размерность циклической частоты:
\[{\dim \left({\omega }_0\right)=\frac{1}{t}.\ }\]
Примеры задач с решением
Пример 1
Задание. Какова циклическая частота гармонических колебаний точки, которые происходят по оси X, если амплитуда колебаний $A=$15 см; максимальная скорость колебаний точки $v_{max}=45\frac{см}{с}$.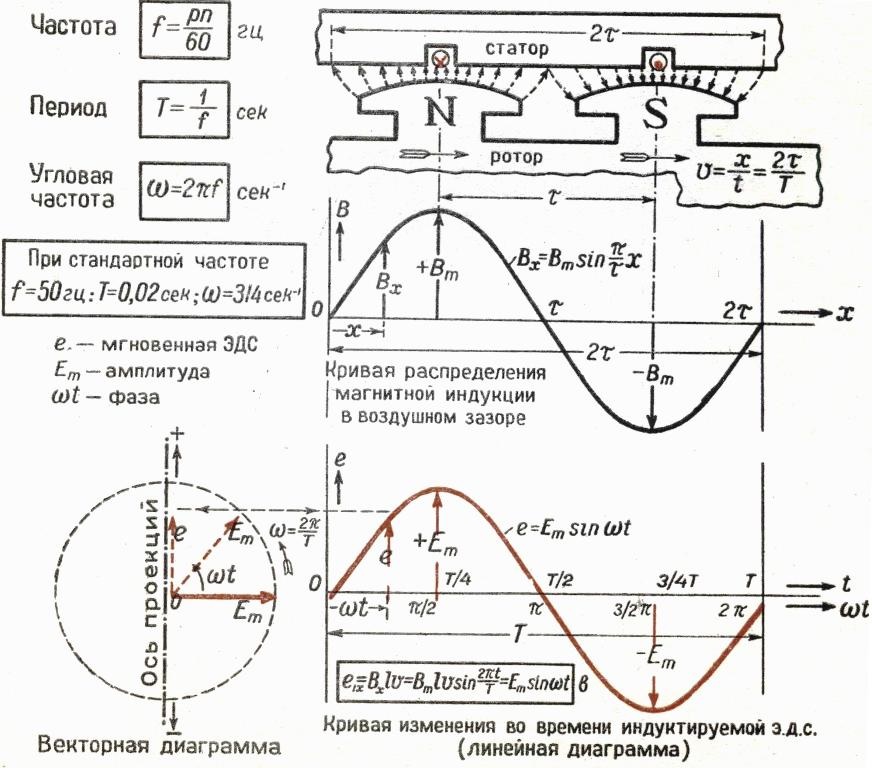
Решение. Запишем уравнение гармонических колебаний точки, если известно, что они происходят по оси X:
\[x=A{\cos \left({\omega }_0t+{\varphi }_0\right)\ }\left(1.1\right).\]
Скорость этих колебаний найдем, используя (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:
\[v=\frac{dx}{dt}=-A{\omega }_0\left({\cos \left({\omega }_0t+{\varphi }_0\right)\ }\right)\left(1.2\right).\]
Максимальное значение скорости (амплитуда скорости) равна:
\[v_{max}=Aщ_0\ \left(1.3\right).\]
Следовательно, циклическую частоту колебаний находим как:
\[{\omega }_0=\frac{v_{max}}{A}.\]
Вычислим величину циклической частоты:
\[{\omega }_0=\frac{45}{15}=3\ (\frac{рад}{с}).\]
Ответ. ${\omega }_0=3\frac{рад}{с}$
Пример 2
Задание. 2_0\to {\omega }_0=\sqrt{\frac{k}{m}}.\]
2_0\to {\omega }_0=\sqrt{\frac{k}{m}}.\]
Ответ. ${\omega }_0=\sqrt{\frac{k}{m}}$
Читать дальше: гидростатика.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
3 Важные пояснения – Lambda Geeks
Угловая частота и частота – это величины, которые измеряют колебание в единицу времени. В статье рассматривается связь между угловой частотой и частотой.
Угловая частота описывает угловое смещение тела в единицу времени. В соотношении частота описывает количество колебаний тела в единицу времени . Угловая частота измеряет ту же характеристику, что и частота, и обе величины являются скалярами, которые имеют только величину, но не направление.
Колеблющееся тело или осциллятор означает, что тело совершает периодическое движение, совершая один цикл; когда он проходит через диапазон позиций из своего среднего положения и снова возвращается в свое среднее положение.
Величины колеблющегося тела, такие как угловая частота, обозначенная символом омега ( ω ), и частота, представленная ( f ), описывают скорость колебаний тела или насколько сильно оно колеблется от своего среднего позиция . Но эти величины основаны на типах колебаний. Когда колебание является линейным, мы исследуем его частоту. Тогда как, когда он угловой, мы исследуем его угловую частоту.
Угловая частота и частота
Поскольку частота рассчитывает количество колебаний всего тела в единицу времени, единицей измерения частоты является колебаний в секунду или, точнее, циклов в секунду . Проще говоря, его единица измерения Герц(Гц) , что соответствует одному циклу в секунду.
Чтобы определить частоту колебаний, нам сначала нужно узнать его период времени. Период времени также является количеством колеблющегося тела, которое показывает общее время, затраченное телом на совершение одного колебания . Сравнивая определения как периода времени, так и частоты, эти величины колебаний обратны друг другу.
Сравнивая определения как периода времени, так и частоты, эти величины колебаний обратны друг другу.
т. е. [латекс]f = \frac{1}{T}[/latex] ……….. (#)
Например, в синусоидальной форме волны время, необходимое волне для совершения одного колебания, составляет ½ секунды, тогда ее частота составляет 2 цикла в секунду или Герц.
Угловая частота и частота
Связь между частотой и периодом времени
Но когда тело совершает угловые колебания, его смещение от среднего положения измеряется угловой частотой. Тело движется по окружности, прохождение определенного угла признается его угловым перемещением. Поскольку угловое перемещение включает в себя угол, угловая частота колеблющегося тела выражается в радиан в секунду (рад с-1) или оборотов в минуту ( об/мин).
Например, при обсуждении вращения карусели в детском парке мы выразили ее угловую частоту в радианах в минуту. Но когда речь идет об угловой частоте вращения Луны вокруг Земли, имеет смысл выражать ее в радианах в сутки.
Подробнее о Простое гармоническое движение с угловой частотой.
Связь между частотой и угловой частотой
Частота и угловая частота колеблющегося тела связаны друг с другом, поскольку обе величины используются для определения скорости колебаний тела.
Формула угловой частоты (ω) колеблющегося тела является произведением частоты (f) и угла, на который тело колеблется. т. е. [латекс]\омега = 2\pi f[/латекс]. Это означает, что угловая частота аналогична частоте с постоянным коэффициентом 2π.
Угловая частота и частота
Простое гармоническое движение (SHM) системы показывает, что угловая частота ω и частота f имеют одинаковые размерности. Следовательно, обе величины измеряются одной и той же единицей обратной времени. т. е. с-1. Этот факт согласуется с единицей измерения угловой частоты. Тем не менее, это сравнивается с законами физики и устраняет разницу в соотношении между угловой частотой и частотой. т. е. [латекс]\омега = 2\pi f[/латекс].
т. е. [латекс]\омега = 2\pi f[/латекс].
Как и частота (f) колеблющегося тела, его угловая частота (ω) также связана с периодом времени (T). Когда тело вращается по орбите или просто по окружности, его период времени оценивает общее время, необходимое телу, чтобы совершить один оборот.
Поскольку f =1/T, отношение между угловой частотой и частотой становится [латекс]\омега = \фрак{2\пи }{Т}[/латекс]. ……(*)
Связь между угловой частотой и частотой (кредит: числовой)
Что такое 2π в угловой частоте и частоте?
Когда мы выражаем скорость колебаний через период времени, постоянный коэффициент 2π связывает угловую частоту с частотой.
При описании угловой частоты мы объясняем вращение тела в радианах в секунду. Тело должно повернуться на 360°, чтобы совершить одно колебание. Поскольку 360° = 2π. Вот почему постоянный коэффициент 2π вступает в игру при связывании угловой частоты с частотой во время колебаний.
При колебании тела от среднего положения мы просто видим насколько изменяется угол колебания, на который колеблется тело, за одну секунду. Например, если угол, под которым колеблется тело, изменяется от 0 радиан до 2π радиан ( 360°) за одну секунду, мы можем определить его угловую частоту, разделив изменение угла 2π на период времени T в одну секунду. по формуле (*).
Если [латекс]\omega = \frac{2\pi }{T}[/latex] и [latex]f = \frac{1}{T}[/latex]
Тогда [латекс]\omega = 2\pi f[/латекс] 9{\ circ} [/латекс].
Подробнее о Уравнение движения по углу .
Агмальная частота против частоты
.
| Угловая частота | Частота |
| 559 | |
| 559 | |
| 5559 | |
| Число колебаний тела в единицу времени. | |
| Он использует радианы для измерения частоты колебаний. | Он использует циклы для измерения частоты колебаний. |
| Анализируется при угловых колебаниях тела. | Анализируется, когда колебания тела линейны. |
| Это угловая кинематическая величина, которая объясняется с использованием только полярной системы координат. | Это линейная кинематическая величина, которая объясняется с использованием как полярной, так и декартовой системы координат. |
| Его концепции относятся к оптике, механике и переменным цепям | Его концепции относятся к акустическим, электромагнитным и радиотехнологиям. |
выборка — Какая связь между угловой частотой и нормализованной угловой частотой
спросил
Изменено
3 года, 10 месяцев назад
Просмотрено
2к раз
$\begingroup$
Это слайд из моих конспектов лекций:
Мой профессор использовал следующие слова: «Мы обозначаем цифровые частоты заглавными буквами, а аналоговые частоты строчными буквами». наоборот, то есть
наоборот, то есть
$$\omega = \Omega T_S$$
Например, здесь
Мой профессор ошибается?
- выборка
- частота
- нормализация
$\endgroup$
1
$\begingroup$
Опять же, здесь нет правильного или неправильного. В книге Алана Оппенгейма Discrete-Time Signal Processing обозначения следующие:
- , когда есть только сигналы непрерывного времени, мы используем $\omega$ для частоты радиан в секунду.
- когда есть только сигналы с дискретным временем, мы используем $\omega$ для радианов на частоту дискретизации
- , когда присутствуют оба типа сигналов (как при выборке ), мы используем $\Omega$ для непрерывного времени в радианах на секунду частоты и $\omega$ для дискретного времени в радианах на частоту дискретизации.

