Содержание
Угловая скорость. Связь векторов линейной и угловой скоростей.
|
КАТЕГОРИИ: Археология
ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления
|
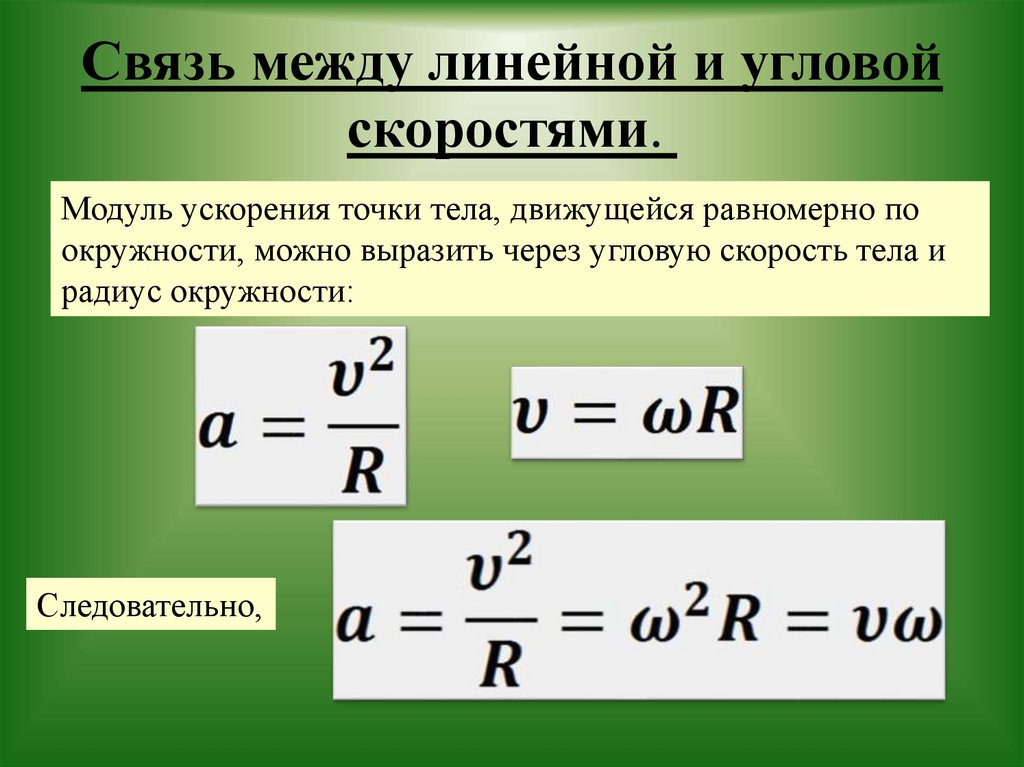
Стр 1 из 3Следующая ⇒ Угловая скорость. Связь векторов линейной и угловой скоростей. Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени: Легко найти связь между линейной скоростью точки v, ее угловой скоростью ω и радиусом r окружности, по которой она движется. т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности. При вращательном движении действуют: тангенциальное и центростремительное ускорения. В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Центробежное ускорение можно вычислить по формуле: Угловое ускорение. Связь линейных и угловых величин. Угловое ускорение — физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела. Существует связь между тангенциальным и угловым ускорениями: где R — радиус кривизны траектории точки в данный момент времени Тангенциальное ускорение направлено по касательной в траектории движения тела, а нормальное — перпендикулярно ему. 13. Сформулируйте первый закон Ньютона. Что такое замкнутая механическая система. Замкнутая механическая система, потенциальная энергия которой имеет минимальное значение и в которой отсутствуют движения тел, находится в состоянии равновесия. Примером может служить тяжелый шар, неподвижно; лежащий на дне ямы: его потенциальная энергия Ер имеет минимальное значение, и он находится в равновесии; без воздействия извне шар не может выкатиться из ямы. 20. Радиус-вектор, скорость, импульс, закон движения центра масс. Скорость — физическая величина, характеризующая движение тела в пространстве. Физический смысл — Изменение координаты в единицу времени. Импульс тела — это векторная величина, равная произведению массы тела на его скорость: . Воспользовавшись законом изменения импульса, получим закон движения центра масс: dP/dt = M∙dVc/dt = ΣFi Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы. Энергия и работа. В чём разница? Термин «работа» в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа — физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением: А = Fs cos a. Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). 1 джоуль — это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину «мощность». Мощность равняется отношению совершенной работы ко времени, за которое она выполнена: Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт — мощность, при которой совершается работа в 1 Дж за 1 секунду. Сформулируйте закон Гука. Закон Гука — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским учёным Робертом Гуком. Закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях. Угловая скорость. Связь векторов линейной и угловой скоростей. Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени: Легко найти связь между линейной скоростью точки v, ее угловой скоростью ω и радиусом r окружности, по которой она движется. т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности. При вращательном движении действуют: тангенциальное и центростремительное ускорения. В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением. Центробежное ускорение можно вычислить по формуле: 123Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 4475; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.
|
угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением
Вращательным
называют такое движение, при котором
все точки тела движутся по окружностям,
центры которых лежат на одной кривой,
называемой осью вращения (рис.1.9).Ось
вращения может находиться как внутри
(рис.1.9.а), так и вне тела (рис.1.9.б).
Поворот
тела на некоторый угол
можно задать в виде отрезка, длина
которого,
а направление совпадает с осью вращения.
Для того, чтобы указать, в какую сторону
совершается поворот вокруг данной оси,
связывают направление поворота и
изображающего его отрезка правилом
правого винта: направление отрезка
должно быть таким, чтобы, глядя вдоль
него, мы видели поворот совершающимся
по часовой стрелке (рис.1.10). Вектор
поворотаявляется не истинным вектором, а
псевдовектором.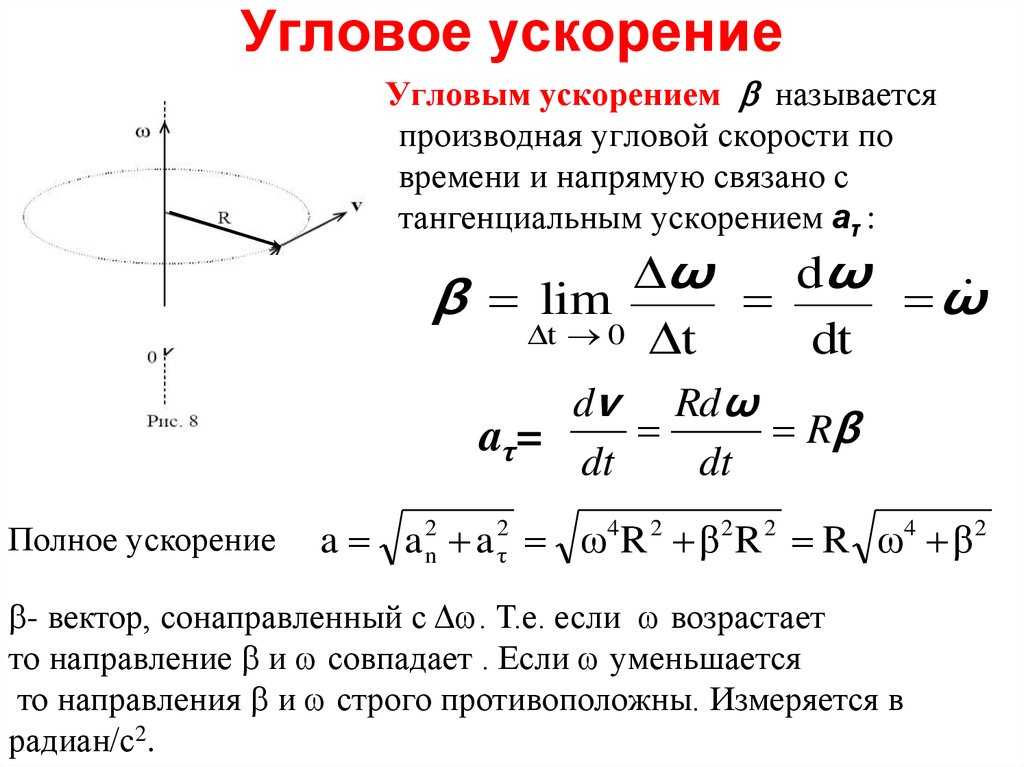
Векторная
величина
,
где
–время, за которое совершается поворот,
называется угловой скоростью тела. Она
направлена по оси вращения в сторону,
определяемую правилом правого винта,
и представляет собой псевдовектор.
Модуль угловой скорости равен.
Вращение
с постоянной угловой скоростью называют
равномерным. Такое движение характеризуют
периодом
,
под которым понимают время полного
оборота. При этом,
тогда,
и.
Число оборотов в единицу времени
( частота обращения) равно.
Подставив,
получаем:.
Вектор
может изменяться как при изменении
скорости вращения тела вокруг оси ( по
величине), так и при повороте оси вращения
в пространстве ( в этом случаеменяется по направлению). Изменение
вектора угловой скорости со временем
характеризуется угловым ускорением.
Угловое ускорение, также как и угловая
скорость, является псевдовектором.
Отдельные
точки вращающегося тела имеют различные
линейные скорости
.
Скорость каждой из точек непрерывно
изменяет свое направление. Величина
Величина
скоростиопределяется угловой скоростью вращения
телаи расстояниемрассматриваемой
точки от оси вращения. Пусть за малый
промежуток времени тело повернулось
на угол(рис.1.11). Точка, находящаяся на расстоянииот оси, проходит при этом путь.
Линейная скорость точки равна.
(1.9)
Эта
формула связывает модули линейной и
угловой скоростей. Найдем выражение,
связывающее векторы
и.
Положение рассматриваемой точки тела
будем определять радиус-вектором,
проведенным из лежащего на оси вращения
начала координатО
( рис.1.12). Из рисунка видно, что векторное
произведение
совпадает по направлению с вектороми имеет модуль, равный.
Следовательно,.
Нормальное
ускорение точек вращающегося тела равно
.
Если
ввести перпендикулярный к оси вращения
вектор
,
проведенный в данную точку тела
(рис.1.12), это выражение можно записать
в векторной форме
.
Знак минус поставлен, так как векторы
и
направлены противоположно.
Будем
считать, что ось вращения не поворачивается
в пространстве.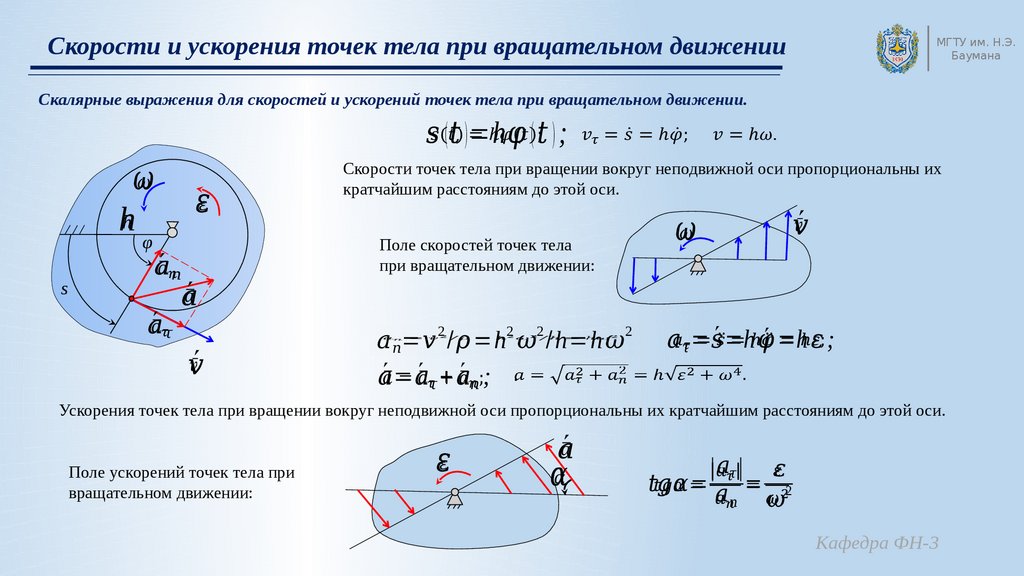 В этом случае расстояние
В этом случае расстояние
рассматриваемой точки до оси вращения
не меняется,
,
и, взяв производную от выражения (1.9),
получаем
Таким образом,
нормальное и тангенциальное ускорения
растут линейно с увеличением расстояния
точки от оси вращения.
В
случае сложного вращения, когда тело
движется одновременно относительно
нескольких осей, необходимо производить
сложения угловых скоростей. Рассмотрим
движение твердого тела, вращающегося
одновременно вокруг двух пересекающихся
осей. Сообщим некоторому телу вращение
с угловой скоростью
вокруг осиОА
(рис.
1.13) и затем эту ось приведем во вращение
с угловой скоростью
вокруг осиOB,
неподвижной
в К-системе
отсчета. Найдем результирующее
движение тела в К-системе.
Введем
вспомогательную K‘-систему
отсчета, жестко связанную
с осями ОА
и
ОВ.
Ясно,
что эта система вращается с угловой
скоростью
,
и тело вращается относительно нее с
угловой скоростью.
За
промежуток времени
тело совершит поворотвокругоси
АО
в
K‘—
системе и одновременно поворот
вокруг оси ОВ
вместе
с K‘-
системой. Суммарный поворот есть
=
+
.
Разделив обе части этого равенства на
получим
.
Таким
образом, результирующее движение
твердого тела в K—
системе представляет собой чистое
вращение с угловой скоростью
вокруг оси, совпадающей в каждый момент
с вектором
и проходящей через точкуO
(рис. 1.13). Эта ось перемещается
относительно K—
системы — она поворачивается с угловой
скоростью
вместе с осью ОА
вокруг
оси ОВ.
Нетрудно
сообразить, что даже в том случае, когда
угловые скорости
и
не
меняются по модулю, тело будет обладать
в K—
системе угловым ускорением
,
направленным, согласно,
за плоскость (рис. 1.13).
И
последнее замечание. Поскольку вектор
угловой скорости
удовлетворяет основному свойству
векторов — векторному сложению,
можно представить как векторную сумму
составляющих
на определенные направления, т. е.
е.
=++…,
где
все векторы относятся к одной и той же
системе отсчета. Этим
удобным и полезным приемом часто
пользуются при анализе
сложного движения твердого тела.
ньютоновская механика. Может ли кто-нибудь показать интуитивное соотношение между линейной и угловой скоростью?
спросил
Изменено
1 год, 9 месяцев назад
Просмотрено
545 раз
$\begingroup$
Я знаю письменный вывод $v=rω$, мы просто дифференцируем $∆s$ и $r∆\theta$, но может кто-нибудь дать интуитивный вывод.
- ньютоновская механика
- угловой момент
- вращательная динамика
- импульс
$\endgroup$
5
$\begingroup$
Думаю, было бы полезно рассмотреть случай равномерного кругового движения . ОП уже знает о своем общем происхождении через дифференциацию , но равномерное круговое движение может помочь развить некоторые интуиция .
ОП уже знает о своем общем происхождении через дифференциацию , но равномерное круговое движение может помочь развить некоторые интуиция .
Предположим, что объект совершает круговое движение с постоянной угловой скоростью $\omega$ и, следовательно, с постоянной скоростью $v$. Полный угол равен $2 \pi$, поэтому мы можем утверждать:
$$\omega = \frac{2 \pi}{T} \ \ \ \ (1)$$
, где $T$ — период времени для одного революция.
Длина окружности равна $2 \pi R$, поэтому скорость можно представить как:
$$v= \frac{2 \pi R}{T} \ \ \ \ (2)$$`
Подставляя $(2)$ в $(1)$, получаем
$$\omega = \frac{v}{R}$$
Теперь, когда мы вывели это уравнение, мы замечаем, что хотя $\omega$ говорит нам о скорости покрытия угла в радианах, умножив ее на $ R$ приводит нас к скорости, с которой прослеживается окружность.
$\endgroup$
$\begingroup$
Вы можете записать скорость в см/с, или м/с, или км/ч. .. например, физическая скорость $v$ может быть выражена как
.. например, физическая скорость $v$ может быть выражена как
$$
v = v_{км/ч} \, \frac{km}{h}= v_{м/с} \, \frac{m}{s}= v_{L/T} \, \frac{L}{ Т}
$$
, где $L$ и $T$ — общие величины длины и времени, а $v_{L/T} $ — это «значение» $v$, когда вы берете $L$ и $T$ в качестве единиц измерения.
Если вы находитесь на окружности радиуса $R$, то у вас есть естественная единица длины, $R$, и естественная единица времени, период $P$. Возьмем $T=s$ за обычную «секунду», тогда
$$ v = \frac{2 \pi R}{P} = v_{R/P} \frac{R}{P} =
v_{R/s} \frac{R}{s}$$
Здесь $v_{R/s} $ — угловая скорость (скорость, измеренная в «натуральных» единицах, всегда равна $v_{R/P} = 2 \пи$).
Для неравномерного движения по окружности — то же самое, только надо работать с производными по времени. То же самое работает и для некругового движения, но вы должны аппроксимировать траекторию локально кругом (путем расширения траектории Тейлором) или выбрать «полюс» для измерения угловой скорости.
$\endgroup$
$\begingroup$
Простой ответ
Из геометрии вы знаете, что длина дуги равна $s = r\, \theta$, где $r$ — радиус дуги, а $\theta$ — угол, на который она опирается.
Возьмите производную по времени от приведенного выше, поскольку дуга описывает движение частицы, движущейся на вращающемся теле, и вы получите $$v = r \, \omega $$, где $\omega = \frac{\rm d}{ {\rm d}t} \тета$. Также $r$ является плечом момента движения, так как мгновенно оно постоянно (остается фиксированным в значении на малых временных интервалах).
Глубокое понимание
Надеюсь, вы знакомы с векторами, потому что на этом уровне кинематика (наука о движении) становится более интуитивной, чем на уровне компонентов. В частности, вы должны быть знакомы с понятием перекрестного произведения и скалярного произведения между двумя векторами. Более важно, что выражение вида $\text{(position)}\times\text{(something)}$ знакомит нас с концепцией плеча рычага.
Вместе с рычагом появляется концепция момент . Где крутящий момент — это момент силы $\vec{\tau} = \vec{r} \times \vec{F}$, а поступательная скорость — это момент вращения $\vec{v} = \vec{r} \ раз \vec{\omega}$.
Давайте поговорим о скорости вращения (векторе) $\vec{\omega}$
Я буду использовать три различных аспекта движения, чтобы говорить о скорости вращения.
[Кинематика] $\vec{\omega}$ — математический инструмент для упрощения описания движения твердого тела. Вместо указания векторов скорости в каждой точке тела , скорость вращения позволяет нам провести удобный расчет, используя скорость одной точки для оценки скорости всех других точек $$ \vec{v}_{\rm point} = \vec{v }_{\rm ref} + \vec{\omega} \times \vec{r} $$
[Векторное поле] $\vec{\omega}$ трудно визуализировать, потому что его можно непосредственно измерить по наблюдаемому движению, в отличие от поступательной скорости $\vec{v}$, которую можно непосредственно измерить в каждой точке.
 Вращательное зондирование — увлекательная тема. Но поймите, что истинное общее движение твердого тела описывается векторным полем скорости с вращающейся и параллельно поступательной компонентами. Это называется теоремой Шаля.
Вращательное зондирование — увлекательная тема. Но поймите, что истинное общее движение твердого тела описывается векторным полем скорости с вращающейся и параллельно поступательной компонентами. Это называется теоремой Шаля.[Геометрия] $\vec{\omega}$ является ключом к пониманию лежащей в основе геометрии движения. Под геометрией я подразумеваю ключевые точки и линии в пространстве, которые дают представление о движении. Я говорю здесь о концепции оси вращения .
Итак, как определить $\vec{\omega}$? Каждый из трех вышеприведенных аспектов имеет собственное определение вращательного движения, и каждый говорит об одном и том же.
Используя кинематику, вы должны описать производную вектора, движущегося по вращающейся системе отсчета, чтобы установить общее правило, что $$ \frac{{\rm d} \vec{A} }{{\rm d}t} = \frac{ \partial \vec{A}}{\partial t} + \vec{\omega} \times \vec{A} $$, который используется для определения движения частиц на телах и вывода кинематического уравнения, показанного выше.
 . Это своего рода круговой аргумент, поскольку понятие скорости вращения кадра просто добавлено туда, и, поскольку все это работает, это означает, что наши догадка была верной.
. Это своего рода круговой аргумент, поскольку понятие скорости вращения кадра просто добавлено туда, и, поскольку все это работает, это означает, что наши догадка была верной.Использование векторного поля, описываемого точками, которые движутся, но сохраняют фиксированное расстояние друг от друга, также приводит к определению $\vec{\omega}$. Математика немного сложнее, но расстояние между двумя точками A и B определяется как $\ell_{AB} = \sqrt{ (\vec{r}_A — \vec{r}_B) \cdot ( \vec{r}_A — \vec{r}_B)}$ и дифференцирование по времени с помощью цепного правила дает что-то вроде $$(\vec{r}_A — \vec{r}_B) \cdot ( \vec{ v}_A — \vec{v}_B) = 0$$, которая решается либо вращательным относительным движением, либо чисто поступательным движением. Абсолютное движение — комбинация этих двух и, следовательно, теорема Шаля.
Используя геометрию, вы можете показать, что существует геометрическое место точек в пространстве, описывающее бесконечную прямую.
 На этой линии движение частиц тела происходит только параллельно этой линии. Это определение оси вращения. Эта скорость на оси разлагается как скаляр, кратный вектору вращения $\vec{v}_{axis} = h\, \vec{\omega}$, где $h$ называется шагом и является отношение поступательной скорости к скорости вращения. Движение все частицы на теле описываются положением оси вращения $\vec{r}$, шагом $h$, а также величиной и направлением скорости вращения $\vec{\omega}$ $$ \vec {v} = h\,\vec{\omega} + \vec{r} \times \vec{\omega} $$ Вы можете переключаться между тремя компонентами скорости и геометрическим разложением $\vec{r }$, $h$ и $\vec{\omega}$ свободно.
На этой линии движение частиц тела происходит только параллельно этой линии. Это определение оси вращения. Эта скорость на оси разлагается как скаляр, кратный вектору вращения $\vec{v}_{axis} = h\, \vec{\omega}$, где $h$ называется шагом и является отношение поступательной скорости к скорости вращения. Движение все частицы на теле описываются положением оси вращения $\vec{r}$, шагом $h$, а также величиной и направлением скорости вращения $\vec{\omega}$ $$ \vec {v} = h\,\vec{\omega} + \vec{r} \times \vec{\omega} $$ Вы можете переключаться между тремя компонентами скорости и геометрическим разложением $\vec{r }$, $h$ и $\vec{\omega}$ свободно.
$\endgroup$
3
$\begingroup$
То, что вы называете линейной скоростью, — это просто классическая скорость тестовой массы в м/с. Угловая скорость говорит вам, какой «угол» вы преодолеваете в секунду при движении по кругу (то есть при вращении).
Предположим, вы делаете один полный оборот в секунду. Чем больше радиус вращения, тем быстрее вы должны двигаться, чтобы пройти всю окружность. Вот почему линейная скорость растет с радиусом, если предполагается, что угловая скорость остается постоянной.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Величины вращательной кинематики | безграничная физика |
Угловое положение, тета
Угол поворота — это мера величины (угла), на которую фигура поворачивается вокруг фиксированной точки — часто центра круга.
Цели обучения
Оцените взаимосвязь между радианами и оборотом CD
Ключевые выводы
Ключевые точки
- Длина дуги Δs — это расстояние, пройденное по круговой траектории. r — радиус кривизны кругового пути.
- Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определим угол поворота
Δθ\Delta \thetaΔθ
как отношение длины дуги к радиусу кривизны:
Δθ\Delta \thetaΔθ
= Δs/r.
- За один полный оборот угол поворота равен 2π.
Ключевые термины
- Угловое положение : Угол в радианах (градусах, оборотах), на который точка или линия повернута в определенном направлении вокруг указанной оси.

Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (CD) вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определим угол поворота
Δθ\Delta \thetaΔθ
как отношение длины дуги к радиусу кривизны:
Δθ=Δs/r\Delta \theta = \Delta \text{s}/\text{r}Δθ=Δs/r
(показано на ).
Угол поворота : Все точки на компакт-диске перемещаются по дугам окружности. Все ямки вдоль линии от центра к краю перемещаются на один и тот же угол Δ за время Δt.
В математике угол поворота (или угловое положение) — это мера величины (то есть угла), на которую фигура поворачивается вокруг фиксированной точки (часто центра круга, как показано на рисунке).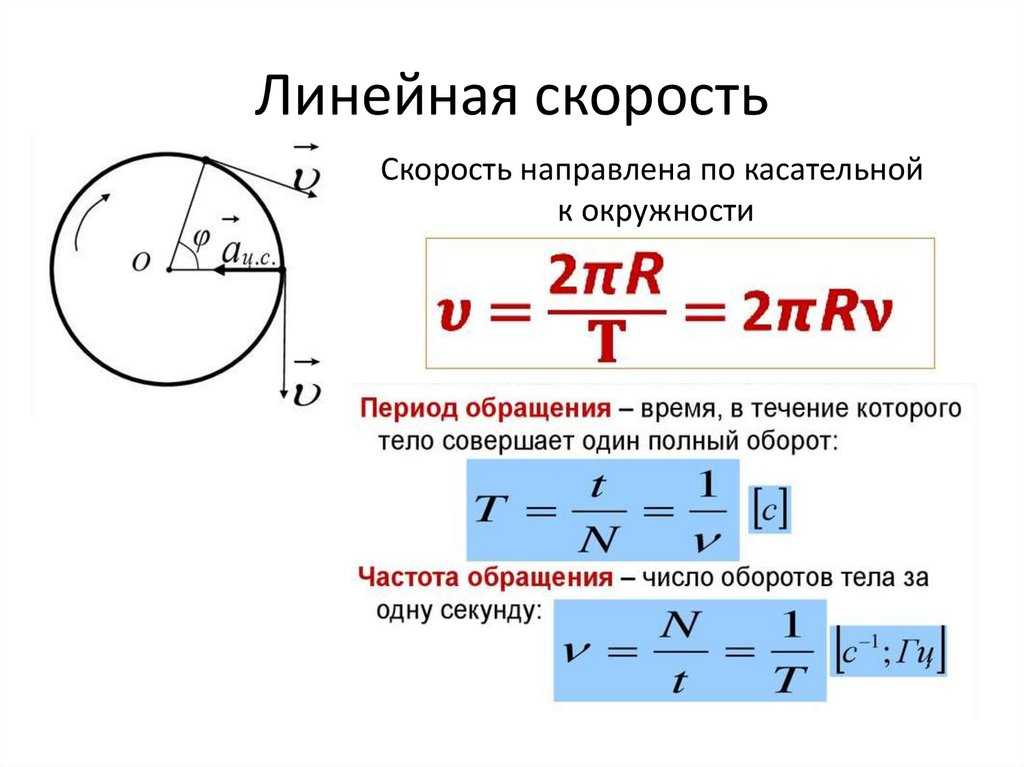
Угол θ и длина дуги s : Радиус окружности поворачивается на угол Δ. Длина дуги Δs описана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории. r — радиус кривизны кругового пути. Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r. Длина окружности равна 2πr. Таким образом, за один полный оборот угол поворота равен:
Δθ=(2πr)/r=2π\Delta \theta = (2 \pi \text{r})/\text{r} = 2 \piΔθ=(2πr )/r=2π
.
Этот результат является основой для определения единиц, используемых для измерения углов поворота, как радианы (рад), определяемые следующим образом:
2π рад = 1 оборот.
Если
Δθ\Delta \thetaΔθ
= 2π рад, то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в окружности или одном обороте 360º, отношение между радианами и градусами, таким образом, равно 2π рад=360º, так что:
1рад = 360º/2π = 57,3º.
Угловая скорость, Омега
Угловая скорость ω — это скорость изменения угла, математически определяемая как ω =
Δθ\Delta \thetaΔθ
/Δt/\Delta \text{t}/Δt
.
Цели обучения
Изучите скорость вращения объекта на основе угловой скорости
Ключевые выводы
Ключевые моменты
- Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость.
- Угловая скорость ω аналогична линейной скорости v.
- Мы можем записать соотношение между линейной скоростью и угловой скоростью двумя разными способами: v=rω или ω=v/r.
Ключевые термины
- угловая скорость : Векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
Чтобы выяснить, насколько быстро вращается объект, мы определяем угловую скорость ω как скорость изменения угла. В символах это
В символах это
ω=Δθ/Δt\omega = \Delta \theta/\Delta \text{t}ω=Δθ/Δt
,
где угловой поворот Δ происходит за время Δt. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость ω аналогична линейной скорости v. Чтобы найти точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается на длину дуги Δs за время Δt, поэтому она имеет линейную скорость v = Δs/Δt.
Из
Δθ=(Δs)/r\Delta \theta = (\Delta \text{s})/\text{r}Δθ=(Δs)/r
мы видим, что
Δs=r⋅ Δθ\Delta \text{s} = \text{r}\cdot \Delta \thetaΔs=r⋅Δθ
. Подставляя это в выражение для v, получаем
v=(r⋅Δθ)/(Δt)=r(Δθ/Δt)=rω\text{v} = (\text{r}\cdot\Delta \theta)/ (\Delta \text{t}) = \text{r}(\Delta \theta/\Delta \text{t}) = \text{r}\omegav=(r⋅Δθ)/(Δt)=r( Δθ/Δt)=rω
.
Мы можем записать это соотношение двумя разными способами: v=rω или ω=v/r.
Первое соотношение утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, поэтому она наибольшая для точки на ободе (наибольшая r), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью. Второе соотношение можно проиллюстрировать, рассмотрев шину движущегося автомобиля, как показано на рисунке ниже. Обратите внимание, что скорость точки в центре шины равна скорости v автомобиля. Чем быстрее движется автомобиль, тем быстрее вращается шина — большое v означает большое ω, потому что v=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет производить большую линейную скорость (v) автомобиля.
Угловая скорость : Автомобиль, движущийся вправо со скоростью v, имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси равна v, такая же, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v=rω, где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Таким образом, автомобиль движется вперед с линейной скоростью v=rω, где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Угловое ускорение, Alpha
Угловое ускорение — это скорость изменения угловой скорости, математически выраженная как
α=Δω/Δt\alpha = \Delta \omega/\Delta \text{t}α=Δω/Δt
.
Цели обучения
Объясните взаимосвязь между угловым ускорением и угловой скоростью
Ключевые выводы
Ключевые моменты
- Чем быстрее происходит изменение угловой скорости, тем больше угловое ускорение.
- При круговом движении линейное ускорение касается окружности в интересующей точке и называется тангенциальным ускорением.
- При движении по окружности центростремительное ускорение относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение.

Ключевые термины
- угловое ускорение : скорость изменения угловой скорости, часто обозначаемая α.
- тангенциальное ускорение : Ускорение в направлении касательной к окружности в интересующей точке при круговом движении.
Угловое ускорение – это скорость изменения угловой скорости. В единицах СИ он измеряется в радианах на секунду в квадрате (рад/с 2 ) и обычно обозначается греческой буквой альфа (
α\alphaα
).
Рассмотрим следующие ситуации, в которых угловая скорость непостоянна: когда фигурист тянет руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается при выключении. Во всех этих случаях имеет место угловое ускорение, при котором
ω\omegaω
изменений. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:
Угловое ускорение определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:
α=Δω/Δt\alpha = \Delta \omega/\Delta \text{t}α=Δω/Δt
, где
Δω\Delta \omegaΔω
— изменение угловой скорости, а
Δt\Delta \text{t}Δt
— изменение во времени. Единицы углового ускорения (рад/с)/с или рад/с 2 . Если
ω\omegaω
увеличивается, то
α\alphaα
положительно. Если
ω\omegaω
убывает, то
α\alphaα
отрицательно.
Полезно знать, как связаны линейное и угловое ускорения. При круговом движении есть ускорение, которое составляет по касательной к окружности в интересующей точке (как показано на диаграмме ниже). Это ускорение называется тангенциальным ускорением, а т .
Тангенциальное ускорение : При круговом движении ускорение может возникать по мере изменения величины скорости: a касается движения. Это ускорение называется тангенциальным ускорением.
Тангенциальное ускорение относится к изменению величины скорости, но не ее направления. При круговом движении центростремительное ускорение a c относится к изменениям направления скорости, но не к ее величине. Объект, совершающий круговое движение, испытывает центростремительное ускорение (как показано на диаграмме ниже). Таким образом, t и c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t непосредственно связано с угловым ускорением и связано с увеличением или уменьшением скорости (но не ее направления).
Центростремительное ускорение : Центростремительное ускорение возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Лицензии и атрибуции
Контент под лицензией CC, совместно используемый ранее
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, Конкретное указание авторства
- Угол поворота. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Угловое положение. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики.
 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики.
 10 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
10 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Угловое ускорение. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Angular_acceleration. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- угловое ускорение. Предоставлено : Викисловарь.

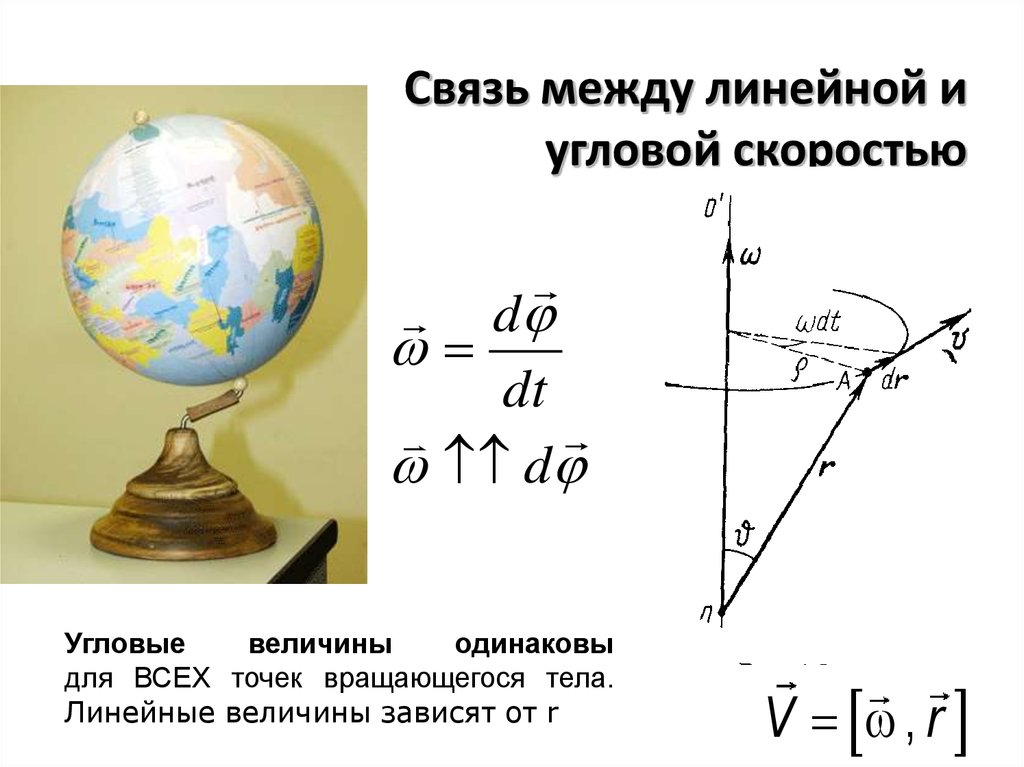 Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
 Специальных единиц измерения импульса нет. Размерность импульса — это просто произ- ведение размерности массы на размерность скорости: [p] = [m] · [v] = кг · м /с .
Специальных единиц измерения импульса нет. Размерность импульса — это просто произ- ведение размерности массы на размерность скорости: [p] = [m] · [v] = кг · м /с . Единицей работы в СИ служит джоуль (Дж).
Единицей работы в СИ служит джоуль (Дж).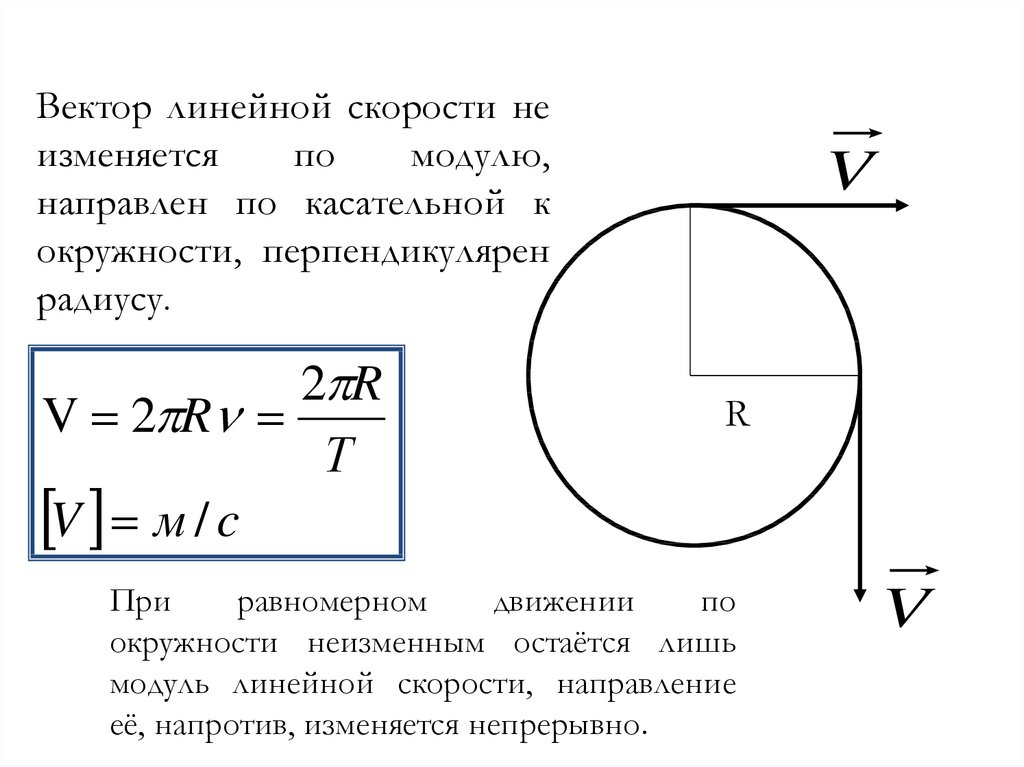
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.004 с.)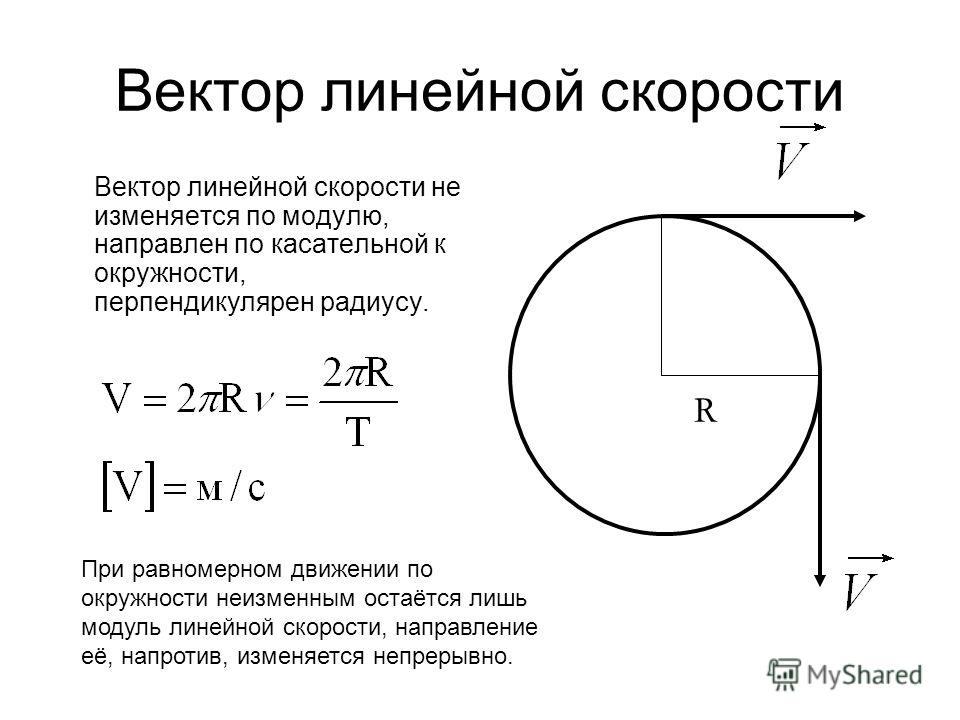 Вращательное зондирование — увлекательная тема. Но поймите, что истинное общее движение твердого тела описывается векторным полем скорости с вращающейся и параллельно поступательной компонентами. Это называется теоремой Шаля.
Вращательное зондирование — увлекательная тема. Но поймите, что истинное общее движение твердого тела описывается векторным полем скорости с вращающейся и параллельно поступательной компонентами. Это называется теоремой Шаля. . Это своего рода круговой аргумент, поскольку понятие скорости вращения кадра просто добавлено туда, и, поскольку все это работает, это означает, что наши догадка была верной.
. Это своего рода круговой аргумент, поскольку понятие скорости вращения кадра просто добавлено туда, и, поскольку все это работает, это означает, что наши догадка была верной.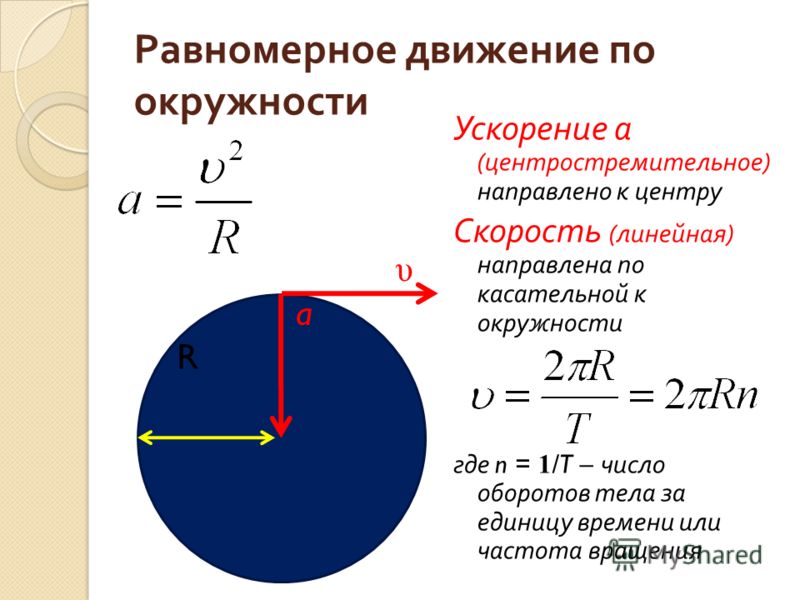 На этой линии движение частиц тела происходит только параллельно этой линии. Это определение оси вращения. Эта скорость на оси разлагается как скаляр, кратный вектору вращения $\vec{v}_{axis} = h\, \vec{\omega}$, где $h$ называется шагом и является отношение поступательной скорости к скорости вращения. Движение все частицы на теле описываются положением оси вращения $\vec{r}$, шагом $h$, а также величиной и направлением скорости вращения $\vec{\omega}$ $$ \vec {v} = h\,\vec{\omega} + \vec{r} \times \vec{\omega} $$ Вы можете переключаться между тремя компонентами скорости и геометрическим разложением $\vec{r }$, $h$ и $\vec{\omega}$ свободно.
На этой линии движение частиц тела происходит только параллельно этой линии. Это определение оси вращения. Эта скорость на оси разлагается как скаляр, кратный вектору вращения $\vec{v}_{axis} = h\, \vec{\omega}$, где $h$ называется шагом и является отношение поступательной скорости к скорости вращения. Движение все частицы на теле описываются положением оси вращения $\vec{r}$, шагом $h$, а также величиной и направлением скорости вращения $\vec{\omega}$ $$ \vec {v} = h\,\vec{\omega} + \vec{r} \times \vec{\omega} $$ Вы можете переключаться между тремя компонентами скорости и геометрическим разложением $\vec{r }$, $h$ и $\vec{\omega}$ свободно.

 10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
10 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution  10 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
10 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция 