5 фактов, которые вы должны знать

Периодическое движение объекта, частицы или количества через равные промежутки времени относительно среднего положения известно как колебание. 

Когда тело колеблется, оно включает как линейное, так и угловое смещение, это угловое смещение известно как угловая частота колебаний. В физике есть также другие термины для угловой частоты, такие как угловая скорость и орбитальная частота. 

Угловая частота — это скалярная мера углового смещения колеблющейся частицы. Для синусоидальных волн это называется скоростью изменения фазы. Когда мяч, привязанный к веревке, вращается по кругу, скорость, с которой он совершает одно колебание на 360 градусов, называется угловой частотой. 

Изображение Фото: Пользователь: Stannered, Угловая скорость, CC BY-SA 3.0

Формула угловой частоты колебаний

Изменение угла, которое происходит за одну секунду, называется угловой частотой. Следовательно, основная формула для определения угловой частоты:

[латекс]\omega =\frac{\Theta}{t}[/латекс]

Здесь;

ω — угловая частота

Θ — угол, на который перемещается объект. {2}=\frac{g}{L}[/латекс]

[латекс]\omega=\sqrt{\frac{g}{L}}[/латекс]

Здесь;

g — ускорение свободного падения, а L — длина маятника.

Угловая частота колебаний объекта

Для колеблющегося объекта уравнение SHM имеет вид:

[латекс]х=Асин(\омега т+\фи)[/латекс]

Здесь;

x — смещение объекта 

A — амплитуда колебаний 

𝛟 — фазовый переход

ω — угловая частота 

Для колеблющегося объекта угловая частота задается как; 

ω = 2πf

Он говорит о том, на какой угол поворачивается объект для смещения. 

Как найти угловую частоту колебаний 

Для разных объектов и сценариев используется другая формула для вычисления угловой частоты колебаний. 

[латекс]х=Асин(\омега т+\фи)[/латекс]

Например, амплитуда колебаний составляет 0.14 м; изменение фазы равно 0. Теперь, чтобы покрыть 14 см за 8.5 секунд, угловая частота рассчитывается по формуле;

[латекс]0.14=0.14sin(8.5\омега)[/латекс]

[латекс]1=грех(8. {-1}[/латекс]

Часто задаваемые вопросы (FAQ)

Какая угловая частота колебаний?

Повторяющееся движение частицы относительно фиксированной точки называется колебанием. 

Изменение угла частицы — это угловая частота колебаний. В физике это также называется скоростью изменения фазы. Это скалярный элемент, поскольку это просто угловое смещение без направления. Формула для угловой частоты имеет вид;

ω = 2πf

Как угловая частота связана с периодом времени?

Колеблющиеся объекты включают как линейные, так и угловые перемещения. 

Основная формула для угловой частоты представлена ​​как;

[латекс]\omega=\frac{\Theta}{t}[/латекс]

Он показывает соотношение времени и угловой частоты колебаний. 

Теперь общая формула для угловой частоты:

ω = 2πf

Подставляя данное соотношение

[латекс]f=\frac{1}{T}[/latex]

Мы получаем;

[латекс]\omega=\frac{2\Pi }{T}[/латекс]

Это уравнение связывает угловую частоту и период времени. {-1}[/латекс]

Когда объект проходит один полный цикл за одну секунду, угловая частота становится равной 1. 

Угловая частота совпадает с частотой?

Число колебаний, совершаемых объектом за одну секунду, называется частотой. 

Нет, частота и угловая частота — это не одно и то же. Угловая частота — это изменение угла колеблющейся частицы за единицу времени, тогда как частота — это колебание, совершаемое за одну секунду. Оба они представляют собой разные термины, используемые для разных концепций физики. 

Физики разогнали «спиннеры» до миллиарда оборотов в секунду

Две команды физиков независимо разогнали с помощью лазеров нанометровые «спиннеры» до скорости порядка одного миллиарда оборотов в секунду — самой высокой скорости вращения, полученной в лаборатории. Первая группа из Швейцарской высшей технической школы Цюриха (ETH Zurich) заставляла вращаться наночастицу кремнезема, а вторая группа, состоящая из китайских и американских исследователей, использовала в качестве «спиннера» наногантелю. Работа ученых поможет лучше понять такие тонкие эффекты, как вращение Казимира, связанное с квантовыми флуктуациями вакуума. Статьи опубликованы в Physical Review Letters [1, 2], кратко о них сообщает Physics, препринты работ выложены на сайте arXiv.org [1, 2].

Скорость вращения любого объекта ограничена пределом его прочности. Чем быстрее вращается объект, тем большую скорость развивают его частицы и тем большая сила нужна, чтобы заставлять их повернуть и удерживать тело в целости. Другими словами, при увеличении скорости растет центробежная сила, которая стремится «разорвать» тело. Впрочем, называть центробежную силу «силой» не совсем правильно, поскольку она возникает только в неинерциальной системе отсчета (подробнее о ее природе можно прочитать в этой заметке).

Заметнее всего действие этой «фиктивной силы» проявляется в точках, наиболее удаленных от центра вращения объекта: F = mω²r, где m — масса точки, r — ее расстояние до центра, а ω — угловая скорость. Из-за этого частота вращения макроскопических объектов редко превышает тысячу оборотов в секунду. Например, частота вала газогенератора двигателя PW207K вертолета «Ансат» может достигать 60000 оборотов в минуту (1000 оборотов в секунду), а турбина двигателя CFM56, который устанавливается на самолетах фирм Boeing и Airbus, вращается с частотой около 5200 оборотов в минуту (менее 90 оборотов в секунду).

Уменьшая размеры объекта, можно заставить его вращаться гораздо быстрее. Оказывается, что для достижения сверхвысоких скоростей удобнее всего использовать частицы размером порядка ста нанометров, подвешенные в воздухе с помощью лазерного излучения (так называемая оптическая ловушка). Направляя на связанную частицу свет с круговой поляризацией, можно передать ей угловой момент и увеличить ее угловую скорость (эффект Садовского). Таким образом можно избежать механического трения, которое поглощает энергию и мешает разгонять частицу, а также контролировать центр вращения с точностью, сравнимой с теоретическим пределом.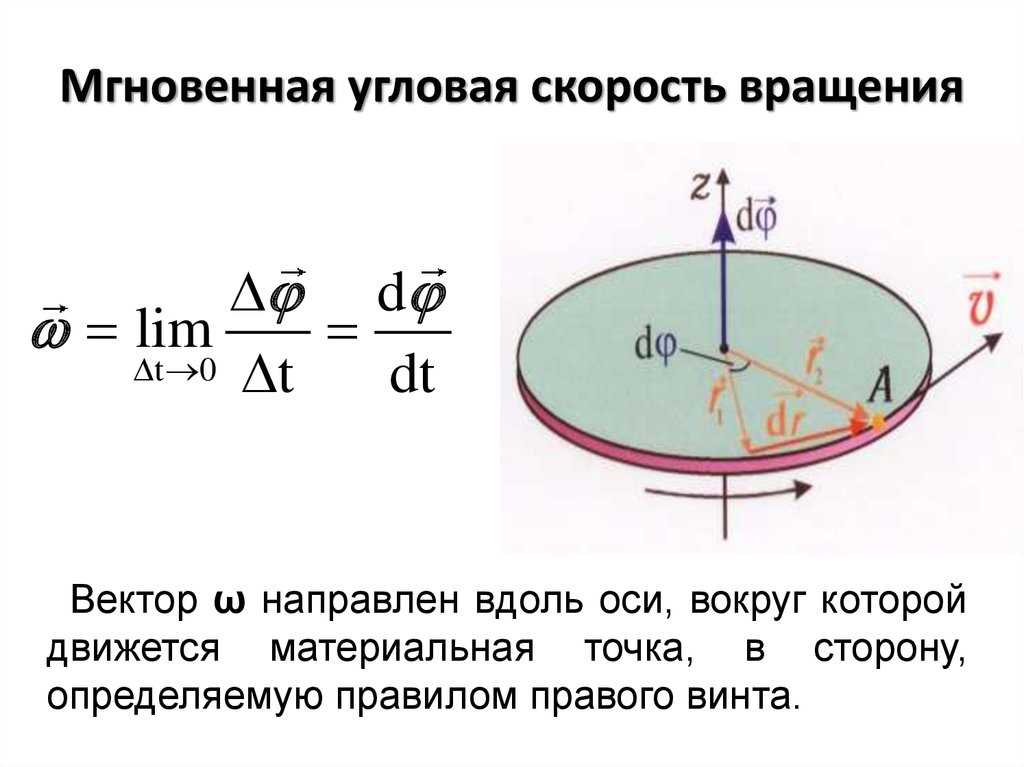

К сожалению, на высоких скоростях начинает сказываться трение наночастицы о воздух, которое также уносит энергию частицы. Бороться с этим трением можно только откачивая установку до сверхнизких давлений, создавая в ней вакуум. Из-за подобных технических сложностей ученым не удавалось достичь в лаборатории скоростей вращения, превышающих по порядку десяти мегагерц. В новых работах ученым удалось преодолеть это препятствие, подтвердить теоретические предсказания и достичь частоты вращения порядка одного гигагерца.

Первая группа исследователей под руководством Лукаса Новотного (Lukas Novotny), использовала в качестве «спиннера» частицу кремнезема (проще говоря, обычного стекла) приближенно сферической формы и диаметром около ста нанометров. Для уменьшения потерь физики откачали установку до давления порядка 10⁻⁸ атмосфер и увеличили длину волны лазера, который использовался для разгона частицы, до 1565 нанометров. Это позволило уменьшить скорость нагрева частицы — в предыдущих экспериментах такой нагрев заставлял частицу «выскакивать» из ловушки и мешал разогнать ее выше определенного предела.

В результате ученые обнаружили, что с уменьшением давления при фиксированной мощности лазера и увеличении мощности при фиксированном давлении угловая скорость вращения частицы линейно растет, причем экспериментальная зависимость хорошо согласуется с теорией. Максимальная частота, полученная в этом эксперименте, достигала 1,03 гигагерц, что отвечало скорость краев частицы порядка 300 метров в секунду, центробежному ускорению порядка 10¹² метров на секунду в квадрате и напряжению порядка 0,2 гигапаскаль. Для сравнения, критическое напряжение, при котором частица кремнезема разрывается, составляет примерно 10 гигапаскаль.

Вторая группа, под руководством Тунцана Ли (Tongcang Li), заставляла вращаться наногантели — связанные друг с другом частицы кремнезема. Чтобы изготовить такие гантели, ученые «растворяли» наночастицы кремнезема в воде и получали коллоидную суспензию, а затем с помощью ультразвукового небулайзера заставляли воду формировать микрометровые капли, взвешенные в воздухе. В некоторых из капель находилось две сферические частицы кремнезема; после испарения воды частицы оставались связаны в наногантели, которые ученые использовали в дальнейших опытах. Отношение диаметра шаров к расстоянию между ними для всех полученных наногантелей было примерно равно двум.

Так же как и группа швейцарских ученых, группа под руководством Тунцана Ли помещала наногантели в оптическую ловушку, откачивала установку до давления порядка 10⁻⁷ атмосфер и светила на частицы лазером с круговой поляризацией и длиной волны около 1550 нанометров. Аналогично швейцарцам, физики получили, что скорость вращения линейно растет при уменьшении давления, а предельная частота вращения в этом случае составила примерно 1,1 гигагерц — при бо́льших скоростях гантель разрывалась под действием центробежной силы.

Тем не менее, конструкция установки, аналогичная опыту Кавендиша, в котором проволока крутильных весов заменена на лазерное излучение, позволяет провести на ней качественно другие эксперименты. Если заменить в ней свет с круговой поляризацией на линейно поляризованный свет, наногантели будут колебаться, а не крутиться, что позволит в будущем измерить вращательный эффект Казимира (Casimir torque) и исследовать природу квантовой гравитации.

Впрочем, ученые признаются, что изначально они не ставили перед собой практических целей. Например, соавтор первой работы, Рене Рейманн (René Reimann), говорит: «Если честно, это просто было очень круто — иметь механический объект с самой высокой скоростью вращения в мире прямо перед нами». Тем не менее, работа ученых может пригодиться при изучении межзвездной пыли и вакуумного трения, исследовании поведения материалов и взаимосвязи между вращательными и поступательными степенями свободы в экстремальных условиях.

В ноябре прошлого года американские исследователи-нанотехнологи изготовили с помощью фотолитографии самый маленький в мире фиджет-спиннер, размер которого составил примерно сто микрометров.

Дмитрий Трунин

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Объяснение угловой частоты — Unacademy

Вы узнали о частотной скорости объекта и его различных движениях. У нас есть представление о частоте. Всякий раз, когда объект вращается вокруг своей оси, он образует угол. Например, возьмите веревку и привяжите к одному ее концу резиновый шарик, чтобы шарик качался по кругу вокруг своей оси. (просто представьте, что нити не существует, а шарик вращается по окружности, образуя угол вокруг своей воображаемой оси) Вы заметите, что он движется с определенной скоростью, совершая 360°. Это та ситуация, когда нам нужна угловая частота для вычисления. Давайте проведем подробный анализ угловой частоты.

Что такое Угловая частота ?

Прежде чем понять угловую частоту, давайте рассмотрим значение периода времени и углового смещения.

Период времени — это время, за которое объект совершает одно колебание.

Угловое смещение — кратчайший угол, совершаемый объектом из первого положения во второе положение остановки при вращении по окружности.

Определение угловой частоты – это угловое смещение элемента волны в единицу времени, или, другими словами, можно сказать, что это скорость, с которой происходит изменение вращения, или скорость, с которой изменяется возникают синусоидальные волны. Например, если вы скажете, что объект имеет высокую угловую частоту, он будет вращаться очень быстро. Угловая частота — это величина угловой скорости. Таким образом, это скалярная величина, т. е. не имеющая направления. Угловая частота помогает найти скорость вращения тела в периодическом движении.

Различные названия. Угловая скорость, радиальная частота, круговая частота, орбитальная частота, частота в радианах и пульсация.

Вывод формулы

Представьте, что каучук, прикрепленный к струне, делает полный круг, т. е. 2π за время T. Мы знаем, что угловая частота — это радиан угла, на который тело движется в единицу времени.

Таким образом, мы можем записать угловую частоту как

ω =2π/T, где ω — угловая частота.

Также мы знаем, что частота равна 1/T. Таким образом, угловая частота через частоту (f) может быть записана как

ω =2πf

Единица

Единица СИ угловой частоты в радианах в секунду.

Примеры Угловая частота

1. Круговое движение

Для орбитального объекта существует связь между расстоянием от оси «r», тангенциальной скоростью вращения «v» и угловой скоростью вращения «v». Вращающееся тело проходит расстояние «vT» за период времени «T». Расстояние, пройденное телом, равно длине окружности, которая, как мы знаем, равна 2πr. Таким образом, мы получаем,

ω= v/r.

2. Электроснабжение.

На электростанции генераторы вращаются с определенной скоростью. Эта скорость вращения называется угловой частотой, которая определяет частоту, с которой производится электричество. Если необходимо замедлить подачу электроэнергии, необходимо уменьшить угловую частоту генераторов.

3. Спутники

Если спутник хочет избежать земного притяжения, то сила, действующая на спутник, должна быть равна силе земного притяжения, т. е.

GMm /r2 =mω2r, где M — масса большего тела, а G — гравитационная постоянная.

Чтобы сделать круг, угловая частота должна быть равна,

ω окружность=√GM/√r2

Решенные примеры

1. Рассчитать угловую частоту объекта, вращающегося с периодом времени 1 мин.

Решение:

 Дано- T= 1 мин= 60 с

Формула- ω =2π/T

Применяя формулу, ω=2*180/60 = 360/60= 60 рад/с или 600/с

Следовательно, угловая частота равна 600/сек.

2. Рассчитайте время, необходимое объекту для завершения вращения, если угловая частота равна 900/сек.

Решение:

Дано: ω=900/сек

Формула – T =2π/ ω

Таким образом, применяя формулу, получаем

T= 2*180/90= 3600/900= 40сек.

Таким образом, время, необходимое объекту для завершения вращения, составляет 40 секунд.

Заключение

Таким образом, мы можем заключить, что угловая частота существует, когда объект движется по круговой траектории или если он колеблется. Угловая частота — это скорость изменения углового смещения, поэтому ее единицей измерения являются радианы в секунду. Его единица зависит от решаемой задачи. Предположим, проблема связана с каруселью. В таком случае угловую частоту будем брать в радианах в секунду, а если речь идет о вращении Луны вокруг Земли, то угловая частота будет в радианах в сутки. Полезно сообщить период времени вращающегося объекта.

Угловая скорость: формула, единица измерения и расчет

Представьте на мгновение, что вы лежите на кровати и смотрите вверх на потолочный вентилятор (или просто посмотрите на вентилятор на изображении ниже). Для большинства вентиляторов, если потянуть за цепь, скорость вентилятора изменится. Как бы вы описали эту скорость? Думаете ли вы об этом в милях в час, как вы можете думать о скорости автомобиля? Вероятно, нет, так как вентилятор не движется по потолку.

Скорее всего, вы думаете о скорости вентилятора с точки зрения того, сколько полных круговых оборотов он делает за те несколько секунд, что вы на него смотрите. Когда вы увеличиваете скорость вентилятора, он делает гораздо больше оборотов за то же время. Эта концепция скорости — движение по кругу, а не по прямой — называется угловой скоростью.

Рис. 1 — Потолочный вентилятор, используемый для демонстрации угловой скорости.

Угловая скорость и частота

Как следует из названия, угловая скорость связана с тем, насколько быстро изменяется угол, поскольку углы раскрываются в форме круга.

Угловая скорость — это скорость вращения объекта на центральный угол во времени.

Угловая скорость часто также называется угловой скоростью , хотя между ними есть небольшая, но важная разница. См. Раздел ниже под названием «Разница между угловой скоростью и скоростью» для дальнейшего объяснения.

В общем, частота определяется как то, как часто что-то происходит в течение определенного периода времени, обычно одной секунды в физике. Это будет измеряться в циклах в секунду или Герцах (Гц). Говоря о круговом движении, частота относится к числу оборотов или оборотов в секунду. Это немного отличается от определения угловой частоты.

Угловая частота — это градус вращения объекта в радианах за одну секунду.

Это означает, что угловая частота связана с частотой масштабным коэффициентом \(2\pi\), поскольку один оборот равен \(2\pi\) радианам.

Функционально определение угловой скорости и угловой частоты представляет собой одно и то же и, следовательно, будет иметь одну и ту же формулу (показана ниже в следующем разделе).

Дополнительные сведения о круговом движении см. в нашей статье «Круговое движение и гравитация».

Формула угловой скорости

Любая скорость или скорость измеряется отношением величины смещения объекта к количеству времени, которое требуется для перемещения. Для линейной скорости или скорости это обычно находится путем деления расстояния на время. Но с угловой скоростью вас больше волнует не то, НАСКОЛЬКО ДАЛЬШЕ перемещается объект, а то, какой оборот он совершает.

Формула для нахождения угловой скорости или скорости \(\omega\) представляет собой отношение углового смещения \(\Theta\) ко времени \(t\) в секундах: \[\omega=\frac{ \Theta}{t}.\]

Угловая мера измеряется в радианах (не в градусах). Итак, полезно вспомнить, что один полный оборот (равный 360 градусам) равен \(2\pi\) радианам.

Рис. 2 — Окружность, вращающаяся на угол \(\Theta\) радиан.

Единица измерения угловой скорости

Поскольку все скорости определяются отношением смещения объекта во времени, единицей измерения скорости всегда является

\[\text{скорость}=\frac{\text{единица смещения}}{\text{единица времени}}.\]

Таким образом, для угловой скорости или скорости единицы будут радиан в секунду или рад/сек .

Разница между угловой скоростью и скоростью

Разница между угловой скоростью и угловой скоростью такая же, как разница между линейной скоростью и линейной скоростью. Для обоих скорость не считается вектором . Это просто величина, не связанная с направлением. Но скорость — это вектор. Он имеет как величину, так и направление.

Для кругового движения, нужное вам направление по часовой стрелке и против часовой стрелки. Если это считается направлением, это также означает, что все может двигаться в отрицательном направлении. Для угловой скорости отрицательного значения нет. Он просто показывает, насколько быстро объект вращается по кругу в любом направлении. Но угловая скорость положительна, если объект движется вдоль оси вращения. Направление, противоположное оси вращения, будет отрицательным.

Часто ось вращения определяется правилом правой руки . См. нашу статью «Крутящий момент и угловое ускорение», чтобы узнать больше о правиле правой руки.

Разница между угловой скоростью и линейной скоростью

Вспомните первоначальный пример потолочного вентилятора как ваше понятие угловой скорости. Посмотрите на одну лопасть вентилятора. Имеет ли все лезвие одинаковую угловую скорость? Или конец лезвия быстрее или медленнее, чем кронштейн, удерживающий лезвие на двигателе? Все лезвие совершает один и тот же угловой оборот каждую секунду, потому что все лезвие совершает каждый оборот как единое целое. Итак, угловая скорость одинакова по всей длине лопасти вентилятора.

Но каждый конец лопасти вентилятора не проходит одно и то же расстояние за каждый оборот. Кронштейн, который соединяет лопасть вентилятора с двигателем, образует довольно маленький круг, который будет иметь небольшую окружность или расстояние. Конец лопасти вентилятора образует довольно большой круг. Его окружность будет больше, и поэтому конец лопасти вентилятора пройдет большее расстояние за то же время. Таким образом, конец лопасти вентилятора имеет более высокую линейную скорость, чем кронштейн, несмотря на ту же угловую скорость. Напомним, что линейная скорость определяется как

\[\text{скорость}=\frac{\text{расстояние}}{\text{время}}. \]

Но существует связь между угловой скоростью и линейной скоростью. Представьте, что вы едете на велосипеде. Чтобы двигаться с более высокой линейной скоростью, вы должны крутить педали быстрее, что также увеличивает вашу угловую скорость. Основным фактором, определяющим линейную скорость вращающегося объекта, является размер окружности, которую он описывает.

Формула для нахождения линейной скорости \(v\) объекта, вращающегося по окружности с радиусом \(r\) и угловой скоростью \(\omega\) равна

\[v=r\omega.\]

Давайте рассмотрим пример использования этой формулы и предыдущей формулы для угловой скорости.

Вы едете на велосипеде с колесами радиусом \(33\, \text{см}\). Ваши колеса совершают \(50\) полных оборотов за 7 секунд. Найдите угловую скорость колес и линейную скорость вашего велосипеда.

Решение

Во-первых, нам нужно сделать пару преобразований, чтобы использовать формулы. Во-первых, угловое смещение предполагается измерять в радианах, а не в оборотах.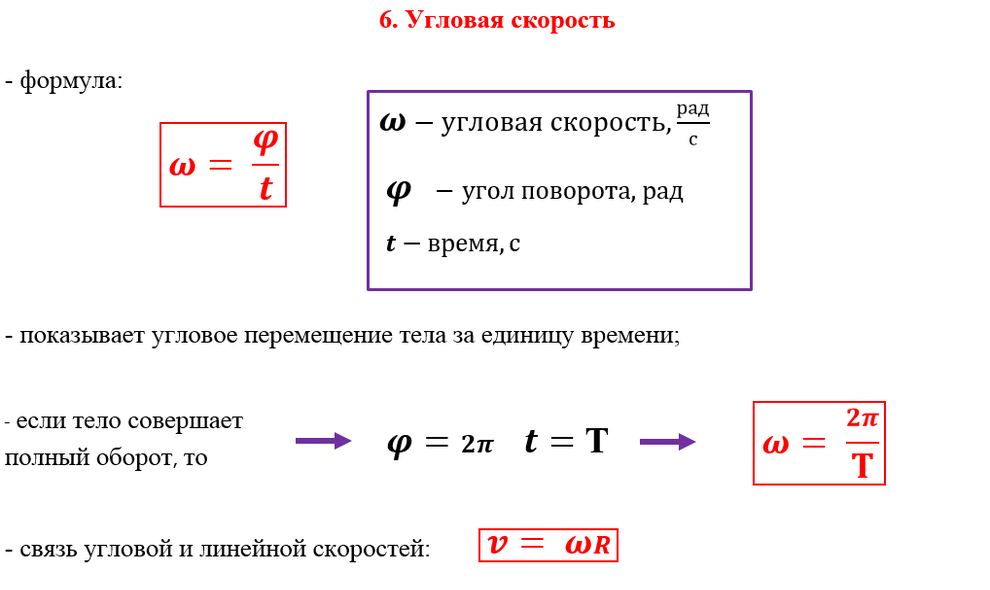 Велосипед делает \(50\) оборотов, и на один оборот приходится \(2\pi\) радиан. Итак, в целом велосипед имеет угловое смещение

\[50(2\pi)=100\pi \, \text{радианы}.\]

Далее, обычно скорость измеряется в метрах в секунду, по крайней мере, в большинстве физических задач. Итак, это единица измерения, которую вы будете использовать здесь. Это означает, что радиус колес велосипеда нужно перевести из сантиметров в метры. Радиус каждого колеса равен \(33\, \text{см}\), что составляет \(0,33\) метра.

Теперь о скорости. Имеет смысл начать с угловой скорости, так как это значение понадобится вам в формуле для линейной скорости. Напомним, что формула угловой скорости равна

\[\omega=\frac{\Theta}{t}.\]

Вы знаете, что \(\Theta=100\pi\) радиан и \(t=7\) секунд. Итак, угловая скорость велосипеда равна

\[\begin{align}\omega &=\frac{100\pi \text{ рад}}{7 \text{ сек}}\\ &\приблизительно44,88 \ ,\text{rad/sec}.\end{align}\]

Затем вам нужно использовать эту скорость, чтобы найти линейную скорость.