Содержание
03 угловая скорость
ЛАБОРАТОРНАЯ
РАБОТА №3
ИЗМЕРЕНИЯ
УГЛОВОЙ СКОРОСТИ
Цель
работы: ознакомиться
со способами измерения угловой скорости,
измерить угловую скорость вращения
электромотора в зависимости от
приложенного напряжения.
МЕТОДИКА ЭКСПЕРИМЕНТА
В
данной работе необходимо измерить
разными способами угловую скорость
диска, жестко закрепленного на валу
электромотора постоянного тока, в
зависимости от приложенного к мотору
напряжения.
Приборы
и устройства, предназначенные для
измерения частоты вращения, называются
тахометрами (от греческого “тахеос”
— быстрый). Следует подчеркнуть, что
тахометры измеряют именно частоту
вращения, а не угловую скорость. Частота
вращения численно равна числу оборотов,
совершаемых в единицу времени. В технике
частоту вращения принято измерять в
единицах “оборот в минуту”. Если
обозначить эту величину буквой
n, то связь
между
и n
выражается соотношением
(1)
Простейший
из тахометров, применяемый для быстрых
оценочных измерений — механический
тахометр (рис. 1). На валу тахометра,
1). На валу тахометра,
которому при контакте передается
вращение исследуемого объекта, установлена
муфта с прикрепленными к ней на шарнирах
грузами. При вращении вала грузы
расходятся и перемещают муфту вдоль
вала. Положение муфты на валу определяется
скоростью вращения. Муфта связана
рычажками со стрелкой, движущейся по
циферблату. Шкала прибора проградуирована
в единицах об/мин.
Очевидным недостатком такого тахометра
является необходимость контакта вала
тахометра с исследуемым вращающимся
объектом, в результате чего изменяется
скорость вращения самого объекта.
Предпочтительнее поэтому пользоваться
бесконтактными методами.
Существует
несколько методов, с помощью которых
частота вращения может быть определена
со значительно большей точностью. Одним
из них является стробоскопический
метод, в котором используется так
называемый стробоскопический эффект.
Различают
два стробоскопических (стробос
— вихрь,
скопео —
смотрю)
эффекта. Первый из них состоит в том,
Первый из них состоит в том,
что быстрая смена отдельных фаз движения
тела воспринимается глазом как непрерывное
движение. Это связано с тем, что клетки
сетчатой оболочки глаза сохраняют
зрительный образ в течение примерно
0,1с.
после исчезновения зримого объекта. И,
если время между появлениями отдельных
изображений меньше 0,1с,
образы сливаются, и возникает иллюзия
непрерывности движения. На этом эффекте
основаны кинематограф и телевидение.
Второй
стробоскопический эффект состоит в
том, что при определенных условиях
возникает иллюзия не движения, а,
наоборот, покоя предмета, который на
самом деле движется.
Если
какой-нибудь объект совершает периодическое
движение (колеблется или вращается), то
при освещении его прерывистыми световыми
вспышками, следующими через равные
промежутки времени, предмет будет
казаться неподвижным, если частота
вспышек в точности равна частоте
колебаний вращения. Объясняется это
тем, что глаз будет отмечать положение
тела в момент световой вспышки и сохранят
этот зрительный образ до следующей
вспышки, которая при равных частотах
вспышек и вращения застанет предмет на
том же месте. Когда частота вспышек в
Когда частота вспышек в
целое число раз больше частоты вращения
картина тоже будет неподвижной, но
теперь будет видно несколько “экземпляров”
предмета. Если отношение частоты вспышек
к частоте оборотов равно k,
то за каждый оборот будет происходить
k
вспышек, которые застанут предмет в
разных положениях, отличающихся на угол
2/k.
Равенство всех углов означает, что тело
вращается с постоянной угловой скорость.
Если частота
вспышек не в точности равна или не в
точности кратна частоте вращения тела,
то оно будет казаться медленно вращающимся
в ту, или другую сторону в зависимости
от соотношения частот. Если частота
вспышек намного больше частоты вращения
или ей величины, каждая последующая
вспышка будет освещать предмет в
положении, когда он еще не сделал полного
оборота, и он будет казаться вращающимся
в сторону, противоположному реальному
вращению тела. Наоборот, если частота
вспышек несколько меньше частоты
вращения тела, кажущееся движение будет
совпадать с направлением истинным.
Такие стробоскопические иллюзии иногда
наблюдаются в кино, когда, например,
частота следования кинокадров больше
или меньше частоты вращения колес.
Стробоскопический
метод измерения частоты вращения
обладает одним существенным недостатком,
заключающийся в том, что одну и ту
неподвижную картину можно наблюдать
при различных значениях k.
Напомним, что k есть
отношение числа вспышек к числу оборотов
предмета. Эта величина может быть как
больше, так и меньше единицы. Если число
вспышек больше числа оборотов, то k>1.
Наоборот, если число вспышек меньше
числа оборотов, то k<1.
Пусть наблюдается
один “экземпляр” предмета. Это возможно,
если за время, равное периоду следования
вспышек, предмет повернулся на угол 2,
4, 6
и т.д. (в общем случае этот угол равен
2m,
где m=1,2,3,)
т.е. совершил 1,2,3,
оборотов (в общем случае m
оборотов). Другими словами, это возможно
при k=1,1/2,1/3,
(в общем случае k=1/m).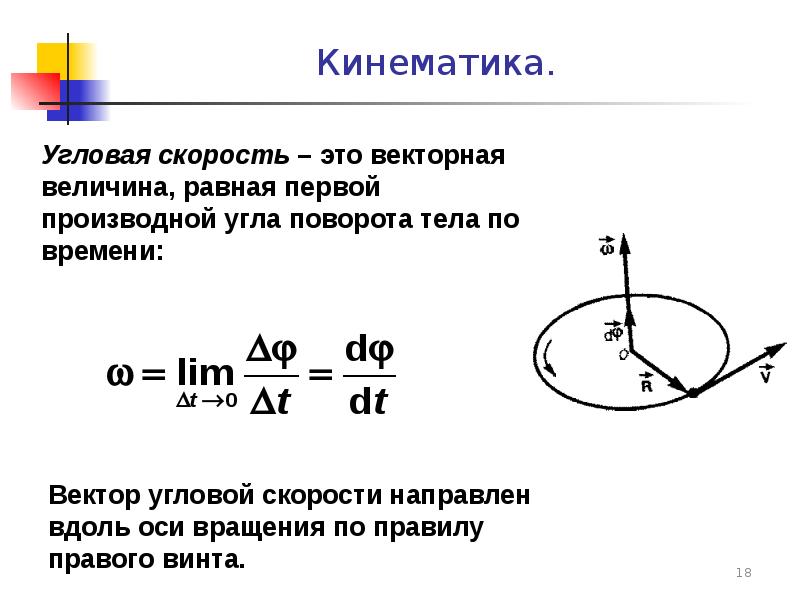
Итак, если при освещении вращающегося
объекта импульсным осветителем
наблюдается один “экземпляр” предмета,
то вывод, который из этого можно сделать
заключается лишь в том, что число оборот
или равно числу вспышек или в целое
число раз меньше числа вспышек.
Такая же
неоднозначность при наблюдении двух
“экземпляров” предмета. Аналогично
можно показать, что такая ситуация
возможна, если k=2,2/3,2/5
и т.д. Нетрудно показать, что неоднозначность
определения числа оборотов стробоскопическим
методом существует при наблюдении любой
неподвижной картинки.
Такого недостатка
лишен другой метод бесконтактного
измерения частоты вращения, идея которого
заключается в следующем. На вращающийся
предмет перпендикулярно оси вращения
жестко укрепляется диск с отверстиями,
равномерно расположенными по его краю.
При своем движении эти отверстия
периодически перекрывают световой
пучок, направленный на фотодатчик. Тем
самым фотодатчик генерирует
последовательность импульсов, частота
которых определяется частотой вращения
и числом отверстий. Количество импульсов
Количество импульсов
в единицу времени подсчитывается
специальным счетчиком. Результат
высвечивается на цифровом табло. Приборы,
основанные на этом методе, называются
цифровыми тахометрами.
Обычно число
отверстий на диске и время счета импульсов
выбирают таким, чтобы число подсчитанных
импульсов за время счета было равно
числу оборотов в минуту. Так, если время
счета импульсов равно 1с, то число
отверстий на диске должно быть равно
60. Это можно пояснить на следующем
простом примере. Пусть диск совершает
1 оборот в секунду. Тогда число импульсов,
которые подсчитает прибор за 1 секунду
и высветит на табло будет равно 60, что,
очевидно, есть число оборотов диска в
минуту.
Данный способ
определения числа оборотов лишен
недостатков двух предыдущих способов,
но применение его сопряжено с иногда
непреодолимыми техническими сложностями
трудностями, связанными с размещением
диска на вращающемся объекте.
Блок-схема
установки, используемой в данной работе,
изображена на рис.2.
Электромотор
постоянного тока 3
питается от выпрямительного устройства
1,
преобразующего переменное напряжение
сети в постоянное напряжение, величина
которого плавно регулируется. Напряжение
на моторе измеряется вольтметром 2.
На валу мотора укреплен легкий диск 4
с белой радиальной полосой, необходимой
для наблюдения стробоскопического
эффекта. По краю диска высверлены 60
равноотстоящих друг от друга отверстий,
необходимых для определения числа
оборотов при помощи цифрового тахометра.
Освещение диска 4
производится импульсным осветителем
6
стробоскопического тахометра 5,
с которым осветитель связан гибким
шнуром. Отверстия на диске 4
пересекают ось фотодатчика 7,
который формирует импульсы, поступающие
на цифровой тахометр 8.
Питание
электромотора осуществляется выпрямителем
типа ВСА-5К, лицевая панель которого
изображена на рис.3.
Выпрямитель
присоединяется к сети шнуром с левой
стороны прибора, шнур справой стороны
присоединяется к электромотору. Его
Его
включение производится поворотом
тумблера 1,
вправо или влево, при этом загорается
индикаторная лампа 5.
Выходное напряжение, подаваемое к
мотору, включается тумблером 3
поворотом его влево в положение «1-я
ступень«:(“1
ст.”). Плавное
изменение выходного напряжения
осуществляется при помощи ручки 2.
В лицевую панель выпрямителя вмонтированы
измерительные приборы 4
и 6,
контролирующие выходной ток и напряжение,
которые, однако, в силу их низкой точности
они в работе не используются.
Величина
напряжения на электромоторе измеряется
универсальным вольтметром В7-16А. Им
можно определять напряжение постоянного
и переменного токов в диапазоне 110-4
— 1000 вольт и активное сопротивление в
диапазоне 0,1 – 10 7
Ом. В этой работе напряжение на
электромоторе будет изменяться в
пределах от 5
до 15В.
Погрешность определения в величины
напряжения рассчитывается по формуле
(2)
где
Ux
— измеряемое
напряжение; Uk
— предельное
напряжение в выбранном диапазоне (в
этой работе 10В или 100В).
Для
включения вольтметра установить тумблер
«сеть»
в верхнее положение. Установить тумблер
» » в положение » » (автоматический
запуск). Установить потенциометр «вр.
инд.» в
положение, обеспечивающее удобное время
индикации. После прогрева прибора
провести калибровку прибора. Для этого
установить переключатель «род
работ» в
положение «U
— 0S«,
а переключатель «предел
измерения»
— в положение «10«.
Закоротить вход «
100VR«
и ручкой «»
уста новить на индикаторном табло
показания «0000»
с равновесным изменением знака полярности;
установить переключатель «Род
работы»
в положение «»
и ручкой «»
(установка калибровки) установить на
индикаторном табло показание, равное
значению, указанному на шильдике
вольтметра.
После
калибровки для измерения напряжения
постоянного тока следует установить
переключатель «Предел
измерения»
в положение, соответствующее величине
измеряемого напряжения, а переключатель
«Род работы»
в положение «U
— 1S«. Подать
Подать
измеряемое напряжение на гнезда «
100 VR» и»0«,
произвести отсчет показаний и рассчитать
погрешность измерения по формуле (2).
Следует помнить, что при появлении
сигнала «П»
на индикаторном табло переключатель
«Предел
измерения»
надо установить в положение высшего
предела измерений.
Лицевая
панель стробоскопического тахометра
показана на рис.4. Стробоскоп присоединяется
к сети шнуром с левой стороны прибора.
Включение прибора производиться
тумблером 5
с надписью «сеть»
(при этом загорается лампочка 1).
Включение выносного импульсного
осветителя, который присоединяется
гибким шнуром к задней панели прибора,
производится тумблером 6
с надписью «лампа«.
Зажигание осветителя производится
тумблером 7.
На шкале 2
прибора имеется 7 диапазонов (они
обозначены буквами от А
до Ж),
на которые разделен весь интервал частот
от 250 до 32000 вспышек в минуту. Переключение
диапазонов производится тумблером 3.
Внутри каждого диапазона частоту
изменяют с помощью ручки (верньера) 4,
расположенного под шкалой.
Измерение
частоты вращения диска (точнее вала
мотора, на котором укреплен диск)
производится так. Осветив диск выносным
осветителем, подбирают, вращая ручки 3
и 4,
частоту вспышек так, чтобы белая черта
на диске казалась неподвижной. Можно
выбрать и такую частоту вспышек, при
которой видно несколько неподвижных
белых полос с одинаковыми углами между
ними. В этом случае, если точно известно,
что число вспышек больше числа оборотов,
отсчитанная по прибору частота вспышек
больше частоты вращения в число раз
равное числу неподвижных полос.
В
работе также используется цифровой
тахометр ТЦ-3М. Пределы измерения его —
10
20000об/мин,
погрешность измерения числа оборотов
— 3об/мин.
Измерения числа оборотов при помощи
этого прибора чрезвычайно просто. На
его табло, сразу после включения и 10-ти
минутного прогрева, высвечивается
периодически в течение 1секунды значение
числа оборотов в предыдущую секунду.
ПОРЯДОК
ВЫПОЛНЕНИЯ РАБОТЫ И УСЛОВИЯ ЭКСПЕРИМЕНТА
Перед
началом выполнения работы следует
внимательно ознакомиться с приборами.
1.
Включите вольтметр в сеть и проведите
калибровку прибора.
2.
Включите выпрямительное устройство в
сеть. Ручку 2
выверните
вращением против часовой стрелки в
крайнее левое положение, включите
выпрямитель тумблером 1.
Поставьте тумблер 3
в положение «1
ступень »
(1ст.).
Вращением ручки плавного изменения
напряжения 2
приведите мотор во вращение. Убедитесь
в том, что вращением этой ручки можно
изменять частоту вращения мотора. По
вольтметру следите за тем, чтобы
напряжение не превышало 15 вольт.
3.
Включите в сеть цифровой тахометр.
Включите тумблер
с надписью
«сеть«.
4.
Включите в сеть строботахометр. Включите
тумблер 5 с
надписью «сеть«.
Через несколько минут включите питание
осветителя тумблером 6
с надписью «лампа«.
Направив осветитель на вращающийся
диск, изменяя частоту вспышек, наблюдайте
стробоскопический эффект.
5.
Проведите измерения частоты вращения
вала мотора при помощи цифрового и
стробоскопического тахометров в
зависимости от приложенного к мотору
напряжения. Для этого, изменяя напряжения,
приложенное к электромотору от 5
до 15
вольт с шагом
1
вольт, проведите измерение частоты
вращения вначале цифровым, а затем
стробоскопическим тахометрами. При
каждом значении напряжения, которое
отсчитывается по вольтметру необходимо
провести не менее 5-7 измерений каждым
способом. Результаты измерений числа
оборотов удобно представить в виде
таблицы, приведенной ниже.
Таблица 1
Результаты измерений
частоты вращения вала электромотора
|
U, В |
n1, об/мин |
n2 об/мин |
n3 об/мин |
n4 об/мин |
n5 об/мин |
n, |
n, об/мин |
с об/мин |
n, об/мин |
|
|
Цифровой тахометр |
||||||||||
|
Стробоскоп. тахометр |
ОБРАБОТКА РЕЗУЛЬТАТОВ
ЭКСПЕРИМЕНТА
В
последних 4-х столбцах табл.1 приводятся
расчетные величины — среднее значение
частоты вращенияn,
при данном напряжении
U, случайная
погрешность измерений °
n,
систематическая погрешность измерений
с
n,
наконец, полная погрешность. Величина
°
n
рассчитывается в соответствии с правилами
обработки прямых измерений. Значение
c
n
определяется по классу точности приборов.
Класс точности строботахометра приведен
на задней крышке прибора. Относительную
допускаемую погрешность механического
тахометра следует принять равной 5%.
Для
дальнейшего анализа экспериментальные
результаты необходимо представить в
виде графиков зависимости угловой
скорости от напряжения U
на электромоторе. Следует помнить, что
экспериментальные точки на графиках
должны иметь «размер». Этот «размер»
определяется погрешностями результатов
измерений. В данной работе размер точек
на графике по оси абсцисс равен погрешности
результата измерения напряжения (она
вычисляется по формуле (2)), а по оси
ординат — погрешности определения
угловой скорости. Таким образом, «точки»
на графике экспериментальной зависимости
должны представлять собой прямоугольную
область, которая задается четырьмя
точками (U-U,
—),
(U-U,
+),
(U+U,
+)
и (U+U,
—).
Понятно, что экспериментальные точки
удобно изображать прямоугольниками
или крестиками.
Прежде
чем приступить к построению графиков
необходимо по данным табл. 1 рассчитать
1 рассчитать
значения угловой скорости
и ее погрешности
и занести
их в таблицу, примерный вид который
приведен ниже.
Таблица 2
|
U, |
U, |
Цифровой тахометр |
Стробоскопический |
||
|
, |
, |
, |
, |
||
Используя
данные табл. 2 надо построить в одних и
2 надо построить в одних и
тех же координатных осях два графика
зависимости
=(U).
Первый — это график зависимости угловой
скорости вала мотора, рассчитанной по
показаниям цифрового тахометра, от
напряжения на электромоторе. Второй —
это график аналогичной зависимости
угловой скорости, но рассчитанной по
показаниям стробоскопического тахометра.
Естественно, что экспериментальные
точки на разных графиках должны
изображаться по-разному.
Теперь
необходимо проанализировать вид
зависимости
=(U),
а также сделать обоснованный вывод о
степени соответствия результатов
измерений, полученных разными способами.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое
угловая скорость и частота вращения? В
каких единицах они измеряются?
2.
В чем состоит стробоскопический эффект,
используемый для измерения частоты
вращения?
3.
Каков будет стробоскопический эффект,
если частота вспышек импульсного
осветителя в полтора раза больше частоты
вращения? В полтора раза меньше частоты
вращения
Движение по окружности.
 Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости
Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости
|
|
|||||||||||||||||||||||
|
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление
|
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Движение по окружности. Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
||||||||||||||||||||||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. |
|||||||||||||||||||||||
|
Коды баннеров проекта DPVA.ru Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator |
||||||||||||||||||||||
Как рассчитать угловую частоту
Обновлено 16 декабря 2020 г. по кругу измеряет скорость, с которой мяч проходит полные 360 градусов, или 2π радиан. Самый простой способ понять, как рассчитать угловую частоту, — построить формулу и посмотреть, как она работает на практике.
Формула угловой частоты
Формула угловой частоты представляет собой частоту колебаний f (часто в единицах Герц, или колебаний в секунду), умноженную на угол, под которым движется объект. Формула угловой частоты для объекта, который совершает полное колебание или вращение, выглядит следующим образом:
\omega = 2\pi f
Более общая формула выглядит просто:
\omega = \frac{\theta}{t}
где θ — угол, на который перемещался объект, а t — это время, которое потребовалось, чтобы пройти через θ .
Помните: частота — это скорость, поэтому размерность этой величины — радианы в единицу времени. Единицы будут зависеть от конкретной проблемы. Если вы говорите о вращении карусели, вы можете говорить об угловой частоте в радианах в минуту, но угловая частота Луны вокруг Земли может иметь больше смысла в радианах в день.
Единицы будут зависеть от конкретной проблемы. Если вы говорите о вращении карусели, вы можете говорить об угловой частоте в радианах в минуту, но угловая частота Луны вокруг Земли может иметь больше смысла в радианах в день.
-
Угловая частота — это скорость, с которой объект перемещается на определенное количество радиан. Если известно время, за которое объект прошел угол, угловая частота равна углу в радианах, деленному на время, затраченное на это.
Формула угловой частоты с использованием периода
Чтобы полностью понять эту величину, полезно начать с более естественной величины, периода и работать в обратном порядке. Период ( T ) колеблющегося объекта – это время, необходимое для совершения одного колебания. Например, в году 365 дней, потому что именно столько времени требуется Земле, чтобы совершить один оборот вокруг Солнца. Это период обращения Земли вокруг Солнца.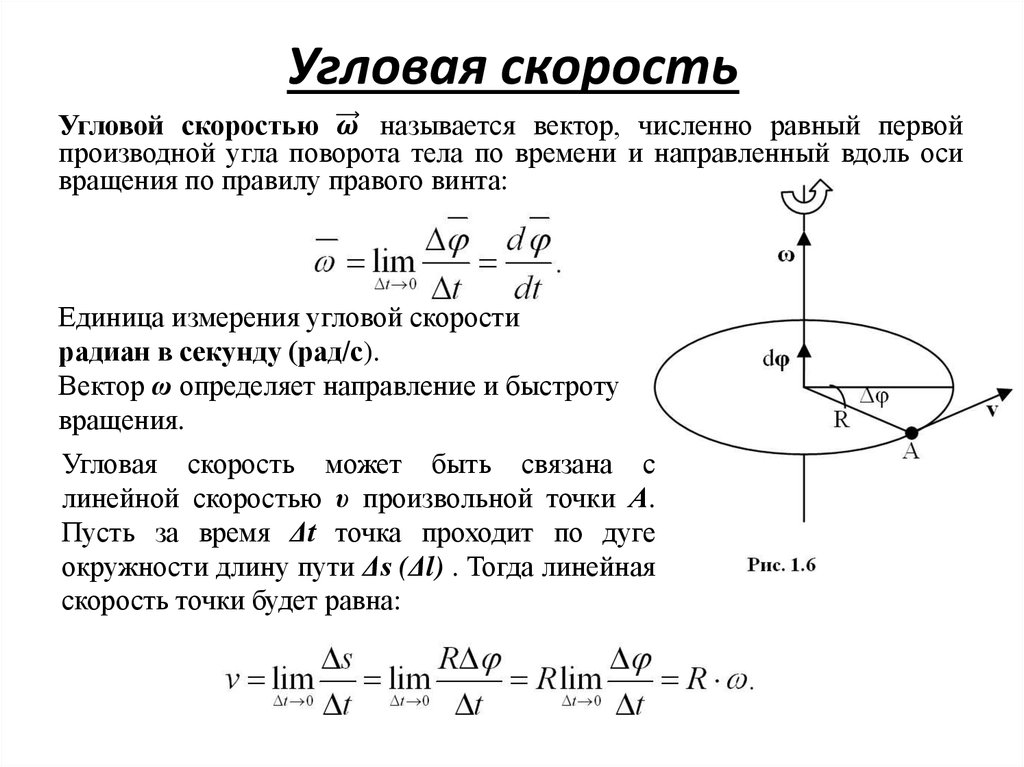
Но если вы хотите узнать скорость вращения, вам нужно найти угловую частоту. Частоту вращения или количество оборотов за определенный промежуток времени можно рассчитать по формуле:
f=\frac{1}{T}
Для Земли один оборот вокруг Солнца занимает 365 дней, так что f = 1/365 дней.
Так что такое угловая частота? Один оборот Земли совершает 2π радиан, поэтому угловая частота ω = 2π/365. Другими словами, Земля проходит 2π радиан за 365 дней.
Пример расчета
Попробуйте другой пример расчета угловой частоты в другой ситуации, чтобы привыкнуть к понятиям. Поездка на колесе обозрения может длиться несколько минут, за это время вы несколько раз достигаете вершины аттракциона. Допустим, вы сидите на вершине колеса обозрения и замечаете, что колесо сделало четверть оборота за 15 секунд. Какова его угловая частота? Есть два подхода, которые вы можете использовать для расчета этого количества.
Во-первых, если ¼ оборота занимает 15 секунд, полный оборот занимает 4 × 15 = 60 секунд. Следовательно, частота вращения f = 1/60 с −1 , а угловая частота:
\begin{aligned} ω &= 2πf \\ &= π/30 \end{aligned }
Точно так же вы прошли π/2 радиана за 15 секунд, поэтому снова, используя наше понимание того, что такое угловая частота:
\begin{aligned} ω &= \frac{(π/2)}{15 } \\ &= \frac{π}{30} \end{выровнено}
Оба подхода дают один и тот же ответ, так что, похоже, наше понимание угловой частоты имеет смысл!
И последнее…
Угловая частота — это скалярная величина, то есть это просто величина. Однако иногда мы говорим об угловой скорости, которая является вектором. Следовательно, формула угловой скорости совпадает с уравнением угловой частоты, которое определяет величину вектора.
Тогда направление вектора угловой скорости можно определить с помощью правила правой руки.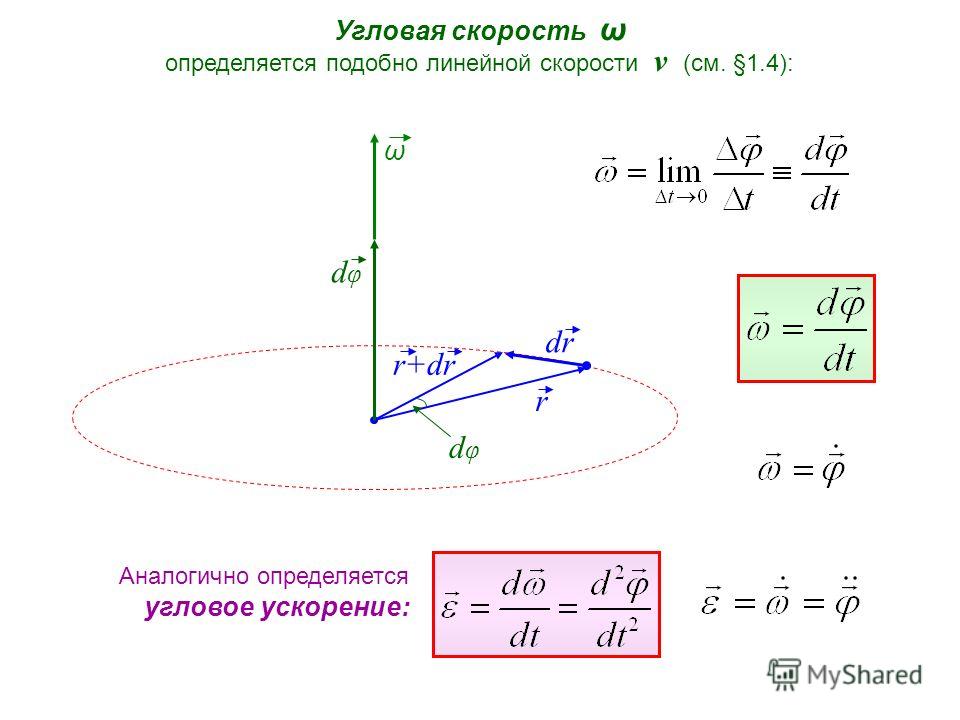 Правило правой руки позволяет нам применять соглашение, которое физики и инженеры используют для определения «направления» вращающегося объекта.
Правило правой руки позволяет нам применять соглашение, которое физики и инженеры используют для определения «направления» вращающегося объекта.
ньютоновская механика — Почему угловая скорость и угловая частота не измеряются в герцах?
спросил
Изменено
3 года, 7 месяцев назад
Просмотрено
1к раз
$\begingroup$
Недавно я делал домашнее задание и обнаружил, что угловую скорость и угловую частоту можно рассчитать с помощью $\omega=v/r$. Это означает, что единицами угловой скорости и угловой частоты являются (метр/секунда)/метр или 1/секунда. Частота вращения также измеряется в $1/с$, то есть в Гц.
Однако угловая частота отличается от обычной частоты. Я действительно смущен, почему это не измеряется в герцах.
Я действительно смущен, почему это не измеряется в герцах.
- ньютоновская механика
- единиц
- частота
- размерный анализ
- угловая скорость
$\endgroup$
3
$\begingroup$
Предполагаемое значение единицы герц состоит в том, что один герц соответствует одному полное возникновение циклического явления за одну секунду. Угловая частота — это не число полных оборотов, происходящих в единицу времени, а углов, покрываемых за эту единицу времени. Технически, угловая частота равна , а не , измеренной в
$$\frac{\mathrm{1}}{\mathrm{s}}$$
, а вместо этого в
$$\frac{\mathrm{rad}} {\mathrm{s}}$$
, то есть радиан в секунду, поэтому угол поворачивается за единицу времени. Однако, поскольку радиан определяется как безразмерный, эти два равны математически эквивалентно .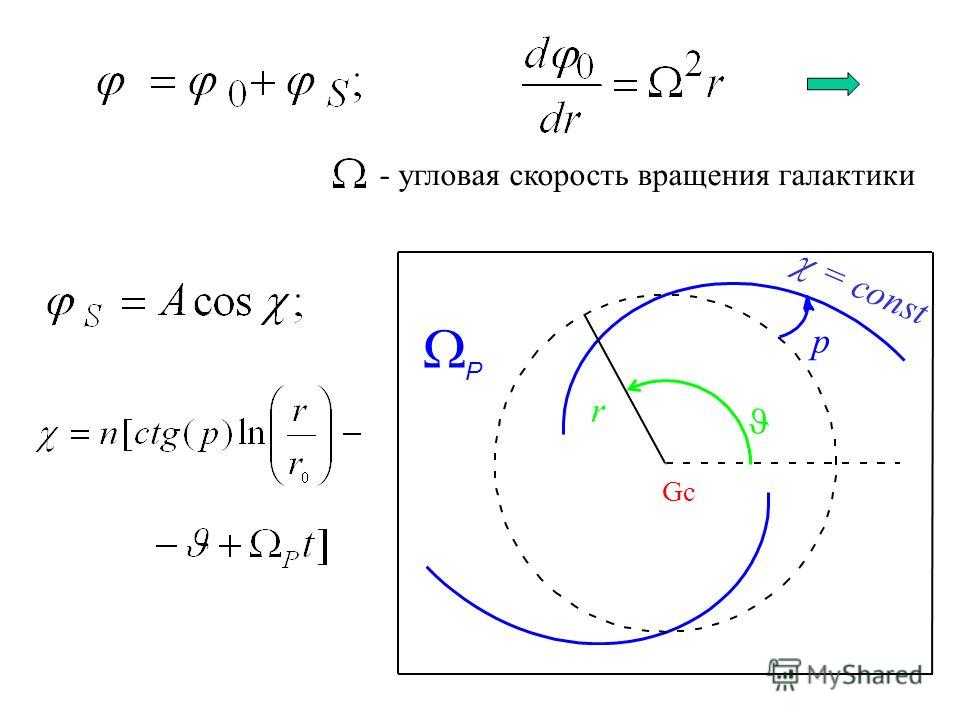

 Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости
Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости:
Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости: Введите свой запрос:
Введите свой запрос: