Содержание
Асинхронные электродвигатели (страница 2)
1. Определить угловую скорость вращении ротора асинхронного электродвигателя, если обмотка статора четырехполюсная, частота напряжения сети, к которой присоединен электродвигатель, 50 Гц и скольжение ротора равно 3,5%.
Решение:
Частота токов, проходящих в обмотках статора, равна частоте напряжения сети:
Кроме того, известно, что обмотка статора четырехполюсная, т. е. число пар полюсов р = 2.
Скорость вращения магнитного потока, вызываемого трехфазной системой токов, проходящих в обмотках статора, зависит от частоты этих токов
и числа пар полюсов обмотки р, так как , откуда число оборотов в минуту вращающегося синхронно магнитного потока
Угловая скорость вращения
Вращение ротора асинхронного электродвигателя возможно лишь при наличии отставания ротора от вращающегося магнитного потока. Величина, характеризующая это отставание, называется скольжением:
где
— скорость вращения магнитного потока;
— скорость вращения ротора.
Подставив числовые значения, получим
откуда
Угловая скорость вращения ротора
2. На щитке асинхронного электродвигателя значится: 730 об/мин, 50 Гц.
Определить скольжение ротора, вращающегося с указанной скоростью, и число пар полюсов обмотки статора. Каким было скольжение ротора в первые мгновения пуска?
Решение:
В табл. 13 синхронных скоростей вращения при частоте 50 Гц ближайшей скоростью вращения (по отношению к скорости
) является скорость .
Следовательно, скольжение ротора
Число пар полюсов обмотки статора
Число полюсов
В момент пуска ротор неподвижен
. Поэтому скольжение при пуске
Такое значение имеет скольжение ротора в момент пуска любого асинхронного электродвигателя.
Таблица 13
р пар полюсов | 1 | 2 | 3 | 4 | 5 |
n, об/мин | 3000 | 1500 | 1000 | 750 | 600 |
3.
В разрыв провода линии, соединяющей контактные кольца ротора асинхронного электродвигателя с трехфазным реостатом, введен магнитоэлектрический амперметр, шкала которого имеет нулевое значение посередине (рис. 80). Разомкнув рубильник, шунтировавший амперметр во время разбега ротора, не поднимая щеток, наблюдали за отклонениями амперметра: оказалось, что за полминуты указательная стрелка прибора совершила 60 полных колебаний.
Определить скорость вращения ротора в течение указанного промежутка времени, если обмотка статора шестиполюсная и частота напряжения сети 50 Гц.
Решение:
Полное колебание указательной стрелки соответствует полному периоду тока в обмотке ротора. Если 60 полных колебаний (периодов) произошло за полминуты, то число полных колебаний (периодов) в секунду равно двум. Следовательно,
Магнитный поток в асинхронном электродвигателе вращается относительно ротора со скоростью, равной разности скоростей:
причем частота тока в роторе
Подставив числовые значения, получим
При шестиполюсной обмотке статора и частоте токов в цепи статора
скорость вращения магнитного потока
Подставим в выражение для
величины
откуда скорость вращения ротора
Скольжение ротора
4.
Когда трехфазный асинхронный двигатель с фазным ротором присоединили к сети с линейным напряжением 220 В, напряжение между контактными кольцами при разомкнутой обмотке ротора составило 90 В.
Определить коэффициент трансформации, рассматривая этот электродвигатель как трансформатор в режиме холостого хода, если обмотки статора и ротора соединены звездой.
Решение:
Фазное напряжение на обмотке статора при схеме соединения звездой в
раз меньше линейного напряжения. Следовательно,
Фазное напряжение на обмотке ротора
Коэффициент трансформации фазных напряжений
5. Асинхронный электродвигатель с короткозамкнутым ротором характеризуется отношением вращающих моментов соответственно при пуске и при номинальном режиме
.
Можно ли осуществить пуск двигателя в случае полной его нагрузки на валу и понижения напряжения в сети на 5 и 10%? К сети присоединен статор.
Решение:
Вращающий момент асинхронного двигателя прямо пропорционален квадрату напряжения в сети:
Следовательно, если напряжение в сети понизится на 5% и составит
, то вращающий момент
Отношение
Так как пусковой момент при номинальном напряжении , то при понижении напряжения в сети на 5% пусковой момент
Таким образом, пуск при этих условиях позволит электродвигателю развить вращающий момент больше номинального.
Если напряжение в сети понизится на 10% и составит
, то вращающий момент
Пусковой момент при указанном понижении напряжения
Обозначим через
долю, которую составляет пусковой вращающий момент от вращающего момента при номинальном напряжении. Тогда для возможности пуска электродвигателя при номинальной нагрузке должно быть выполнено равенство
Поэтому при пуске электродвигателя напряжение сети может составлять от номинального напряжения долю
Таким образом, при заданной кратности пускового момента от номинального
понижение напряжения в сети может происходить на и пуск может быть осуществлен при номинальной нагрузке на валу электродвигателя.
6. Асинхронный электродвигатель с короткозамкнутым ротором типа А51-4 имеет следующие номинальные данные:
; кратность вращающих моментов .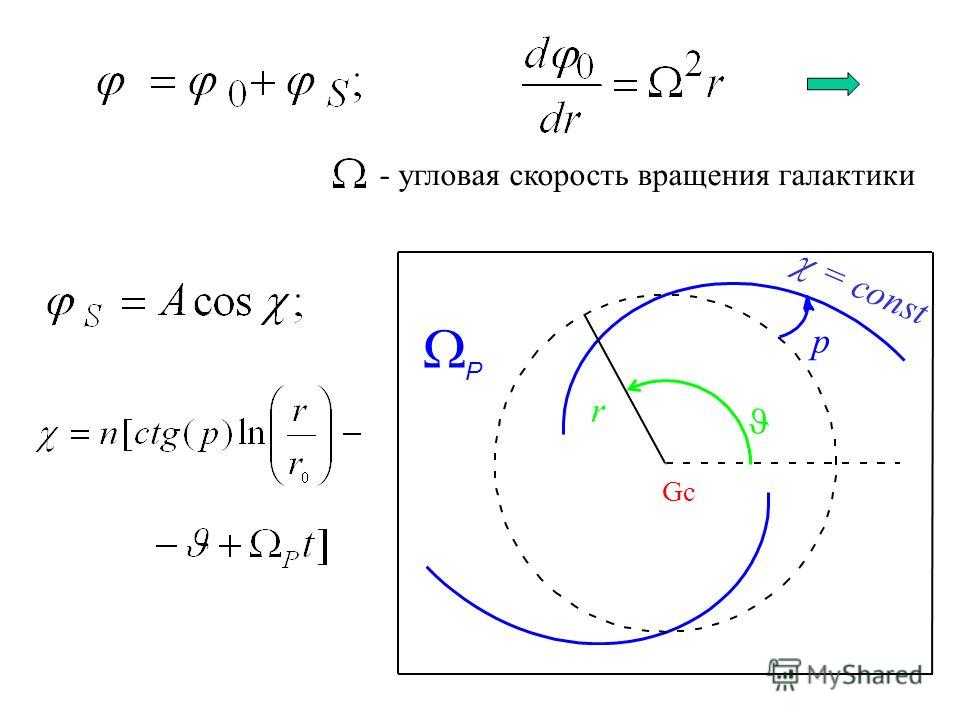
Определить вращающие моменты: номинальный
, максимальный и пусковой .
Решение:
Номинальный вращающий момент можно определить из основного соотношения
Вращающий момент
измерен в и мощность Р — в Вт. При этом
Если подставить сюда в качестве Р мощность, измеренную в киловаттах, то число будет в 1000 раз меньше.
Таким образом, при тех же единицах измерения вращающего момента получим
Подставим величины номинального режима:
Используя известные кратности моментов, максимальный вращающий момент
пусковой вращающий момент
7. Асинхронный электродвигатель развивает номинальную мощность
при номинальной скорости вращения ротора , имея перегрузочную способность 2,1.
Выразить зависимость между вращающим, моментом и скольжением ротора S электродвигателя.
Решение:
Номинальный вращающий момент
Перегрузочная способность l = 2,1 представляет собой отношение максимального вращающего момента
к номинальному вращающему моменту .
Следовательно,
Номинальному вращающему моменту соответствует и номинальное скольжение
где в качестве
подставлена ближайшая большая (по отношению к ) синхронная скорость вращения магнитного потока статора.
Зависимость между вращающим моментом и скольжением ротора s в асинхронном двигателе выражается формулой
где
означает критическое скольжение, а и s соответствуют одному и тому же режиму работы. Если в левую часть подставить , то в качестве s следует подставить . Тогда можно определить критическое скольжение , при котором имеет место момент . В этом случае получается квадратное уравнение, из которого берут большее значение корня.
Так как
Разделив на 0,238 левую и правую части равенства и сосредоточив все члены в одной стороне, получим
Корни полученного квадратного уравнения
Далее берется только больший из корней (при положительном знаке перед корнем):
Подставив в формулу, выражающую зависимость между вращающим моментом
и скольжением ротора s, численные значения , получим требуемую зависимость
7.
2. Вращательное движение. Угловая скорость, угловое ускорение
Движение
твердого тела, при котором все его точки
перемещаются по окружности, центры
которой расположены на перпендикулярной
этим окружностям неподвижной прямой,
называется вращательным.
Неподвижная прямая, на которой лежат
центры круговых траекторий точек
тела, называется его осью
вращения.
Для образования оси вращения достаточно
закрепить какие-либо две точки тела. В
качестве примеров вращательного движения
тел можно привести движение дверей
или створок окон при их открывании или
закрывании.
Представим
себе тело в виде цилиндра, ось AB
которого лежит в подшипниках (рис. 7.3).
Рис. 7.3. К
анализу вращательного движения твердого
тела
Движением одной
какой-либо точки однозначно определить
вращательное движение тела нельзя.
Для
установления закона вращательного
движения тела, по которому можно
определять его положение в данный
момент, проведем через ось вращения
тела связанную только с нею неподвижную
полуплоскость НП, а внутри тела отметим
подвижную полуплоскость, которая
вращается около оси вместе с телом,
теперь угол
φ,
образуемый в каждый данный момент
времени полуплоскостями НП и ПП, точно
определяет положение тела в пространстве
(см.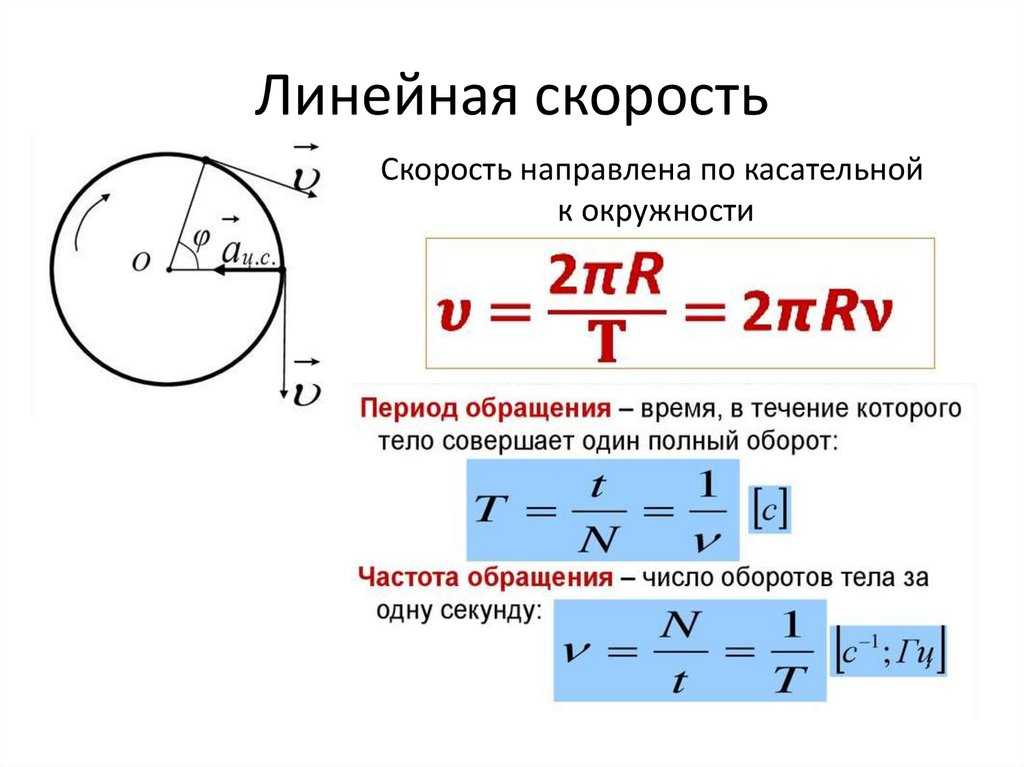
рис. 7.3). Угол φ
называется углом
поворота
и выражается в радианах. Чтобы определять
положение тела в пространстве в любой
момент времени, необходимо знать
зависимость между углом поворота φ
и временем t,
т. е. знать закон вращательного движения
тела:
Быстрота
изменения угла поворота во времени
характеризуется величиной, которая
называется угловой
скоростью.
Представим,
что в некоторый момент времени t
положение
вращающегося тела определяется углом
поворота φ,
а в момент t
+ Δt –
углом поворота φ
+ Δ φ.
Следовательно, за время Δt
тело повернулось на угол Δ
φ,
и величина
называется
средней
угловой скоростью.
Единицей
угловой скорости является 1 рад/с.
Характеристикой быстроты изменения
угловой скорости служит угловое
ускорение,
обозначаемое
.
Среднее ускорение
;
.
Единица
углового ускорения 1 рад/с2.
Условимся
угол поворота, отсчитываемый против
хода часовой
стрелки,
считать положительным, а отсчитываемый
по ходу часовой стрелки – отрицательным.
б
а
Рис. 7.4. К
определению вида вращательного движения
Векторы
и
– это скользящие векторы, которые
направлены по оси вращения, чтобы, глядя
из конца вектора
(или
),
видеть вращение, происходящее против
часовой стрелки.
Если
векторы
и
направлены в одну сторону (рис. 7.4,
а),
то вращательное движение тела ускоренное
– угловая скорость возрастает. Если
векторы
и
направлены в противоположные стороны,
то вращение тела замедленное
–
угловая скорость уменьшается (рис. 7.4,
б).
1. Равномерное
вращательное движение.
Если угловое ускорение
и, следовательно, угловая скорость
,
(7.1)
то
вращательное движение называется
равномерным. Из выражения (7.1) после
разделения переменных получим
Если
при изменении времени от 0 до t
угол поворота изменялся от φ0
(начальный угол поворота) до φ,
то, интегрируя уравнение в этих пределах:
получаем уравнение
равномерного вращательного движения
,
которое в
окончательном виде записывается так:
.
Если
,
то
.
Таким
образом, при равномерном вращательном
движении угловая скорость
или при
.
2. Равнопеременное
вращательное движение.
Если угловое ускорение
(7.2)
то
вращательное движение называется
равнопеременным.
Производя разделение
переменных в выражении (7.2):
и
приняв, что при изменении времени от 0
до t
угловая скорость изменилась от
(начальная угловая скорость) до
,
проинтегрируем уравнение в этих пределах:
или
,
т. е.
получим уравнение
(7.3)
выражающее значение
угловой скорости в любой момент времени.
Закон
равнопеременного вращательного движения
или, с учетом уравнения (7.3):
Полагая,
что в течение времени от 0 до t
угол поворота изменялся от
до,
проинтегрируем уравнение в этих пределах:
или
Уравнение
равнопеременного вращательного движения
в окончательном виде
(7.4)
Первую
вспомогательную формулу получим,
исключив из формул (7.
3)
и
(7.4) время:
(7.5)
Исключив
из тех же формул угловое ускорение
,
получим вторую вспомогательную формулу:
(7.6)
где
–
средняя угловая скорость при
равнопеременном вращательном
движении.
Когда
и
,
формулы (7.3)–(7.6) приобретают более
простой вид:
В
процессе конструирования угловое
перемещение выражают не в радианах, а
просто в оборотах.
Угловая
скорость, выражаемая количеством
оборотов в минуту, называется частотой
вращения
и обозначается n.
Установим зависимость между
(с–1)
и n
(мин–1).
Так как
,
то при n
(мин–1)
за t
=
1 мин = 60 с угол поворота
.
Следовательно:
.
При
переходе от угловой скорости
(с–1)
к частоте вращения n
(мин–1)
имеем
Равномерное круговое движение
Введение
Равномерное круговое движение — это движение объекта, движущегося с постоянной (равномерной) скоростью по круговой траектории.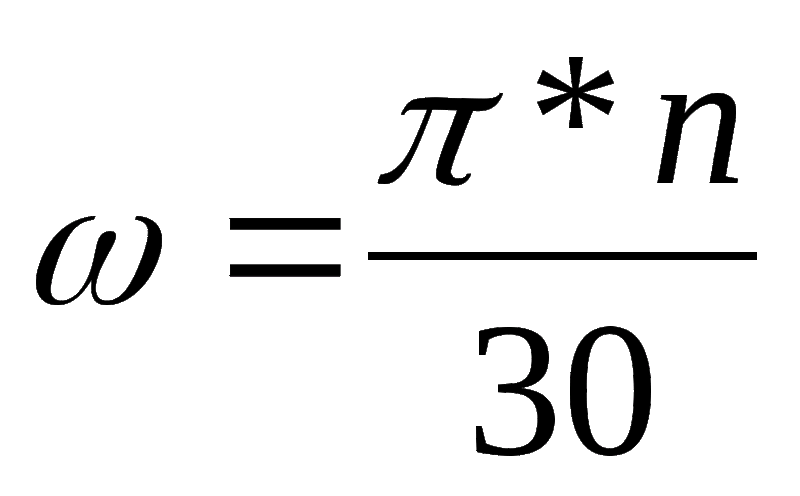
Помимо скорости, есть несколько других переменных, которые используются для характеристики движения. Это радиус движения r , угловая скорость ω , период T и частота вращения f . Период — это время, необходимое объекту для совершения одного оборота движения. угловая скорость представляет собой угловое смещение в секунду и связано с частотой соотношением:
( 1 )
ω = 2 π f
с ω в рад/с.
Частота вращения представляет собой число оборотов в секунду и определяется по формуле:
( 2 )
f =
с f в Гц или с -1 .
скорость объекта касается окружности с величиной v = rω . Ускорение , a направлено к центру окружности (центростремительной) с величиной, определяемой как:
( 3 )
а = = r ω 2
с a в м/с 2 .
Чтобы объект массой м мог двигаться по окружности с постоянной скоростью, на объект должна действовать результирующая центростремительная сила. Величина чистой силы, F , должно быть постоянным и связано с центростремительным ускорением вторым законом Ньютона:
( 4 )
F = ma = mr ω 2
с F в Н.
Эта центростремительная сила может быть обеспечена натяжением (как в этой лаборатории), трением (как в случае с автомобилем, огибающим кривую), нормальной силой (как в петлевых американских горках) или гравитацией (как в случае движения спутника). В этом эксперименте вы измерите период равномерного кругового движения объекта с фиксированным радиусом, но с различными значениями Ф . По периоду можно рассчитать угловую скорость. С этими известными значениями и приведенными выше уравнениями вы можете найти эмпирическую массу вращающегося объекта и сравнить со значением массы, найденным путем непосредственного взвешивания на весах.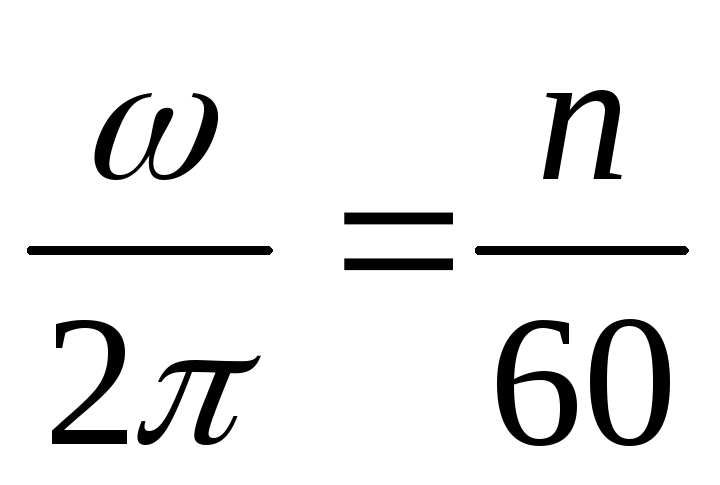
Аппарат UCM
Устройство UCM состоит из вращающейся платформы с регулируемой скоростью . Расстояние r от центра вращения составляет боковую стойку в сборе , на которой висит объект массой м , именуемая вращающейся массой (не путать со статической массой ). Вращающаяся масса прикреплена к пружине на центральной стойке с помощью веревки и небольшого шкива. Когда платформа вращается, вращающаяся масса перемещается по круговым траекториям из-за силы, действующей на нее со стороны струны (за счет натяжения пружины). Поскольку невозможно получить мгновенные показания этой силы натяжения во время вращения платформы, будет выполнено косвенное измерение этой силы с использованием веса статической массы, как показано и объяснено ниже.
Рисунок 1
Когда платформа не вращается, вращающаяся масса не висит вертикально на боковой стойке, а скорее втягивается внутрь за счет натяжения струны и пружины.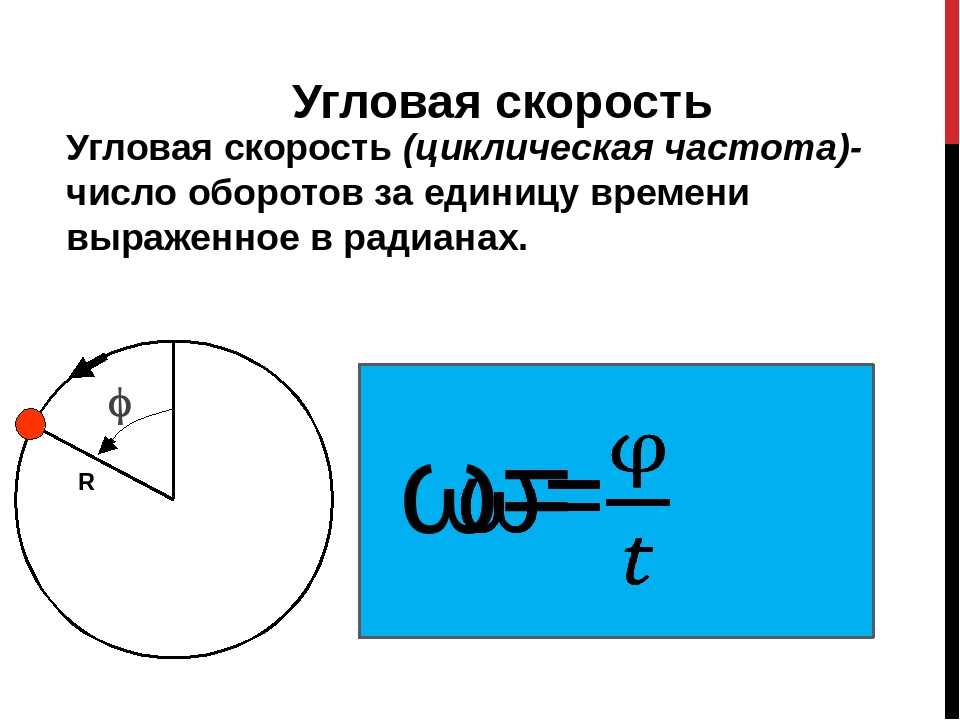
При выполнении эксперимента вы будете регулировать скорость вращения платформы до тех пор, пока вращающаяся масса не будет висеть вертикально на радиусе r . Оранжевый индикаторный диск поможет вам определить, когда вращающаяся масса достигла этого положения.
Рисунок 2
Период вращения измеряется секундомером . Платформу можно вращать, поворачивая стержень с накаткой вручную.
Процедура
Выравнивание аппарата
Если платформа не выровнена, это отрицательно скажется на ваших результатах. Студенты в первой лаборатории недели уже должны были выровнять аппарат. Будем надеяться, что с тех пор аппарат не перемещался и его не нужно будет снова выравнивать. Проверьте, выровнено ли ваше устройство, включив двигатель регулятора скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы.
Если ваше устройство необходимо выровнять, выполните следующие действия.
1
Чтобы примерно выровнять платформу, поместите пузырьковый уровень в середину платформы и отрегулируйте два регулировочных винта на основании устройства, пока пузырьковый уровень не окажется в центре.
2
Поместите дополнительную массу (~ 500 г) на тот же конец вращающейся платформы, что и вращающаяся масса. Если платформа не выровнена, тяжелый конец будет качаться в сторону, которая ниже.
3
Отрегулируйте регулировочные винты на ножках основания так, чтобы конец платформы качался равномерно при легком вращении рукой.
Настройка радиуса
1
Осторожно отцепите вращающуюся массу от струн. Используйте весы, чтобы взвесить его, и запишите значение массы.
2
Подвесьте вращающуюся массу к боковой стойке и подсоедините струну от пружины к массе. Убедитесь, что эта струна проходит под (а не за) маленьким шкивом на центральной стойке.
3
Переместите скобу индикатора на центральной стойке в крайнее нижнее положение.
4
Оттягивайте вращающуюся массу от центральной стойки до тех пор, пока оранжевый индикатор не окажется в центре кронштейна. Если струна, поддерживающая вращающуюся массу, не является вертикальной, когда индикатор совмещен с кронштейном, боковую стойку следует перемещать внутрь или наружу до тех пор, пока струна не станет вертикальной. Используйте вертикальную линию на боковой стойке, чтобы помочь в этом выравнивании. При затягивании боковой стойки
надавите на платформу, чтобы убедиться, что она надежно удерживается в вертикальном положении, и избегайте чрезмерного затягивания и поломки пластикового винта с накатанной головкой!5
Измерьте и запишите радиус вместе с оценкой неопределенности на основе выравнивания.
6
Теперь ваш аппарат должен быть готов к максимально широкому диапазону центростремительных сил.
(Почему это важно?) Центростремительная сила будет изменяться путем перемещения пружинной опоры вверх и вниз, удерживая при этом другие части аппарата на месте. Этот диапазон
перемещения по центральной стойке должно быть не менее 5 см, что соответствует диапазону натяжения пружины примерно 1,2 Н.
(Почему это важно?) Центростремительная сила будет изменяться путем перемещения пружинной опоры вверх и вниз, удерживая при этом другие части аппарата на месте. Этот диапазонНастройка величины центростремительной силы
В этой первой части процедуры вы будете использовать статический метод (без вращения) для настройки аппарата на известное значение центростремительной силы.
1
Прикрепите зажимной шкив к концу платформы, ближайшему к вращающейся массе. Прикрепите веревку к вращающейся массе и повесьте известную массу (начните с 20 г) на зажимной шкив. Отрегулируйте зажимной шкив вверх или вниз по мере необходимости, чтобы струна между шкивом и
вращающаяся масса горизонтальна. (Почему это важно?)2
Запишите значение этой статической массы , которая будет определять центростремительную силу.
3
Отрегулируйте опору пружины по вертикали, пока оранжевый индикаторный диск не окажется в центре кронштейна индикатора. Устройство теперь должно быть выровнено, чтобы точно знать радиус движения вращающейся массы, когда платформа вращается.
В этот момент остановитесь и проанализируйте все силы, действующие на вращающуюся массу. Каковы их величины и направления? Какая из сил не совсем вертикальная или горизонтальная? Если да, то как это повлияет на ваши результаты?
КПП 1:
Попросите вашего ассистента проверить ваше устройство, прежде чем продолжить.
Измерение периода
1
Снимите статическую массу и струну с вращающейся массы. (Почему?)
2
Вращайте аппарат, медленно медленно поворачивая рифленый стержень по часовой стрелке. Потратьте минуту, чтобы получить хорошее представление о повороте платформы с постоянной скоростью.
Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется в центре кронштейна индикатора на центральной стойке. Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна, и, следовательно, масса находится на желаемом радиусе.3
Когда один партнер по лаборатории вращает платформу, другой должен использовать секундомер для измерения времени, необходимого для совершения одного оборота. Сделайте десять таких измерений.
4
Альтернативным методом измерения среднего периода является использование секундомера для измерения времени N (например, 10) оборотов и деление на N, чтобы получить T . Сделайте это хотя бы в одном испытании и сравните со значением, полученным с помощью процедуры, описанной в шаге 3. Какой метод вы считаете более точным?
5
Прежде чем продолжить, проверьте свои результаты для этой одной точки данных и убедитесь, что ваше эмпирическое значение для вращающейся массы разумно.
Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.
Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется в центре кронштейна индикатора на центральной стойке. Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна, и, следовательно, масса находится на желаемом радиусе.
Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные. КПП 2:
Попросите вашего ТА проверить ваши данные и результаты расчетов, прежде чем продолжить.
Изменение центростремительной силы
Повторите описанную выше процедуру, по крайней мере, с пятью различными статическими массами (и, следовательно, с пятью различными силами), которые охватывают самый широкий диапазон значений (обычно от 40 до 150 г).
Анализ
1
Вес статической массы, висящей над шкивом, равен центростремительной силе F , приложенной пружиной. Рассчитайте эту силу для каждого из ваших пяти испытаний, умножив статическую массу на г , и запишите результаты.
2
Для каждой центростремительной силы F рассчитайте средний период вращения T и его стандартную ошибку.
3
Для каждого значения F вычислить ω 2 и его неопределенность из
ω = .
4
Постройте ω 2 против F (с планками погрешностей) и выполните линейную подгонку методом наименьших квадратов.
5
Определите экспериментальное значение вращающейся массы, м , по наклону графика и уравнению центростремительной силы. Определите y -пересечение линейной подгонки к вашим данным. Это то, что вы ожидаете, что это должно быть?
Обсуждение
Сравните значение м , полученное из вашей кривой, с измеренными значениями вращающейся массы м и радиуса движения r . Есть ли согласие в пределах неопределенностей? Если вы тщательно проведете этот эксперимент, вы сможете получить результаты с ошибкой менее 3%.
Сравните значение y -перехват с ожидаемым значением.
Они согласны?
Почему для этого (и большинства других) экспериментов важно получать данные в максимально широком диапазоне значений? Каковы потенциальные последствия наличия точек данных, которые расположены близко друг к другу?
Объясните, как вы будете получать данные с помощью этого прибора, чтобы проверить следующую гипотезу: при заданном значении величины центростремительной силы F радиус движения r обратно пропорционален квадрату угловой скорости ω .
Преобразователь случайных чисел | Преобразователь угловой скорости и частоты вращения Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. От: радиан/секундарадиан/деньрадиан/часрадиан/минутаградус/деньградус/часградус/минутаградус/секундаоборот/деньоборота/часоборота/минутаоборот/секундоворот/годоборот/месяцоборот/неделяградус/годградус/месяцградус/неделярадиан/годрадиан/месяцрадиан/неделя Кому: радиан/секунда радиан/деньрадиан/часрадиан/минутаградус/деньградус/часградус/минутаградус/секундаоборота/деньоборота/часоборота/минутаоборота/секундаоборота/годоборот/месяцоборот/неделяградус/годградус/месяцградус/недельныйрадиан/годрадиан/месяцрадиан/ неделя Денежная единицаот манильи до полимера или вообще без валюты Обзор Угловая скорость в спорте Угловая скорость в оптическом накопителе Угловая скорость в космосе 70 90 оборотов в минуту при 2 оборотах потолочного вентилятора A0 90 оборотов за 2 5 90 об/мин Угловая скорость — это вектор, указывающий скорость вращения объекта вокруг оси. Угловая скорость в спорте Угловая скорость — полезное понятие в спорте. Например, знание и способность контролировать угловую, а также линейную скорость клюшки для гольфа, биты или ракетки во время замаха может помочь спортсмену улучшить свои результаты. Соотношение между угловой и линейной скоростью таково, что для удлиненного объекта, такого как клюшка для гольфа, точка, наиболее удаленная от оси вращения, имеет наибольшую линейную скорость, даже если угловая скорость одинакова в любой точке вдоль клюшки. Таким образом, используя более длинную клюшку, биту или ракетку, спортсмен может продвигать мяч с большей линейной скоростью, позволяя ему пройти большее расстояние, прежде чем он упадет. Мужчины были основными охотниками на первобытной охоте Спортсмены с более длинными конечностями могут развивать большую линейную скорость Более высокие люди с более длинными конечностями имеют преимущество, когда дело доходит до линейной скорости. Это преимущество может быть одной из причин, по которой мужчины были основными охотниками на первобытной охоте, а также почему люди стали выше ростом, потому что охота включает в себя метание камней и копий в добычу, а люди с более длинными конечностями могут развивать большую линейную скорость. Однако это может быть и недостатком. Людям с более длинными руками не только требуется дополнительная энергия, чтобы бросать предметы, но и более болезненно, когда люди с более длинными ногами ударяются о препятствие ногой по сравнению с более низкими людьми, которые двигают ногами с той же угловой скоростью. Угловая скорость важна в гимнастике, фигурном катании и прыжках в воду. Знание средней угловой скорости позволяет спортсменам рассчитать, сколько акробатических трюков они могут совершить до приземления или входа в воду. Чтобы выполнить больше вращений, таких как сальто, спортсмены максимально приближают ноги и руки к телу, чтобы минимизировать инерцию и максимизировать импульс, что приводит к увеличению угловой скорости. Чтобы приземлиться или войти в воду под правильным углом, спортсменам, возможно, придется уменьшить свою угловую скорость, слегка вытянув конечности, чтобы получить больший контроль над своими движениями. Метатели молота и диска также должны генерировать высокие угловые скорости, чтобы иметь возможность увеличить линейную скорость. Простой бросок молотка без его вращения на длинном шнуре генерирует гораздо меньшую скорость, чем если бы он сначала вращался. Многие спортсмены-олимпийцы вращают молоток три-четыре раза, прежде чем отпустить его, чтобы достичь максимально возможной линейной скорости. Угловая скорость в оптических накопителяхДиски в жестких дисках вращаются со скоростью от 4 200 об/мин в энергоэффективных портативных устройствах до 15 000 об/мин в высокопроизводительных серверах Угловая скорость используется для хранения данных на оптических носителях, таких как компакт-диски. И угловая, и линейная скорости используются для измерения скорости записи дисков и скорости дисководов. Разная скорость важна для разных режимов записи, и названия этих режимов часто относятся к скорости. Например, метод с постоянной линейной скоростью (CVL) был исходным режимом записи. В этом режиме данные записываются с одинаковой скоростью по всему диску. Зона постоянной линейной скорости (ZCLV) поддерживает постоянную линейную скорость в данной зоне диска, а не по всему диску. Диск обычно вращается медленнее при записи на его внешние области. Частичная постоянная угловая скорость (PCAV) — это метод записи постепенного увеличения угловой скорости до достижения определенного порога. Угловая скорость в космосеГеостационарная орбита Существует орбита, расположенная на расстоянии 35 786 километров (22 236 миль) от Земли; объект, следующий по этой орбите в том же направлении, что и вращение Земли, совершает его примерно за то же время, за которое Земля совершает оборот вокруг своей оси — один звездный день, что немногим меньше 24 часов. Таким образом, угловая скорость объектов на этой орбите равна угловой скорости Земли. Из-за этого эти объекты выглядят стационарными для наблюдателя на Земле. Эта орбита называется геостационарная орбита . Он используется для спутников, которые отслеживают изменения погоды и климата Земли (метеоспутники), изменения в океанах (геостационарные устройства цветного изображения океана или GOCI), а также спутники связи, используемые для вещания и связи. Спутниковые тарелки Спутники имеют определенное количество топлива, и как только они полностью его израсходуют, их больше нельзя использовать. Каталожные номера Статья написана Катериной Юрой Конвертер единиц. Редактировал и иллюстрировал Анатолий Золотков. Преобразователь площади Преобразователь плотности Преобразователь энергии и работы Преобразователь силы Преобразователь длины и расстояния Mass Converter Moment of Inertia Converter Moment of Force Converter Power Converter Pressure, Stress, Young’s Modulus Converter Specific Volume Converter Torque Converter Volume and Common Cooking Measurement Converter Dry Volume and Общие кулинарные измерения Конвертер линейной скорости и скорости Компактный калькулятор Полный калькулятор Определения единиц измерения У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут получите ответ от опытных технических переводчиков. Расчеты для преобразователя угловой скорости и частоты вращения выполнены с использованием математики с сайта unitconversion.org. |
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Направление этого вектора нормально к плоскости вращения и определяется по правилу правой руки. Он измеряется как отношение между изменением угла, под которым движется этот объект, называемым угловым смещением, и временем. Единицей угловой скорости в системе СИ является радиан в секунду.
И наоборот, использование более короткой ракетки или удерживание ее за рукоятку таким образом, что она укорачивается, позволяет спортсмену снизить линейную скорость.
Это связано с тем, что линейная скорость стопы на более длинной ноге будет выше.
Затем он остается постоянным для остальной части записи. Наконец, Постоянная угловая скорость (CAV) — это режим записи, который поддерживает постоянную угловую скорость во время записи. Это означает, что линейная скорость увеличивается по мере того, как пишущая головка перемещается к внешним областям диска. Этот метод также используется в жестких дисках и граммофонных пластинках.
Спутники связи также могут находиться на более низких или более высоких орбитах. Часто используются геостационарные орбиты, потому что антенны, направленные на спутник на этой орбите, не нужно было бы перенаправлять. Однако, если прямая видимость передатчика заблокирована, сигнал будет передаваться плохо, если вообще будет. Геостационарная орбита находится далеко, и в результате это вызывает задержку около 0,25 секунды. Для решения проблемы расстояния также необходимы более мощные передатчики. Исторически спутники связи использовались для дальней телефонной связи. Они были в значительной степени заменены морскими кросс-континентальными кабелями, проложенными по дну океана, но все еще используются в этом качестве для отдаленных районов. В последние 20 лет спутники связи также использовались для обеспечения подключения к Интернету в удаленных местах.
Обычно их выводят на другую орбиту, называемую орбитой захоронения или орбитой кладбища, которая намного выше геостационарной. Из-за этого в большинстве стран действуют правила, требующие от частных владельцев спутников подписать соглашение о том, что они переведут спутник на орбиту утилизации, как только он приблизится к концу своего жизненного цикла.
В технике часто используются более старые единицы, такие как оборота в минуту или оборота в секунду .
