Содержание
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями
- Подробности
- Просмотров: 803
«Физика — 10 класс»
Угловая скорость.
Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА1 > ВВ1 (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ.
Угол φ — угол между осью ОХ и радиус-вектором определяющим положение точки А (см. рис. 1.62).
Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы.
Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.
Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела υφ к промежутку времени υt, за который этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению
Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с.
Угловую скорость можно связать с частотой вращения.
Частота вращения — число полных оборотов за единицу времени (в СИ за 1 с).
Если тело совершает ν (греческая буква «ню») оборотов за 1 с, то время одного оборота равно 1/ν секунд.
Время, за которое тело совершает один полный оборот, называют периодом вращения и обозначают буквой Т.
Таким образом, связь между частотой и периодом вращения можно представить в виде
Полному обороту тела соответствует угол Δφ = 2π.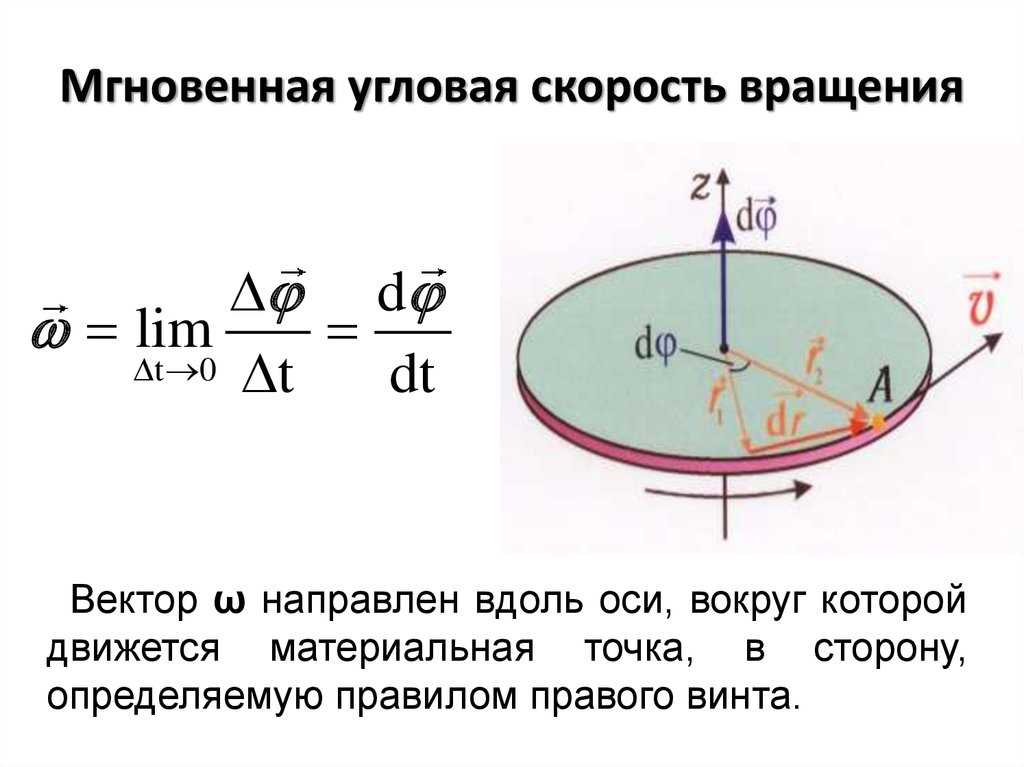 Поэтому согласно формуле (1.26)
Поэтому согласно формуле (1.26)
Если при равномерном вращении угловая скорость известна и в начальный момент времени t0 = 0 угол φ0 = 0, то угол поворота радиус-вектора за время t согласно уравнению (1.26)
φ = ωt.
Если φ0 ≠ 0, то φ — φ0 = ωt, или φ = φ0 ± ωt.
Радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности, 1 рад = 57°17’48». В радианной мере угол равен отношению длины дуги окружности к её радиусу: φ = l/R.
Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твёрдого тела, и осью ОХ увеличивается (рис. 1.63, а), и отрицательные, когда он уменьшается (рис. 1.63, б).
Тем самым мы можем найти положение точек вращающегося тела в любой момент времени.
Связь между линейной и угловой скоростями.
Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть её отличие от угловой скорости.
Мы уже отмечали, что при вращении абсолютно твёрдого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.
Установим связь между линейной скоростью любой точки вращающегося тела и его угловой скоростью. Точка, лежащая на окружности радиусом R, за один оборот пройдёт путь 2πR. Поскольку время одного оборота тела есть период Т, то модуль линейной скорости точки можно найти так:
Так как ω = 2πν, то
Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше её линейная скорость. Для точек земного экватора υ = 463 м/с, а для точек на широте Санкт-Петербурга υ = 233 м/с. На полюсах Земли υ = 0.
Модуль центростремительного ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:
Следовательно,
ацс = ω2R.
Запишем все возможные расчётные формулы для центростремительного ускорения:
Мы рассмотрели два простейших движения абсолютно твёрдого тела — поступательное и вращательное. Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.
Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.
На основании закона независимости движений можно описать сложное движение абсолютно твёрдого тела.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Следующая страница «Примеры решения задач по теме «Кинематика твёрдого тела»»
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Видеоурок: Движение по окружности
Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Движение по окружности
Траектория движения — окружность.
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.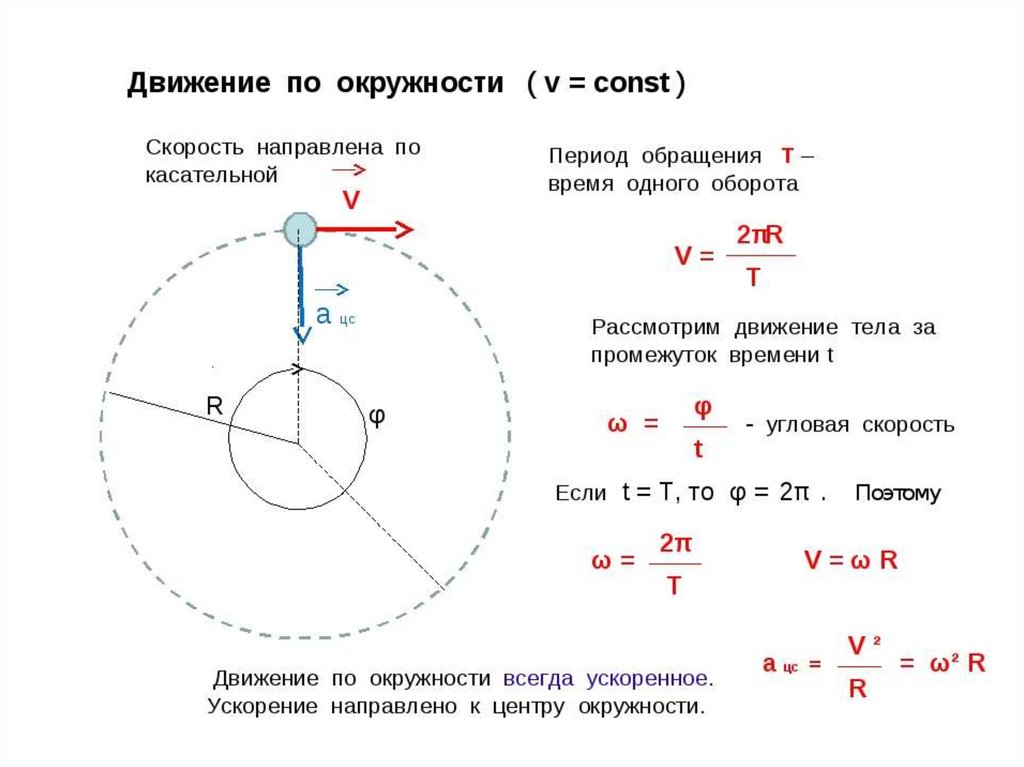
Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.
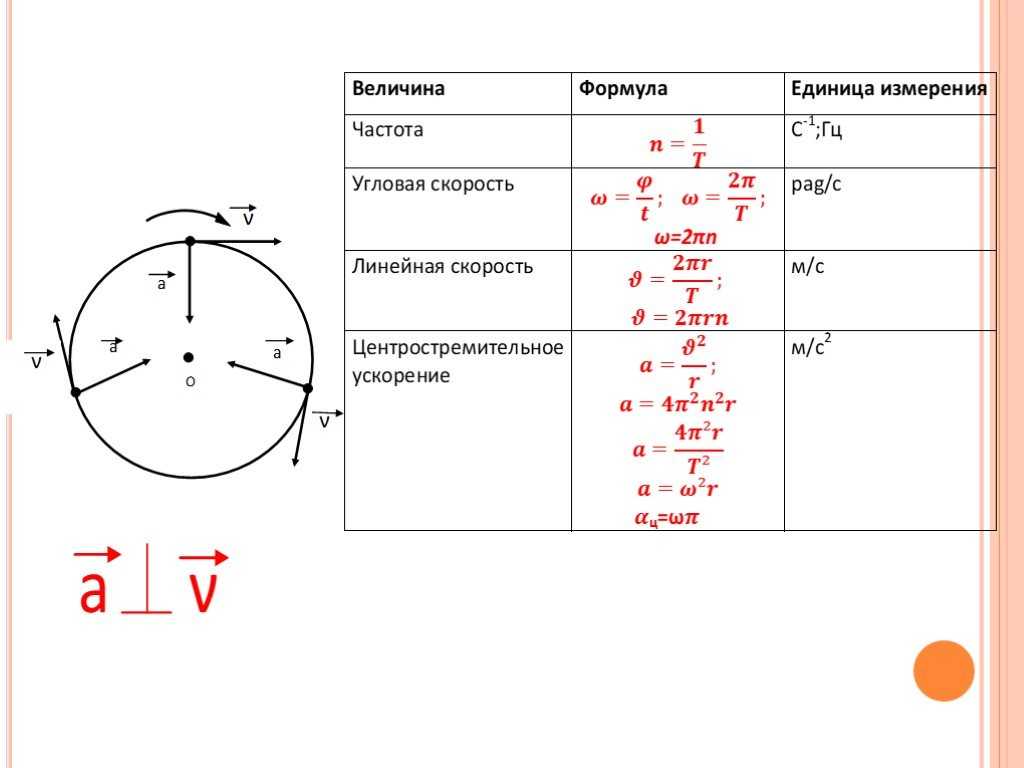
Основные характеристики движения
1. Линейная скорость
Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.
Так как траектория движения точки — окружность, то в качестве пути в числителе находится формула длины перемещения.
Поэтому формула мгновенной скорости приобретает следующий вид, где Т — период:
2. Центростремительное ускорение
Направлено перпендикулярно к линейной скорости на протяжении всего движения.
Центростремительное ускорение определяется по формуле:
3. Период вращения
Период вращения — это величина, определяющая время, за которое тело делает одно полное вращение.
Период — это скалярная величина. Основной единицей периода является [Т]=1с.
Период определяется по формуле:
где N — количество оборотов, t — время, за которое они были совершены.
4. Частота вращения
Определяет, насколько часто совершаются обороты в единицу времени.
Частота — скалярная величина. Измеряется в [n] = 1с-1.
Частота определяется по формуле:
5. Угловое перемещение
Угловое перемещение — величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.
Данная величина может измеряться в градусной или радианной мере углов.
6. Угловая скорость
Это значение, которое определяет, насколько изменяется угловое перемещение со временем.
Измеряется в 1 рад/с.
Определяется по формуле:
где
— угловая скорость материальной точки, 1/с
— угол поворота радиус — вектора, рад
— промежуток времени, с
Угловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:
-
2.
 1.3 «Просвещенный абсолютизм». Законодательное оформление сословного строя
1.3 «Просвещенный абсолютизм». Законодательное оформление сословного строя -
2.1.2 Северная война. Провозглашение Российской империи
-
1.4.6 Смута. Социальные движения в России в начале XVII в. Борьба с Речью Посполитой и со Швецией
-
1.2.1 Возникновение государственности у восточных славян. Князья и дружина. Вечевые порядки. Принятие христианства
-
1.3 Виды знаний
- Вконтакте
- Сайт
- расстояние — это длина пути тело следует при перемещении из одной точки в другую — перемещение есть расстояние по прямой между начальным и конечным положениями тела
- мы используем скорость и скорость как взаимозаменяемые, но имейте в виду, что скорость является мерой того, насколько быстро или медленно преодолевается расстояние, скорость, с которой преодолевается расстояние — скорость представляет собой вектор, определяющий, насколько быстро или медленно преодолевается расстояние и Направление
- Кинетическая энергия движущегося объекта
- Acceleration Unit Converter
- Радианы
- Кинетическая энергия вращающегося объекта
- Импульс
- Линейное смещение вдоль окружности
- Угловое смещение, образующее угол
Формулы движения — линейные и круглые
Линейные формулы движения
Средняя скорость / скорость движущегося объекта можно рассчитать как
V = S / T (1a)
, где
v = скорость или скорость (м/с, фут/с)
с = пройденное линейное расстояние (м, фут)
t = время (с)
Если ускорение является постоянным, то скорость может быть выражена как:
V = V 0 + A T (1B)
, где
v 0 = начальная линейная скорость (м/с, фут/с)
a = ускорение (м/с 2 , фут/с 2 )
Линейное расстояние может быть выражено как расстояние (Если ускорение постоянно):
S = V 0 T + 1/2 A T 2 (1C)
Комбинирование 1B и 1C для Express The Paint Velocity 1B и 1C .
V = (V 0 2 + 2 A S) 1/2 (1d)
Скорость может быть выражена как (скорость переменная)
V = DS / DT (1F)
Где
DS = изменение расстояния (M, FT)
DT = изменение во времени
Ускорение может быть выражено как
A = DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV / DV. dt (1 г)
, где
DV = изменение скорости (м/с, футов/с)
Пример — марафон, пробег
, если маратон — 42195 42195 MARAFON. — пробежал за 2:03:23 (7403 секунды) (Уилсон Кипсанг, Кения — 29 сентября 2013 г., Берлинский марафон) — среднюю скорость можно рассчитать
— пробежал за 2:03:23 (7403 секунды) (Уилсон Кипсанг, Кения — 29 сентября 2013 г., Берлинский марафон) — среднюю скорость можно рассчитать
v = (42195 м) / (7403 с)
= 5,7 м/с
= 20,5 км/ч
Пример. Ускорение автомобиля
Автомобиль разгоняется с 0 км/ч до 100 км/ч за 10 секунд. Ускорение можно рассчитать путем преобразования (1b) в
a = (v — v 0 ) / t
= ((100 км/ч) (1000 м/км) / (3600 с/ч) — (0 км/ч) ( 1000 м/км) / (3600 с/ч) ) / (10 с)
= 2,78 (м/с 2 )
Linear Motion Calculators
Average velocity
s — distance (m, km, ft, miles)
t — time used (s, h)
Расстояние
V 0 — Начальная скорость (м/с, фут/с)
A — Ускорение (м/с 2 , FT/S 2 )
T -S 2 )
T — -S 2 )
9004 T — -S 2 ) использованное время (с, ч)
Конечная скорость
v 0 — начальная скорость (м/с, фут/с)
а — ускорение (м/с 2 , фт/с 2 ) -1 90 м
90 90 , ft)
Ускорение
v — конечная скорость (м/с, фут/с)
v 0 — начальная скорость (м/с, фут/с)
время б/у
Круговое движение — вращение
Угловая скорость
Угловая скорость может быть выражена как (угловая скорость = постоянная):
ω = θ / t (2)
, где
ω = угловая скорость (рад / с)
θ = угловая скорость (рад / с)
θ = угловая скорость (рад / с)
ω = угловая скорость (рад / с)
ω = угловая скорость (рад / с)
ω = угловая скорость (рад / с)
ω = угловая скорость (рад / с) = угловое расстояние (RAD)
T = Время (S)
Угловая скорость и оборотная оборота:
ω = 2 π N / 60 (2A)
ω = 2 π N / 60 (2A)
ω = 2 π N / 60 (2A)0011
, где
n = обороты в минуту (об / мин)
π = 3,14 .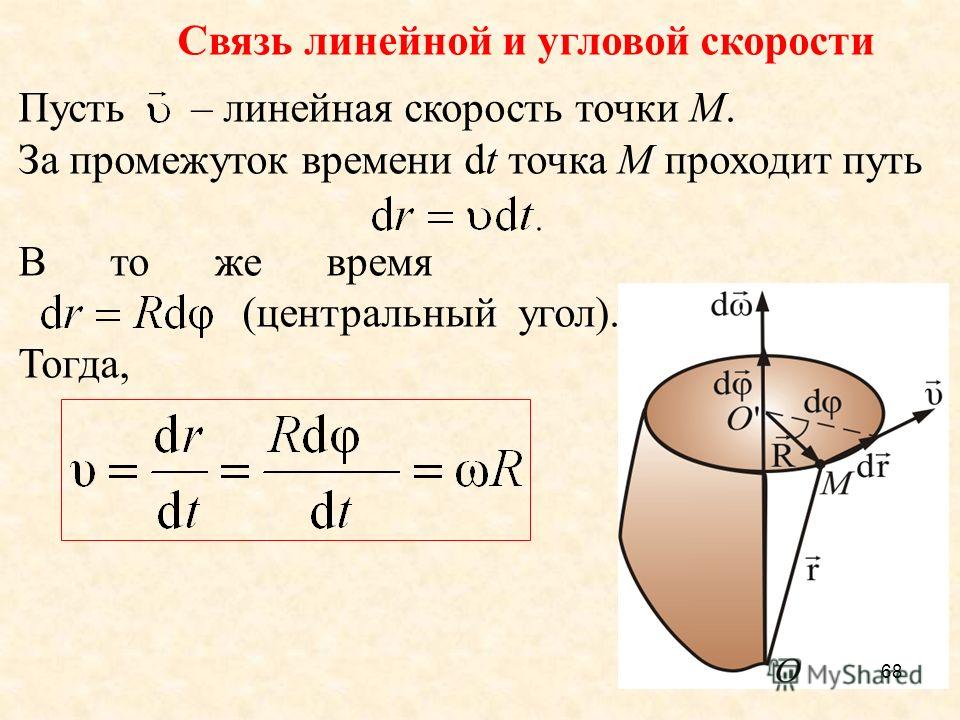 ..
..
Тангаенциальная скорость точки в угловой скорости — в Metric Or Imperial Units Like . M/S или футов/с — можно рассчитать как
V = ω R (2B)
, где
V = тангенциальная скорость (м/с, ft/s, in /с)
r = расстояние от центра до точки (м, футы, дюймы)
Пример – тангенциальная скорость велосипедной шины
A 26 дюймов велосипедное колесо вращается с угловой скоростью π радиан/с (0,5 оборота в секунду) . Тангенциальная скорость шины может быть рассчитана как
v = ( π радиан/с ) ((26 дюймов) / 2)
= 40,8 дюймов/с
Угловая скорость и ускорение.0141
Угловая скорость также может быть выражена как (угловое ускорение = постоянное):
ω = ω O + α T (2C)
, где
ω o = Англ. нулевой момент времени (рад/с)
α = угловое ускорение или замедление (рад/с 2 )
Угловое смещение
Угловое расстояние можно выразить как (угловое ускорение постоянно):
θ = ω O T + 1/2 α T 2 (2d)
Комбинирование 2A и 2C:
ω = (ω o
9 + ω = (ω o
9 ω = (ω O
ω = (ω O 9008
ω = (ω O и 2C:
ω = (ω O и 2C:
ω = (ω O и 2C:
.
2 α θ) 1/2
Angular Acceleration
Angular acceleration can be expressed as:
α = dω / dt = d 2 θ / dt 2 (2e)
, где
dθ = изменение углового расстояния (рад)
dt = изменение во времени (с)
или CC-BY-SA-3.0-2.5-2.0-1.0], через Wikimedia Commons
Маховик замедляется с 2000 об/мин ( оборотов /мин) до 1800 об/мин за 10 с . Замедление маховика можно рассчитать как
α = ((2000 Rev/Min ) — (1800 Rev/Min )) (0,01667 мин/с) (2 π RAD / Rev )/(10 с)
= 2,1 RAD /S 2
= (2,1 рад/с 2 ) (360/(2 π) градуары/рад)
= 120 градусов/S 2)
Угловой момент — или крутящий момент
Угловой момент или крутящий момент можно выразить как:
T = α I (2F)
, где
T = угловой момент или крутящий момент (N M)
I = момент инертных (LB M FT 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 9008 2 2 2 2 2 2 2 2 2 7 2 2 = момент инертных , кг·м 2 )
Теперь давайте посмотрим на подробное сравнение угловой скорости с линейной скоростью.
Когда предметы движутся в круговом направлении, можно увидеть линейную скорость и угловую скорость. Давайте разберемся в сравнении угловой скорости с линейной скоростью в деталях.
Угловая скорость против линейной скорости
Можно построить характеристики, связанные с движением по окружности, глядя на связь между дугой по окружности и радианным углом, который она образует. Прежде чем перейти к этим двум понятиям угловой скорости и линейной скорости, во-первых, нам нужно понять значение линейного смещения и углового смещения.
Изображение предоставлено: «Merry Go Round — Palace Pier, Брайтон» (CC BY 2.0) Марка Уорди
Мы уже знаем, что угловое смещение определяется как угол, на который движется частица при движении по кругу. Поскольку направление смещения параллельно оси, в этом случае угловое смещение представлено осевым вектором.
Смещения, испытываемые частицей при движении по окружности, делятся на две категории.
Они следующие:
Если радиус окружности равен r, то отношение между линейным смещением и угловым смещением можно представить следующим образом:
с =rθ или θ =s/r
Теперь линейная скорость определяется как скорость изменения линейного перемещения. Линейное смещение частицы может быть задано следующим образом:
И Когда речь идет о частицах, их угловая скорость определяется как скорость, с которой изменяется их угловое смещение.
∴ В простом смысле линейная скорость относится к скорости изменения длины дуги во времени, тогда как угловая скорость относится к скорости изменения угла вокруг центральной точки во времени.
Связь между угловой скоростью и линейной скоростью
Только что мы видели, что линейная скорость частицы задается как
И мы знаем, что s=r
r = радиус окружности постоянен Из уравнения угловой скорости мы знаем, что
Следовательно, отношение между линейной и угловой скоростью для тела, движущегося в равномерном круговом движении, определяется как:
Как указано в этом уравнении, линейная скорость (v) частицы прямо пропорциональна ее расстоянию от центра круговой траектории и угловой скорости частицы.
Сравнительный анализ угловой скорости и линейной скорости
Мы можем провести сравнение, основанное на нашем понимании терминов угловой скорости и линейной скорости, как показано в таблице ниже:
Угловая скорость Линейная скорость Угловая скорость частицы определяется как скорость изменения углового смещения. Линейная скорость определяется как скорость изменения линейного смещения. Угловая скорость частицы измеряется вдоль оси окружности. На протяжении всего кругового движения она остается постоянной. При круговом движении линейная скорость частицы соответствует окружности окружности. Она меняется в зависимости от положения точки на окружности. Угловая скорость обозначается символом Линейная скорость обозначается символом Формула: Формула: . Это связано с тем, что смещение частицы направлено в направлении центральной оси окружности.
Это векторная величина, что означает, что с ней связаны как величина, так и направление. Единицей измерения угловой скорости является градус и радиан. Где градус безразмерный, а радианы — единица СИ. Единицей измерения линейной скорости является м/с.
Часто задаваемые вопросы
В. Что такое скорость?
Ответ: Скорость, с которой что-либо движется или действует, называется его скоростью.
Слова скорость и скорость дают нам представление о том, насколько быстро или медленно перемещается предмет относительно нашего положения.
Мы сталкиваемся с ситуациями, когда нам нужно определить, какая из двух или более вещей движется быстрее, чем другая. Это случается очень часто.
Скорость объекта определяется как скорость изменения его положения относительно системы отсчета и во времени. Его можно измерить в метрах в секунду (мс-1).
Когда скорость тела изменяется на значительную величину или в определенном направлении, говорят, что тело ускоряется.
В. Что вы подразумеваете под угловой скоростью? Приведите примеры.
Ответ: Это скорость вращения частицы вокруг центральной точки.
Угловая скорость частицы определяется как скорость изменения углового смещения частицы. Угловая скорость частицы направлена вдоль оси круга, когда предмет движется по кругу. Другими словами, угловая скорость является постоянной величиной и обозначается «ω».
Примерами угловой скорости являются колесо обозрения, Земля, Автобусное колесо и Вентилятор.
В. Что вы подразумеваете под линейной скоростью? Приведите примеры.
Ответ: По сути, это скорость, с которой частица движется по прямой траектории.
Линейная скорость может быть определена как скорость изменения линейного перемещения во времени. Угловая и линейная скорости присутствуют во всем, что вращается или движется по окружности.
Например, покатайтесь на карусели. Камень, брошенный с края вращающейся карусели, не упадет прямо вниз. Вместо этого он будет продолжать двигаться вперед с той же скоростью, с которой двигалась карусель, когда был брошен камень. Это линейная скорость камня.
В. Если объект проходит расстояние 5 метров за 2 секунды. Тогда какова будет линейная скорость этого объекта?
Ответ: Линейную скорость можно рассчитать по простой формуле.
Дано: смещение = 5 метров, время = 2 секунды
Линейная скорость: = S/T
∴ = 510005944444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444454454454445444444444544459нте.
2,5 м/с
∴ Линейная скорость объекта 2,5 м/с
Q. Угловая скорость и угловая скорость идентичны?
Ответ: Обе величины имеют сходства и различия.
Сходства между ними в том, что их единицей измерения является радиан в секунду. Пока они различаются скалярным и векторным аспектом. Угловая скорость () является скалярной величиной, тогда как угловая скорость () является векторной величиной.
В. Линейная скорость и линейная скорость идентичны?
Ответ: Хотя и скорость, и скорость предназначены для определения расстояния до движущегося объекта, они в чем-то различаются.
Во-первых, скорость является скалярной величиной. Таким образом, выражение скорости в м/с просто показывает величину. Он ничего не говорит о движении объекта. Однако линейная скорость описывает направление, в котором что-то движется.
 1.3 «Просвещенный абсолютизм». Законодательное оформление сословного строя
1.3 «Просвещенный абсолютизм». Законодательное оформление сословного строя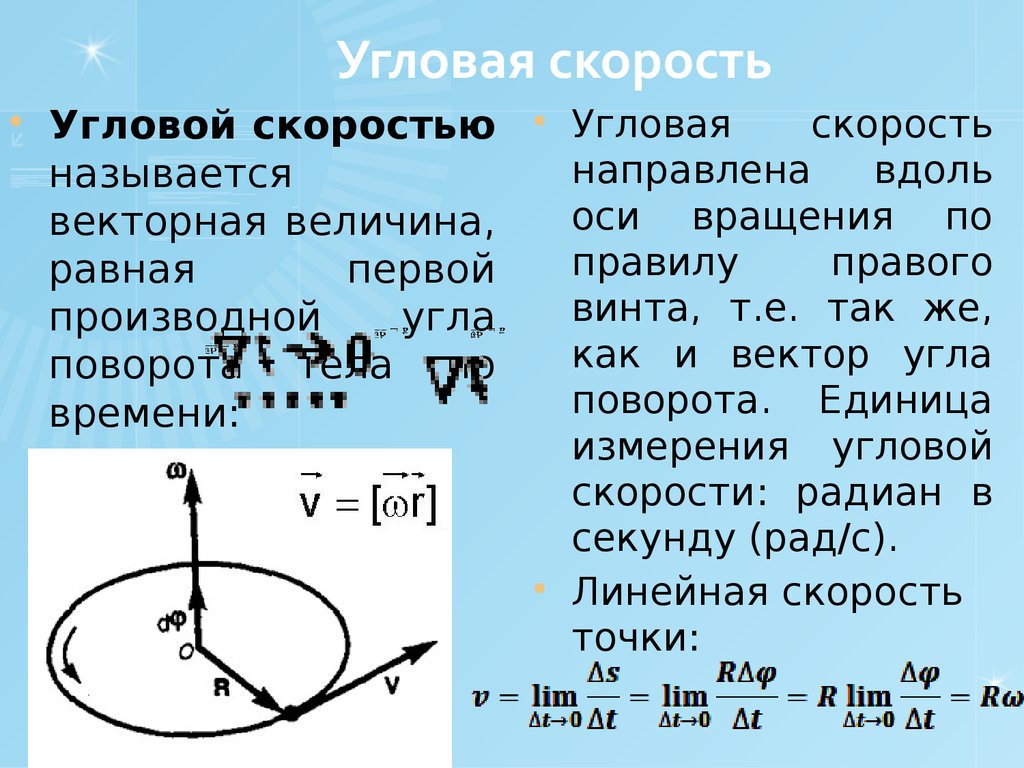 2 α θ) 1/2
2 α θ) 1/2
 Они следующие:
Они следующие: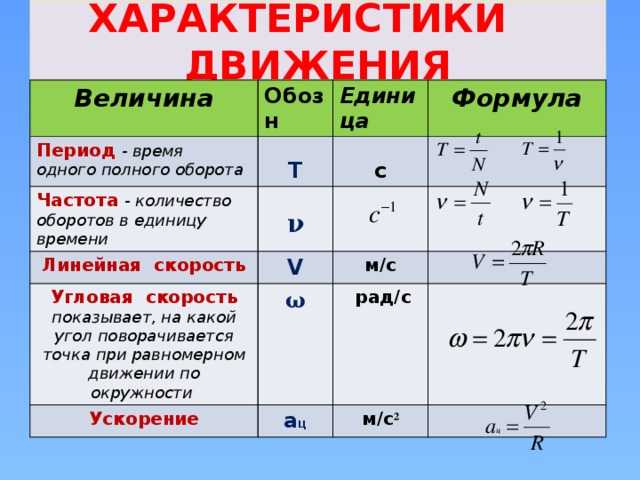
 Это связано с тем, что смещение частицы направлено в направлении центральной оси окружности.
Это связано с тем, что смещение частицы направлено в направлении центральной оси окружности.
 Скорость объекта определяется как скорость изменения его положения относительно системы отсчета и во времени. Его можно измерить в метрах в секунду (мс-1).
Скорость объекта определяется как скорость изменения его положения относительно системы отсчета и во времени. Его можно измерить в метрах в секунду (мс-1).
 2,5 м/с
2,5 м/с 