Содержание
5 ответов, которые вы должны знать
Движение объекта по круговой траектории относительно его неподвижной оси известно как вращательное движение. Эта статья о скорости, создаваемой этим движением.
Чтобы узнать, как найти угловую скорость, я сначала узнаю об этом. Когда тело движется по круговой траектории, скорость, которая возникает из-за этого движения, называется угловой скоростью. Примеры угловой скорости колеса, карусель и многое другое.
Все мы знаем о скорости поступательного движения, вызванной линейным движением объекта. Но когда тело вращается или движется по круговой траектории, помимо линейной скорости, существует еще и угловая скорость. Эта скорость говорит нам о векторной скорости изменения угла движущегося тела. Он дает представление о том, насколько быстро вращается или вращается тело. В физике скорость вращения также обозначает угловую скорость.
Изображение Фото: DNET на основе растровой версии, выпущенной под GFDL, Угловая скорость, CC BY-SA 3. 0
0
Орбитальная угловая скорость и угловая скорость вращения — это два вида угловой скорости. Орбитальная угловая скорость определяет скорость изменения угла объекта относительно фиксированной точки. В то же время угловая скорость вращения определяет скорость вращения объекта относительно его центра вращения.
Как найти угловую скорость из линейной скорости
Мы знаем, что угловая скорость определяется как скорость изменения угла движущегося тела. Итак, у нас есть:
[латекс] \ omega = \ frac {\ Delta \ theta } {\ Delta t} = \ frac {\ mathrm {d} \ theta} {\ mathrm {d} t} [/latex]
Из рисунка выше видно, что частица перемещается из точки A в точку B. Здесь расстояние, пройденное частицей, s, равно длине дуги кругового пути.
По формуле:
[latex]Дуга = радиус \умножить на угол[/latex]
[латекс]s = \тета\cdot r[/латекс]
дифференцируя обе части по t
[латекс] \ frac {\ mathrm {d} s} {\ mathrm {d} t} = r \ cdot \ frac {\ mathrm {d} \ theta} {\ mathrm {d} t} [/latex]
Мы знаем, что дифференцирование смещения дает нам линейную скорость, а дифференцирование угла дает угловую скорость.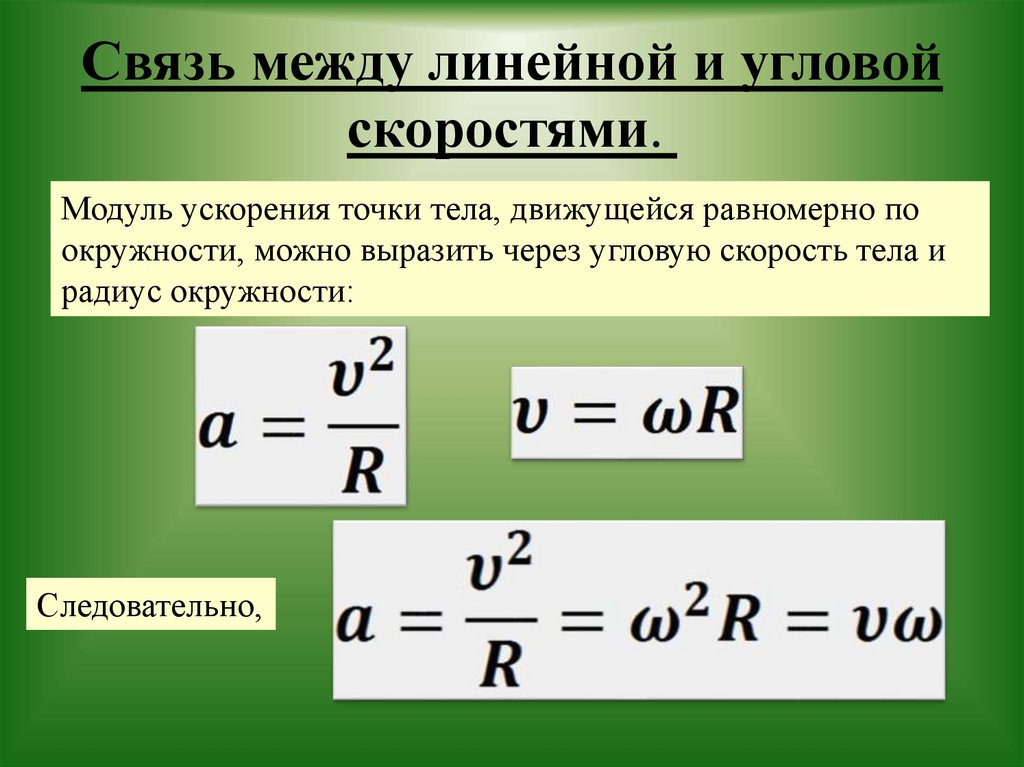 {-1}[/латекс]
{-1}[/латекс]
Как найти угловую скорость в радианах в секунду
Во вращательной кинематике частица движется по круговой траектории. Угловая скорость определяет, насколько быстро объект движется. Следовательно, вычислив количество оборотов, совершаемых объектом за заданное время, мы можем узнать его скорость.
[латекс]\омега = \фрак{революций}{время}[/латекс]
Мы знаем, что для круговой траектории 1 полный оборот составляет 360 °. А 360 ° равняется 2π в радианах. Принимая время в стандартной единице, единица омеги становится;
[латекс]\омега = \фракция{радианы}{секунды}[/латекс]
Предположим, прялка совершает 4830 оборотов в минуту. Тогда угловая скорость в радианах в секунду будет:
[латекс]\omega = \frac{4830 об.}{1 мин}[/латекс]
1 оборот = 2π радиан
4830 оборот = 4830 × 2π
и 1 мин. = 60 секунд
Следовательно:
[латекс]\омега = \фрак{4830 \cdot 2\Pi }{60}[/латекс]
[латекс]\омега = 161 рад \cdot s^{-1}[/латекс]
Как найти угловую скорость с массой и радиусом
Так же, как для поступательного движения существует линейный импульс, аналогично для вращательного движения объекта существует угловой момент L.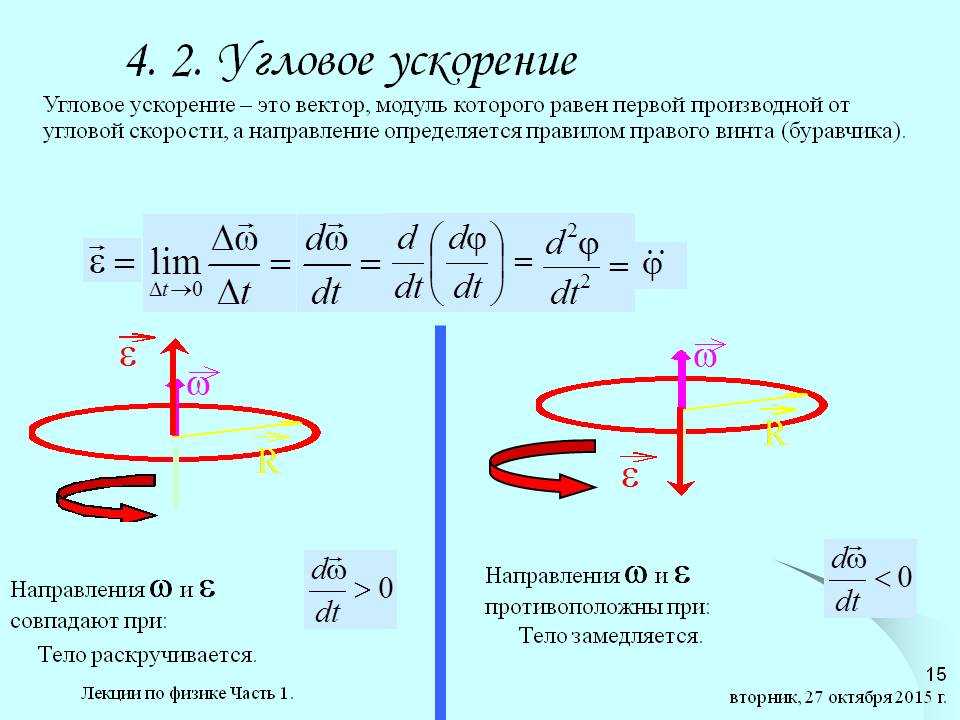 {-1}[/латекс]
{-1}[/латекс]
Часто задаваемые вопросы (FAQ)
Что такое вращательное движение?
Движение можно разделить на несколько типов, одним из которых является вращательное движение.
Когда тело движется по круговой траектории вокруг фиксированной точки, говорят, что оно находится во вращательном движении. Частицы вращающегося тела движутся в одной фазе с одинаковой угловой скоростью — например, движение электрона вокруг ядра.
Определить угловую скорость?
Когда частица движется по круговой траектории, она вместе с линейной скоростью достигает угловой скорости.
Скорость изменения угла вращающегося объекта называется его угловой скоростью. Это аналог линейной скорости поступательного движения. Он определяет, насколько быстро объект вращается.
Приведите пример угловой скорости из повседневной жизни.
Колесо обозрения — основной пример угловой скорости из нашей повседневной жизни. {-1}[/латекс]
{-1}[/латекс]
С КАКОЙ СКОРОСТЬЮ ВРАЩАЕТСЯ ЗЕМЛЯ?
С какой скоростью вращается Земля вокруг своей оси? Не для кого не секрет, что смена дня и ночи технически вызвана вращением Земли. Но вам когда-нибудь приходило в голову с какой скоростью она вращается? И как посчитать эту скорость?
Если говорить о равномерном движении по окружности, можно выделить две скорости: угловую (ω) и линейную (v). Давайте найдем и ту, и другую для нашей прекрасной голубой планеты.
Угловая скорость вращения Земли
Угловая скорость определяет то, как быстро изменяется угол с течением в времени. Так как один полный оборот соответствует углу в 360о или 2π, а время, за которое он совершается есть период Т, то угловую скорость можно выразить как:
На всякий случай. Чтобы не было вопросов откуда берется 2π.
Один радиан соответствует углу с дугою равной радиусу. Соответственно чтобы посчитать количество радиан в окружности нам необходимо ее длину то есть 2πR, поделить на радиус R. R и R сокращаем и получаем 2π. Или приближенно 6.28.
R и R сокращаем и получаем 2π. Или приближенно 6.28.
Мы знаем, что в сутках 24 часа, а, следовательно, можно предположить, что период обращения Земли вокруг своей оси Т составит так же 24 часа. Но не торопитесь переводить это время в секунды и подставлять в уравнение, записанное выше. Так как Земля вращается еще вокруг солнца, то период обращения её вокруг собственной оси будет немного короче привычных нам солнечных суток и составит 23 часа 56 минут и 4 секунды. Это так называемые звездные сутки. В пересчете на секунды мы получаем: Т=86164 с.
Теперь можно найти угловую скорость:
Линейная скорость вращения Земли
Если говорить об угловой скорости, то она одинакова для любой точки нашей планеты. И не важно: пингвин в Антарктике, слон в Африке или Вы у себя дома, все будут иметь одинаковую угловую скорость. Но когда речь заходит о скорости линейной, то тут все наоборот. Она будет максимальна на экваторе и убывать к полюсам, так как напрямую зависит от радиуса окружности вращения. А это значит, что если вы залезете на табуретку вкрутить лампочку, то ваша линейная скорость увеличится. Строго говоря, линейная скорость описывает скорее не вращение Земли вокруг своей оси, она описывает вращение каких то отдельных её точек.
А это значит, что если вы залезете на табуретку вкрутить лампочку, то ваша линейная скорость увеличится. Строго говоря, линейная скорость описывает скорее не вращение Земли вокруг своей оси, она описывает вращение каких то отдельных её точек.
Рассчитать линейную скорость очень просто. По определению, скорость — это отношение пройденного пути ко времени, за которое этот путь был совершен. Если за один оборот мы проходим путь, равный длине окружности, а время движения будет ни что иное как период обращения Т, то, выразив длину окружности из известной школьной формулы: L= 2πR, мы получим уравнение для расчета линейной скорости:
Так как угловая скорость , то мы можем смело записать:
Радиус земли на экваторе R = 6378245 м, а значит линейная скорость там будет равна: м/с.
Для сравнения скорость звука в воздухе составляет 365 м/с. А это значит, что, сидя спокойно на стульчике где-нибудь в Африке или Индонезии мы будем двигаться со скоростями, превышающими звук. Если перевести эту величину в километры в час, то получится 1674 км/ч!!! В общем скорости сопоставимые со скоростями сверхзвуковой авиации.
Если перевести эту величину в километры в час, то получится 1674 км/ч!!! В общем скорости сопоставимые со скоростями сверхзвуковой авиации.
Линейная скорость в зависимости от широты
Но это на экваторе. Ближе к полюсам, как я уже говорил, значение будет ниже. Так как радиус вращения будет снижаться.
Для того чтоб найти радиус вращения на той или иной широте. Необходимо косинус этой широты умножить на земной радиус.
К примеру, для Санкт-Петербурга соответствует шестидесятая северная широта. Косинус шестидесяти градусов как известно одна вторая. То есть радиус вращения будет вдвое меньше земного, а значит и линейная скорость будет так же в два раза меньше экваториальной, всего 837 км/ч.
А с какой линейной скоростью вращаетесь Вы??? Ответы можете писать в комментариях, а я с Вами прощаюсь. Всего хорошего, до скорых встреч.
Обороты и угловая скорость
поворот вектора на — это изменение, которое только
изменяет направление, а не длину вектора. А
А
вращение состоит из оси вращения и
скорость вращения . Принимая ось вращения за
направление и скорость вращения как длину, мы можем написать
вращение как вектор, известное как угловая скорость
вектор \(\vec{\omega}\). Мы используем
9\circ/s$.
Ось вращения:
$\шляпа\имат$
$\шляпа\jmath$
$\шляпа{к}$
$\шляпа\имат + \шляпа\jmath$
$\шляпа\imath + \шляпа\jmath + \шляпа{k}$
Вектор угловой скорости $\vec\omega$. Направление
$\vec\omega$ — ось вращения, а величина
— скорость вращения (положительное направление, заданное
правило правой руки).
Векторные производные и повороты
Если единичный вектор \(\hat{a}\) вращается, то угловой
вектор скорости \(\vec{\omega}\) определяется так, что:
\[\dot{\шляпа{а}} = \vec{\omega} \times \шляпа{а}\]
\[\ начало {выровнено}
\ точка {\ vec {а}} = \ нижняя скобка {\ точка {а}
\шляпа{а}}_{\operatorname{Proj}(\dot{\vec{a}}, \vec{a})} +
\ underbrace{\ vec {\ omega} \ раз
\vec{a}}_{\operatorname{Comp}(\dot{\vec{a}}, \vec{a})}
\конец{выровнено}\]
Используя тот же подход, что и #rvc-em, мы пишем $\vec{a} =
a\hat{a}$, продифференцируйте это и используйте rkr-ew, чтобы найти:
\[\ начало {выровнено}
\dot{\vec{a}} &= \frac{d}{dt} \big( a \hat{a} \big) \\
&= \точка{а} \шляпа{а} + а \точка{\шляпа{а}} \\
&= \dot{a} \hat{a} + a (\vec\omega \times \hat{a}) \\
&= \dot{a} \hat{a} + \vec\omega \times (a \hat{a}) \\
&= \dot{a} \hat{a} + \vec\omega \times \vec{a}.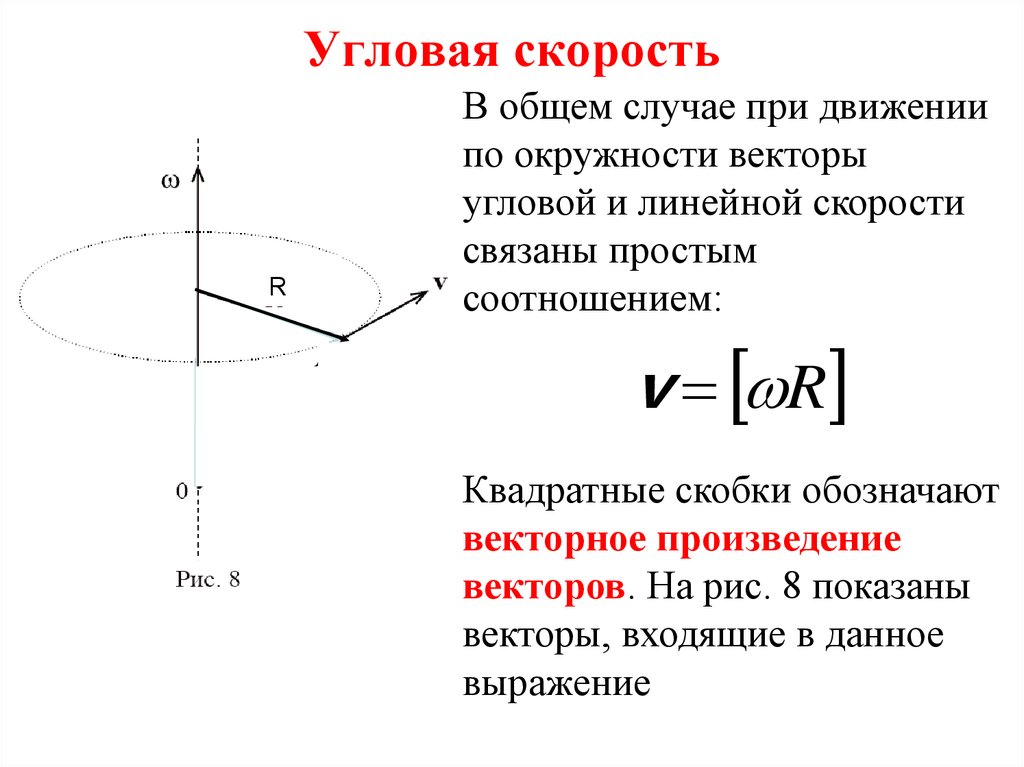
\конец{выровнено}\]
Сравнивая это с #rvc-em
показывает, что двумя компонентами являются проекция и
дополнительная проекция соответственно.
\[\dot{\vec{a}} = \vec{\omega} \times \vec{a}
\qquad\text{если $\vec{a}$ имеет постоянную длину}\]
Это видно из того, что $\dot{a} = 0$, если $a$
константа (вектор фиксированной длины), подставленная в #rkr-ed.
Вращения в 2D
В 2D угловую скорость можно рассматривать как скаляр
(положительный для против часовой стрелки, отрицательный для по часовой стрелке).
Этот скаляр является просто внеплоскостной составляющей
полный вектор угловой скорости. Мы можем нарисовать угловой
скорость как вектор, указывающий из плоскости, или
как круг-стрелка в плоскости, что проще для 2D
диаграммы.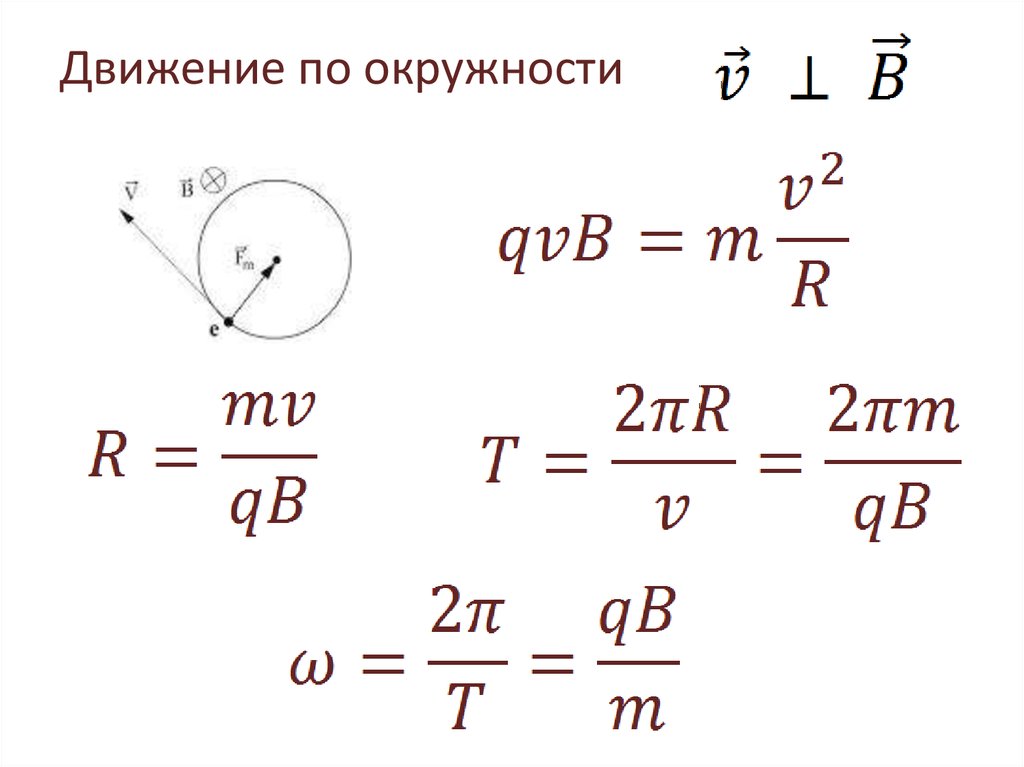
Показать:
Сравнение векторного и скалярного представлений
$\vec\omega$ для двумерных вращений.
В 2D скаляр угловой скорости $\omega$ — это просто
производная угла поворота $\theta$ в плоскости:
\[\омега = \точка\тета\]
Возьмем $\hat{a}$ единичный вектор, вращающийся в двумерном пространстве.
$\hat\imath$ – плоскость $\hat\jmath$, образующая угол
$\theta$ с осью $x$, как на рисунке #rkr-f2. Затем:
\[\ шляпа {а} = \ соз \ тета \, \ шляпа \ имат
+ \sin\theta\,\hat\jmath.\]
Дифференцирование этого выражения дает:
\[\dot{\hat{a}} = -\sin\theta \, \dot\theta \,\hat\imath
+ \cos\theta\,\dot\theta\,\hat\jmath.\]
Теперь рассмотрим вектор угловой скорости
$\vec\омега$. Поскольку вращение находится в
$\hat\imath$–плоскость $\hat\jmath$, угловая скорость
вектор должен быть в направлении $\hat{k}$. Таким образом
Таким образом
$\vec\omega = \omega \hat{k}$. Теперь мы можем вычислить
производная от $\hat{a}$ с использованием #rkr-ew, что дает:
\[\ начало {выровнено}
\dot{\шляпа{а}} &= \vec\omega \times \шляпа{а} \\
&= \omega\hat{k} \times \big( \cos\theta \,\hat\imath
+ \sin\theta\,\hat\jmath\big) \\
&= \omega \cos\theta\,(\hat{k} \times\hat\imath)
+ \omega \sin\theta\,(\hat{k} \times \hat\jmath) \\
&= \omega \cos\theta \,\hat\jmath
+ \omega \sin\theta\,(-\hat\imath) \\
&= — \omega \sin\theta \,\hat\imath
+ \omega \cos\theta\,\hat\jmath.
\конец{выровнено}\]
Сравнивая это выражение с предыдущим для
$\dot{\hat{a}}$ мы видим, что $\omega = \dot\theta$.
Правило правой руки для угловых скоростей означает
что вращения против часовой стрелки положительны, как и
обычное соглашение о направлении угла.
Повороты и векторные «позиции»
Тот факт, что векторы не имеют
position означает, что поворот вектора не зависит от
где нарисованы векторы, как и для производных.
Показать:
Вращательное движение векторов, которые нарисованы движущимися
о. Обратите внимание, что нарисованная позиция не влияет на
угловая скорость $\omega$ или производные векторы.
Свойства вращения
Вращения — это жестких преобразования , что означает, что
они сохраняют постоянными все длины векторов и все относительные
векторные углы. Эти факты отражены в следующем
результаты, все из которых рассматривают два вектора $\vec{a}$ и
$\vec{b}$, вращающиеся с угловой скоростью
$\vec\омега$.
\[\точка{\vec{а}} \cdot \vec{а} = 0\]
Использование #rkr-el и скаляра
формула тройного продукта #rvi-es дает:
\[\ начало {выровнено}
\vec{a} \cdot \dot{\vec{a}}
&= \vec{a} \cdot \big( \vec{\omega} \times \vec{a} \big) \\
&= \vec{\omega} \cdot \big( \vec{a} \times \vec{a} \big) \\
&= 0. {-1}\left(\frac{\vec{b} \cdot
{-1}\left(\frac{\vec{b} \cdot
\vec{a}}{b a}\right) = \text{константа}\]
Сначала рассмотрим скалярное произведение $\vec{a} \cdot
\vec{b}$ и показать, что это не меняется с
время. Мы делаем это, используя скалярное тройное произведение
формула #rvi-es для нахождения:
\[\ начало {выровнено}
\frac{d}{dt} \big( \vec{a} \cdot \vec{b} \big)
&= \dot{\vec{a}} \cdot \vec{b} + \vec{a} \cdot \dot{\vec{b}} \\
&= (\vec{\omega} \times \vec{a}) \cdot \vec{b} + \vec{a} \cdot (\vec{\omega} \times \vec{b}) \\
&= \vec{b} \cdot (\vec{\omega} \times \vec{a}) + \vec{b} \cdot (\vec{a} \times \vec{\omega}) \\
&= \vec{b} \cdot (\vec{\omega} \times \vec{a}) — \vec{b} \cdot (\vec{\omega} \times \vec{a}) \\
&= 0.
\конец{выровнено}\]
Теперь $\vec{a} \cdot \vec{b}$ постоянна и длины
$a$ и $b$ постоянны, поэтому угол $\theta$ между
векторы должны быть постоянными.
\[\dot{\vec{a}} = 0 \qquad \text{если $\vec{a}$ вращается и параллельно $\vec\omega$}\]
Из #rkr-el мы знаем, что
производная
\[\dot{\vec{a}} = \vec\omega \times \vec{a},\]
но векторное произведение равно нулю для параллельных векторов, поэтому
эта производная равна нулю.
Формула вращения Родригеса
Формула вращения Родригеса дает явную формулу для
вектор, повернутый на угол вокруг заданной оси.
\[\operatorname{Rot}(\vec{a}; \theta, \hat{b}) =
\vec{a} \cos\theta + (\hat{b} \times
\vec{a}) \sin\theta + \шляпа{b} (\шляпа{b} \cdot
\vec{a}) (1 — \cos\theta)\]
Предположим, что \(\vec{a}\) не параллелен
\(\шляпа{б}\). Тогда пусть \(\vec{v} = \hat{b} \times
\vec{a}\) и \(\vec{u} = \vec{v}
\times \vec{b}\), поэтому \(\hat{u}, \hat{v}, \hat{b}\)
является правым ортонормированным базисом.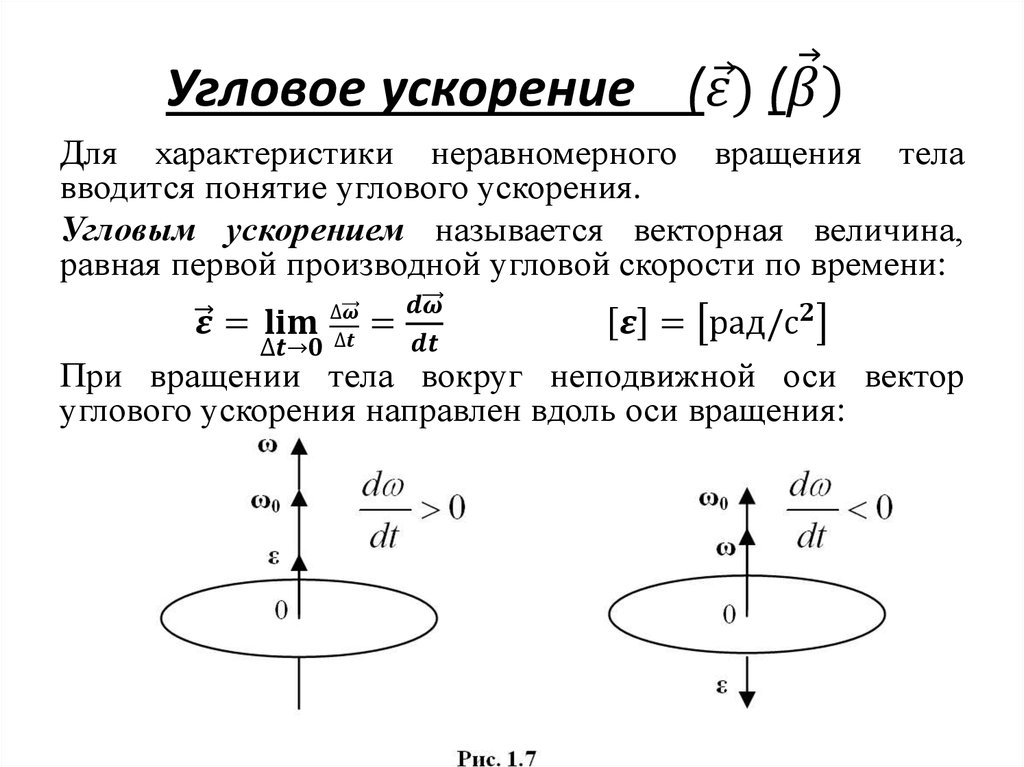 Брать
Брать
\(\phi\) угол между \(\vec{a}\) и
\(\шляпа{б}\). Затем мы делаем поворот на \(\theta\) в
плоскость \(\шляпа{u}\)-\(\шляпа{v}\):
\[\begin{выровнено} \vec{a} &= a \sin\phi
\,\шляпа{и} + а\cos\phi\,\шляпа{b} \\
\operatorname{Rot}(\vec{a};\theta,\hat{b}) &= a
\cos\theta\sin\phi\,\hat{u} + a\sin\theta\sin\phi
\,\шляпа{v} + a \cos\phi \,\шляпа{b}.\end{выровнено}\]
Теперь мы хотим преобразовать из
\(\шляпа{u},\шляпа{v},\шляпа{b}\) для записи повернутого
результат в терминах \(\vec{a}, (\hat{b} \times
\vec{a}), \шляпа{b}\). Для этого нам нужно работать
что такое \(\шляпа{u},\шляпа{v},\шляпа{b}\) с точки зрения
эти другие векторы.
\[\begin{align} \шляпа{v} &= \frac{\шляпа{b} \times
\vec{a}}{\|\шляпа{b} \times \vec{a}\|} =
\frac{\hat{b} \times \vec{a}}{a \sin\phi} \\
\шляпа{u} &= \frac{\vec{v} \times
\шляпа{b}}{\|\vec{v} \times \vec{b}\|} =
\ frac {\ vec {v} \ times \ hat {b}} {a \ sin \ phi} =
\frac{(\шляпа{b} \times \vec{a}) \times \шляпа{b}}{a
\sin\phi} = \frac{\hat{b} \times (\vec{a} \times
\шляпа{b})}{а \sin\phi} \\
&= \frac{\vec{a} — (\шляпа{b}
\cdot \vec{a}) \hat{b}}{a \sin\phi} = \frac{1}{a
\sin\phi} \vec{a} — \frac{\hat{b} \cdot
\vec{a}}{a \sin\phi} \hat{b}. \end{aligned}\]
\end{aligned}\]
Подставляя их в повернутое векторное выражение
выше дает
\[\ начало {выровнено}
\operatorname{Rot}(\vec{a};\theta,\hat{b}) &= a
\cos\theta \sin\phi \, \left( \frac{1}{a \sin\phi}
\vec{a} — \frac{\hat{b} \cdot \vec{a}}{a
\sin\phi} \шляпа{b} \право) \\
& \qquad + a \sin\theta \sin\phi \, \left(
\ frac{\ hat {b} \ times \ vec {a}} {a \ sin \ phi} \ right)
+ a \cos\phi\,\hat{b} \\ &= \cos\theta
\,\vec{a} — \cos\theta \,(\hat{b} \cdot
\vec{a}) \,\шляпа{b} + \sin\theta \,(\шляпа{b} \times
\vec{a}) + a\cos\theta \,\hat{b} \\ &=
\cos\theta \,\vec{a} + (1 — \cos\theta) (\hat{b}
\cdot \vec{a}) \,\шляпа{b} + \sin\theta \,(\шляпа{b}
\times \vec{a}).\end{выровнено}\]
Угловое смещение, скорость, ускорение
|
Мы живем в мире, который определяется тремя пространственными измерениями и одним На этой странице мы будем рассматривать только вращение твердого тела вокруг Поскольку объект вращается вокруг оси вращения , самый простой способ фи = тета 1 — тета 0 Угловое смещение – это Угловое смещение измеряется в единицах радиан . Два пи радиана равны для углового смещения фи , с = фи * г р > рб са > сб Угловая скорость — омега объекта омега = (тета 1 — тета 0) / (t1 — t0) Это средняя угловая скорость за интервал времени от t0 до t1 , омега = d тета / dt где символ д/дт — дифференциал от исчисления. Угловая скорость измеряется в радиан в секунду , или для углового смещения фи , V = омега * г р > рб Ва > Вб Когда мы изначально Среднее угловое ускорение — альфа объекта альфа = (омега 1 — омега 0) / (t1 — t0) Как и в случае с угловой скоростью, это только среднее значение угловой скорости. альфа = d омега / dt Точно так же, как |
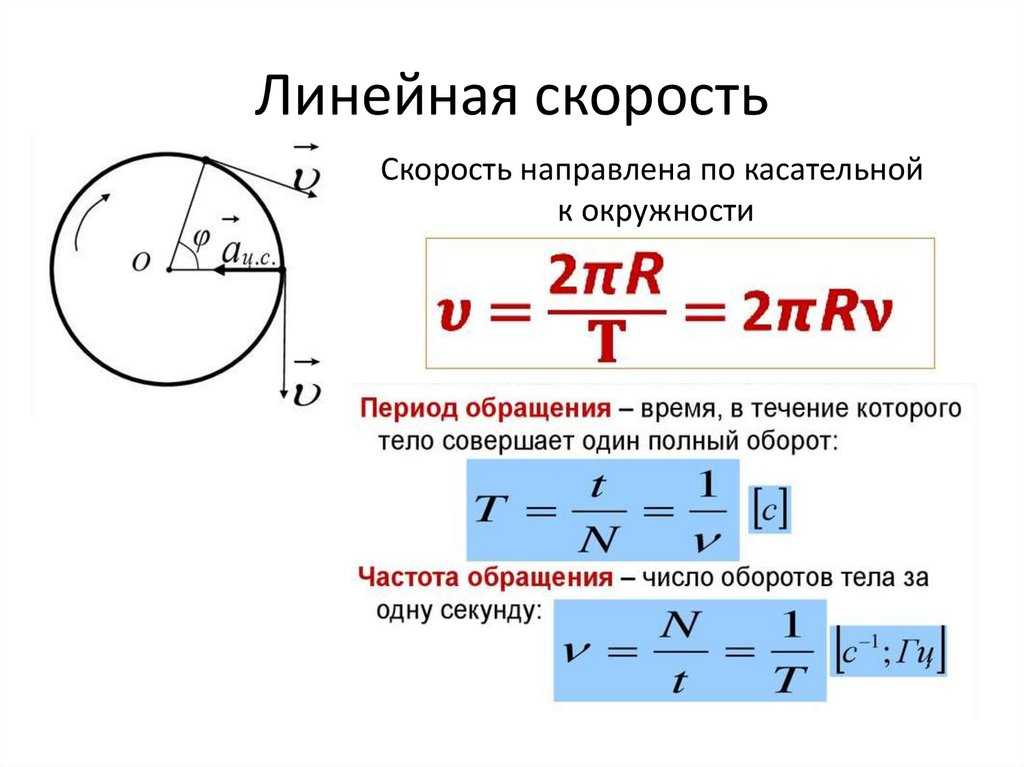 Объекты перемещаются внутри этой области двумя способами.
Объекты перемещаются внутри этой области двумя способами.
 Направление важно
Направление важно Как объект
Как объект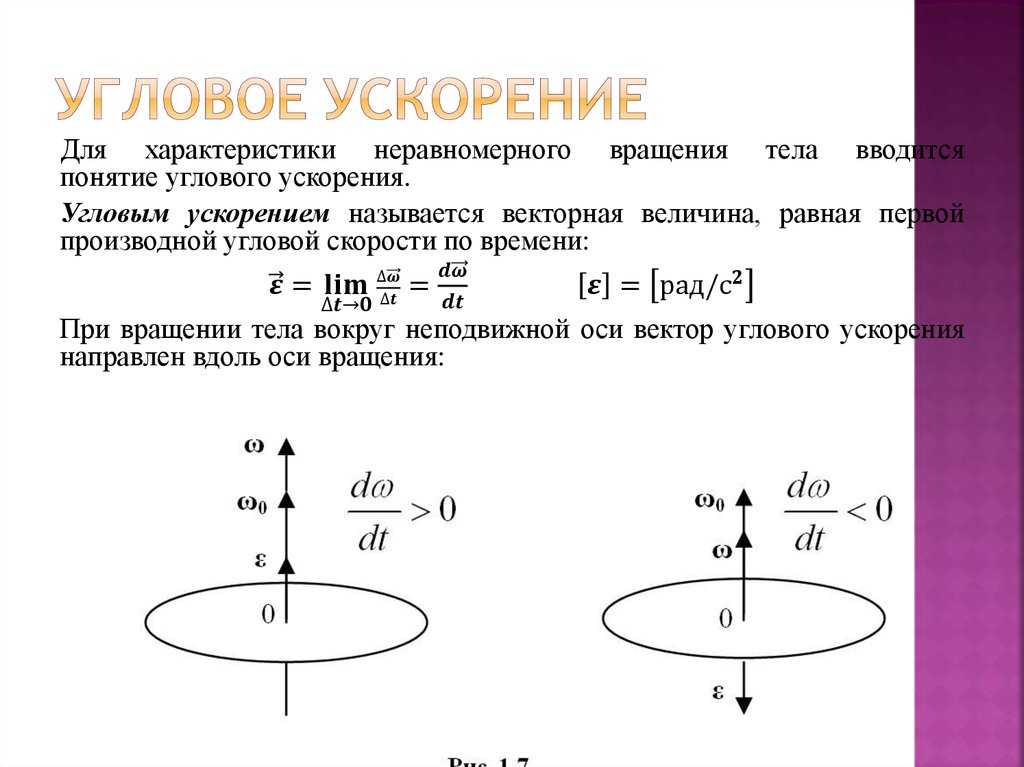 Если мы сократим
Если мы сократим Тангенциальная скорость V равна угловой
Тангенциальная скорость V равна угловой