Линейная и угловая скорость, теория и онлайн калькуляторы

Линейная и угловая скорость, теория и онлайн калькуляторы

Линейная скорость

Определение

Векторная величина равная:

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}=\frac{d\overline{r}}{dt}\left(1\right),\ }\]

называется мгновенной скоростью или просто скоростью.

В выражении (1) $\Delta \overline{r}$ — перемещение материальной точки за отрезок времени равный $\Delta t$. Скорость характеризует быстроту перемещения тела. Мгновенная скорость — это скорость в данный момент времени.

Предельный переход в выражении (1) имеет геометрический смысл. Вектор $\Delta \overline{r}$ направлен вдоль хорды, соединяющей две точки траектории, сближение этих точек ведет к тому, что этот вектор принимает положение касательной к траектории движения в данной точке. Получается, что вектор мгновенной скорости направлен по касательной к траектории движения. При прямолинейном движении вектор скорости направлен по прямой.

Скорость прохождения пути определена аналогично:

\[v={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\left(2\right).\ }\]

Если траектория движения материальной точки — плавная кривая, то чем короче дуга, тем ближе она по длине к длине хорды. В предельном переходе при$\ \Delta t\to 0$ можно считать, что $\Delta s\to \Delta r$. Следовательно,

\[v={\mathop{lim}_{\Delta t\to 0} \frac{\Delta r}{\Delta t}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{dr}{dt}=\frac{ds}{dt}\left(3\right).\ }\ }\]

Если представить радиус — вектор, определяющий положение материальной точки $\overline{r}$ в декартовой системе координат как:

\[\overline{r}=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}+z\left(t\right)\overline{k}\left(4\right),\]

где $\overline{i}$; $\overline{j}$; $\overline{k}$ — единичные орты соответствующих осей координат, постоянные во времени, то подставив правую часть выражения (4)
в определение линейной скорости (1), получим:

\[\overline{v}=\overline{i}\frac{dx}{dt}+\overline{j}\frac{dy}{dt}+\overline{k}\frac{dz}{dt}\left(5\right). 2_z}.\]

Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:

\[\left[v\right]=\frac{\left[s\right]}{\left[t\right]}.\]

В Международной системе единиц (СИ) единицей измерения линейной скорости (в том числе и средней скорости) является метр в секунду:

\[\left[v\right]=\frac{м}{с}.\]

Угловая скорость

Определение

Угловой скоростью называют векторную величину, равную первой производной от угла поворота по времени:

\[\overline{\omega }=\frac{d\overline{\varphi }}{dt}\left(7\right).\]

Вектор угловой скорости направлен по оси вращения по правилу правого винта, то есть как вектор $d\overline{\varphi }.$

Связь между линейной и угловой скоростями задана выражением:

\[v=R\omega \left(8\right). \]

В векторном виде формулу (8) записывают как:

\[\overline{v}=\overline{\omega }\times \overline{R}\left(9\right),\]

$\overline{R}$ — вектор, соединяющий ось вращения и движущуюся точку. Модуль скорости в выражении (9) найдем как:

\[v=\omega R{\sin \alpha \ \left(10\right),\ }\]

где $\alpha $ — угол между вектором угловой скорости и $\overline{R}.$

При равномерном движении по окружности угловая скорость ($\omega =const$), частота и период связаны как:

\[\omega =\frac{2\pi }{T}=2\pi \nu \left(11\right).\]

Единица измерения угловой скорости — это радиан, деленный на секунду:

\[\left[\omega \right]=\frac{рад}{с}.\]

Примеры задач на линейную и угловую скорость

Пример 1

Задание: Цилиндр вращается вокруг неподвижной оси так, что угол поворота изменяется в зависимости от
времени как: $\varphi =At^2,\ где\ A=const. 2\right)=2At\ \left(1.2\right).\]

При $t=t’$ угловая скорость цилиндра равна:

\[\omega \left(t’\right)=2At’.\]

Функция $\omega (t)$, как мы видим из уравнения (1.2) является линейной, следовательно, графиком угловой скорости в осях ($\omega ,t$) ,будет прямая, выходящая из начала координат рис.1. Угол наклона прямой характеризует коэффициент $2A$.

   

Пример 2

Задание: Материальная точка движется в плоскости XOY. Ее движение описывают уравнения:

\[
\left\{ \begin{array}{c}
x=At, \\
y=At(1+Bt) \end{array} \right.
\]

$(A,B-постоянные,\ больше\ нуля)$. Запишите закон изменения скорости движения точки ($\overline{v}(t)$). Каков модуль скорости движения точки?

Решение: Закон движения точки задан в координатной форме. В векторном виде его запишем как:

\[\overline{r}\left(t\right)=x\overline{i}+y\overline{j}=At\overline{i}+At\left(1+Bt\right)\overline{j}\left(2. 2}$

   

Читать дальше: механические колебания и волны.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Угловая скорость против линейной скорости: 3 важных понятия

Мы уже знали концепцию скорость. Теперь посмотрим на подробное сравнение угловая скорость Против линейной скорости.

Когда предметы движутся в круговом направлении, можно увидеть линейную скорость и угловую скорость. Давайте разберемся в сравнении угловая скорость Vs линейная скорость в деталях.

Угловая скорость против линейной скорости

Можно построить характеристики, связанные с движением по окружности, глядя на взаимосвязь между дугой на окружности и радианным углом, который она образует. Прежде чем углубляться в эти две концепции угловой скорости и линейной скорости, сначала нам нужно понять значение линейного смещения и углового смещения.

Кредиты на изображения: “Merry Go Round — Дворцовый пирс, Брайтонн»(CC BY 2.0) от Марк Ворди

Мы уже знаем, что угловое смещение определяется как угол, нарисованный частицей при движении по кругу. Поскольку направление смещения параллельно оси, угловое смещение в этом случае представлено осевым вектором.

Смещения, испытываемые частицей при круговом движении, делятся на две категории. Это следующие:

1. Линейное смещение по окружности
2. Угловое смещение, составляющее угол

Если радиус круга равен ‘r’, то соотношение между линейным смещением и угловым смещением может быть выражено как:

  s = rθ или θ = s / r

Теперь линейная скорость определяется как скорость изменения линейного смещения. Линейное смещение частицы можно задать следующим образом:

А когда дело доходит до частиц, их угловая скорость определяется как скорость, с которой изменяется их угловое смещение.

∴ В простом смысле линейная скорость относится к скорости, с которой длина дуги изменяется во времени, тогда как угловая скорость относится к скорости, с которой угол вокруг центральной точки изменяется с течением времени.

Связь между угловой скоростью и линейной скоростью

Только что мы видели, что линейная скорость частицы задается как

И мы знаем, что s = r 

r = радиус круга постоянный

Из уравнения угловой скорости мы знаем, что

Поэтому связь между линейной и угловой скоростями тела, движущегося в равномерное круговое движение дан кем-то : 

Как указано в этом уравнении, линейная скорость (v) частицы прямо пропорциональна ее расстоянию от центра кругового пути и угловой скорости частицы.

Сравнительный анализ угловой скорости и линейной скорости

Мы можем провести сравнение, основываясь на нашем понимании терминов угловой скорости и линейной скорости, как показано в таблице ниже:

Угловая скорость	Линейная скорость
Угловая скорость частицы определяется как скорость изменения углового смещения.	Линейная скорость определяется как скорость изменения линейного смещения.
Угловая скорость частицы измеряется по оси круга. Во время кругового движения он остается постоянным.	При круговом движении линейная скорость частицы проходит по окружности круга. Он меняется в зависимости от положения точки на окружности.
Угловая скорость обозначается символом	Линейная скорость обозначается символом
Формула определяется следующим образом:	Формула определяется следующим образом:
Он имеет форму осевого вектора. Это связано с тем, что смещение частицы направлено в направлении центральной оси круга.	Это векторная величина, что означает, что с ней связаны как величина, так и направление.
Единица измерения угловой скорости — градусы и радианы. Где градус безразмерен, а радианы — это единица СИ.	Единица измерения линейной скорости м / с.

---

Часто задаваемые вопросы

В. Что такое скорость?

Ответ: Скорость, с которой что-либо движется или действует, называется его скоростью.

Слова скорость и скорость дают нам представление о том, насколько быстро или медленно объект движется по отношению к нашему положению.

Мы сталкиваемся с ситуациями, когда нам нужно определить, какая из двух или более вещей движется быстрее, чем другая. Это случается очень часто. Скорость объекта определяется как скорость, с которой его положение изменяется по отношению к системе отсчета и во времени. Его можно измерять в метрах в секунду (мс-1).

Когда скорость тела изменяется на значительную величину или в определенном направлении, считается, что тело ускоряется.

В. Что вы подразумеваете под угловой скоростью? Приведите примеры.

Ответ: Это скорость, с которой частица вращается вокруг центральной точки.

Угловая скорость частицы определяется как скорость, с которой изменяется угловое смещение частицы. Угловая скорость частицы находится вдоль оси круга, когда предмет движется по кругу. Другими словами, угловая скорость является постоянной величиной и обозначается «ω».

Примерами угловой скорости являются колесо обозрения., Земля, Колесо автобуса и Вентилятор.

В. Что вы подразумеваете под линейной скоростью? Приведите примеры.

Ответ: По сути, это скорость, с которой частица движется по прямой траектории.

Линейная скорость может быть определена как скорость, с которой линейное смещение изменяется во времени. И угловая, и линейная скорости присутствуют во всем, что вращается или движется по кругу.

Например, рассмотрите возможность катания на карусели. Камень, брошенный с края вращающейся карусели, не упадет прямо вниз. Вместо этого он продолжит двигаться с той же скоростью, на которой двигалась карусель, когда был брошен камень. Это линейная скорость гальки.

В. Если объект преодолевает расстояние 5 метров за 2 секунды. Тогда какой будет линейная скорость этого объекта?

Ответ: Линейную скорость можно рассчитать, используя простую формулу.

Дано: смещение = 5 метров, время = 2 секунды.

Линейная скорость:  = с / т 

∴= 5 / 2 

∴= 2.5 м / с 

∴ Линейная скорость объекта равна 2.5 м / с

В. Идентичны ли угловая скорость и угловая скорость?

Ответ: Обе величины имеют сходства и различия.

Сходства между ними заключаются в их единицах измерения радиан / секунда. При этом они различаются в аспекте скалярного и векторного. Угловая скорость () является скалярной величиной, тогда как угловая скорость () — векторная величина.

В. Идентичны ли линейная скорость и линейная скорость?

Ответ: Хотя и скорость, и скорость стремятся определить расстояние до движущегося объекта, они в некоторых отношениях различаются.

Во-первых, скорость — это скалярная величина. Таким образом, выражение скорости в м / с просто показывает величину. Это ничего не говорит о движении объекта. Однако линейная скорость описывает направление, в котором что-то движется.

Это связано с тем, что скорость является векторной величиной, которая указывает как величину, так и направление движущегося тела.

---

Связь между угловой скоростью и линейной скоростью

Движение описывается как изменение положения в течение определенного периода времени. С точки зрения физики и механики это называется скоростью. Он определяется как изменение позиции за период. Вращательное движение касается тел, которые движутся вокруг фиксированной оси. Эти тела во вращательном движении часто демонстрируют поведение, аналогичное их поведению во время поступательного движения. Например, угловая скорость и скорость при поступательном движении аналогичны, а также крутящий момент-сила и масса-момент инерции.

Угловое вращение

Вращательное движение — это круговое движение вокруг фиксированной оси. Работая над задачами о вращательном движении, мы пытаемся найти сходство между поступательным и вращательным движением и использовать аналогичные переменные. Угол поворота определяется углом, охватываемым телом. Он обозначается обозначением тета(). При вращательном движении объект совершает круговое движение. Длина дуги – это расстояние, пройденное объектом во вращательном движении. Это расстояние и угловой поворот связаны радиусом кривизны.

Обозначим длину дуги буквой «s», а радиус кривизны буквой «r».

θ = s/r 

Угловая скорость

Предположим, что тело вращается вокруг некоторой фиксированной оси. Затем тело меняет свой угол со временем. Обозначая угол через θ, угловая скорость определяется как скорость изменения угла тела. Угловая скорость обозначается ω. Если тело вращается с постоянной скоростью, используется средняя угловая скорость,

В случаях, когда вращательное движение непостоянно, вычисляется мгновенная угловая скорость.

ω = dθ/dt

Как показано на рисунке, угловая скорость направлена ​​к неподвижной оси.

Угловая скорость и линейная скорость

Линейная скорость — это мера расстояния, которое объект проходит за единицу времени. Для объекта, движущегося по кругу, линейная скорость связана с угловой скоростью. Объект, покрывающий угол, также покрывает некоторое расстояние по дуге окружности. Предположим, что линейная скорость частицы P, вращающейся вокруг фиксированной оси, определяется выражением

Известно, что

s = rθ

.

|в| = rω

Примеры задач

Вопрос 1: Найдите угловую скорость мяча, движущегося со скоростью 10 м/с по окружности радиусом 20 м.

Ответ:

Связь между угловой и линейной скоростью мяча определяется выражением, 

|v| = rω

Дано:

v = 10 м/с

r = 20 м

Найти:

ω = ?

v = rω

⇒ 10 = (20)ω

⇒ 0,5 м/с = ω

Вопрос 2. Найдите угловую скорость мяча, движущегося со скоростью 100 м/с по радиусу 5 м. круг.

Ответ:

Связь между угловой и линейной скоростью мяча определяется выражением

|в| = rω

Дано:

v = 100 м/с

r = 5 м

Найти:

ω = ?

v = rω

⇒ 100 = (5)ω

⇒ 20 м/с = ω

Вопрос 3. Найти полный круг за 20 секунд. Найдите угловую скорость частицы.

Ответ:

Угловая скорость определяется как

ω = (угол)/(время)

Дано:

Угловая скорость =

003

= 2π

Время «t» = 20 секунд.

Найти:

ω = (угол)/(время)

⇒ ω = 2π / 20

⇒ ω = π /10 рад/с.

Вопрос 4: Найдите покрытия на 270 градусов за 5 секунд. Найдите угловую скорость частицы.

Ответ:

Угловая скорость определяется как

ω = (угол)/(время)

Дано:

= 9003/9003 9003/9003 9003 9003 9003 9003 003

Время «t» = 5 секунд.

Найти:

ω = (угол)/(время)

⇒ ω = 3π / (4)(5)

⇒ ω = 3π /20 рад/с.

⇒ ω = 0,15π рад/с.

Вопрос 5: Планета движется вокруг своего солнца по кругу. Угловая скорость планеты 0,5 рад/с. Расстояние планеты от Солнца оценивается в 1 00 000 км. Найдите линейную скорость планеты.

Ответ:

Связь между угловой и линейной скоростью мяча определяется выражением, 

|v| = Rω

Дано:

ω = 0,5 рад/с

R = 10 ⁵ км

⇒ R = 10 ⁸ M

Найти:

V =?

v = rω

⇒ v = (10 ⁸ )(0,5)

⇒ 5 × 10 ⁷ м/с = v

6,1 Угол поворота

Цели обученияУгол вращенияУгловая скоростьРешение задач, связанных с углом вращения и угловой скоростьюТренировочные задачиПроверка понимания

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Описывать угол поворота и связывать его с его линейным аналогом
• Опишите угловую скорость и свяжите ее с ее линейным эквивалентом
• Решение задач на угол поворота и угловую скорость

«>

Основные термины раздела

угол поворота	угловая скорость	длина дуги
круговое движение	радиус кривизны	вращательное движение
вращение	тангенциальная скорость

Угол поворота

Что именно мы подразумеваем под круговым движением или вращением ? Вращательное движение – это круговое движение объекта вокруг оси вращения. Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое движение. 0272 петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.

При решении задач, связанных с вращательным движением, мы используем переменные, аналогичные линейным переменным (расстояние, скорость, ускорение и сила), но учитывающие кривизну или вращение движения. Здесь мы определяем угол поворота, который является угловым эквивалентом расстояния; и угловая скорость, которая является угловой эквивалентностью линейной скорости.

Когда объекты вращаются вокруг какой-либо оси — например, когда диск на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по круговой траектории.

Рис. 6.2. Все точки на компакт-диске движутся по круговым траекториям. Ямки (точки) вдоль линии от центра к краю перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt.

Длина дуги , , это расстояние, пройденное по круговой траектории. Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3.

Рис. 6.3 Радиус ( r ) окружности повернут на угол ΔθΔθ. Длина дуги, ΔsΔs, представляет собой расстояние, пройденное по окружности.

Рассмотрим линию от центра компакт-диска до его края. В заданное время каждая яма (используемая для записи информации) на этой линии перемещается на один и тот же угол. Угол поворота представляет собой величину поворота и является угловым аналогом расстояния. Угол поворота ΔθΔθ — это длина дуги, деленная на радиус кривизны.

Δθ=ΔсрΔθ=Δср

Угол поворота часто измеряется в радианах. (Радианы на самом деле безразмерны, потому что радиан определяется как отношение двух расстояний, радиуса и длины дуги.) Оборот — это один полный оборот, когда каждая точка на окружности возвращается в исходное положение. Один оборот покрывает 2π2π радиан (или 360 градусов) и, следовательно, имеет угол поворота 2π2π радиан и длину дуги, равную длине окружности. Мы можем преобразовать радианы, обороты и градусы, используя соотношение

1 оборот = 2π2πрад = 360°. См. Таблицу 6.1 для преобразования градусов в радианы для некоторых распространенных углов.

6,12π рад=360°1 рад=360°2π≈57,3°2π рад=360°1 рад=360°2π≈57,3°

Градусы	Радианы
30∘30∘	π6π6
60∘60∘	π3π3
90∘90∘	π2π2
120∘120∘	2π32π3
135∘135∘	3π43π4
180∘180∘	ππ

Таблица 6. 1 Обычно используемые углы в градусах и радианах

Угловая скорость

Как быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Сначала рассмотрим угловую скорость (ω)(ω) — скорость изменения угла поворота. В форме уравнения угловая скорость равна

6.2ω=ΔθΔt,ω=ΔθΔt,

, что означает, что угловой поворот (Δθ)(Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота за заданное время, он имеет большую угловую скорость. Единицами угловой скорости являются радианы в секунду (рад/с).

Теперь давайте рассмотрим направление угловой скорости, а значит мы теперь должны называть его угловой скоростью. Направление угловой скорости вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость направлена ​​от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.

Угловая скорость (ω) представляет собой угловую версию линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге (Δs)(Δs) за короткое время (Δt)(Δt), поэтому ее тангенциальная скорость равна

6.3
v=ΔsΔt.v=ΔsΔt.

Из определения угла поворота Δθ=ΔsrΔθ=Δsr видно, что Δs=rΔθΔs=rΔθ. Подставляя это в выражение для v дает

v=rΔθΔt=rω.v=rΔθΔt=rω.

Уравнение v=rωv=rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем краю компакт-диска (с большими r ), чем для точки ближе к центру компакт-диска (с меньшими r ). Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. рисунок 6.4.

Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается по большей дуге (Δs2Δs2), поскольку она находится дальше от центра вращения.

Теперь рассмотрим другой пример: шина движущегося автомобиля (см. рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое против , потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет производить большую линейную (тангенциальную) скорость v, для автомобиля. Это связано с тем, что больший радиус означает, что более длинная дуга должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.

Рис. 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят на домкрат и колеса крутились, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад относительно оси с тангенциальной скоростью v=rωv=rω, где r это радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.

Однако бывают случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда колеса автомобиля крутятся на льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля по льду длина дуги, по которой перемещаются протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.

Советы по достижению успеха

Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны указать величину и направление. Направление угловой скорости находится вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.

Рис. 6.6 Когда муха на краю старой виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена ​​по касательной к кругу. В этом случае направление угловой скорости находится на странице.

Watch Physics

Взаимосвязь между угловой скоростью и скоростью

В этом видео рассматривается определение и единицы измерения угловой скорости, а также их связь с линейной скоростью.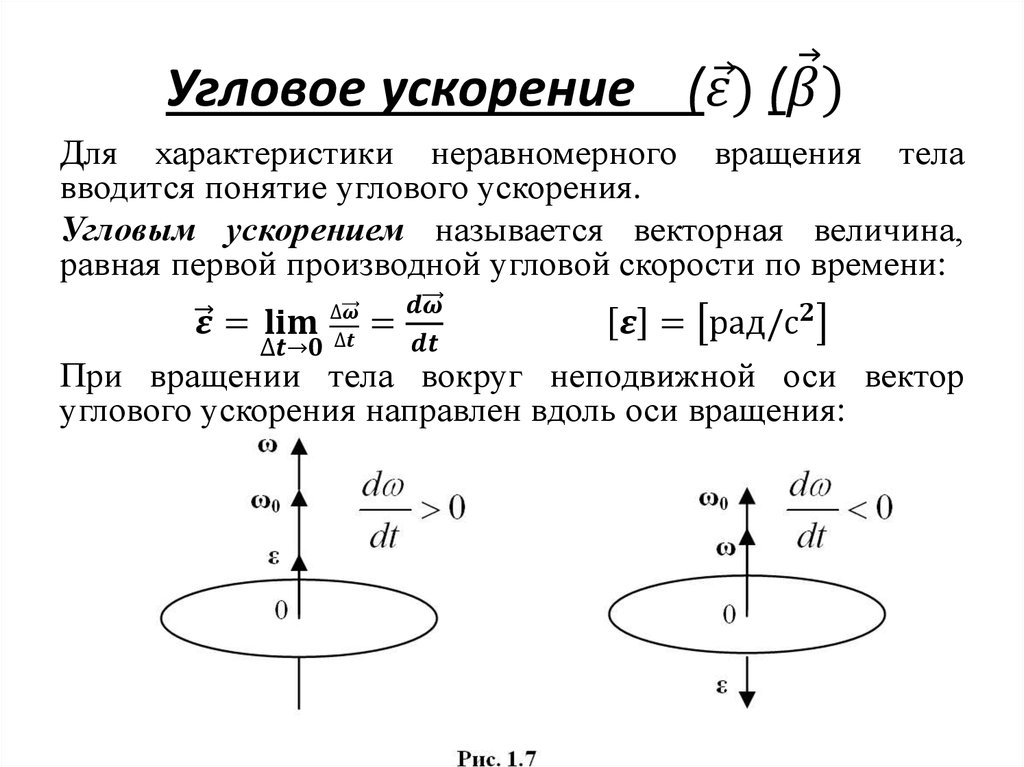 Он также показывает, как конвертировать между оборотами и радианами.

Проверка захвата

Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса траектории?

1. Да, потому что тангенциальная скорость не зависит от радиуса.
2. Да, потому что тангенциальная скорость зависит от радиуса.
3. Нет, потому что тангенциальная скорость не зависит от радиуса.
4. Нет, потому что тангенциальная скорость зависит от радиуса.

Решение задач на угол поворота и угловую скорость

Snap Lab

Измерение угловой скорости

В этом упражнении вы создадите и измерите равномерное круговое движение, а затем сопоставите его с круговыми движениями с разными радиусами.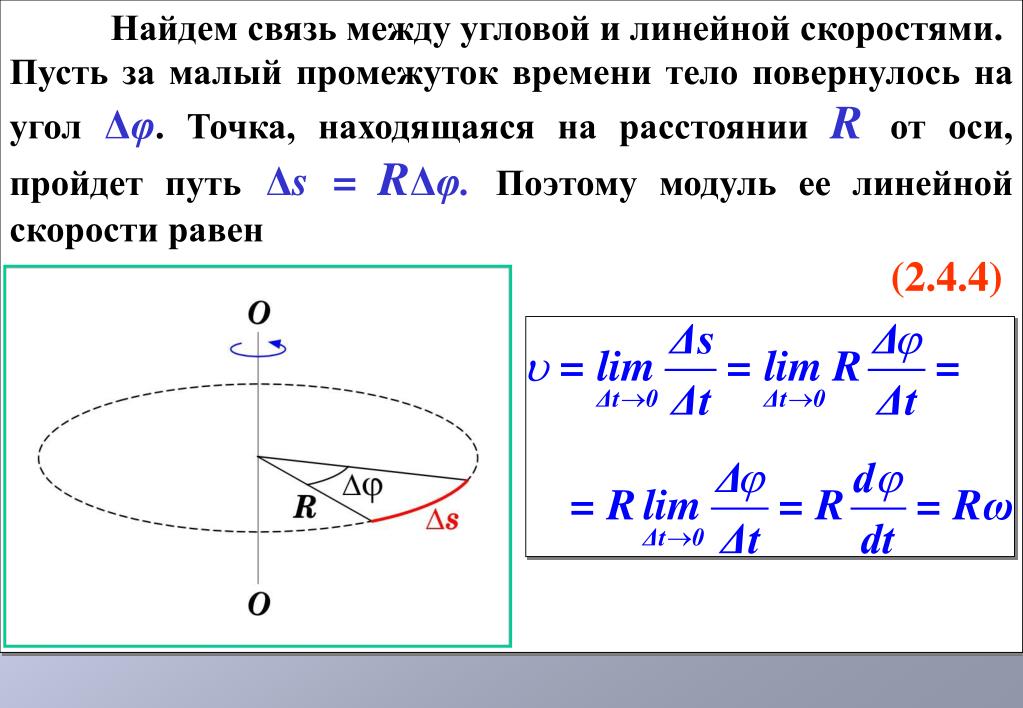

Материалы

• Одна струна (длиной 1 м)
• Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
• Один таймер

Процедура

1. Привяжите объект к концу нити.
2. Раскачайте предмет по горизонтальному кругу над головой (раскачивание запястьем). Важно, чтобы круг был горизонтальным!
3. Поддерживайте постоянную скорость объекта, пока он качается.
4. Измерьте таким образом угловую скорость объекта. Измерьте время в секундах, за которое объект совершает 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
5. Какова приблизительная линейная скорость объекта?
6. Поднимите руку вверх по веревке так, чтобы длина веревки составила 90 см. Повторите шаги 2–5.
7. Переместите руку вверх по веревке так, чтобы ее длина составила 80 см. Повторите шаги 2–5.
8. Переместите руку вверх по веревке так, чтобы ее длина составила 70 см. Повторите шаги 2–5.
9. Переместите руку вверх по веревке так, чтобы ее длина составила 60 см. Повторите шаги 2–5
10. Переместите руку вверх по веревке так, чтобы ее длина составила 50 см. Повторите шаги 2–5
11. Постройте графики зависимости угловой скорости от радиуса (т.е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.

Проверка захвата

Если вы медленно качаете объект, он может вращаться со скоростью менее одного оборота в секунду. Каковы были бы обороты в секунду для объекта, который делает один оборот за пять секунд? Какова будет его угловая скорость в радианах в секунду?

1. Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет 2π5 рад/с.
2. Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет π5 рад/с.
3. Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 10πрад/с.
4. Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 5πрад/с.

Теперь, когда у нас есть понимание концепций угла поворота и угловой скорости, мы применим их к реальным ситуациям башни с часами и вращающейся шины.

Рабочий пример

Угол поворота на башне с часами

Часы на башне с часами имеют радиус 1,0 м. а) На какой угол поворачивается часовая стрелка часов, когда она движется с 12 часов дня до 12 часов дня. до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в ​​эти два времени?

Стратегия

Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3. Получив угол поворота, мы можно определить длину дуги, переформулировав уравнение Δθ=ΔsrΔθ=Δsr, поскольку радиус задан.

Решение задачи (a)

При переходе от 12 к 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в ​​положении 12 и 3 равен 14×2π рад=π214×2π рад=π2 (т. е. 90 градусов).

Решение (б)

Преобразовывая уравнение

6.4Δθ=Δsr,Δθ=Δsr,

получаем

6.5Δs=rΔθ.Δs=rΔθ.

Подстановка известных значений дает длину дуги

6,6Δs=(1,0 м)(π2 рад)=1,6 мΔs=(1,0 м)(π2 рад)=1,6 м

Обсуждение

Мы смогли убрать радианы из окончательного решения в часть (b), поскольку радианы на самом деле безразмерны. Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.

Рабочий пример

Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). Смотрите этот рисунок.

Стратегия

В этом случае скорость протектора шины относительно оси шины равна скорости автомобиля относительно дороги, поэтому мы имеем v = 15,0 м/с. Радиус шины равен r = 0,300 м. Поскольку мы знаем v и r , мы можем изменить уравнение v=rωv=rω, чтобы получить ω=vrω=vr и найти угловую скорость.

Решение

Для нахождения угловой скорости используем соотношение: ω=vrω=vr.

Вставка известных количеств дает

6,7ω=15,0 м/с0,300 м=50,0 рад/с.ω=15,0 м/с0,300 м=50,0 рад/с.

Обсуждение

Когда мы отбрасываем единицы измерения в приведенном выше расчете, мы получаем 50,0/с (т. е. 50,0 в секунду, что обычно записывается как 50,0 с ⁻¹ ). Но угловая скорость должна иметь единицы рад/с. Поскольку радианы безразмерны, мы можем подставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. У них будет угловая скорость

6,8ω=15,0 м/с1,20 м=12,5 рад/сω=15,0 м/с1,20 м=12,5 рад/с

Практические задачи

Чему равен угол в градусах между часовой и минутной стрелками часов, показывающих 9 часов утра?

1. 0°
2. 90°
3. 180°
4. 360°

Каково приблизительное значение длины дуги между часовой и минутной стрелками часов, показывающих 10:00, если радиус часов равен 0,2 м?

1. 0,1 м
2. 0,2 м
3. 0,3 м
4. 0,6 м

Проверьте свое понимание

Упражнение 1

Что такое круговое движение?

1. Круговое движение — это движение объекта по линейной траектории.
2. Круговое движение — это движение объекта по зигзагообразной траектории.
3. Круговое движение — это движение объекта по круговой траектории.
4. Круговое движение — это движение объекта по окружности окружности или вращение по круговой траектории.

Упражнение 2

Что подразумевается под радиусом кривизны при описании вращательного движения?

1. Радиус кривизны — это радиус кругового пути.
2. Радиус кривизны — это диаметр кругового пути.
3. Радиус кривизны – это длина окружности окружности.
4. Радиус кривизны — это площадь кругового пути.

Упражнение 3

Что такое угловая скорость?

1. Угловая скорость – это скорость изменения диаметра кругового пути.
2. Угловая скорость – это скорость изменения угла, образуемого круговой траекторией.
3. Угловая скорость — это скорость изменения площади кругового пути.
4. Угловая скорость – это скорость изменения радиуса кругового пути.

Упражнение 4

Какое уравнение определяет угловую скорость ω? Предположим, что r — радиус кривизны, θ — угол, t — время.

1. ω=ΔθΔt
2. ω=ΔtΔθ
3. ω=ΔrΔt
4. ω=ΔtΔr

Упражнение 5

Найдите три примера объекта, движущегося по кругу.

1. искусственный спутник Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
2. искусственный спутник на орбите Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра
3. Земля, вращающаяся вокруг своей оси, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра.