Содержание
Угловая скорость против углового ускорения: 3 важных факта
Концепции угловая скорость и угловое ускорение — наиболее известные концепции, объясняющие, как быстро тело может изменять свое положение и как быстро оно движется по круговой траектории.
Когда вы вращаете шар по круговой орбите, он вращается под определенным углом с определенной скоростью — эта скорость приводит к ускорению. Давайте обсудим угловую скорость и угловое ускорение в этом посте.
Угловая скорость:
Мы обсуждали угловую скорость в предыдущей статье.
Дифференциальное изменение смещения объекта, вращающегося по круговой орбите на угол θ, во времени называется угловой скоростью.
Изображение кредита: «Машины на кольцевой развязке крутятся…» by тинзиюн под лицензией CC BY 2.0
Формула для угловой скорости:
Угловое ускорение:
Концепция угловое ускорение похоже на линейное ускорение.
Скорость изменения скорости объекта, вращающегося под углом θ по круговой орбите, во времени называется угловым ускорением.
Обозначается греческой буквой ‘α.
Угловое ускорение
Если тело движется по круговой траектории со скоростью ωi первоначально и меняет свою скорость на ωf, то ускорение движущегося тела определяется выражением
Но ∆ω = ωf -ω0
Угловое ускорение определяется разностью угловых скоростей начальной и конечной скорости.
Угловая скорость против углового ускорения
Сравнение угловой скорости и углового ускорения приведено в таблице ниже, которая может помочь вам понять.
| Угловая скорость | Угловое ускорение |
| Дифференциация углового смещения во времени дает угловую скорость. | Дифференцирование времени углового смещения второго порядка дает угловое ускорение. |
| Единица угловой скорости — радианы в секунду. | Единица углового ускорения — радиан в секунду.2 . |
| Размерная формула угловой скорости [M0L0T-1] | Размерная формула углового смещения [M0L0T-2] |
У него есть величина, но направление меняется вместе с осями координат; следовательно, это псевдовекторная величина.
|
У него есть величина и определенное направление, которое остается неизменным на протяжении всего действия; следовательно, это векторная величина. |
| Радиус круговой орбиты не влияет на угловую скорость. | Радиус круговой орбиты оказывает обратное влияние на угловое ускорение. |
Факты, связанные с угловой скоростью и угловым ускорением:
- В двумерном пространстве угловое ускорение может менять знак или инвертироваться координатами. Это называется псевдоскалярной величиной.
- Когда скорость вращающегося объекта увеличивается, ускорение положительное.
Когда вы включаете вентилятор, он начинает вращаться с нуля и продолжает увеличиваться каждый раз, когда вы поворачиваете наконечник, чтобы получить больше воздуха. В этом случае ускорение положительное.
- Когда скорость уменьшается при вращении, угловое ускорение становится отрицательным.
Всякий раз, когда если повернуть головку вентилятора против часовой стрелки, чтобы снизить скорость, можно наблюдать отрицательное ускорение.
- В случае увеличения угловой скорости угловое ускорение и скорость будут в одном направлении.
- Угловое ускорение будет действовать противоположно угловой скорости всякий раз, когда скорость уменьшается.
- На равномерной круговой орбите вектор скорости имеет постоянную величину.
- Угловое ускорение станет нулевым на равномерной круговой орбите.
- Угловое ускорение уменьшается на траектории вращения максимального радиуса.
Решенные проблемы.
Автомобиль движется по круговой траектории. Первоначально угловая скорость автомобиля составляет 26 км / час, а через 34 минуты она увеличивает свою скорость до 49 км / час. Рассчитайте угловое ускорение автомобиля.
Решение:
Начальная скорость ωi = 26 км / ч
Изменение скорости ωf = 49 км / ч
Время 34 мин = 0.56 часа
Угловое ускорение равно
α = 2.15 рад / сек2.
Tколесо цикла вращается с угловым ускорением 12рад / сек.2 через 3 секунды. Рассчитайте угловую скорость.
Решение:
Компания Угловое ускорение колеса составляет 12 рад/сек2
Время на ускорение — 3 секунды.
Угловое ускорение определяется выражением
Тогда скорость можно записать через угловое ускорение как
∆ω = α.∆t
∆ω = 12 × 3
∆ω = 36 рад / сек.
Диск радиусом 12 см вращается по круговой траектории под углом 35 °. Время, необходимое для полного вращения, составляет 12 секунд. Вычислите угловую скорость и, следовательно, узнайте угловое ускорение, если оно увеличивает свою скорость до 4 рад / сек за те же 12 секунд..
Решение:
Угол поворота = ∆θ = 35 °
Время, затрачиваемое на один полный оборот ∆t = 12 секунд
Угловая скорость определяется формулой
ω = 2. 91 рад / сек.
91 рад / сек.
Угловое ускорение определяется выражением
Скорость изменяется до 4 рад / сек на тот же интервал времени, так что угловое ускорение определяется выражением;
α = 0.090 рад / сек2.
Шина вращается с ускорением 65 рад / сек. IИзменение скорости ts равно 92 рад / сек.2. Cрассчитать время, необходимое шине для достижения заданного ускорения?
Решение:
Угловое ускорение = 65рад / сек.2
Угловая скорость = 92 рад / сек.
Угловое ускорение равно
Преобразуя приведенное выше уравнение, мы можем рассчитать время как,
∆t = 1.41 сек.
FAQ
Зависит ли угловая скорость от массы вращающегося объекта?
Да, угловая скорость обратно пропорциональна массе.
Когда предполагается, что свободно вращающееся тело определенной массы проявляет некоторую скорость, если масса больше, то скорость уменьшается.
ланьs радиус влияет на угловое ускорение?
Предположим, угловое ускорение максимальное, имеет значение радиус пути вращения.
Чем больше радиус орбиты, тем меньше притяжение объекта к центру. Это приводит к уменьшению скорости и, следовательно, к ускорению.
Почему на равномерной круговой орбите угловое ускорение равно нулю?
Угловое ускорение относится к изменению угловой скорости; необходимо изменить либо величину, либо скорость.
На равномерной круговой орбите скорость остается постоянной на всем протяжении. Ни величина, ни радиус не меняются.. Это показывает, что никакого ускорения не будет.
Одинаковы ли тангенциальное ускорение и угловое ускорение?
Есть два типа ускорения;
- Линейное ускорение
- Угловое ускорение
Когда тело ускоряется по круговой орбите, это называется угловым ускорением. Это угловое ускорение далее делится как
Это угловое ускорение далее делится как
- тангенциальный ускорение
- Радиальное ускорение
Таким образом, тангенциальное ускорение происходит от углового ускорения. Это не то же самое, что угловое ускорение.
Может ли угловое ускорение быть отрицательным?
Отрицательное угловое ускорение зависит от координатной оси, по которой действует угловая скорость.
Когда предполагается, что объект движется по круговой траектории с определенной скоростью, изменение скорости вызывает угловое ускорение. Если изменение скорости уменьшает величину, то угловое ускорение будет отрицательным.
Угловая скорость и угловое ускорение
| на главную |
к оглавлению |
Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.
Московский регион. Официально.
Пройденный путь S ,
перемещение dr, скорость v , тангенциальное и нормальное ускорение
at, и an,
представляют собой линейные величины. Для описания криволинейного движения
наряду с ними можно пользоваться угловыми величинами.
Рассмотрим более
подробно важный и часто встречаемый случай движения по окружности. В этом случае
наряду с длиной дуги окружности движение можно характеризовать утлом поворота
φ вокруг оси вращения. Величину
(1.15)
называют
угловой скоростью. Угловая скорость представляет собой вектор, направление
которого связывают с направлением оси вращения тела (рис.).
Обратим внимание на то,
что, в то время как сам угол поворота φ является скаляром, бесконечно
малый поворот dφ — векторная величина, направление которой определяется
по правилу правой руки, или буравчика, и связано с осью вращения.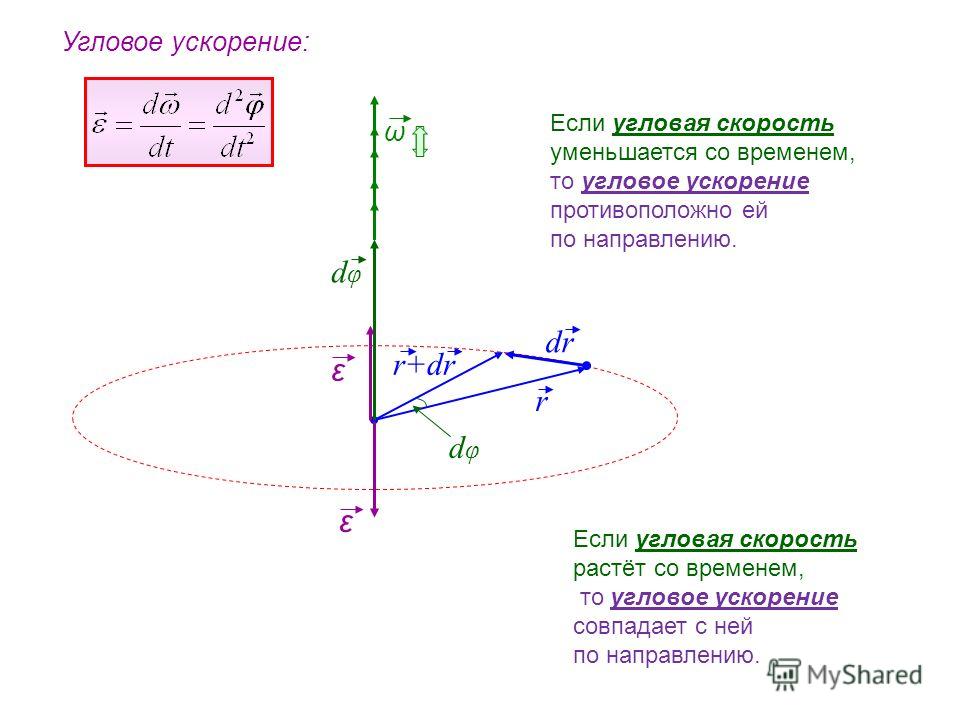 Если вращение
Если вращение
является равномерным, то ω=const и точка на окружности
поворачивается на равные углы вокруг оси вращения за равные времена. Время, за
которое она совершает полный оборот, т.е. поворачивается на угол 2π,
называется периодом движения Т. Выражение (1.15) можно
проинтегрировать в пределах от нуля до Т и получить угловую частоту
.
(1.16)
Число оборотов в единицу
времени есть величина, обратная периоду, — циклическая частота вращения
ν
=1/T. (1.17)
Нетрудно получить связь
между угловой и линейной скоростью точки. При движении по окружности элемент
дуги связан с бесконечно малым поворотом соотношением dS = R·dφ.
Подставив его в (1.15), находим
v =
ωr. (1.18)
Формула (1.18) связывает
величины угловой и линейной скоростей. Соотношение, связывающее векторы ω
Соотношение, связывающее векторы ω
и v, следует из рис. А именно, вектор линейной
скорости представляет собой векторное произведение вектора угловой скорости и
радиуса-вектора точки r:
.
(1.19)
Таким образом, вектор
угловой скорости направлен по оси вращения точки и определяется по правилу
правой руки или буравчика.
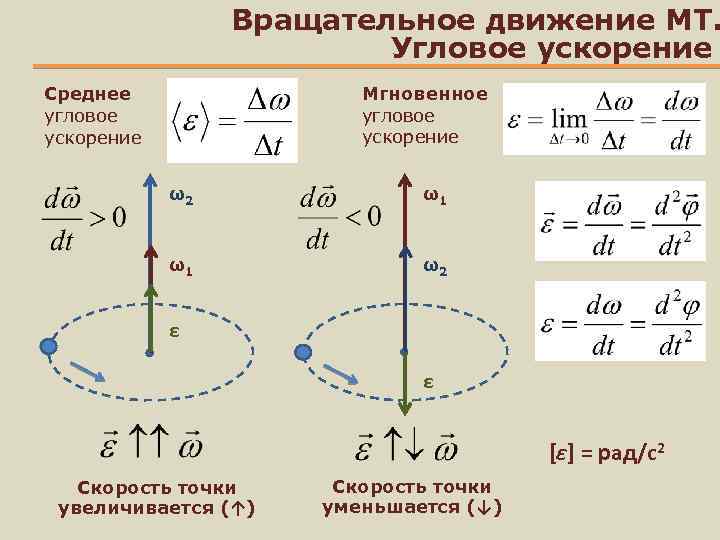
Угловое ускорение
— производная по времени от вектора угловой скорости ω (соответственно вторая
производная по времени от угла поворота)
Выразим тангенциальное и
нормальное ускорение через угловые скорости и ускорение. Используя связь
(1.18),(1.12) и (1.13), получаем
at = β·R, a =ω2·R.
(1.20)
Таким образом, для
полного ускорения имеем
.
(1.21)
Величина β играет
роль тангенциального ускорения: если β = 0. полное ускорение при вращении
полное ускорение при вращении
точки не равно нулю, a =R·ω2 ≠ 0.
5.3 Угловое ускорение – биомеханика движений человека
Угловое ускорение обозначается греческой буквой альфа (α). Угловое ускорение представляет собой скорость изменения угловой скорости во времени. Другой способ подумать об этом — как быстро что-то ускоряется или замедляется.
ускорение (α) = Δω/Δt
Единицы измерения: рад/с 2 или градус/с 2 . Когда скорость увеличивается, ускорение происходит в том же направлении вращения, чтобы увеличить скорость. Когда скорость уменьшается, должно быть ускорение в направлении, противоположном движению, действующее как тормоз, чтобы уменьшить скорость.
Ускорение имеет направление. Если объект движется в направлении против часовой стрелки (+) и набирает скорость, ускорение положительное. Если скорость уменьшается, ускорение отрицательно. Если объект движется по часовой стрелке (-) и набирает скорость, ускорение отрицательно.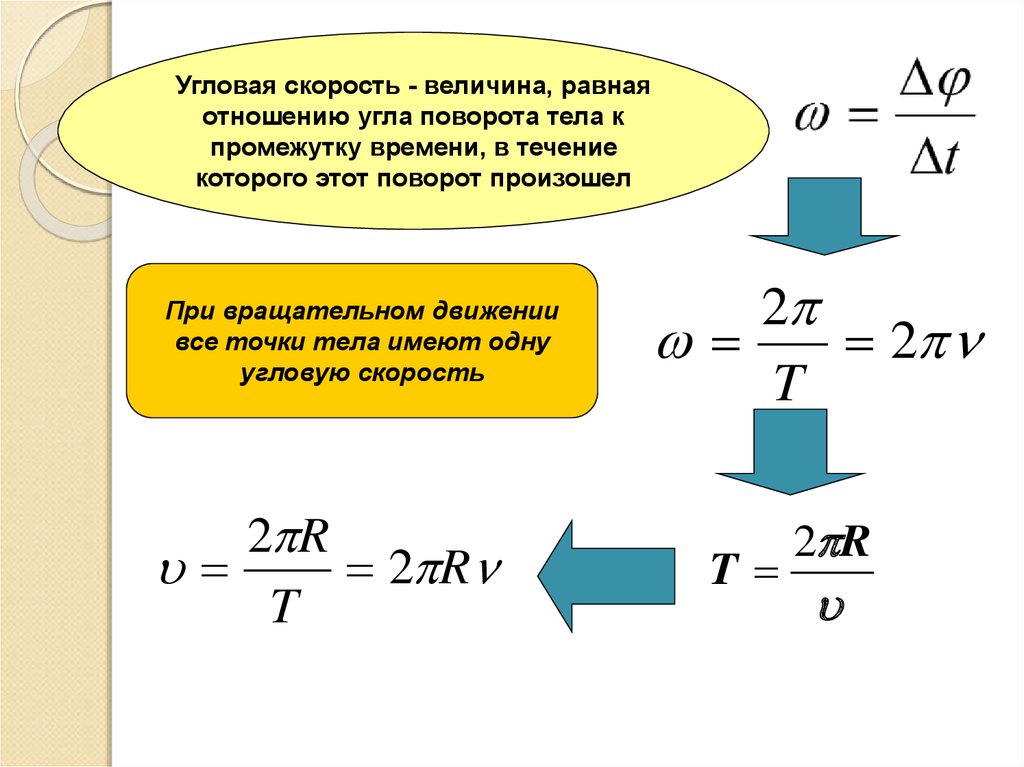 Если скорость уменьшается, ускорение положительно.
Если скорость уменьшается, ускорение положительно.
Пример 1: Расчет углового ускорения и замедления велосипедного колеса
Предположим, подросток кладет велосипед на спину и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об/мин за 5,00 с. а) Рассчитайте угловое ускорение за рад/с 2 . (b) Если теперь она ударит по тормозам, вызывая угловое ускорение -87,3 рад/с 2 , сколько времени понадобится колесу, чтобы остановиться?
Стратегия для (a)
Угловое ускорение можно найти непосредственно из его определения в [latex]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}[/latex ] потому что заданы конечная угловая скорость и время. Мы видим, что Δω составляет 250 об/мин, а Δ t — 5,00 с.
Решение задачи (a)
Введя известную информацию в определение углового ускорения, получим
[латекс]\begin{array}{lcl} \boldsymbol{\alpha} & \boldsymbol{=} & \ boldsymbol{\frac{\Delta\omega}{\Delta{t}}} \\ {} & \boldsymbol{=} & \boldsymbol{\frac{250\textbf{об/мин}}{5,00\textbf{с.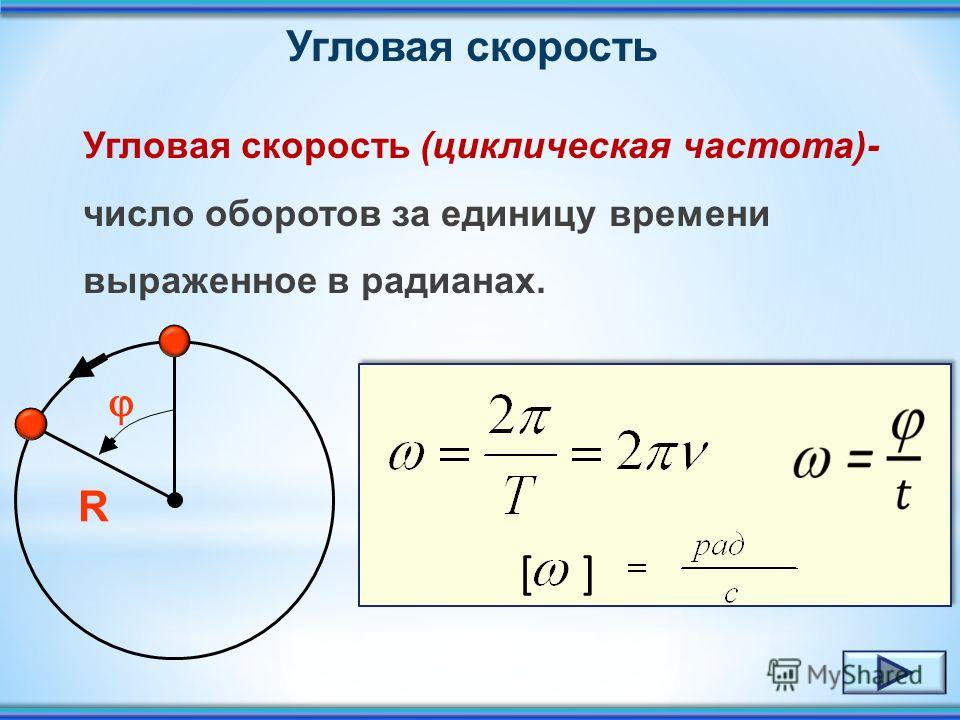 } }} \end{array}[/latex]
} }} \end{array}[/latex]
Поскольку Δω выражено в оборотах в минуту (об/мин), а нам нужны стандартные единицы измерения рад/с 2 для углового ускорения нам нужно преобразовать Δω из оборотов в минуту в рад/с:
[латекс]\begin{array}{lcl} \boldsymbol{\Delta\omega} & \boldsymbol {=} & \boldsymbol{250\frac{\textbf{оборот}}{\textbf{мин}}\cdotp\frac{2\pi\textbf{рад}}{\textbf{оборот}}\cdotp\frac{ 1\textbf{ мин}}{60\textbf{ сек}}} \\ {} & \boldsymbol{=} & \boldsymbol{26,2\textbf{ рад.}} \end{массив}[/latex]
Ввод это количество в выражение для [латекс]\жирныйсимвол{\альфа}[/латекс], мы получаем 92} \end{array}[/latex]
Стратегия для (b)
В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решив для Δ t , получив
[латекс]\boldsymbol{\Delta{t}\:=}\boldsymbol{\frac{\Delta\ omega}{\alpha}}.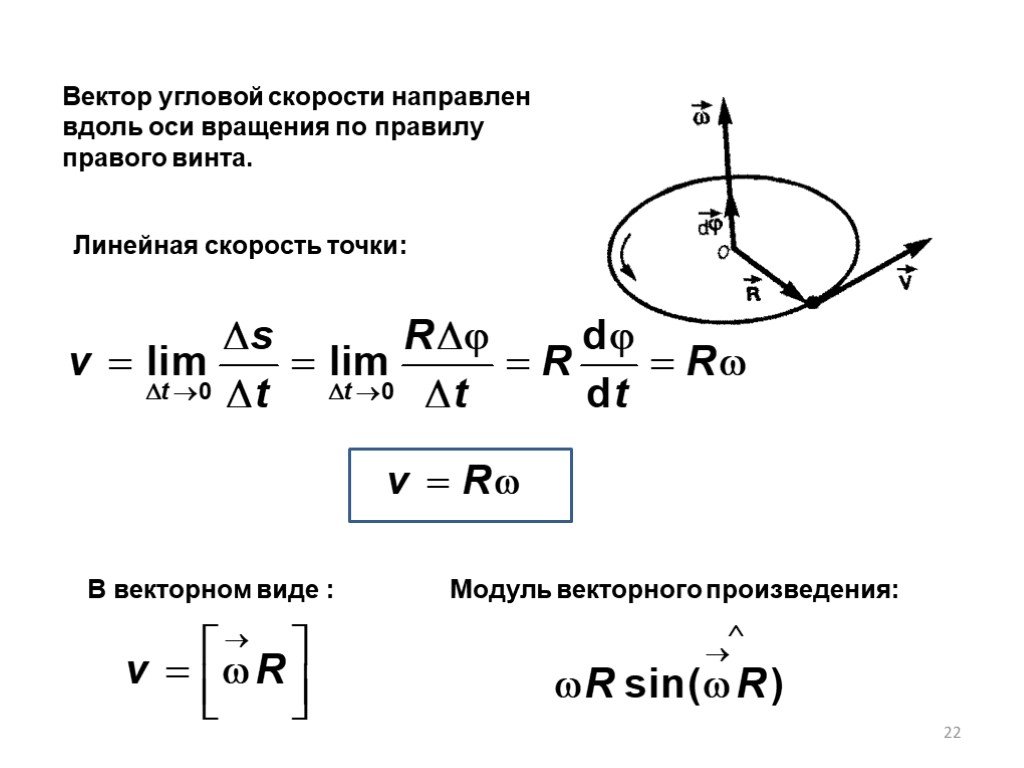 [/latex]
[/latex]
Решение для (b)
Здесь угловая скорость уменьшается с 26,2 рад/с 92}} \\ {} & \boldsymbol{=} & \boldsymbol{0.300\textbf{ с.}} \end{array}[/latex]
Обсуждение
Обратите внимание, что угловое ускорение при вращении девушки колесо маленькое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.
Если бы велосипед в предыдущем примере находился на своих колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение равно касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением а т .
При круговом движении линейное ускорение равно касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением а т .
Рисунок 2. При движении по окружности линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называется тангенциальным ускорением a t .
Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Мы знаем , что при круговом движении центростремительное ускорение a c относится к изменениям направления скорости, но не к ее величине. Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3. Таким образом, a t и a c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t напрямую связано с угловым ускорением [латекс]\жирныйсимвол{\альфа}[/латекс] и связано с увеличением или уменьшением скорости, но не с ее направлением.
Таким образом, a t и a c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t напрямую связано с угловым ускорением [латекс]\жирныйсимвол{\альфа}[/латекс] и связано с увеличением или уменьшением скорости, но не с ее направлением.
Рис. 3. Центростремительное ускорение a c возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Теперь мы можем найти точное соотношение между линейным ускорением a t и угловым ускорением [латекс]\boldsymbol{\alpha}[/латекс]. Поскольку линейное ускорение пропорционально изменению величины скорости, оно определено как
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta{v}}{\Delta{t}}. }[/latex]
}[/latex]
Для кругового движения обратите внимание, что v = r ω , так что
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}.}[/latex]
Радиус r является постоянным для кругового движения, поэтому Δ( r ω)= r (Δω) . Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r}\boldsymbol{\frac{\Delta\omega}{\Delta{t}}.}[/latex]
По определению [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}.[/latex] Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha},[/латекс]
или
[латекс] \boldsymbol{\alpha\:=}\boldsymbol{\frac{a_{\textbf{t}}}{r}.}[/latex]
Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес велосипеда, тем больше ускорение велосипеда. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении [латекс]\boldsymbol{\alpha}[/латекс].
Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении [латекс]\boldsymbol{\alpha}[/латекс].
До сих пор мы определили три величины вращения — θ , ω и [латекс]\жирныйсимвол{\альфа}[/латекс]. Эти величины аналогичны поступательным величинам x , v и a . В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Ротационный | Перевод | Отношения |
|---|---|---|
| [латекс]\boldsymbol{\theta}[/латекс] | [латекс]\boldsymbol{x}[/латекс] | [латекс] \boldsymbol{\theta=\frac{x}{r}}[/латекс] |
| [латекс]\boldsymbol{\omega}[/латекс] | [латекс]\boldsymbol{v}[/латекс] | [латекс]\boldsymbol{\omega=\frac{v}{r}}[/латекс] |
| [латекс]\boldsymbol{\alpha}[/латекс] | [латекс]\boldsymbol{a}[/латекс] | [латекс] \boldsymbol{\alpha=\frac{a_{\textbf{t}}}{r}}[/latex] |
Таблица 1. Вращательные и поступательные величины. Вращательные и поступательные величины. |
||
- Равномерное круговое движение — это движение с постоянной угловой скоростью [латекс]\жирныйсимвол{\омега=\фракция{\Delta\theta}{\Delta{t}}}.[/latex]
- При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t} }}.[/латекс]
- Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]\жирныйсимвол{а_{\текстбф{т}}=\фракция{\Delta{v}}{\Delta{t} }}.[/латекс]
- Для кругового движения обратите внимание, что v = r ω , так что
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}}.[/latex]
- Радиус r постоянен для кругового движения, поэтому Δ( r ω)= р Δω .
 Таким образом,
Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r}\boldsymbol{\frac{\Delta\omega}{\Delta{t}}}.[/latex]
- По определению, Δω/Δ t = [латекс]\boldsymbol{\alpha}[/латекс]. Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha}[/латекс]
или
[латекс]\boldsymbol{\alpha=}\boldsymbol{\frac{a _{\textbf{t}}}{r}}.[/latex]
- угловое ускорение
- скорость изменения угловой скорости во времени 903:30
- изменение угловой скорости
- разность между конечным и начальным значениями угловой скорости
- тангенциальное ускорение
- ускорение в направлении касательной к окружности в интересующей точке при круговом движении
Основы углового ускорения и момента инерции
Угловое ускорение и момент инерции в конструкции машин
Как поставщика гибких приводных муфт и предохранительных муфт с шариковой фиксацией, нас часто просят оказать небольшую помощь в расчете крутящего момента, особенно для клиентов, желающих модернизировать существующее оборудование. 2). Приведенное ниже уравнение определяет скорость изменения угловой скорости.
2). Приведенное ниже уравнение определяет скорость изменения угловой скорости.
ω = угловая скорость в стандартных единицах СИ в радианах в секунду (рад/сек), 1 радиан = 57,3 градуса
t = время ускорения в секундах минута об/мин
В следующем примере угловая скорость будет рассчитана для ускорения от 0 до 60 об/мин за одну секунду. Обратите внимание, что 2π радиан в секунду = 60 об/мин.
Этот расчет очень полезен при проектировании машин, поскольку произведение углового ускорения на момент инерции вращения равно крутящему моменту. Имейте в виду, что точный момент инерции может быть трудно рассчитать на основе сложной геометрии в реальных приводных линиях, а другие переменные, такие как трение, не учитываются в следующем расчете. Тем не менее, он по-прежнему очень полезен для аппроксимации требований к крутящему моменту или установления базовых минимальных значений для определения размеров компонентов.
Дж = момент инерции в кг∙м 2
T= крутящий момент в Н∙м
Н= сила в ньютонах
кг= масса в килограммах
м 90 радиус рычага0
В последнем примере ниже мы будем использовать угловое ускорение, найденное выше, для расчета крутящего момента на маховике радиусом 1 метр и массой 1000 кг.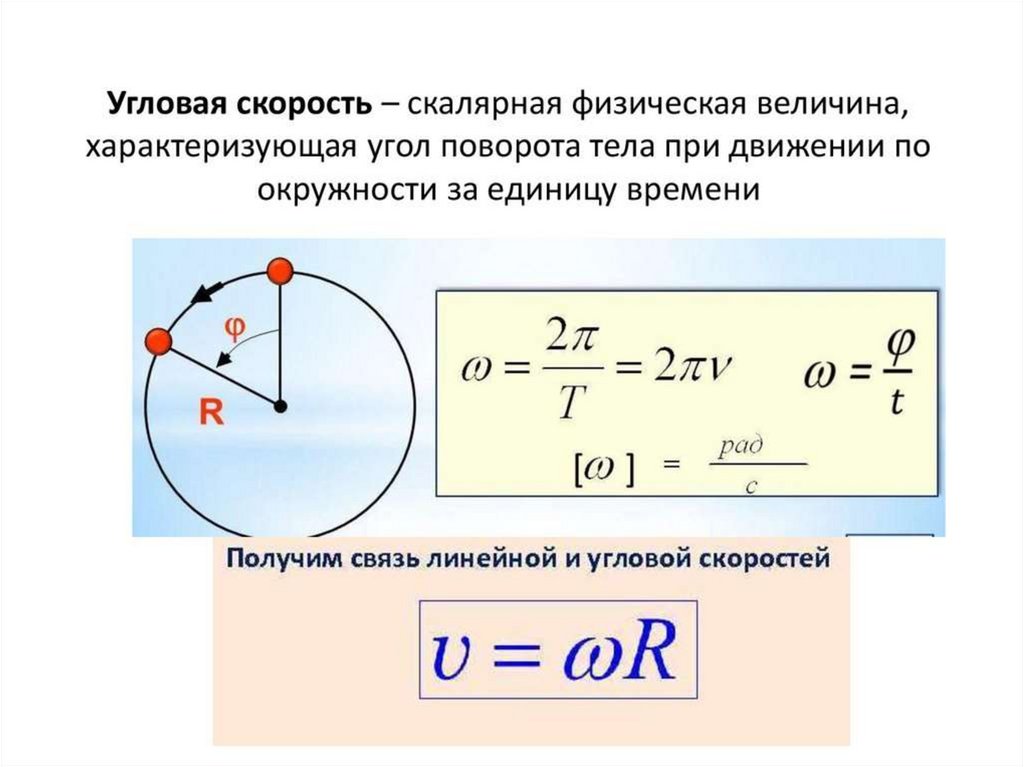
 Таким образом,
Таким образом,