Что называется угловой скоростью и угловым ускорением тела? Напишите формулы для их определения.

Угловой скоростью тела называется
физическая величина, характеризующая
быстроту изменения угла поворота

тела во времени, то есть:
.
Угловая скорость равна первой производной
по времени от угла поворота тела.

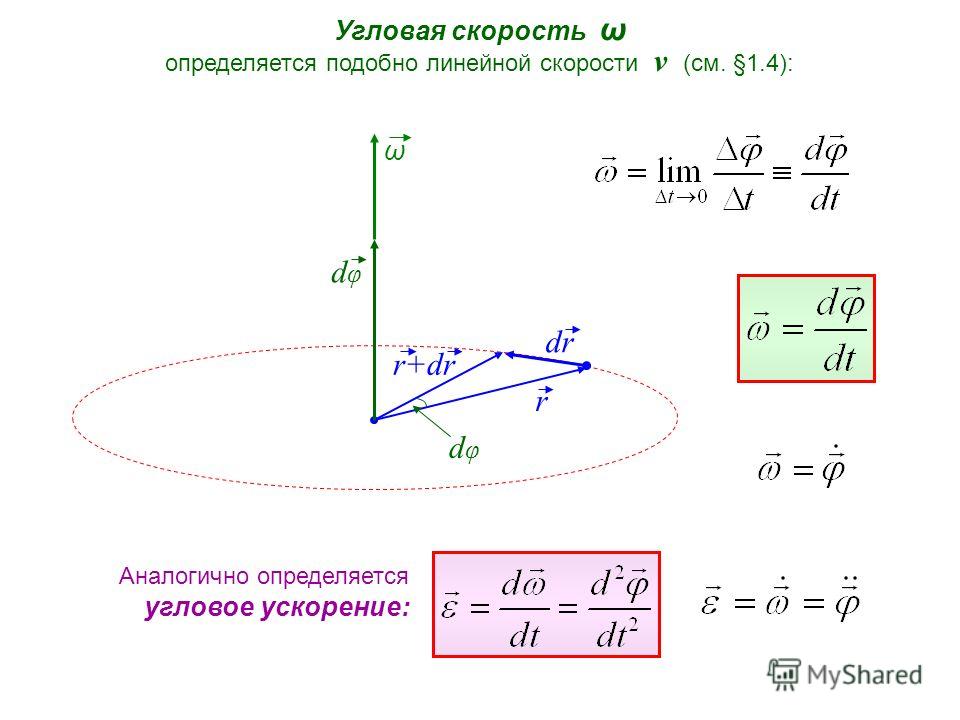
Угловым ускорением называется такая
физическая величина, характеризующая
быстроту изменения угловой скорости
тела во времени:
.
Угловое ускорение тела в данный момент
времени равно первой производной по
времени от угловой скорости или второй
производной от угла поворота.

15. Какое вращение твердого тела называется равномерным, какое равномерно-переменным? Запишите уравнения равномерного и равнопеременного вращательного движения.

— Вращение тела называют равномерным,
если угловая скорость тела постоянна,
то есть угловое ускорение равно нулю:
,
.

— Равнопеременным вращением называется
такое вращательное движение тела, при
котором его угловое ускорение постоянно
(угловая скорость с каждым одинаковым
промежутком времени изменяется да одну
и ту же величину):
,
.

Равномерное:

=>

=>
.
Произвольную константу С определяем
из начального условия:
.
В результате находим:
.
Тогда:

— з-н равномерного вращательного движение
твёрдого тела.

Равнопеременное:

=>

=>
.
Произвольную константу С определяем
из начального условия:
.
Тогда:

— з-н изменения угловой скорости при
равнопеременном вращательном движении
твёрдого тела.

Далее:

=>

=>
.
Произвольную константу С определяем
из начального условия:
.
В результате находим:
.
Окончательно:

— з-н равнопеременного вращательного
движения твёрдого тела.

16. Какая зависимость существует между
    угловой скоростью вращающегося тела
    и числом его оборотов в минуту?

,
n – число оборотов в минуту
[об/мин],

— угловая скорость [].

Пример: n=23 об/мин, найти
угловую скорость

тела. Решение:
.

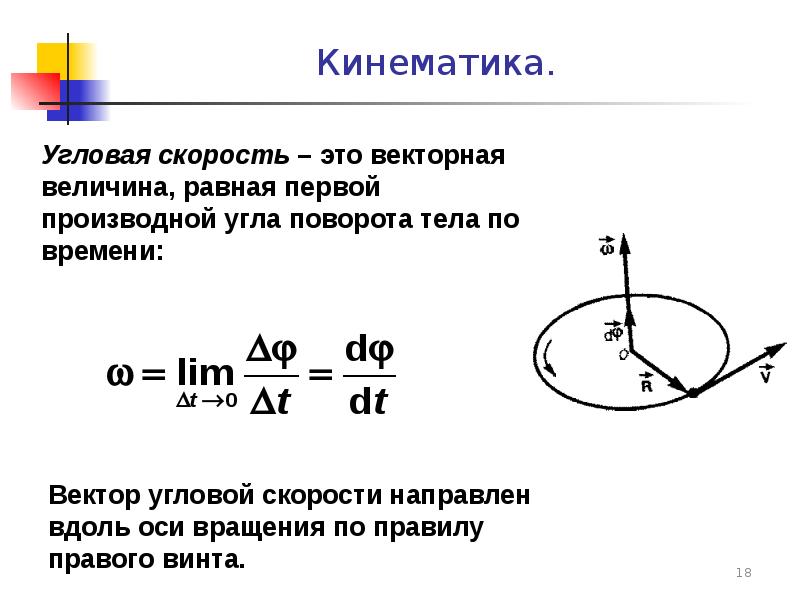
17. Как изображается угловая скорость
    тела в виде вектора, как определить
    направление этого вектора?

Вектор
угловой скорости тела направлен вдоль
оси вращения так, чтобы наблюдатель,
смотрящий с его конца видел вращение
тела против хода часовой стрелки.

18. Как выражается зависимость между
    угловой скоростью вращающегося тела
    и линейной скоростью какой-нибудь точки
    этого тела?

Линейная скорость какой-либо точки
вращающегося твёрдого тела равна
произведению угловой скорости тела на
расстояние от этой точки до оси вращения.

,
то есть:
.
Модуль
,
вектора

равен:
.

19. Напишите формулы для определения
    касательного и нормального ускорения
    точки твёрдого тела, вращающегося
    вокруг неподвижной оси.
    

Определим тангенциальное и нормальное
ускорения точки во вращательном движении
вокруг неподвижной оси:
,
.
Модуль полного ускорения точки равен:
.

20. Напишите векторные формулы для
    скоростей и ускорений точек тела,
    вращающегося вокруг неподвижной оси.

Твёрдое тело вращается вокруг неподвижной
оси Оz с угловой скоростью
.

— Определим скорость произвольной точки
М этого тела:

Угловая

— вектор угловой скорости.

Линейная

Вектор скорости любой точки тела,
вращающегося вокруг неподвижной оси,
равен векторному произведению вектора
угловой скорости тела на радиус-вектор
этой точки, проведённый из произвольного
центра, взятого на оси вращения.

— Определим ускорения произвольной
точки М этого тела:

Угловое

— вектор углового ускорения.

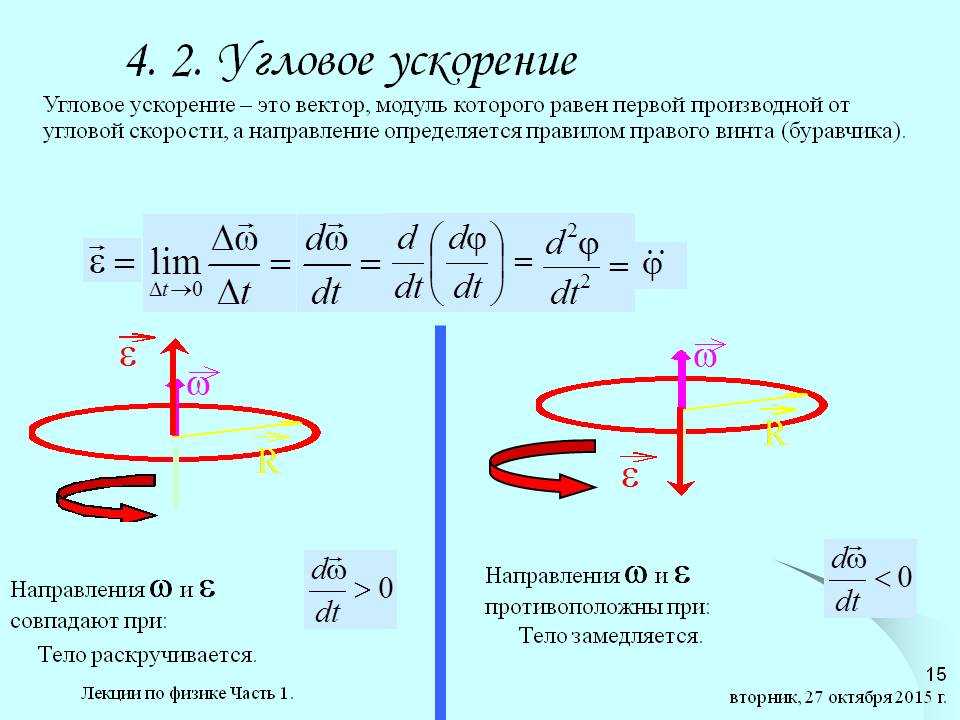
Вектор углового ускорения
,
так же как и вектор угловой скорости
,
лежит на си вращения. При этом в случае
ускоренного вращения вектор

направлен в ту же сторону, что и вектор
,
в случае же замедленного вращения вектор

направлен в сторону, противоположную
вектору
.

Полоное

или

Найдём модули ускорений:

Угловая скорость — frwiki.wiki

«Скорость вращения» перенаправляется сюда. Для других значений см Скорость (значения) и Вращение .

«Угловая частота» перенаправляется сюда. Для других значений, см. Частота (значения) .

Угловая скорость (или скорость вращения ) представляет собой величину, которая представляет собой отношение от угла поворота в момент .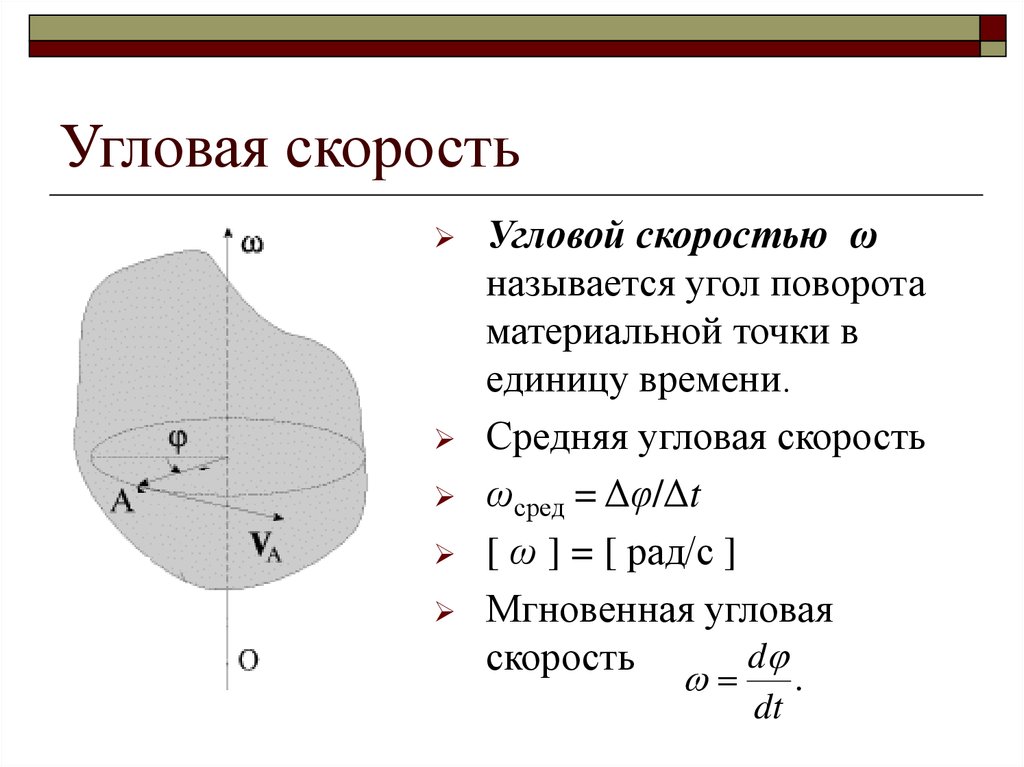 Это является аналогом, для вращательного движения, от скорости для поступательного движения .

• Когда время ограничено, мы говорим о средней угловой скорости .
• Когда время бесконечно мало, мы говорим о мгновенной угловой скорости или просто об угловой скорости . Затем угловая скорость определяется как производная по времени от углового положения вращающегося объекта. Производная по времени от угловой скорости — это угловое ускорение .

Резюме

• 1 шт.
  • 1.1 Эквивалентность единиц
• 2 измерение
• 3 Вектор угловой скорости
• 4 Примечания и ссылки
• 5 См. Также
  • 5.1 Библиография
  • 5.2 Статьи по теме

Единицы измерения

Единица угловой скорости в Международной системе является радиан в секунду (рад / с или рад с ^-1 ). Его не следует выражать в герцах (Гц), до которых нельзя привести радиан в секунду.

В области промышленной механики и повседневной жизни это часто выражается в оборотах в минуту (об / мин).

Вы также можете использовать градусы в секунду и обороты в секунду.

Эквивалентность единиц

Полный оборот, совершенный за период T, равен 2π радиан. Следовательно, пройден радиан . Угловая скорость, которая описывает количество угловых единиц, пройденных за единицу времени, является обратной, поскольку частота f является обратной по отношению к периоду. Другими словами:
Т2π{\ displaystyle {\ frac {T} {2 \ pi}}}ωзнак равно2πТзнак равно2πж{\ displaystyle \ omega = {\ frac {2 \ pi} {T}} = 2 \ pi f}

В международной системе единиц время выражается в секундах, а частота — в герцах .

Мы выводим эквивалентность между скоростью вращения в оборотах в минуту и ​​угловой скоростью в радианах в секунду.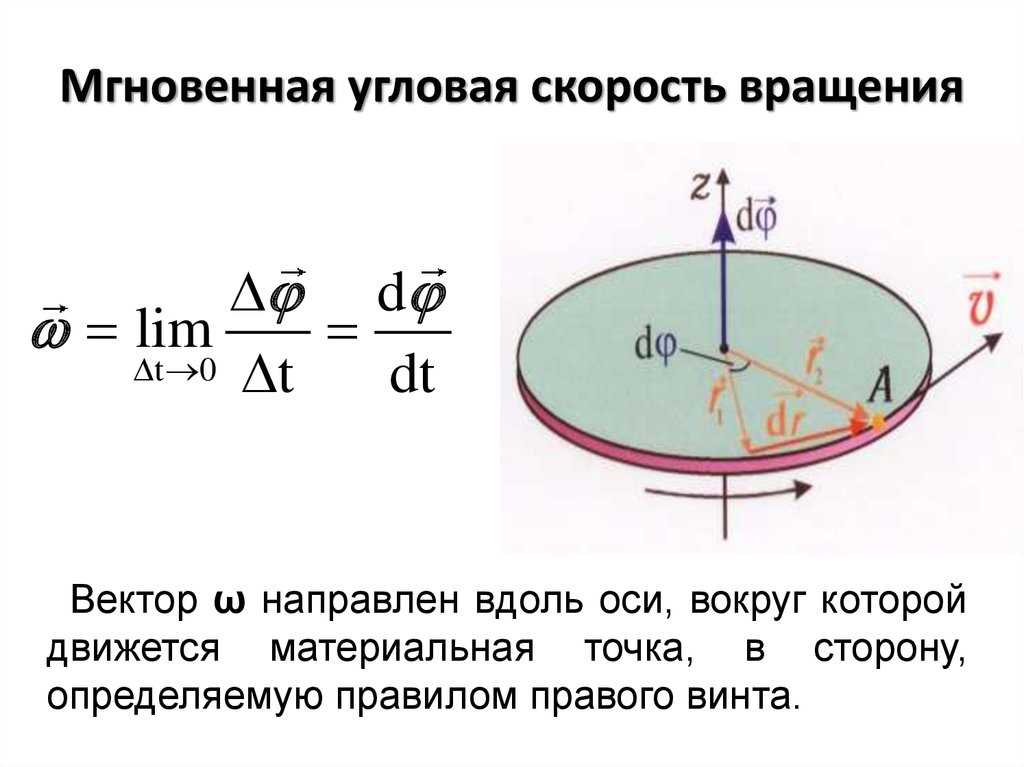 {- 1}}это размерность частоты .

Поскольку углы являются безразмерными величинами, их можно передать просто в с ^-1, но этого следует избегать, если единица измерения угла не является совершенно ясной.

Вектор угловой скорости

Иногда используется вектор угловой скорости . Это вектор:
ω→{\ displaystyle {\ vec {\ omega}}}

• перпендикулярно плоскости вращения;
• ориентированы так, чтобы движение было в положительном направлении, обычно задаваемом правилом правой руки  ;
• норма которого равна ω .

Таким образом, вектор угловой скорости определяет как ось, вокруг которой вращается объект, так и скорость его вращения. Это не совсем вектор, а псевдовектор, поскольку симметричное в зеркале инвертировано.

Использование вектора угловой скорости позволяет применять методы вычисления вектора к объектам, вращающимся относительно друг друга.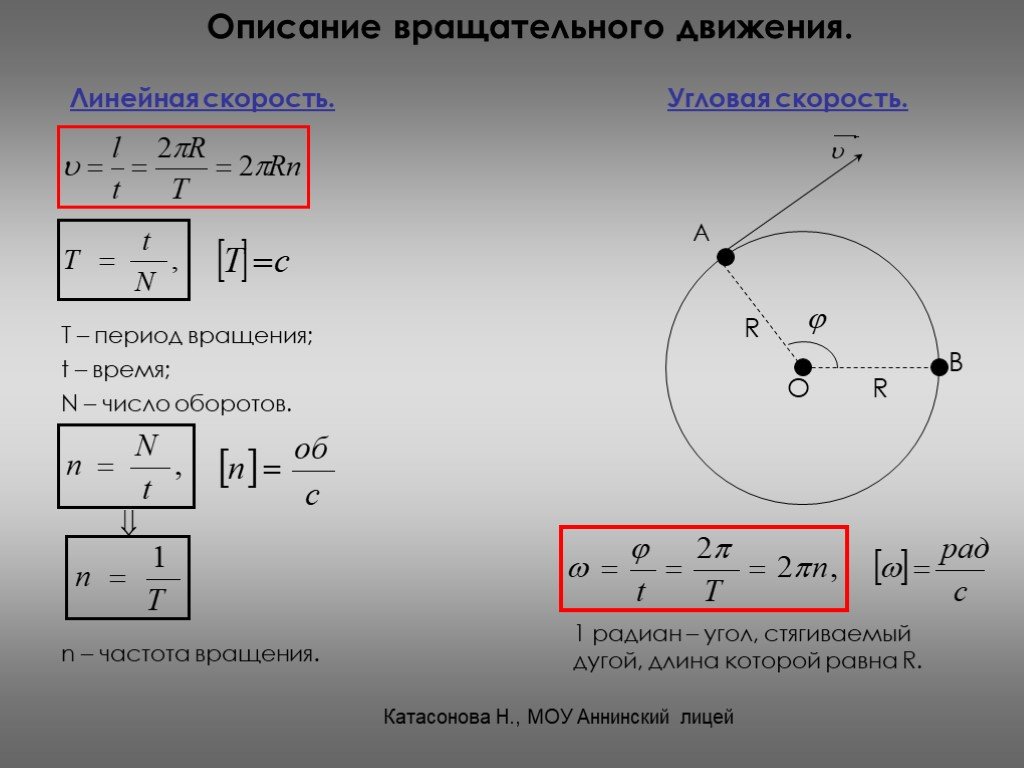

Он позволяет составлять угловые скорости путем сложения векторов и вычислять линейные скорости из угловых скоростей.

Циркулярный перевод:

В объекте, вращающемся вокруг опоры, который сам вращается, сложение векторов угловой скорости дает движение объекта.

Если два вектора угловой скорости направлены в одном направлении, но в противоположном направлении, их сложение дает нулевой вектор. Объект описывает круг, не меняя ориентации, в круговом поступательном движении .

Примечания и ссылки

1. ↑ Dubesset 2000, стр.  4 ( онлайн ), стр.  122 ( онлайн ).
2. ↑ Dubesset 2000, стр.  104.
3. ↑ «На практике символы rad и sr используются по мере необходимости», Международное бюро мер и весов, Единицы со специальными названиями и специальными символами .

Смотрите также

Библиография

 : документ, использованный в качестве источника для этой статьи.

• Ричард Тайлле, Лоик Злодей и Паскаль Февр, Физический словарь, Брюссель, Де Бок ,2013, 3 ^е  изд. , Х-899  с. ( ISBN  978-2-8041-7554-2, читать онлайн ) :
  • п.  561 , «Пульсация» ,
  • п.  723 «Угловая скорость» ,
  • [ Дик. Phys. , изд. 2008  (страница консультации по 23 июля 2014)] ( ( ISBN  978-2-8041-5688-6 ) (уведомление BnF п ^о  FRBNF41256105 ), соответственно. P.  405 и стр.  523 .
• Мишель Дюбессе, Руководство Международной системы единиц: лексика и преобразования, Париж, Technip, колл.  «Публикации Французского нефтяного института  »,2000 г., 169  с. ( ISBN  2-7108-0762-9, уведомление BnF п ^о  FRBNF37624276, читать онлайн )

Статьи по Теме

• Момент (механический)
• Вектор угловой скорости
• Аналогия между вращением и перемещением

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Угловая скорость

В физике угловая скорость определяется как скорость изменения углового смещения и является векторной величиной (точнее, псевдовектором), задающей угловую скорость объекта и ось, вокруг которой объект вращается . Единицей угловой скорости в СИ является радиан в секунду, хотя она может измеряться и в других единицах, таких как градусы в секунду, градусы в час и т. д. Угловая скорость обычно обозначается символом омега (ω, редко Ω).

Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно определяется правилом правой руки.[1]

Угловая скорость частицы
Частица в двух измерениях
Угловая скорость частицы в точке P относительно начала координат O определяется перпендикулярной составляющей вектора скорости v.
Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение. Направление псевдовектора угловой скорости будет вдоль оси вращения; в этом случае (вращение против часовой стрелки) вектор указывает вверх.

Угловая скорость частицы измеряется вокруг или относительно точки, называемой началом координат. Как показано на диаграмме (с углами ɸ и θ в радианах), если провести линию от начала координат (O) к частице (P), то скорость (v) частицы имеет составляющую по радиусу (радиальная составляющая v‖) и составляющая, перпендикулярная радиусу (поперечно-радиальная составляющая v⊥). При отсутствии радиальной составляющей частица движется по окружности, а при отсутствии перпендикулярной к радиусу составляющей частица движется по прямой через начало координат.

Радиальное движение не приводит к изменению направления частицы относительно начала координат, поэтому при определении угловой скорости можно пренебречь радиальной составляющей. Следовательно, вращение полностью производится перпендикулярным движением вокруг начала координат, и угловая скорость полностью определяется этой составляющей.

В двух измерениях угловая скорость ω определяется выражением

\( \omega = \frac{d\phi}{dt} \)

Это связано с поперечно-радиальной (тангенциальной) скоростью соотношением:[1]

\( \mathrm{v}_\perp=r\,\frac{d\phi}{dt} \)

Явная формула для v⊥ через v и θ:

\mathrm{v }_\perp=|\mathrm{\mathbf{v}}|\,\sin(\theta). \)

Объединение приведенных выше уравнений дает формулу для ω:

\( \omega=\frac{|\mathrm{\mathbf{v}}|\sin(\theta)}{|\mathrm{\mathbf{ r}}|}. \)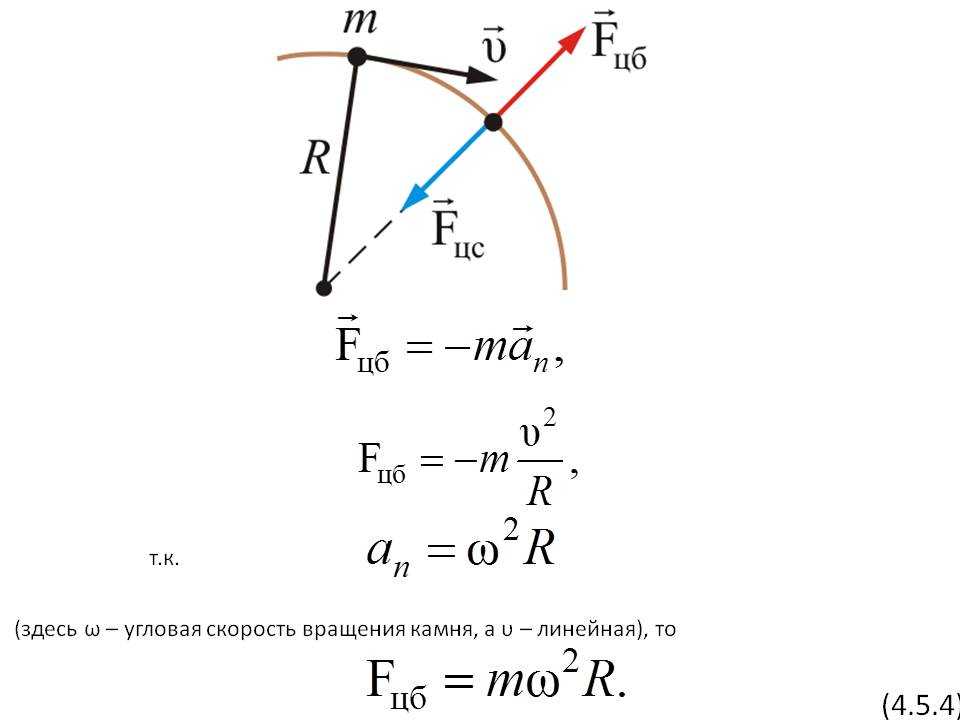

В двух измерениях угловая скорость является единственным числом, которое не имеет направления, но имеет смысл или ориентацию. В двух измерениях угловая скорость является псевдоскаляром, величиной, которая меняет свой знак при инверсии четности (например, если одна из осей перевернута или они переставлены местами). По соглашению принято положительное направление вращения в направлении оси у от оси х. Если четность инвертируется, а направление вращения нет, то меняется знак угловой скорости.
Частица в трех измерениях
См. также: Формулы Френе-Серре

В трех измерениях угловая скорость становится немного сложнее. Угловая скорость в этом случае обычно понимается как вектор или, точнее, как псевдовектор. Теперь у него есть не только величина, но и направление. Величина — это угловая скорость, а направление описывает ось вращения. Правило правой руки указывает положительное направление псевдовектора угловой скорости.

Будучи \vec u унитарным вектором относительно оси мгновенного вращения, так что от вершины вектора вращение против часовой стрелки, вектор угловой скорости \vec \omega может быть определен как:

\( \vec \omega = \frac{d\theta}{dt}\cdot\vec u \)

Как и в двумерном случае, частица будет иметь составляющую своей скорости вдоль радиуса от начала координат до частицы, и другой компонент, перпендикулярный этому радиусу.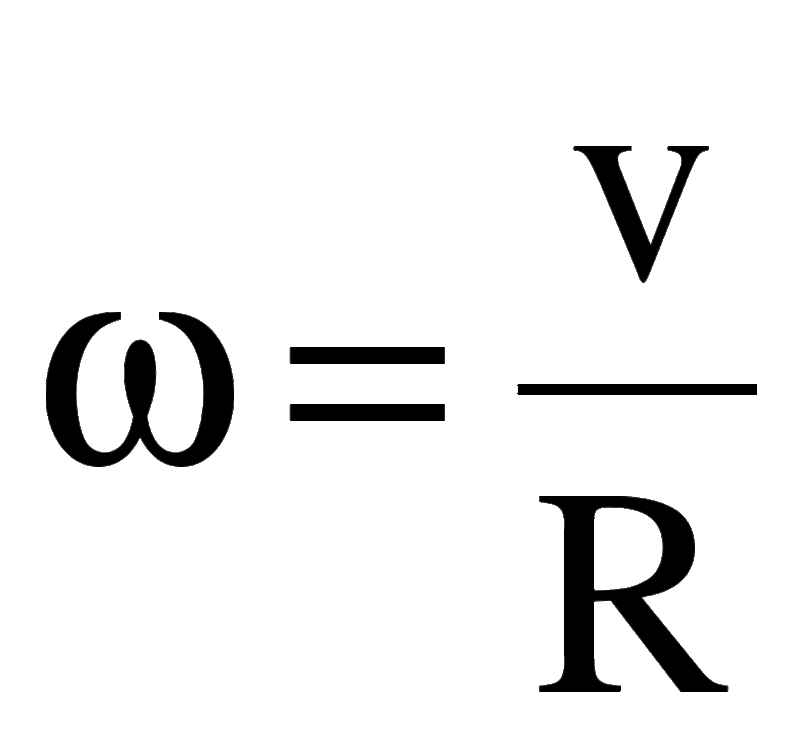 Комбинация исходной точки и перпендикулярной составляющей скорости определяет плоскость вращения, в которой поведение частицы (на данный момент) выглядит точно так же, как в двумерном случае. Ось вращения тогда является линией, нормальной к этой плоскости, и эта ось определяет направление псевдовектора угловой скорости, в то время как величина совпадает с псевдоскалярным значением, найденным в 2-мерном случае. Используя единичный вектор \vec u, определенный ранее, вектор угловой скорости можно записать так же, как и для двух измерений:2} \)

Сложение векторов угловых скоростей

Операцию сложения векторов угловых скоростей можно определить с помощью композиции движений.

Если точка вращается с \( \omega_2 \) в системе отсчета \( F_2 \), которая вращается с угловой скоростью \omega_1 относительно внешней системы отсчета F_1, мы можем определить добавление \( \omega_1 + \omega_2 \) как вектор угловой скорости точки относительно \( F_1. 2 + … \)

Композиция вращений не является коммутативной, но когда они являются бесконечно малыми вращениями, можно использовать первое приближение предыдущего ряда и \( (I+W_1\cdot dt)(I+W_2 \cdot dt)=(I+ W_2.dt)(I+W_1\cdot dt) \) , и поэтому\( \omega_1 + \omega_2 = \omega_2 + \omega_1 \)
Вращающиеся системы отсчета

Для данной вращающейся системы отсчета, состоящей из трех унитарных векторов, все три должны иметь одинаковую угловую скорость в любой момент времени. В такой системе отсчета каждый вектор является частным случаем предыдущего случая (движущаяся частица), в котором модуль вектора постоянен.

Хотя это всего лишь частный случай предыдущего, он очень важен из-за его связи с изучением твердого тела, и для этого случая были разработаны специальные инструменты. Есть два возможных способа описать угловую скорость вращающейся системы отсчета. Вектор угловой скорости и тензор угловой скорости. Обе сущности связаны, и их можно вычислить друг из друга.
Вектор угловой скорости для системы отсчета

Он определяется как угловая скорость каждого из векторов системы отсчета в соответствии с общим определением.

Из теоремы Эйлера о вращении известно, что для вращающейся системы отсчета существует мгновенная ось вращения в любой момент времени. В случае рамы вектор угловой скорости проходит над мгновенной осью вращения.

Любое поперечное сечение плоскости, перпендикулярной этой оси, должно вести себя как двумерное вращение. Таким образом, величина вектора угловой скорости в данный момент времени t согласуется с двухмерным случаем.

Угловая скорость — это вектор, определяющий операцию сложения. Компоненты могут быть рассчитаны из производных параметров, определяющих подвижную систему отсчета (углы Эйлера или матрицы поворота)
Сложение векторов угловой скорости в кадрах
Схематическое построение сложения векторов угловых скоростей для вращающихся систем отсчета

Как и в общем случае, операция сложения векторов угловых скоростей может быть определена с помощью композиции движения. В случае вращающихся кадров композиция движения проще, чем в общем случае, поскольку конечная матрица всегда является произведением матриц вращения.

Как и в общем случае, сложение коммутативно \( \omega_1 + \omega_2 = \omega_2 + \omega_1 \) 92} \), и поэтому \( \vec \omega = \vec {e}_1\times \dot{\vec{e}}_1 = \vec {e}_2\times \dot{\vec{e}} _2 = \vec {e}_3\times \dot{\vec{e}}_3. \)

Поскольку столбцы матрицы репера являются компонентами его векторов, это позволяет также вычислить \omega из матрица репера и ее производная.
Компоненты из углов Эйлера
Диаграмма, показывающая систему Эйлера, выделенную зеленым цветом

Компоненты псевдовектора угловой скорости были впервые рассчитаны Леонардом Эйлером с использованием его углов Эйлера и промежуточной системы координат, составленной из промежуточных систем построения:

Одна ось системы отсчета (ось прецессии)
Линия узлов подвижной системы отсчета относительно системы отсчета (ось нутации)
Одна ось подвижной системы отсчета (собственная ось вращения)

Эйлер доказал, что проекции псевдовектора угловой скорости по этим трем осям являются производными соответствующего ему угла (что эквивалентно разложению мгновенного вращения на три мгновенных эйлеровых поворота) . Следовательно[2]:

\( \vec \omega = \dot\alpha \bold u_1 +\dot\beta \bold u_2 +\dot\gamma \bold u_3 \)

Этот базис не ортонормирован и его сложно использовать, но теперь вектор скорости можно изменить на фиксированную или подвижную систему отсчета, просто заменив базы. Например, переход на мобильную рамку:

\( \vec \omega = (\dot\alpha\sin\beta\sin\gamma+\dot\beta\cos\gamma){\bold I} +(\dot\ альфа\sin\beta\cos\gamma-\dot\beta\sin\gamma){\bold J} +(\dot\alpha\cos\beta+\dot\gamma){\bold K}, \)

где IJK — орты для системы отсчета, закрепленной в движущемся теле. Этот пример был сделан с использованием соглашения Z-X-Z для углов Эйлера [3].
Компоненты бесконечно малых матриц вращения

Компоненты вектора угловой скорости могут быть рассчитаны из бесконечно малых вращений (если доступны) следующим образом:

Поскольку любая матрица вращения имеет единственное действительное собственное значение, равное +1, это собственное значение показывает ось вращения .
Его модуль можно вывести из значения бесконечно малого вращения.

Тензор угловой скорости
См. также: Кососимметричная матрица

Может быть введена из матриц вращения. Любой вектор \vec r, который вращается вокруг оси с вектором угловой скорости \vec \omega (как определено ранее), удовлетворяет условию:

\( \frac {d \vec r(t)} {dt} = \vec{\omega } \times\vec{r} \)

Мы можем ввести здесь тензор угловой скорости, связанный с угловой скоростью \omega:

\( W(t) = \begin{pmatrix} 0 & -\omega_z(t) & \omega_y(t) \\ \omega_z(t) & 0 & -\omega_x(t) \\ -\omega_y(t) & \omega_x(t) & 0 \\ \end{pmatrix} \)

Этот тензор W(t) будет действовать так, как если бы он был оператором (\vec \omega \times):

\( \vec \omega(t) \times \vec{r}(t) = W(t ) \vec{r}(t) \)

Зная матрицу ориентации A(t) системы отсчета, мы можем получить ее тензор мгновенной угловой скорости W следующим образом.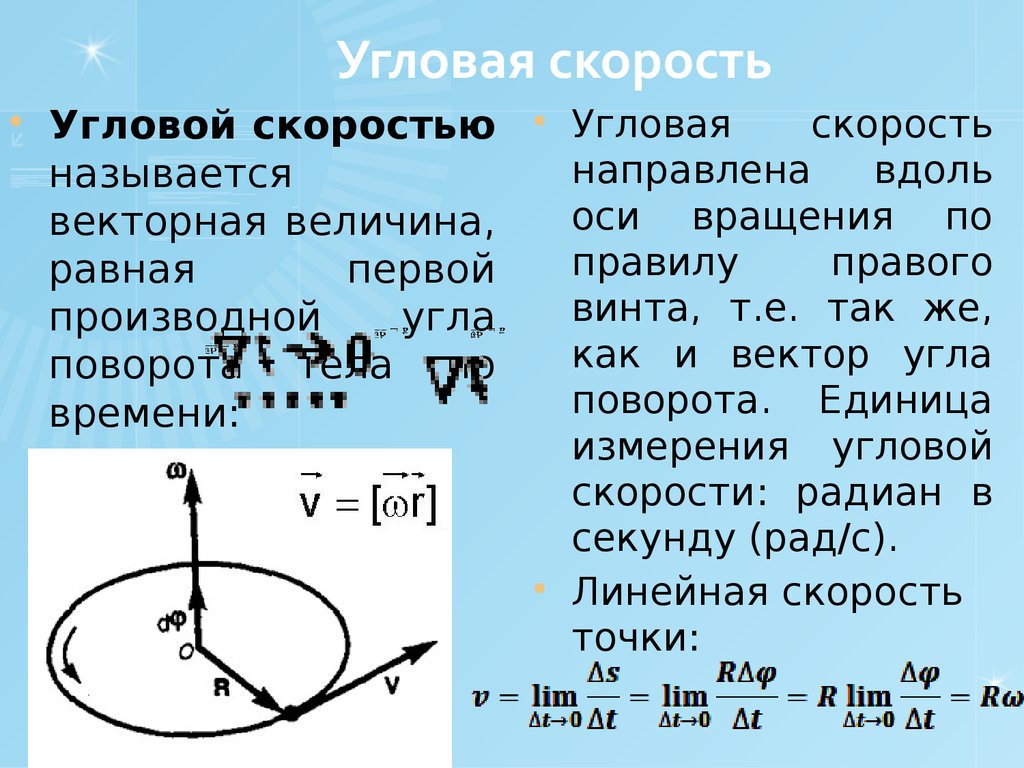 Мы знаем, что:

\( \frac {d \vec r(t)} {dt} = W \cdot \vec{r} \)

Поскольку угловая скорость должна быть одинаковой для трех векторов вращающейся системы отсчета , если у нас есть матрица A(t), столбцы которой являются векторами репера, мы можем написать для трех векторов в целом: 9{-1}(t) \)

Свойства тензоров угловых скоростей
См. также: Бесконечно малое вращение

В общем случае угловая скорость в n-мерном пространстве является производной по времени от тензора углового смещения, который является кососимметричным тензором второго ранга.

Этот тензор W будет иметь n(n-1)/2 независимых компонентов, и это число является размерностью алгебры Ли группы Ли вращений n-мерного внутреннего пространства произведения.[4]
Экспонента W

В трех измерениях угловая скорость может быть представлена ​​псевдовектором, потому что тензоры второго ранга двойственны псевдовекторам в трех измерениях. {W \cdot t} \) \) 9t \)

Таким образом, W является отрицательным значением своей транспонированной матрицы, что означает, что она является кососимметричной матрицей.
Двойственность относительно вектора скорости

Тензор представляет собой матрицу со следующей структурой:

\( W(t) = \begin{pmatrix} 0 & -\omega_z(t) & \omega_y(t) \\ \omega_z(t ) & 0 & -\omega_x(t) \\ -\omega_y(t) & \omega_x(t) & 0 \\ \end{pmatrix} \)

Поскольку это кососимметричная матрица, она имеет двойственный вектор Ходжа который в точности совпадает с предыдущим вектором угловой скорости \( \vec \omega \):

\( \boldsymbol\omega=[\omega_x,\omega_y,\omega_z] \)

Бескоординатное описание

В любой момент времени t тензор угловой скорости представляет собой линейное отображение между векторами положения \( \ mathbf{r}(t) \) и их векторы скоростей \( \mathbf{v}(t) \) твердого тела, вращающегося вокруг начала координат:

\( \mathbf{v} = W\mathbf{r} \)

, где мы опустили параметр t и рассматриваем \( \mathbf{v} \) и \( \mathbf{r} \) как элементы одного и того же трехмерного евклидова векторного пространства V.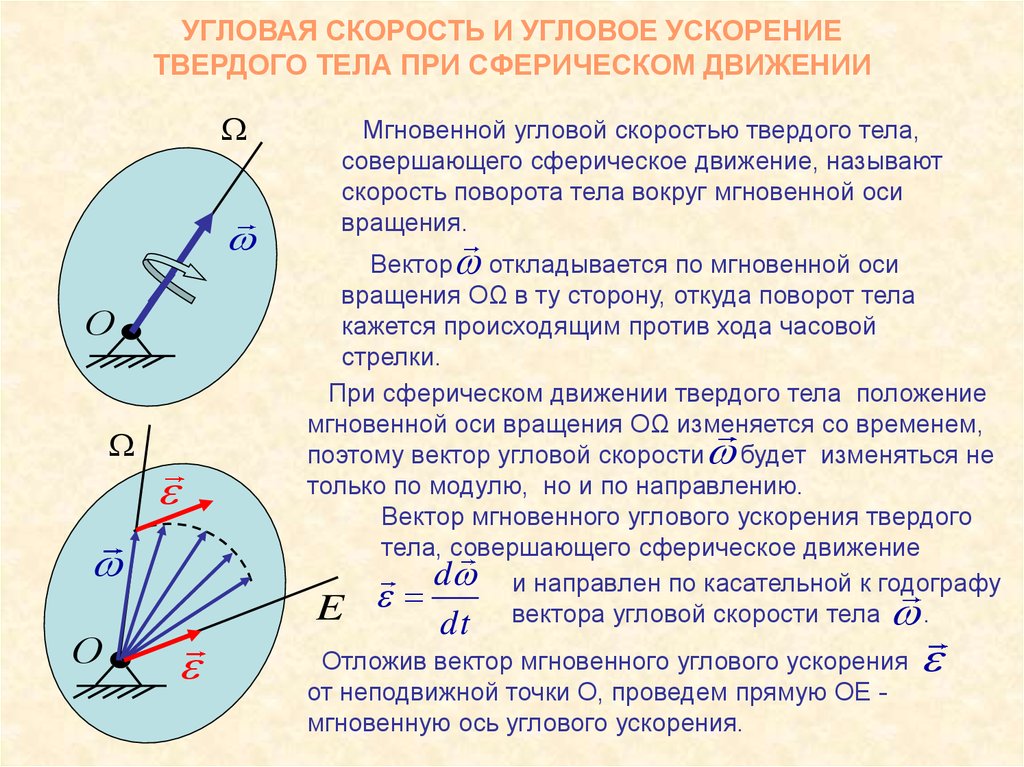 9* \клин \mathbf{r} \клин \mathbf{s}) = * (\omega \клин \mathbf{r} \клин \mathbf{s}) = *(\omega \клин \mathbf{r}) \ cdot \mathbf{s} = (\omega \times \mathbf{r}) \cdot \mathbf{s} \)

, где

\( \omega \times \mathbf{r} := *(\omega \ клин \mathbf{r}) \)

по определению.

Поскольку \( \mathbf{s} \) произвольный вектор, из невырожденности скалярного произведения следует

\( W\mathbf{r} = \omega \times \mathbf{r} \)

Угловая скорость как векторное поле

Для тензора угловой скорости скорости отображаются в положения, это векторное поле. В частности, это векторное поле является векторным полем Киллинга, принадлежащим элементу алгебры Ли so(3) трехмерной группы вращений SO(3). Этот элемент so(3) также можно рассматривать как вектор угловой скорости.
Соображения по жесткому кузову
См. также: обозначения осей
Положение точки P, расположенной в твердом теле (показано синим цветом).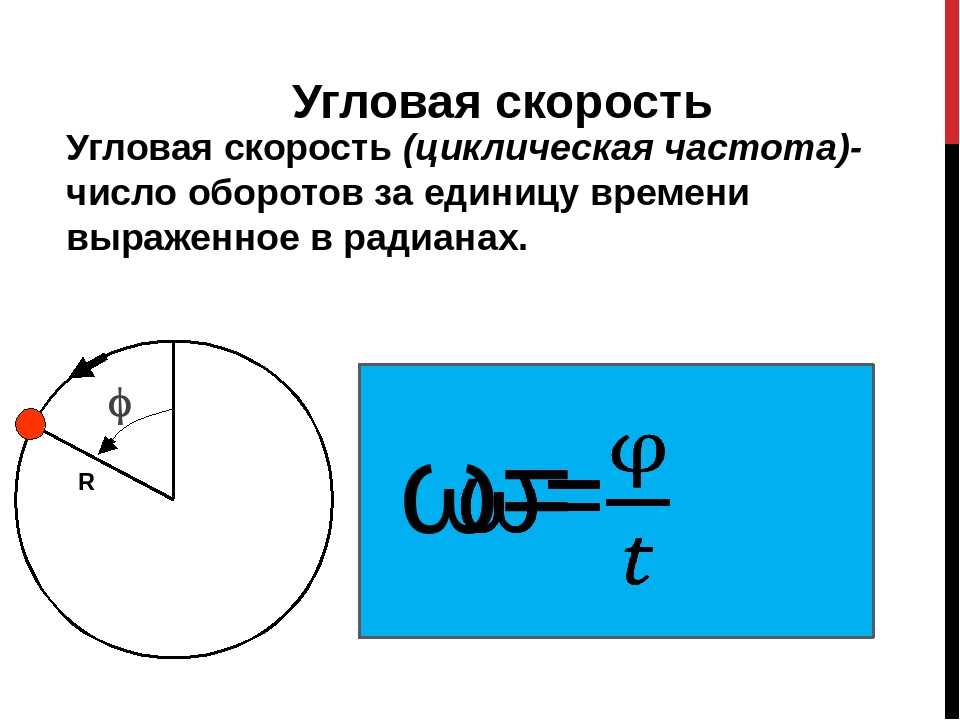 Ri — положение относительно лабораторной рамы с центром в точке O, а ri — положение относительно жесткого корпуса с центром в точке O’. Исходная точка каркаса твердого тела находится в позиции вектора R от лабораторного каркаса.

Те же уравнения для угловой скорости можно получить, рассуждая о вращающемся твердом теле. Здесь не предполагается, что твердое тело вращается вокруг начала координат. Вместо этого можно предположить вращение вокруг произвольной точки, движущейся с линейной скоростью V(t) в каждый момент времени.

Для получения уравнений удобно представить твердое тело, прикрепленное к рамам, и рассмотреть систему координат, неподвижную относительно твердого тела. Затем мы изучим преобразования координат между этой координатой и фиксированной «лабораторной» системой.

Как показано на рисунке справа, начало лабораторной системы находится в точке O, начало системы твердого тела — в точке O’, а вектор от O к O’ — это R. Частица (i) в твердом теле находится в точке P, а положение вектора этой частицы в лабораторной системе координат равно Ri, а в системе тела — в положении ri. Видно, что положение частицы можно записать:

\( \mathbf{R}_i=\mathbf{R}+\mathbf{r}_i \)

Определяющей характеристикой твердого тела является то, что расстояние между любыми двумя точками твердого тела не меняется во времени. Это означает, что длина вектора \(\mathbf{r}_i \) неизменна. По теореме Эйлера о вращении мы можем заменить вектор \mathbf{r}_i на \mathcal{R}\mathbf{r}_{io}, где \mathcal{R} — матрица вращения 3×3, а \( \mathbf{r} _{io} \) — это положение частицы в некоторый фиксированный момент времени, скажем, t=0. Эта замена полезна, потому что теперь во времени меняется только матрица вращения \( \mathcal{R} \), а не опорный вектор \( \mathbf{r}_{io} \), как твердое тело вращается вокруг точки О’. Кроме того, поскольку три столбца матрицы вращения представляют собой три версора системы отсчета, вращающейся вместе с твердым телом, теперь становится видимым любое вращение вокруг любой оси, в то время как вектор \(\mathbf{r}_i \) не будет вращаться если бы ось вращения была ей параллельна, и, следовательно, она описывала бы только вращение вокруг оси, перпендикулярной ей (т. е. не видела бы параллельную ей составляющую псевдовектора угловой скорости, а позволяла бы только вычислять составляющую перпендикулярно ему). Положение частицы теперь записывается как: 9Т\) — предыдущий тензор угловой скорости.

Можно доказать, что это кососимметричная матрица, поэтому мы можем взять ее двойственный, чтобы получить трехмерный псевдовектор, который точно совпадает с предыдущим вектором угловой скорости \( \vec \omega \):

\( \boldsymbol\omega =[\omega_x,\omega_y,\omega_z] \)

Подставив ω вместо W в вышеприведенное выражение скорости и заменив матричное умножение эквивалентным перекрестным произведением:

\( \mathbf{V}_i=\mathbf{V }+\mathbf\omega\times\mathbf{r}_i. \)

Можно видеть, что скорость точки в твердом теле можно разделить на два слагаемых – скорость точки отсчета, закрепленной в твердом теле, плюс член перекрестного произведения, включающий угловую скорость частицы относительно ориентир. Эта угловая скорость является «спиновой» угловой скоростью твердого тела в отличие от угловой скорости точки отсчета O’ относительно начала координат O.
Согласованность

Мы предположили, что твердое тело вращается вокруг произвольной точки. Мы должны доказать, что определенная ранее угловая скорость не зависит от выбора начала координат, а это означает, что угловая скорость является внутренним свойством вращающегося твердого тела.
Доказательство независимости угловой скорости от выбора начала координат

См. график справа: Начало лабораторной системы отсчета — O, а O1 и O2 — две фиксированные точки на твердом теле, скорость которых равна \( \mathbf{v} _1 \) и \(\mathbf{v}_2 \) соответственно. Предположим, что угловая скорость относительно O1 и O2 равна \(\boldsymbol{\omega}_1 \) и \(\boldsymbol{\omega}_2 \) соответственно. Поскольку точки P и O2 имеют только одну скорость,

\( \mathbf{v}_1 + \boldsymbol{\omega}_1\times\mathbf{r}_1 = \mathbf{v}_2 + \boldsymbol{\omega} _2\раз\mathbf{r}_2 \)

\( \mathbf{v}_2 = \mathbf{v}_1 + \boldsymbol{\omega}_1\times\mathbf{r} = \mathbf{v}_1 + \boldsymbol{\omega}_1\times ( \mathbf{r}_1 — \mathbf{r}_2).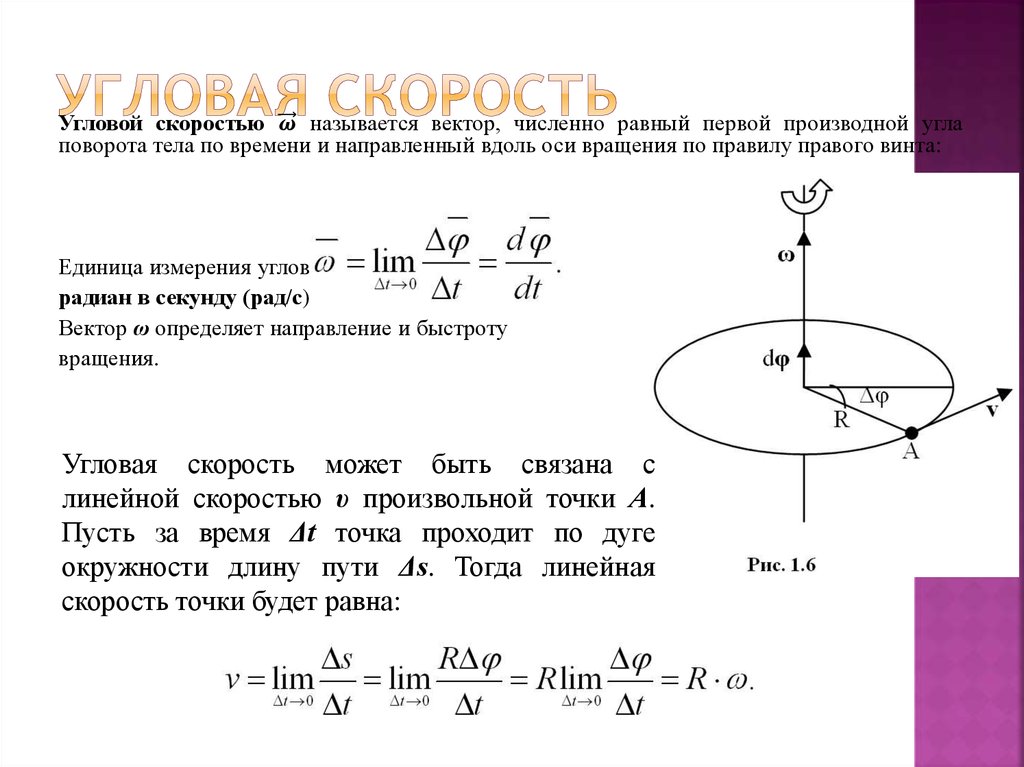 r}_2=0. \)

Поскольку точка P (и, следовательно, \( \mathbf{r}_2 \)) ) \) произвольна, отсюда следует, что

\( \boldsymbol{\omega}_1 = \boldsymbol {\omega}_2 . \)

Если исходной точкой является мгновенная ось вращения, выражение скорости точки в твердом теле будет иметь только член угловой скорости. Это связано с тем, что скорость мгновенной оси вращения равна нулю. Примером мгновенной оси вращения является дверная петля. Другим примером является точка контакта чисто катящегося сферического твердого тела. 9Вращения и угловой момент на странице классической механики веб-сайта Джона Баэза, особенно вопросы 1 и 2.

Саймон, Кейт (1971). Механика. Аддисон-Уэсли, Рединг, Массачусетс. ISBN 0-201-07392-7.

Ландау, Л.Д.; Лифшиц, Э. М. (1997). Механика. Баттерворт-Хайнеманн. ISBN 0-7506-2896-0.

Внешние ссылки
Найдите угловую скорость в Викисловаре, бесплатном словаре.

Учебник физики для колледжа Артур Лаланн Кимбалл (Угловая скорость частицы)

Энциклопедия физики

Получено с «http://en.wikipedia.org/»
Весь текст доступен на условиях лицензии GNU Free Documentation License

Home — Hellenica World

Определение угловой скорости в физике.

(существительное)

Векторная величина, описывающая круговое движение объекта; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.

(существительное)

Векторная величина, описывающая движение объекта по окружности; его величина равна угловой скорости ($\omega$) частицы, а направление перпендикулярно плоскости ее кругового движения.

• Угол вращения и угловая скорость

  • Хотя угол сам по себе не является векторной величиной, угловая скорость является вектором.
  • Угловое ускорение дает скорость изменения угловой скорость .
  • Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
  • Объект вращается с угловой скоростью равной $\frac{v}{r}$.
  • Направление угловой скорости будет вдоль оси вращения.

• Угловая скорость, Омега

  • Единицами для угловой скорости являются радианы в секунду (рад/с).
  • Угловая Скорость ω аналогична линейной Скорость v.
  • Автомобиль, движущийся вправо со скоростью v, имеет шину, вращающуюся с угловой скоростью ω.
  • Большая угловая скорость для шины означает большую скорость для автомобиля.
  • Изучите скорость вращения объекта на основе угловой скорости

• Угловое ускорение, Альфа

  • Угловое ускорение есть скорость изменения угловой скорости , математически выраженная как $\alpha = \Delta \omega/\Delta t$ .
  • Угловое ускорение это скорость изменения угловой скорости .
  • Угловой ускорение определяется как скорость изменения угловой скорости .
  • , где $\Delta\omega$ — изменение угловой скорости , а $\Delta t$ — изменение во времени.
  • Тангенциальное ускорение at напрямую связано с угловым ускорением и связано с увеличением или уменьшением скорости (но не ее направления).

• Вращательная кинетическая энергия: работа, энергия и мощность

  • где $\omega$ — угловая скорость , а $I$ — момент инерции вокруг оси вращения.
  • Мгновенная мощность тела с угловым ускорением равна произведению крутящего момента на угловую скорость : $P = \tau \omega$.
  • Во вращающейся системе момент инерции играет роль массы, а угловая скорость играет роль линейной скорости .
  • Поскольку период Земли составляет около 23,93 часа, она имеет угловую скорость 7,29×10-5 рад/с.
  • Дополнительное трение двух глобальных приливных волн создает энергию физическим образом, бесконечно мало замедляя угловую скорость Земли.

• Постоянное угловое ускорение

  • Постоянная угловая ускорение описывает отношения между угловой скорость , угол поворота и время.
  • Просто используя нашу интуицию, мы можем начать видеть взаимосвязь величин вращения, таких как θ (угол поворота), ω ( угловая скорость скорость ) и α ( угловая скорость ускорение).
  • Вращательное движение колеса аналогично тому факту, что большое поступательное ускорение мотоцикла дает большую конечную скорость , и пройденное расстояние также будет большим.
  • Точно так же кинематика вращательного движения описывает соотношения между углом поворота, угловой скоростью , угловым ускорением и временем.
  • Отношение угла поворота, углового скорости и углового ускорения к их эквивалентам в линейной кинематике

• Угловые и линейные величины

  • С ним связан тот же набор векторных величин, включая угловой скорость и угловой импульс.
  • Единицами измерения углового скорости являются радианы в секунду.
  • Точно так же, как существует угловая версия скорости , также существует угловая версия ускорения.
  • Как и в случае с линейным ускорением, угловое ускорение является изменением вектора угловой скорости .
  • Угловой Скорость может быть по часовой стрелке или против часовой стрелки.

• Угловые величины как векторы

  • Направление угловых величин, таких как угловая скорость и угловой импульс, определяется с помощью правила правой руки.
  • Угловой импульс и угловой скорость имеют как величину, так и направление и, следовательно, являются векторными величинами.
  • Вдоль этой оси можно определить направление углового импульса и скорости .
  • Правило правой руки можно использовать для определения направления углового импульса и угловой скорости .
  • Направление углового скорости размера ω и углового импульса L определяется как направление, в котором указывает большой палец правой руки, когда вы сгибаете пальцы в направлении вращения диска, как показано на рисунке.

• Связь между линейными и вращательными величинами

  • Иногда описание движения может быть проще с угловыми величинами, такими как угловая скорость , инерция вращения, крутящий момент и т. д.
  • Когда мы описываем равномерное круговое движение с точки зрения угловой скорости , противоречия нет.
  • Скорость (т.е. угловая скорость ) действительно постоянна.
  • Это первое преимущество описания равномерного кругового движения с точки зрения угловой скорости .
  • Второе преимущество состоит в том, что угловая скорость передает физический смысл вращения частицы в отличие от линейной скорости , которая указывает на поступательное движение.

• Вращательные столкновения

  • Когда объект массой m и со скоростью v сталкивается с другим объектом массой m2 и со скоростью v2, чистый импульс после столкновения, mv1f + mv2f, совпадает с импульсом до столкновения, mv1i + mv2i.
  • Для объектов с вращательной составляющей существует угловой момент импульсов.
  • Угловой момент математически определяется как L=Iω или L=rxp.
  • Объект, имеющий большую угловую скорость ω, например центрифуга, также имеет довольно большую угловой момент импульс.