Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)

События

Все события

Все анонсы

• Программа. I международная научно-техническая конф…
• Мастер класс по художественному мастерству…
• Заседание совета университета…
• Олимпиада по начертательной геометрии …
• Выставка «Геноцид в Гомельской области во время В…
• ЕДИ «Основные направления государственной политики…
• Приглашение на каток
• Финал осенней серии игр «ЧТО? ГДЕ? КОГДА?» среди с…
• Смотр-конкурс на лучшее праздничное Новогоднее и Р…
• Билеты на детское новогоднее представление и спект…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Программа. I международная научно-техническая конф…

Мастер класс по художественному мастерству…

Заседание совета университета…

Олимпиада по начертательной геометрии …

Новости

Университет

Международные связи

Спорт

Воспитательная работа

Жизнь студентов

Новости подразделений



• Университет

Новый номер газеты «Вести БелГУТа»
16 декабря 2022

• Воспитательная работа

Диалоговая площадка с Алексеем Талаем
16 декабря 2022

• Университет

75-летие Республиканского государственно-общественного объединения «Бе. ..
15 декабря 2022

• Воспитательная работа

Единый день информирования на ОАО «Мозырский домостроительный комбинат…
15 декабря 2022

• Университет

Итоги конкурсов Института современного образования «SmartSkills»…
15 декабря 2022

• Университет

Лица, имена, люди | Выпуск 2 | Старжинский Виктор Евгеньевич…
14 декабря 2022

• Студенческая жизнь

День студенческого самоуправления электротехнического факультета…
14 декабря 2022

• Университет

С юбилеем, уважаемый Федор Ефимович!
14 декабря 2022

• Университет

Итоги олимпиады ТОСВ-2022
13 декабря 2022

Другие новости

• Работы студентов БелГУТа на конкурсы к 160-летию Белорусской железной . ..
• Выпуск группы повышения квалификации по теме «Современные технологии у…
• К 160-летию белорусской магистрали
• Торжественный Пленум Гомельской городской оргструктуры Белорусское об…
• День открытых дверей военно-транспортного факультета…
• Республиканский научно-исторический семинар «Гомельщина. Вехи истории»…
• Дети из Донбасса приехали в Гомель на оздоровление…
• Финал евразийской лиги чемпионата мира по программированию…
• Доступная среда – инклюзивная Беларусь…
• Старт акции «Чудеса на Рождество»
• В Центре управления перевозками Белорусской железной дороги…

КУДА ПОСТУПАТЬ

Все факультеты

БелГУТ на Доске почета

Достижения университета

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

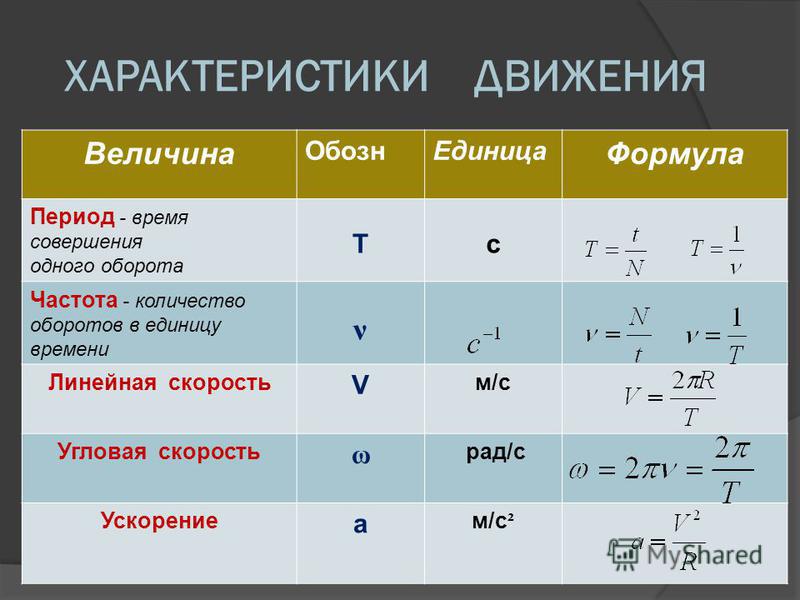
13 Вопросы для самоконтроля

Введение……………………………………………………………………	6
1. Кинематика поступательного и вращательного движения абсолютно твeрдого тела………………………………………………………………..	8
1.1. Поступательное движение…………………………………………….	8
1.2. Вращательное движение ………………………………………………	13
Вопросы для самоконтроля…………………………………………..	19
2. Динамика поступательного движения…………………………………….	21
2.1. Фундаментальные взаимодействия…………………………………..	21
2.2. Основные характеристики динамики Ньютона………………………	22
2.3. Закон инерции. Инерциальные системы отсчета…………………..	23
2.4. Масса и закон сохранения импульса…………………………………	24
2. 5. Второй закон Ньютона…………………………………………………	25
2.6. Третий закон Ньютона и закон сохранения импульса………………	26
2.7. Преобразования и принцип относительности Галилея	26
2.8. Основной закон динамики поступательного движения и закон сохранения импульса для системы материальных точек…………..	28
2.9. Некоторые силы, рассматриваемые в механике……………………..	32
2.10. Практическое применение законов Ньютона………………………	35
2.11. Движение тела с переменной массой ………………………………	36
Вопросы для самоконтроля…………………………………………..	37
3. Динамика вращательного движения твердого тела………………………	39
3.1. Основной закон динамики вращательного движения………………	39
3.2. Закон сохранения момента импульса…………………………………	45
Вопросы для самоконтроля……………………………………………	47
4. Работа. Мощность. Энергия………………………………………………..	48
4.1. Работа и мощность при поступательном движении ………………..	48
4.2. Работа и мощность при вращательном движении…………………..	50
4.3. Кинетическая энергия при поступательном движении……………..	51
4.4. Кинетическая энергия вращающегося тела…………………………. 5.2.1. Кинематические характеристики гармонического колебания…	63
5.2.2. Динамические характеристики гармонического колебания……	65
5.3. Маятник…………………………………………………………………	66
5.3.1. Математический маятник…………………………………………	66
5.3.2. Физический маятник………………………………………………	67
5.4. Сложение гармонических колебаний………………………………..	69
5.4.1. Сложение колебаний одной частоты, направленных вдоль одной прямой……….……….………………………………..….	70
5.4.2. Биения………………………………………………………………	71
5.4.3. Сложение взаимно перпендикулярных колебаний……………. .	72
5.5. Затухающие колебания………………………………………………..	76
5.6. Вынужденные колебания……………………………………………..	78
Вопросы для самоконтроля…………………………………………..	82
6. Упругие волны………………………………………………………………	85
6.1. Волновые процессы. Продольные и поперечные волны……………	85
6.2. Энергия упругих волн. Вектор Умова………………………………..	86
6.3. Уравнение бегущей волны. Фазовая скорость. Волновое уравне­ние…………………………………………………………………………	88
6.4. Принцип суперпозиции. Групповая скорость……………………….	90
6. 5. Интерференция волн…………………………………………………..	91
6.6. Стоячие волны…………………………………………………………	92
Вопросы для самоконтроля…………………………………………..	94
7. Молекулярная физика………………………………………………………	95
7.1. Предмет молекулярной физики и термодинамики. Статистический и термодинамический методы изучения макроскопических систем	95
7.2. Основные положения молекулярно-кинетической теории…………	96
7.3. Газообразное состояние вещества. Идеальный газ………………….	96
7.4. Параметры состояния идеального газа………………………………	97
7.5. Основное уравнение молекулярно-кинетической теории (урав­не­­­ние Клаузиуса) и следствия из него……………………………….	98
7.6. Закон Максвелла распределения молекул идеального газа по ско­­ростям и энергиям…………………………………………………….	103
7.7. Опыт Штерна………………………………………………………..	106
7.8. Идеальный газ в однородном поле тяготения. Барометрическая фор­мула. Распределение Больцмана…………………………………..	107
7.9. Число столкновений и средняя длина свободного пробега молекул	109
7.10. Явление переноса в газах…………………………………………….	110
7.11. Реальные газы…………………………………………………………	114
7.12. Уравнение Ван-дер-Ваальса…………………………………………	115
7. 13. Внутренняя энергия реального газа. Эффект Джоуля – Томсона…	119
7.14. Элементы механики жидкостей. Давление в жидкости и газе……	121
7.15. Уравнение Бернулли…………………………………………………	123
7.16. Движение тел в жидкостях и газах………………………………….	125
Вопросы для самоконтроля………………………………………..	127
8. Термодинамика……………………………………………………………..	130
8.1. Внутренняя энергия, работа и теплота……………………………….	130
8.2. Внутренняя энергия идеального газа. Степени свободы системы…	132
8.3. Работа и теплота……………………………………………………….	135
8.4. Первое начало термодинамики……………………………………….	138
8.5. Применение первого начала термодинамики к изопроцессам в иде­альном газе………………….………………………………………	140
8.6. Политропические процессы…………………………………………..	144
8.7. Тепловые двигатели и холодильные машины. Цикл Карно и его КПД………………………………………………………………….	147
8.8. Энтропия, ее статистическое толкование и связь с термо­динами­ческой вероятностью……………………………………………..……	150
8.9. Второе начало термодинамики……………………………………….	152
8.10. Применение второго начала термодинамики для определения из­ менения энтропии в процессах идеального газа……………. ..…..	153
8.11. Третье начало термодинамики, или теорема Нернста – Планка….	154
Вопросы для самоконтроля………………………………………….	155
Список литературы……………..…………………………………………	157

2$, потому что теперь у нас есть квадрат этого угла. Но так как единица измерения безразмерна, технически это не нужно. Это просто для удобства. Мы могли бы изобрести кучу других безразмерных единиц, чтобы помочь нам в бухгалтерии, но как только мы это сделали, мы должны сохранить их правильные мощности, иначе эти единицы просто бесполезны.

$\endgroup$

0

$\begingroup$

По определению, угловая скорость определяется как скорость изменения угла во времени, что приводит к уравнению $\omega = \Delta \theta / \Delta t$.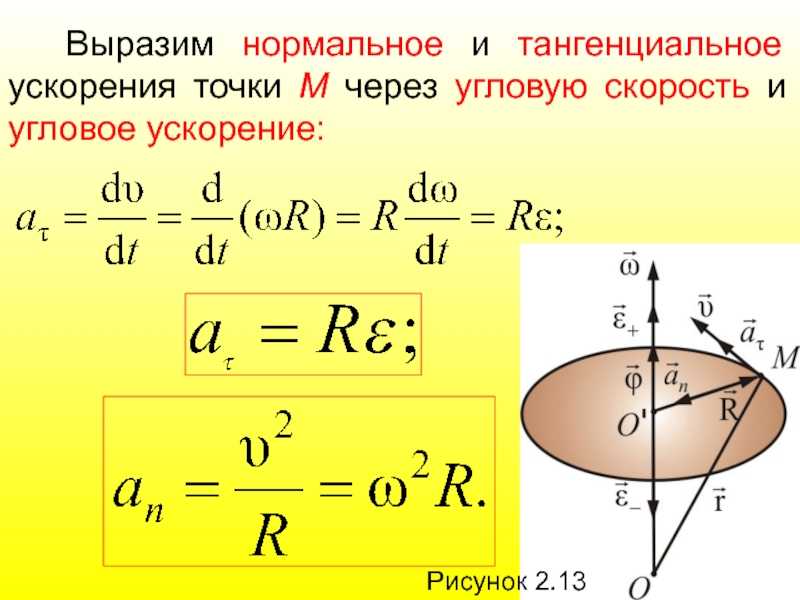 2$. 92}$.

$\endgroup$

$\begingroup$

Ваш вопрос немного похож на то, почему мое десятичное представление 1/3 никогда не заканчивается? Это потому, что мы выбрали базу 10, и если мы выберем другую базу (например, 9), мы можем сделать так, чтобы 1/3 заканчивалась (например, 0,3).

Единицы просто сравнивают количество с эталонным количеством, выбранным по соглашению. Я мог бы использовать секунды в качестве измерения расстояния, когда было понятно, что эталонное расстояние — это расстояние, которое проходит свет за секунду. В этом случае расстояние и время имеют одни и те же единицы измерения, и расстояние становится безразмерным, подобно показателю преломления.

Мы выбираем единицы измерения, чтобы отслеживать, какие ссылки мы использовали, отсюда и использование радов, даже если они безразмерны, а также почему мы используем метры вместо секунд для расстояния. Единицы гораздо более условны, чем мы часто их принимаем. Посмотрите на огромное количество систем единиц, используемых в электромагнетизме.

$\endgroup$

$\begingroup$

Физическая величина (плоский угол) — как описано Евклидом в его Элементах , датируемых примерно 2400 лет назад, — НЕ безразмерна. Равно как и радиан, определяемый как вершина угол кругового сектора, в котором длина дуги равна длине радиуса, часто встречается в известной конструкции (то, что мы видим, является частным углом, а не номером один). То, что сегодня называется «углом» (официально SI), на самом деле является числовым значением угла, когда этот угол выражается в радианах. Если тета — это угол (размерность: угол, A ), то «угол» в системе СИ равен тета/рад, т.е. мера угла в радианах: A / A 92 (но без уточняющих кавычек!).

Путаница, царящая в этом вопросе, проистекает из вездесущей формулы:
«тета» = (с/р). Поскольку правая сторона имеет размерность L / L = 1 , «угол» называется «безразмерным». На самом деле, LHS — это тета/рад (размерность: ×/× = ×1) — мера теты в радианах. Таким образом, физически правильное (и легко понимаемое) соотношение, вытекающее непосредственно из предложения 33 в Книге VI 9 Евклида0021 Элементы —is:

тета/рад = (s/r)

или, переставляя тета:

тета = (s/r) рад

В этих (физически правильных) соотношениях рад является естественным кажущаяся постоянная Природы (точно так же, как гравитационная постоянная, G, например) — это также оказывается полезным ВЫБОРОМ в качестве единицы .

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

10.1 Угловое ускорение – главы физики колледжа 1-17

10 Вращательное движение и угловой момент

Резюме

• Описать равномерное круговое движение.
• Объясните неравномерное круговое движение.
• Рассчитать угловое ускорение объекта.
• Соблюдайте связь между линейным и угловым ускорением.

Глава 6 Равномерное круговое движение и гравитация обсуждали только равномерное круговое движение, то есть движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Напомним, что угловая скорость[латекс]\boldsymbol{\omega}[/латекс] определялась как скорость изменения угла[латекс]\жирныйсимвол{\тета}:[/латекс]

[латекс]\boldsymbol{\omega\:=}[/латекс][латекс]\boldsymbol{\frac{\Delta\theta}{\Delta{t}}},[/latex]

, где[латекс]\жирныйсимвол{\тета}[/латекс] — угол поворота, как показано на рисунке 1.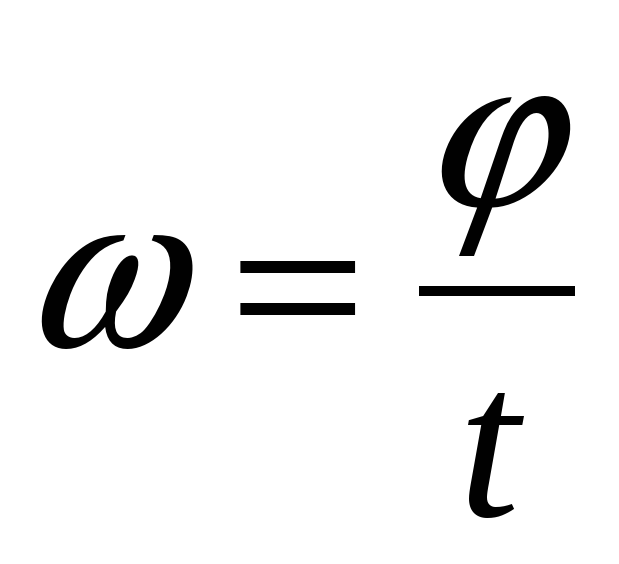 Связь между угловой скоростью[латекс]\жирныйсимвол{\омега}[/латекс] и линейной скоростью[латекс] \boldsymbol{v}[/latex] также был определен в главе 6.1 «Угол вращения и угловая скорость» как

.

[латекс]\boldsymbol{v=r\omega}[/латекс]

или

[латекс]\boldsymbol{\omega\:=}[/латекс][латекс]\boldsymbol{\frac{v}{r}},[/латекс]

, где[latex]\boldsymbol{r}[/latex] — радиус кривизны, также показанный на рисунке 1. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным

Рисунок 1. На этом рисунке показано равномерное круговое движение и некоторые его определяемые величины.

Угловая скорость непостоянна, когда фигурист тянет руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается при выключении. Во всех этих случаях есть угловое ускорение , при котором[латекс]\жирныйсимвол{\омега}[/латекс]изменяется. 2}.[/латекс]Если[латекс ]\boldsymbol{\omega}[/latex] увеличивается, тогда [латекс]\boldsymbol{\alpha}[/latex] положителен. Если [латекс]\boldsymbol{\omega}[/latex]убывает, то [латекс]\boldsymbol{\alpha}[/латекс]отрицательно. 92},[/latex]сколько времени нужно колесу, чтобы остановиться?

Стратегия для (a)

Угловое ускорение можно найти непосредственно из его определения в [latex]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}[/latex ]потому что заданы конечная угловая скорость и время. Мы видим, что [латекс]\boldsymbol{\Delta\omega}[/латекс]составляет 250 об/мин, а [латекс]\boldsymbol{\Delta{t}}[/латекс]составляет 5,00 с.

Решение для (а)

Вводя известные сведения в определение углового ускорения, получаем 92}[/latex]для углового ускорения нам нужно преобразовать[latex]\boldsymbol{\Delta\omega}[/latex]из об/мин в рад/с:

[latex]\begin{array}{lcl} \ boldsymbol{\Delta\omega} & \boldsymbol{=} & \boldsymbol{250\frac{\textbf{rev}}{\textbf{min}}\cdotp\frac{2\pi\textbf{rad}}{\ textbf{rev}}\cdotp\frac{1\textbf{ мин}}{60\textbf{ сек}}} \\ {} & \boldsymbol{=} & \boldsymbol{26,2\textbf{ рад.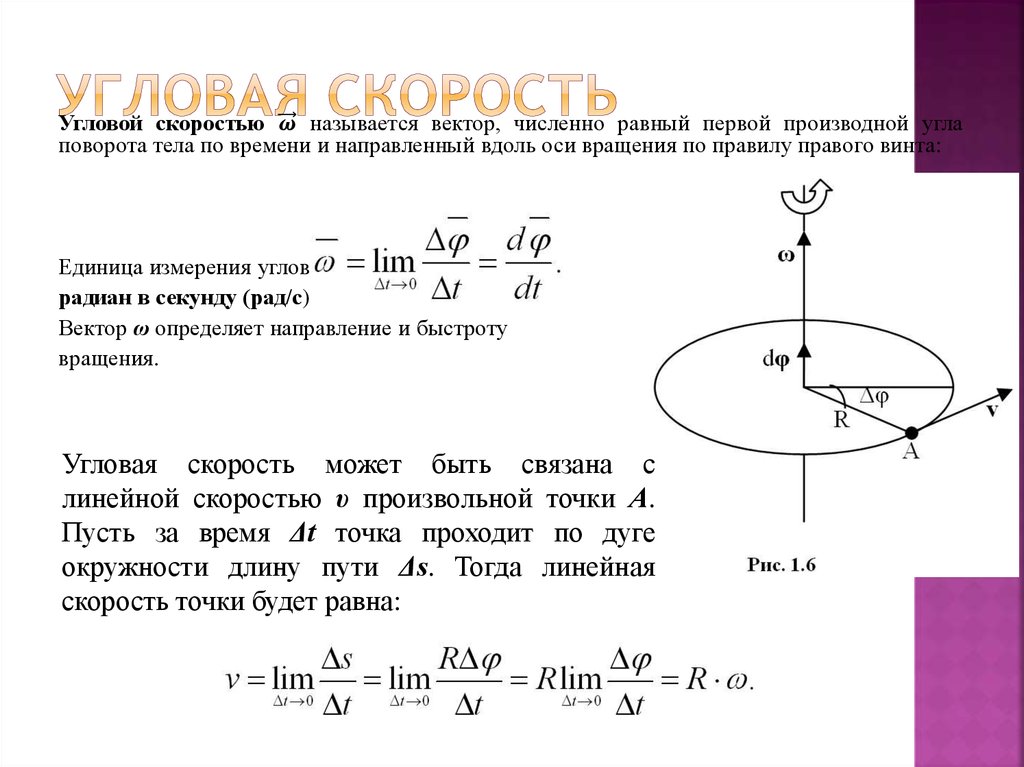 2}.[/ латекс] Таким образом, 92}} \\ {} & \boldsymbol{=} & \boldsymbol{0.300\textbf{ с.}} \end{array}[/latex]

Обсуждение

Обратите внимание, что угловое ускорение при вращении девушки колесо маленькое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.

Если бы велосипед в предыдущем примере стоял на колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение составляет по касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением[латекс]\жирныйсимвол{а_{\textbf{t}}}.[ /латекс]

Рисунок 2. При движении по окружности линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называют тангенциальным ускорением a _t .

Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Из главы 6 «Равномерное круговое движение и гравитация» мы знаем, что при круговом движении центростремительное ускорение,[latex]\boldsymbol{a_{\textbf{c}}},[/latex]относится к изменениям направления скорости, но не ее величины. . Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рис. 3. Таким образом, }}[/latex] перпендикулярны и независимы друг от друга. Тангенциальное ускорение[латекс]\boldsymbol{a_{\textbf{t}}}[/латекс]прямо связано с угловым ускорением[латекс]\жирныйсимвол{\альфа}[/латекс]и связано с увеличением или уменьшением скорость, но не ее направление.

Рис. 3. Центростремительное ускорение a _c возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.

Теперь мы можем найти точное соотношение между линейным ускорением[latex]\boldsymbol{a_{\textbf{t}}}[/latex]и угловым ускорением[latex]\boldsymbol{\alpha}.[/latex]Потому что линейное ускорение пропорциональна изменению модуля скорости, она определяется (как это было в главе 2 «Одномерная кинематика») равной

[латекс]\boldsymbol{a_{\textbf{t}}\:=}[/latex][латекс]\boldsymbol{\frac{\Delta{v}}{\Delta{t}}.}[/latex ]

Для кругового движения обратите внимание, что[latex]\boldsymbol{v=r\omega},[/latex], так что

[латекс]\boldsymbol{a _{\textbf{t}}\:=}[/latex][латекс]\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}.}[ /латекс]

Радиус[латекс]\boldsymbol{r}[/latex]постоянен для кругового движения, поэтому [латекс]\boldsymbol{\Delta(r\omega)=r(\Delta\omega)}. [/latex] Таким образом,

[латекс]\boldsymbol{a_{\textbf{t}}=r}[/latex][латекс]\boldsymbol{\frac{\Delta\omega}{\Delta{t}}.}[/latex]

По определению [латекс]\жирныйсимвол{\альфа=\фракция{\Delta\omega}{\Delta{t}}}.[/latex] Таким образом,

[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha},[/латекс]

или

[латекс]\boldsymbol{\alpha\:=}[/латекс][латекс]\boldsymbol{\frac{a_{\textbf{t}}}{r}.}[/latex]

Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении[latex]\boldsymbol{\alpha}.[/latex]

Пример 2: Расчет углового ускорения колеса мотоцикла

Мощный мотоцикл может разгоняться от 0 до 30,0 м/с (около 108 км/ч) за 4,20 с. 2.} \end{массив}[/latex]

Обсуждение

Радианы безразмерны и появляются в любом соотношении между угловыми и линейными величинами.

На данный момент мы определили три величины вращения — [латекс]\boldsymbol{\theta,\:\omega},[/latex]и [латекс]\boldsymbol{\alpha}.[/latex]Эти величины аналогичны поступательные величины[latex]\boldsymbol{x},\:\boldsymbol{v},[/latex]и[latex]\boldsymbol{a}.[/latex]В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.

Поворотный	Трансляционное	Отношения
[латекс]\boldsymbol{\theta}[/латекс]	[латекс]\boldsymbol{x}[/латекс]	[латекс] \boldsymbol{\theta=\frac{x}{r}}[/латекс]
[латекс]\boldsymbol{\omega}[/латекс]	[латекс]\boldsymbol{v}[/латекс]	[латекс]\boldsymbol{\omega=\frac{v}{r}}[/латекс]
[латекс]\boldsymbol{\alpha}[/латекс]	[латекс]\boldsymbol{a}[/латекс]	[латекс] \boldsymbol{\alpha=\frac{a_{\textbf{t}}}{r}}[/latex]
Таблица 1. Вращательные и поступательные величины.

СОЗДАНИЕ СОЕДИНЕНИЙ: ЭКСПЕРИМЕНТ ДЛЯ ДОМАШНИХ УСЛОВИЙ

Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу так, чтобы она была разогнута (выпрямлена). Используя другую ногу, начните вращать себя, отталкиваясь от земли. Прекратите использовать ногу, чтобы отталкиваться от земли, но позвольте стулу вращаться. От исходной точки, с которой вы начали, зарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков. Оцените величины этих величин.

ИССЛЕДОВАНИЯ PHET: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ

Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.

Рисунок 5.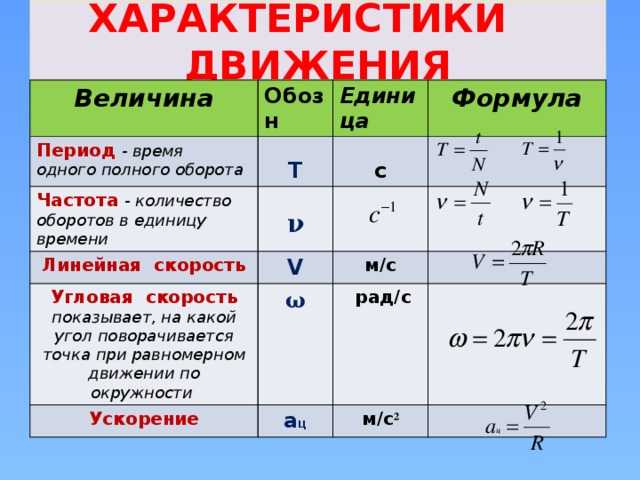 Революция божьей коровки

• Равномерное круговое движение – это движение с постоянной угловой скоростью[latex]\boldsymbol{\omega=\frac{\Delta\theta}{\Delta{t}}}.[/latex]
• При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t} }}.[/латекс]
• Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]\жирныйсимвол{а_{\textbf{t}}=\frac{\Delta{v}}{\Delta{t} }}.[/латекс]
• Для кругового движения обратите внимание, что[latex]\boldsymbol{v=r\omega},[/latex], так что

  [латекс]\boldsymbol{a _{\textbf{t}}\:=}[/latex][латекс]\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}}.[ /латекс]

• Радиус r постоянен для кругового движения, поэтому[латекс]\boldsymbol{\Delta(r\omega)=r\Delta\omega}.[/latex] Таким образом,

  [латекс]\boldsymbol{a_{\textbf{t}}=r}[/latex][латекс]\boldsymbol{\frac{\Delta\omega}{\Delta{t}}}.