Содержание
5. Мгновенная угловая скорость.
Мгновенная
угловая скорость равна первой производной
углового перемещения по времени:
(6)
При
равномерном вращении
,
тогда
(7)
6. Связь линейной и угловой скоростей.
Если продолжить
(3), то получим:
или
(8)
(9)
Вектор линейной
скоростисовпадает по направлению
с векторным произведением.
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора,
стоящего на первом месте в (9), к вектору,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора,
см. рис. 5.
Модуль
векторного произведения:
(10)
7. Модуль и направление углового ускорения.
При
вращении за время
угловая скорость получит приращение,
тогда (8) примет вид:
(11)
Разделим
обе части на
,
получим:
,
(12)
где
отношение
— есть среднее угловое ускорение.
т.е.
(13)
Вектор
углового ускорения
сонаправлен с вектором угловой скости
прии противоположен ему при,
см. рис 6.
8. Связь тангенциального и углового ускорения.
При
вращении за время
угловая скорость получит приращение,
тогда (8) примет вид:
(14)
Разделим
обе части на
,
получим:
(15)
или
(16)
Векторное
произведение:
(17)
Вектор тангенциального
ускорениясовпадает по направлению
с векторным произведением.
Векторное произведение всегда связано
справилом правого
винта: вращая головку винта по
направлению вектора,
стоящего на первом месте в (13), к вектору,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора.
9. Мгновенное угловое ускорение.
При
получим мгновенное угловое ускорение:
,
(18)
т.е.
мгновенное угловое ускорение численно
равно первой производной угловой
скорости по времени или – второй
производной углового перемещения по
времени.
Приложение 1.
|
тип |
рисунок, |
формулы |
|
|
Равномерное |
|||
|
Равноускоренное движение |
|||
|
Движение |
При |
||
|
При |
|||
|
Движение |
|||
|
При |
|||
|
Движение |
; ; ; |
||
|
Движение |
|||
|
Движение |
Тангенциальное При движении по Тангенциальное Направление Нормальное Модуль полного . Направление . |
||
Движение
с постоянным ускорением при действии
постоянной силы
Первый
этап — определение типа движения.
Второй
этап — физическая формулировка задачи:
выбор системы отсчета, определение
действующих сил и начальных условий.
Третий
этап — математическая формулировка
задачи: запись уравнений,
Если
md2х/dt2
=F=mа
не
равно 0, то
движение ускоренное
t
= 0, v
= v0;
x=
x0
Четвертый
этап — математическое решение задачи.
a
= d2х/dt2;
или
a
= dv/dt;
Откуда
dv
= adt;
Интегрируя
обе части
∫ dv
=∫ adt;
Взятие
интеграла дает
v
= at
+ C
постоянные
интегрирования определяюся из начальных
условий
Например,
при
t
= 0, v
= v0;
тогда
v
= v0
+ at
или
используя выражение для скорости
dx/dt
= v0
+ at;
разделяя
переменные
dx
=(v0
+ at)dt;
перемножая
почленно
dx
= atdt
+ v0dt;
Применяя
операцию почленного интегрирования(свойство
интеграла суммы)
∫dx
= ∫ atdt
+ ∫
v0dt
Получаем
интеграл
x
= at2/2
+ x0
+ v0t.
Постоянные
интегрирования определяются из начальных
условий для координаты частицы и скорости
Следует
особо!!!!!! Отметить, что задаются
одновременно координата и скорость
частицы
Это
позволяет делать только классическая
механика
Пятый
этап — проверка полученного решения.
Прием
первый — проверка ответа по размерности.
Прием
второй — проверка ответа по заранее
очевидным результатам.
Редко
используемое и неточное выражение для
средней скорости
vср.
=(t)
t1t2
∫vdt
Движение
материальной точки под действием
постоянной силы –размерная задача
Прежде
всего, к такому типу движения относится
при определенных условиях движение под
действием силы тяжести. Сила тяжести,
как и любая сила, является векторной
величиной. Примем упрощающее предположение,
что
ее модуль постоянен. Но так как эта сила
направлена к центру Земли, то ее
направление в разных точках земной
поверхности различно. Однако при
исследовании движений тел, перемещающихся
на расстояния, которые намного меньше
радиуса Земли (R ~ 6000 км), можно
пренебречь
кривизной земной поверхности и с хорошей
точностью считать, что сила тяжести не
меняет своего направления, оставаясь
перпендикулярной этой поверхности. В
В
этих условиях сила тяжести может
рассматриваться постоянной как по
модулю, так и по направлению. Помимо
силы тяжести, с постоянными силами
приходится часто сталкиваться при
рассмотрении работы различных технических
устройств, когда их различные детали
испытывают действие постоянных сил со
стороны других деталей.
Какой
вид имеет траектория камня? От чего
зависит дальность полета? Аристотель
утверждал, например, что на начальном
участке траектория брошенного под углом
к вертикали тела является прямой линией,
и это, вроде бы, подтверждается
непосредственными наблюдениями.
Потребовалось почти два тысячелетия,
чтобы понять, что траектория на самом
деле является криволинейной на всех
участках полета.
Изучение
движения брошенного тела включает в
себя несколько этапов, характерных для
решения большинства задач механики.
Первый
этап — определение типа движения.
Второй
этап — физическая формулировка задачи:
выбор системы отсчета, определение
действующих сил и начальных условий.
любая
точка поверхности движется с ускорением,
обусловленным вращением Земли вокруг
своей оси и вокруг Солнца. Но для многих
практических задач этот эффект
«неинерциальности» является несущественным,
и мы будем полагать, что и в нашей задаче
этим эффектом можно пренебречь и считать
выбранную систему отсчета инерциальной.
В инерциальной системе отсчета справедлив
второй закон Ньютона , где теперь под F
подразумевается постоянная сила тяжести.
Мы изобразили эту силу на рис. 4.2 а для
некоторого произвольного момента
времени после начала движения, поместив
тело известной массы в некоторой
произвольной точке над поверхностью.
Истинное положение тела в различные
моменты времени, то есть траекторию его
движения, мы сможем определить только
после окончательного решения задачи.
рис 4.2
Третий
этап — математическая формулировка
задачи: запись уравнений,
соответствующих физической формулировке.
Уравнение D.3) содержит в качестве
неизвестных векторные величиныr(t)
и v(t). Поэтому оно фактически представляет
Поэтому оно фактически представляет
собой совокупность трех уравнений для
трех проекций вышеупомянутых величин.
Для
проекций радиуса-вектора тела введем
обозначения: rх= х,rу= у, rz = z.
Взяв проекции на оси координат от левой
и правой частей уравнения движения, мы
получаем три уравнения:
Справа
от каждого из уравнений записаны
начальные условия, являющиеся
неотъемлемыми
элементами физической и математической
формулировки задачи. Знак «минус» перед
mgв последнем уравнении
отражает тот факт, что сила тяжести
направлена в отрицательном направлении
осиOz.
Четвертый
этап — математическое решение задачи.Составляющая скоростиvzимеет вид:
Константу
определяем из условия
Интегрируем
еще раз:
Новую
константу определяем из условия z(0)
= 0.
окончательно
решение:
Найденные
выражения определяют зависимость от
времени всех трех проекций радиуса-вектора
тела, движущегося под действием силы
тяжести.
Тем
самым задача о нахождении траектории
движения решена.
достаточно
выразить tчерез х в первом
из равенств и подставить результат в
выражение дляz(t).
Это даетуравнение траекториив плоскостиzOx:
Из
геометрии известно, что это соотношение
представляет собой уравнение
параболической
кривой, и следовательно, ни на одном
из участков полета тела его траектория
не является прямой линией.
дальность
полетатела. При падении на поверхностьz= 0, и из этого условия
находим
Пятый
этап — проверка полученного решения.
Прием
первый — проверка ответа по размерности.
Прием
второй — проверка ответа по заранее
очевидным результатам.
Движение
ракеты
Первый
этап — определение типа движения.
Второй
этап — физическая формулировка задачи:
выбор системы отсчета, определение
действующих сил и начальных условий.
Скорость
выброса газов относительно корпуса
ракеты-известна(конструкция сопла, тип
топлива, параметры горения)-это
относительная скорость.
Задача-найти
скорость ракеты, массу и т.д.
Третий
этап — математическая формулировка
задачи: запись уравнений,
Четвертый
этап — математическое решение задачи.
Формула
Циолковского
Пятый
этап — проверка полученного решения.
Прием
первый — проверка ответа по размерности.
Прием
второй — проверка ответа по заранее
очевидным результатам.
При
переменной во времени скорости истечения
Для
описания движения ракеты в поле Земли
следует добавить силу
Уравнение
Мещерского
Силы
Сила
– степень взаимодействия между объектами
Разложение
сил
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Система СИ
- Путь и перемещение
- Средняя скорость
- Равноускоренное прямолинейное движение
- Свободное падение по вертикали
- Горизонтальный бросок
- Бросок под углом к горизонту (с земли на землю)
- Сложение скоростей
- Равномерное движение по окружности
Система СИ
К оглавлению. ..
..
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку.
 Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее.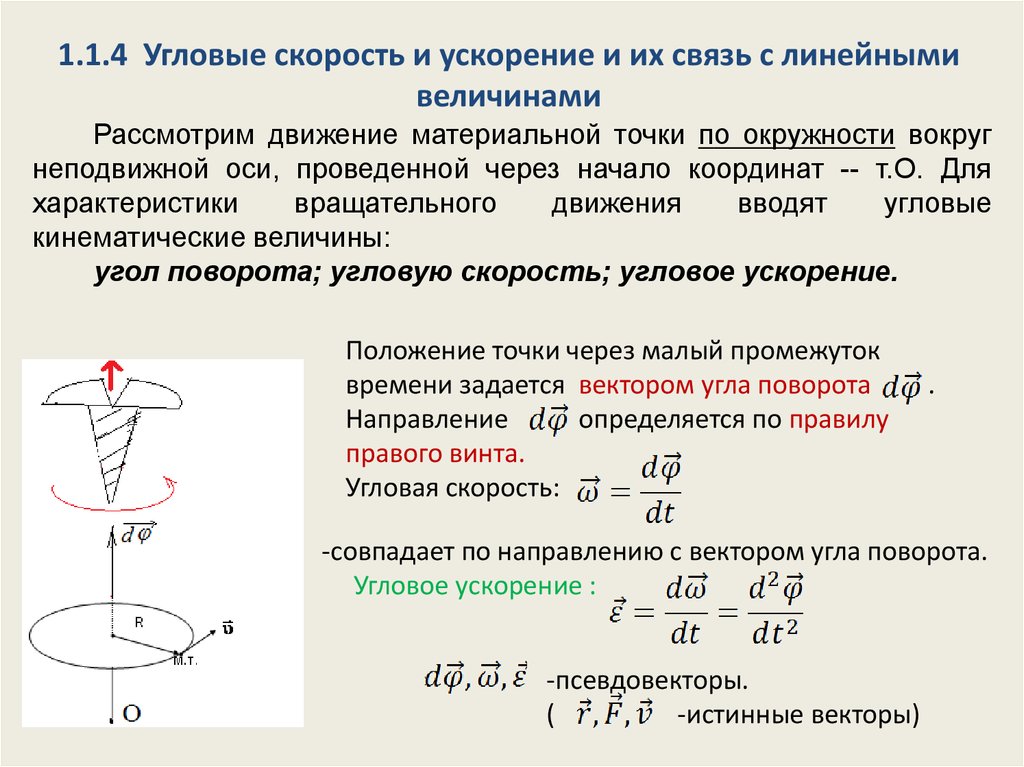 Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории.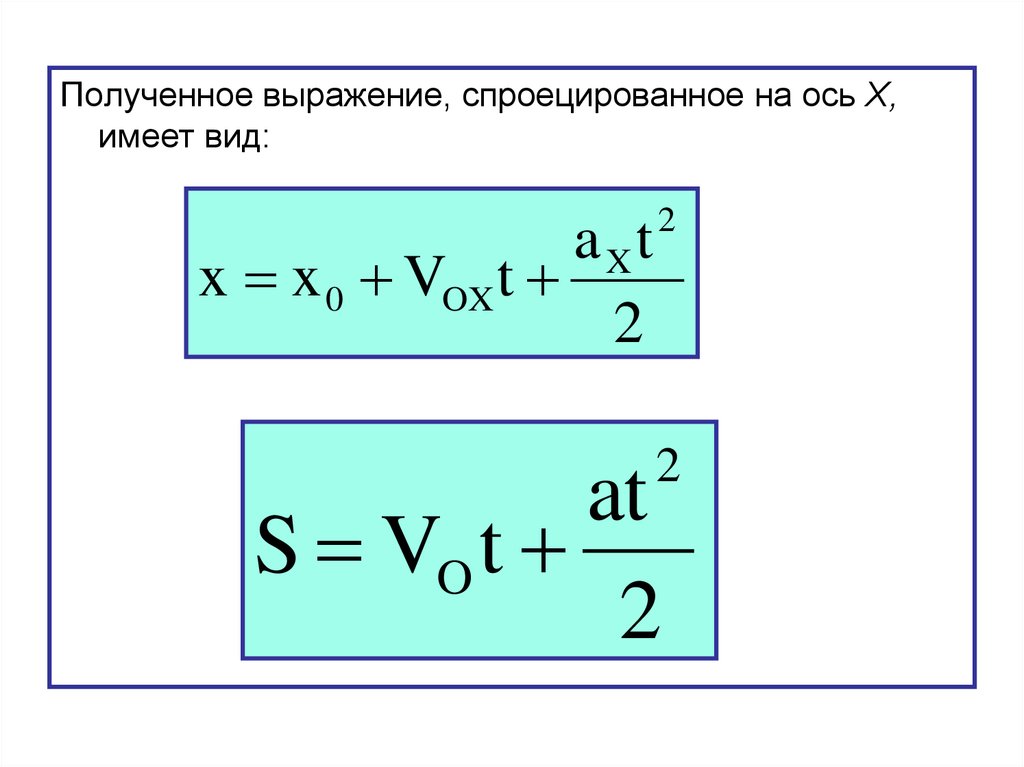 Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.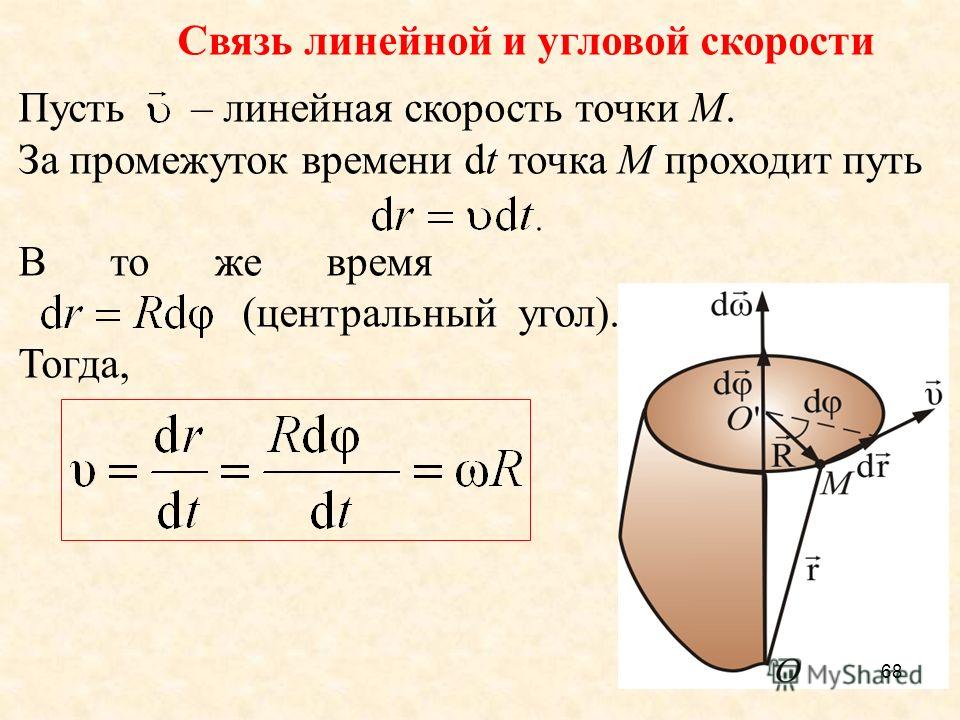 е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета.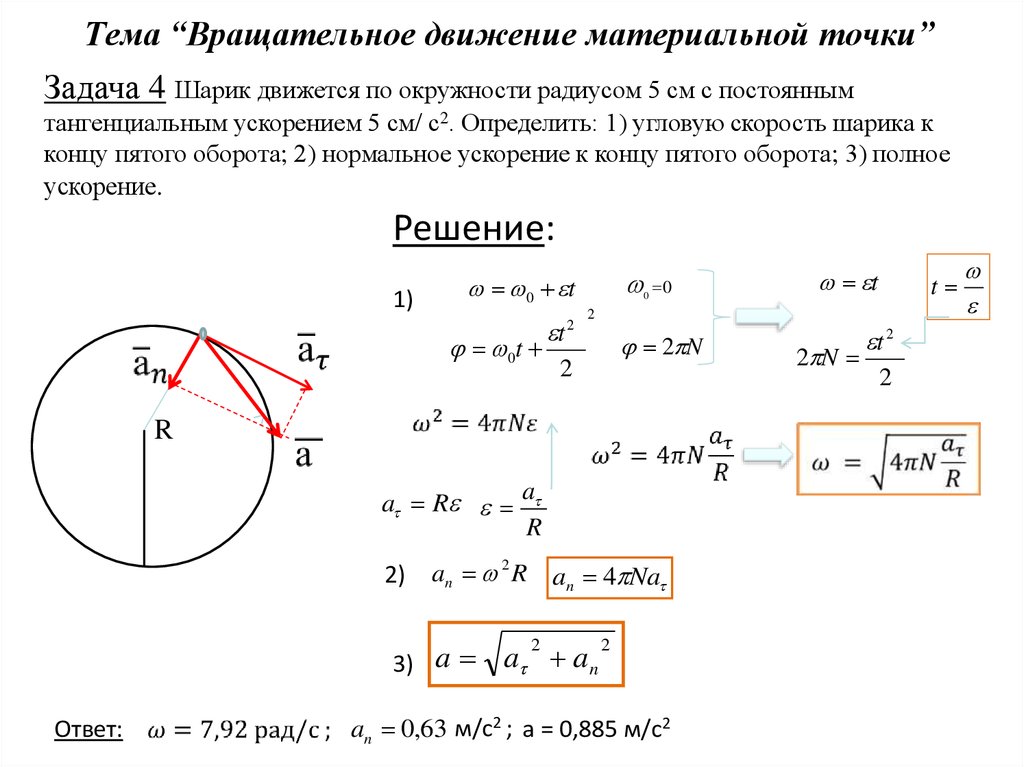 Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
Как видно из вышеприведенных формул, период и частота величины взаимообратные:
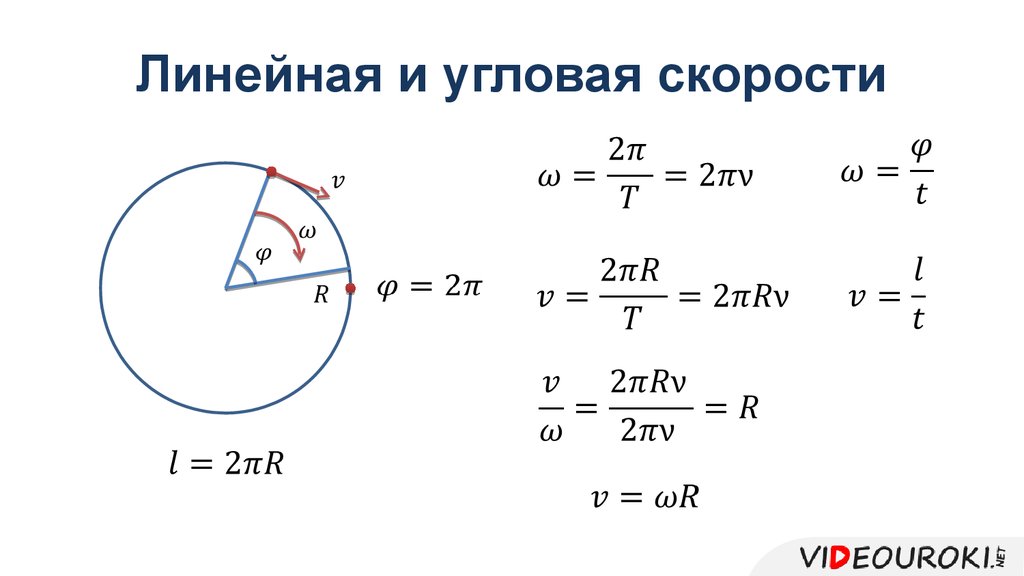
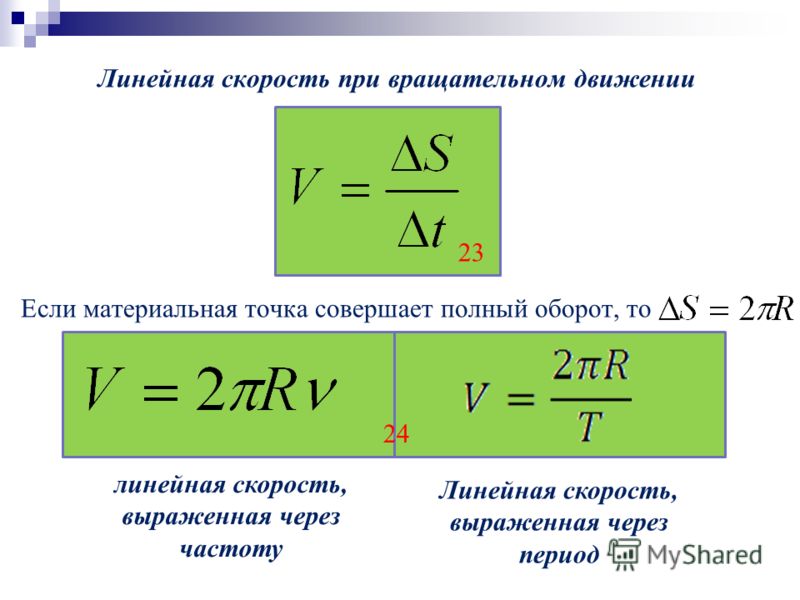
При равномерном вращении скорость тела будет определяется следующим образом:
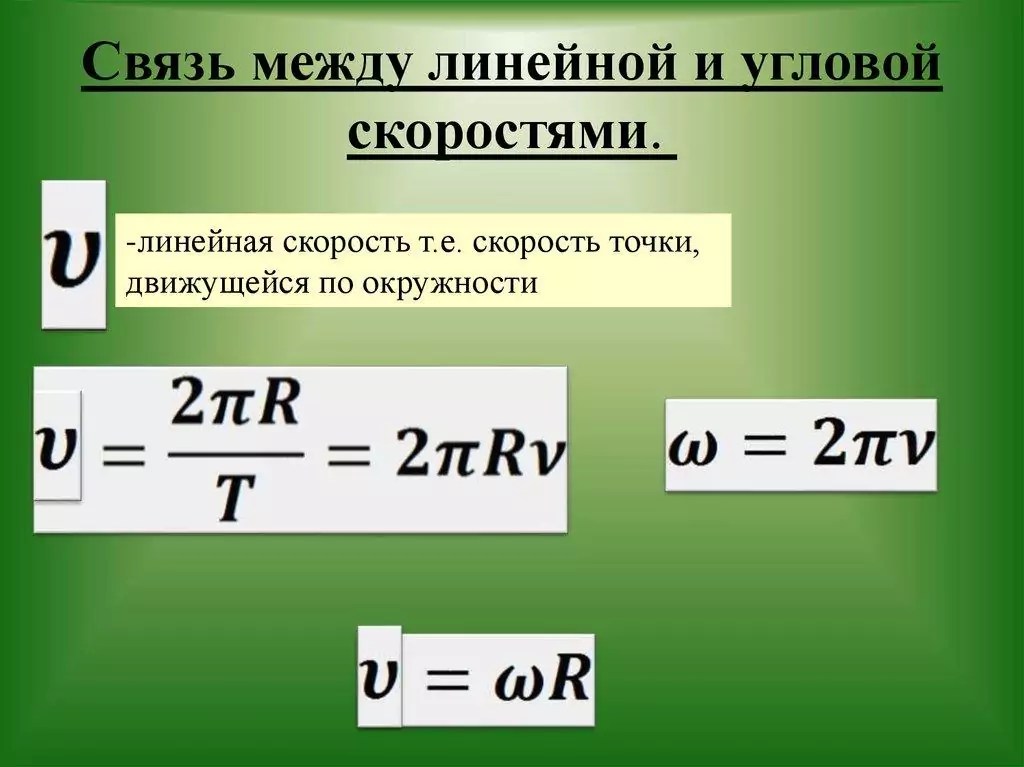
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
3.2 Мгновенная скорость и скорость — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Объясните разницу между средней скоростью и мгновенной скоростью.
- Опишите разницу между скоростью и скоростью.
- Рассчитайте мгновенную скорость по математическому уравнению для скорости.
- Рассчитать скорость по мгновенной скорости.

Теперь мы увидели, как рассчитать среднюю скорость между двумя положениями. Однако, поскольку объекты в реальном мире непрерывно движутся в пространстве и времени, мы хотели бы найти скорость объекта в любой точке. Мы можем найти скорость объекта в любом месте его пути, используя некоторые фундаментальные принципы исчисления. Этот раздел дает нам лучшее представление о физике движения и будет полезен в следующих главах.
Мгновенная скорость
Величина, которая говорит нам, насколько быстро объект движется в любом месте на своем пути, — это мгновенная скорость, обычно называемая просто скоростью . Это средняя скорость между двумя точками на пути в пределе, когда время (и, следовательно, смещение) между двумя событиями приближается к нулю. Чтобы проиллюстрировать эту идею математически, нам нужно выразить позицию x как непрерывную функцию от t , обозначенную как x ( t ). Выражение для средней скорости между двумя точками с использованием этих обозначений имеет вид v–=x(t2)−x(t1)t2−t1v–=x(t2)−x(t1)t2−t1. Чтобы найти мгновенную скорость в любом положении, пусть t1=tt1=t и t2=t+Δtt2=t+Δt. Подставив эти выражения в уравнение для средней скорости и приняв предел в виде Δt→0Δt→0, находим выражение для мгновенной скорости:
Выражение для средней скорости между двумя точками с использованием этих обозначений имеет вид v–=x(t2)−x(t1)t2−t1v–=x(t2)−x(t1)t2−t1. Чтобы найти мгновенную скорость в любом положении, пусть t1=tt1=t и t2=t+Δtt2=t+Δt. Подставив эти выражения в уравнение для средней скорости и приняв предел в виде Δt→0Δt→0, находим выражение для мгновенной скорости:
v(t)=limΔt→0x(t+Δt)−x(t)Δt=dx(t)dt.v(t)=limΔt→0x(t+Δt)−x(t)Δt=dx(t )дт.
Мгновенная скорость
Мгновенная скорость объекта является пределом средней скорости, когда прошедшее время приближается к нулю, или производной от x по отношению к t :
v(t)=ddtx(t).v( т)=ддтх(т).
3,4
Как и средняя скорость, мгновенная скорость представляет собой вектор с размерностью длины во времени. Мгновенная скорость в конкретный момент времени t0t0 представляет собой скорость изменения функции положения, которая представляет собой наклон функции положения x(t)x(t) в момент времени t0t0. На рис. 3.6 показано, как средняя скорость v–=ΔxΔtv–=ΔxΔt между двумя моментами времени приближается к мгновенной скорости в момент времени t0.t0. Мгновенная скорость показана в момент времени t0t0, который оказывается максимальным для функции положения. Наклон графика положения в этой точке равен нулю, и, следовательно, мгновенная скорость равна нулю. В другие моменты времени, t1, t2, t1, t2 и т. д., мгновенная скорость не равна нулю, потому что наклон графика положения будет положительным или отрицательным. Если бы функция положения имела минимум, наклон графика положения также был бы равен нулю, что также давало бы нулевую мгновенную скорость. Таким образом, нули функции скорости дают минимум и максимум функции положения.
На рис. 3.6 показано, как средняя скорость v–=ΔxΔtv–=ΔxΔt между двумя моментами времени приближается к мгновенной скорости в момент времени t0.t0. Мгновенная скорость показана в момент времени t0t0, который оказывается максимальным для функции положения. Наклон графика положения в этой точке равен нулю, и, следовательно, мгновенная скорость равна нулю. В другие моменты времени, t1, t2, t1, t2 и т. д., мгновенная скорость не равна нулю, потому что наклон графика положения будет положительным или отрицательным. Если бы функция положения имела минимум, наклон графика положения также был бы равен нулю, что также давало бы нулевую мгновенную скорость. Таким образом, нули функции скорости дают минимум и максимум функции положения.
Рисунок
3,6
На графике зависимости положения от времени мгновенная скорость представляет собой наклон касательной в данной точке. Средние скорости v–=∆x∆t=xf–xitf–tiv–=∆x∆t=xf–xitf–ti между моментами времени ∆t=t6–t1, ∆t=t5–t2 и ∆t=t4–t3∆t=t6–t1,∆t=t5– показаны t2 и Δt=t4−t3. При Δt→0Δt→0 средняя скорость приближается к мгновенной скорости при t=t0t=t0.
При Δt→0Δt→0 средняя скорость приближается к мгновенной скорости при t=t0t=t0.
Пример
3.2
Определение скорости по графику зависимости положения от времени
Имея график зависимости положения от времени на рис. 3.7, найдите график зависимости скорости от времени.
Рисунок
3,7
Объект начинает движение в положительном направлении, останавливается на короткое время, а затем меняет направление, возвращаясь к исходной точке. Обратите внимание, что объект мгновенно останавливается, что потребовало бы бесконечной силы. Таким образом, график представляет собой приближение движения в реальном мире. (Концепция силы обсуждается в Ньютоновских законах движения.)
Стратегия
График содержит три прямые линии на трех временных интервалах. Мы находим скорость в течение каждого временного интервала, взяв наклон линии с помощью сетки.
Решение
Интервал времени от 0 до 0,5 с: v–=ΔxΔt=0,5 м–0,0 м 0,5 с–0,0 с=1,0 м/сv–=ΔxΔt=0,5 м–0,0 м 0,5 с–0,0 с=1,0 м/с
Время интервал от 0,5 до 1,0 с: v–=ΔxΔt=0,5 м–0,5 м1,0 с–0,5 с=0,0 м/сv–=ΔxΔt=0,5 м–0,5 м1,0 с–0,5 с=0,0 м/с
Интервал времени от 1,0 до 2,0 с: v–=ΔxΔt=0,0 м–0,5 м2,0 с–1,0 с=–0,5 м/сv–=ΔxΔt=0,0 м–0,5 м2,0 с–1,0 с=–0,5 м/с
график зависимости этих значений скорости от времени показан на рис. 3.8.
3.8.
Рисунок
3,8
Скорость положительна для первой части пути, равна нулю, когда объект остановлен, и отрицательна, когда объект меняет направление.
Значение
В течение интервала времени от 0 с до 0,5 с положение объекта удаляется от начала координат, а кривая зависимости положения от времени имеет положительный наклон. В любой точке кривой в течение этого временного интервала мы можем найти мгновенную скорость, взяв ее наклон, равный +1 м/с, как показано на рис. 3.8. В последующем интервале времени, между 0,5 с и 1,0 с, положение не меняется, и мы видим, что наклон равен нулю. От 1,0 до 2,0 с объект движется обратно к началу координат, а наклон составляет -0,5 м/с. Объект изменил направление и имеет отрицательную скорость.
Скорость
В повседневном языке большинство людей используют термины скорость и скорость взаимозаменяемо. Однако в физике они не имеют одинакового значения и являются отдельными понятиями. Одно из основных отличий состоит в том, что скорость не имеет направления; то есть скорость является скаляром.
Однако в физике они не имеют одинакового значения и являются отдельными понятиями. Одно из основных отличий состоит в том, что скорость не имеет направления; то есть скорость является скаляром.
Мы можем рассчитать среднюю скорость, найдя общее пройденное расстояние, деленное на прошедшее время:
Средняя скорость=с –=общее расстояние, прошедшее время. Средняя скорость=с –=общее расстояние, прошедшее время.
3,5
Средняя скорость не обязательно совпадает с величиной средней скорости, которая находится путем деления величины полного смещения на прошедшее время. Например, если поездка начинается и заканчивается в одном и том же месте, общее перемещение равно нулю, и, следовательно, средняя скорость равна нулю. Однако средняя скорость не равна нулю, поскольку общее пройденное расстояние больше нуля. Если мы проедем 300 км и должны быть в пункте назначения в определенное время, то нас будет интересовать наша средняя скорость.
Однако мы можем рассчитать мгновенную скорость по величине мгновенной скорости:
Мгновенная скорость=|v(t)|. Мгновенная скорость=|v(t)|.
3,6
Если частица движется вдоль оси x со скоростью +7,0 м/с, а другая частица движется по той же оси со скоростью -7,0 м/с, то они имеют разные скорости, но обе имеют одинаковую скорость 7,0 м/с. с. Некоторые типичные скорости показаны в следующей таблице.
| Скорость | м/с | миль/ч |
|---|---|---|
| Континентальный дрейф | 10-710-7 | 2×10-72×10-7 |
| Быстрая ходьба | 1,7 | 3,9 |
| Велосипедист | 4,4 | 10 |
| Спринтер | 12,2 | 27 |
| Ограничение скорости в сельской местности | 24,6 | 56 |
| Официальный рекорд наземной скорости |
341. 1 1
|
763 |
| Скорость звука на уровне моря | 343 | 768 |
| Космический корабль при входе в атмосферу | 7800 | 17 500 |
| Убегающая скорость Земли* | 11 200 | 25 000 |
| Орбитальная скорость Земли вокруг Солнца | 29 783 | 66 623 |
| Скорость света в вакууме | 299,792458 | 670 616 629 |
Стол
3. 1
1
Скорости различных объектов
* Убегающая скорость — это скорость, с которой объект должен быть запущен, чтобы он преодолел гравитацию Земли и не был притянут обратно к Земле.
Расчет мгновенной скорости
При расчете мгновенной скорости необходимо указать явный вид функции положения x(t)x(t). Если каждый член в уравнении x(t)x(t) имеет форму AtnAtn, где AA — константа, а nn — целое число, это можно дифференцировать с помощью правила степени:
d(Atn)dt=Antn-1.d(Atn)dt=Antn-1.
3,7
Обратите внимание, что если есть дополнительные члены, сложенные вместе, это степенное правило дифференцирования может быть выполнено несколько раз, и решение будет суммой этих членов. Следующий пример иллюстрирует использование уравнения 3.7.
Пример
3.3
Мгновенная скорость в сравнении со средней скоростью
Положение частицы определяется выражением x(t)=(3,0 м/с)t+(0,5 м/с3)t3x(t)=(3,0 м/с)t+(0,5 м/с3)t3.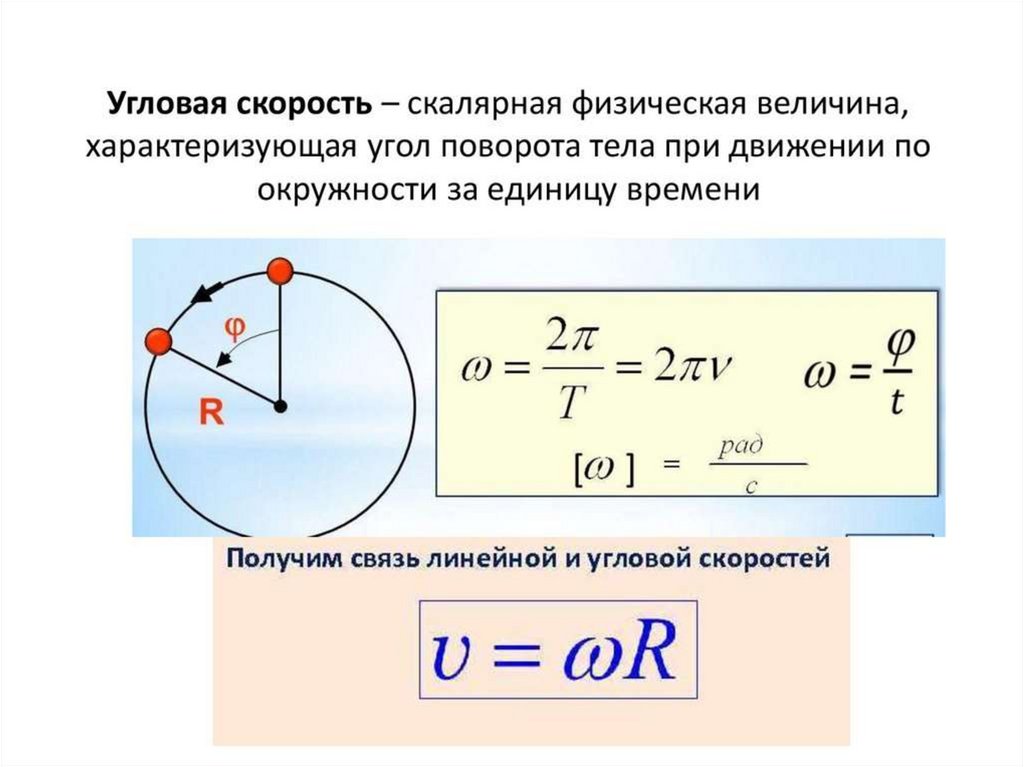
- Используя уравнения 3.4 и 3.7, найдите мгновенную скорость при t=2,0t=2,0 с.
- Рассчитайте среднюю скорость между 1,0 и 3,0 с.
Стратегия
Уравнение 3.4 дает мгновенную скорость частицы как производную функции положения. Глядя на форму данной функции положения, мы видим, что это полином от t . Следовательно, мы можем использовать уравнение 3.7, степенное правило исчисления, чтобы найти решение. Мы используем уравнение 3.6 для расчета средней скорости частицы.
Решение
- v(t)=dx(t)dt=(3,0 м/с)+(1,5 м/с3)t2v(t)=dx(t)dt=(3,0 м/с)+(1,5 м/с3)t2.
Подстановка t = 2,0 с в это уравнение дает v(2,0 с)=(3,0 м/с)+(1,5 м/с3)(2,0 с)2v(2,0 с)=(3,0 м/с)+(1,5 м/с3)(2,0 с)2. - Чтобы определить среднюю скорость частицы между 1,0 и 3,0 с, мы вычисляем значения x (1,0 с) и x (3,0 с):
x(1,0 с)=[(3,0 м/с)(1,0 с)+(0,5 м/с3)(1,0 с)3]=3,5 м x(1,0 с)=[(3,0 м/с)(1,0 с) +(0,5 м/с3)(1,0 с)3]=3,5 м
x(3,0 с)=[(3,0 м/с)(3,0 с)+(0,5 м/с3)(3,0 с)3]=22,5 м x(3,0 с)=[(3,0 м/с)(3,0 с) +(0,5 м/с3)(3,0 с)3]=22,5 м
Тогда средняя скорость
v–=x(3,0 с)−x(1,0 с)t(3,0 с)−t(1,0 с)=(22,5−3,5)m(3,0−1,0)с=9,5 м/с.
 v–=x(3,0 с) )−x(1,0 с)t(3,0 с)−t(1,0 с)=(22,5−3,5)m(3,0−1,0)с=9,5 м/с.
v–=x(3,0 с) )−x(1,0 с)t(3,0 с)−t(1,0 с)=(22,5−3,5)m(3,0−1,0)с=9,5 м/с.
Значение
В пределе, когда временной интервал, используемый для вычисления v-v-, стремится к нулю, значение, полученное для v-v-, сходится к значению v.
Пример
3.4
Мгновенная скорость в сравнении со скоростью
Рассмотрим движение частицы, положение которой x(t)=(3,0 м/с)t–(3 м/с2)t2x(t)=(3,0 м/с)t–(3 м/с2)t2.
- Чему равна мгновенная скорость в точках t = 0,25 с, t = 0,50 с и t = 1,0 с?
- Какова скорость частицы в эти моменты времени?
Стратегия
Мгновенная скорость является производной функции положения, а скорость является величиной мгновенной скорости. Мы используем уравнение 3.4 и уравнение 3.7 для определения мгновенной скорости.
Мы используем уравнение 3.4 и уравнение 3.7 для определения мгновенной скорости.
Решение
- v(t)=dx(t)dt=(3,0 м/с–6,0 м/с2t)v(0,25 с)=1,50 м/с,v(t)=dx(t)dt= (3,0 м/с–6,0 м/с2t)v(0,25 с)=1,50 м/с,
v(0,5 с)=0 м/с,v(1,0 с)=−3,0 м/сv(0,5 с)=0 м /с,v(1,0с)=-3,0м/с - Скорость=|v(t)|=1,50 м/с, 0,0 м/с и 3,0 м/с Скорость=|v(t)|=1,50 м/с, 0,0 м/с и 3,0 м/с
Значение
Скорость частицы дает нам информацию о направлении, указывая на то, что частица движется влево (запад) или вправо (восток). Скорость дает величину скорости. Изобразив положение, скорость и скорость как функции времени, мы можем визуально понять эти понятия. Рисунок 3.9. На (а) график показывает движение частицы в положительном направлении до t = 0,5 с, когда она меняет направление. Изменение направления также можно увидеть на (b) в момент времени 0,5 с, когда скорость равна нулю, а затем становится отрицательной.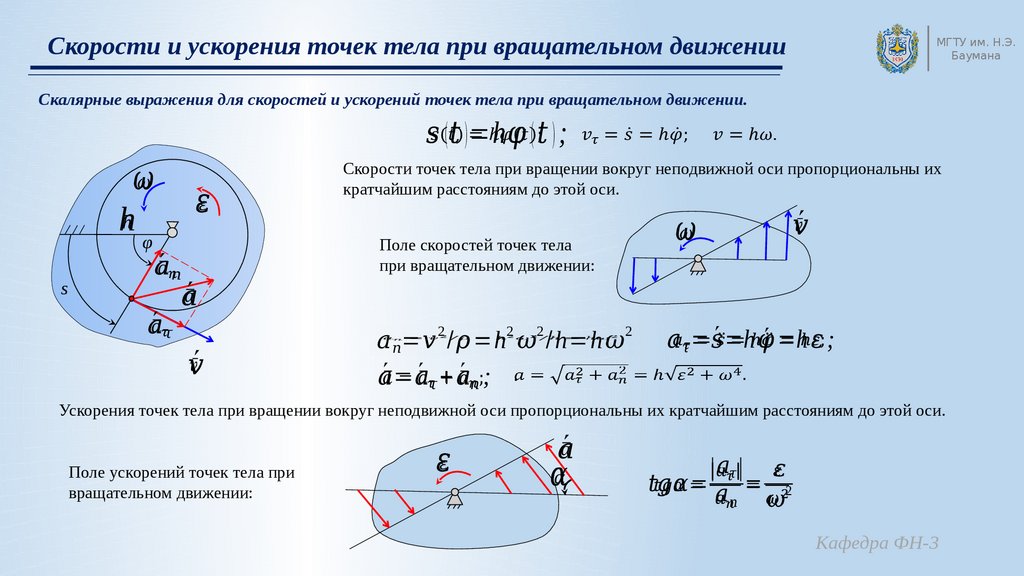 В 1,0 с он возвращается в исходное положение, откуда начал. Скорость частицы в 1,0 с в (b) отрицательна, потому что она движется в отрицательном направлении. Но в (с), однако, его скорость положительна и остается положительной на протяжении всего времени движения. Мы также можем интерпретировать скорость как наклон графика зависимости положения от времени. Склон x ( t ) уменьшается до нуля, становится нулем через 0,5 с и после этого становится все более отрицательным. Такой анализ сравнения графиков положения, скорости и скорости помогает выявить ошибки в расчетах. Графики должны согласовываться друг с другом и помогать интерпретировать расчеты.
В 1,0 с он возвращается в исходное положение, откуда начал. Скорость частицы в 1,0 с в (b) отрицательна, потому что она движется в отрицательном направлении. Но в (с), однако, его скорость положительна и остается положительной на протяжении всего времени движения. Мы также можем интерпретировать скорость как наклон графика зависимости положения от времени. Склон x ( t ) уменьшается до нуля, становится нулем через 0,5 с и после этого становится все более отрицательным. Такой анализ сравнения графиков положения, скорости и скорости помогает выявить ошибки в расчетах. Графики должны согласовываться друг с другом и помогать интерпретировать расчеты.
Рисунок
3,9
(а) Положение: x ( t ) в зависимости от времени. (b) Скорость: v ( t ) в зависимости от времени. Наклон графика положения — это скорость. Грубое сравнение наклонов касательных линий на (а) через 0,25 с, 0,5 с и 1,0 с со значениями скорости в соответствующие моменты времени показывает, что это одни и те же значения. (c) Скорость: |v(t)||v(t)| против времени. Скорость всегда положительное число.
Грубое сравнение наклонов касательных линий на (а) через 0,25 с, 0,5 с и 1,0 с со значениями скорости в соответствующие моменты времени показывает, что это одни и те же значения. (c) Скорость: |v(t)||v(t)| против времени. Скорость всегда положительное число.
Проверьте свое понимание
3.2
Положение объекта как функция времени: x(t)=(–3 м/с2)t2x(t)=(–3 м/с2)t2. а) Какова зависимость скорости тела от времени? б) Всегда ли скорость положительна? в) Каковы скорость и скорость в момент времени t = 1,0 с?
Чем мгновенная скорость отличается от средней скорости?
Скорость — ключевая тема в физике. Многие свойства тела, такие как кинетическая энергия и вязкость, зависят от его скорости. Термин скорость описывает, насколько быстро или медленно движется объект. Скорость можно определить как скорость изменения положения объекта по отношению ко времени и системе отсчета. В таких разнообразных дисциплинах, как кинематика, кинетика, динамика, астрофизика и инженерия, обычно применяется понятие скорости. Чтобы преуспеть в таких дисциплинах, очень важно хорошо знать понятия мгновенной скорости и средней скорости. В этой статье мы подробно рассмотрим, чем мгновенная скорость отличается от средней скорости.
Чтобы преуспеть в таких дисциплинах, очень важно хорошо знать понятия мгновенной скорости и средней скорости. В этой статье мы подробно рассмотрим, чем мгновенная скорость отличается от средней скорости.
Мгновенная скорость
Скорость изменения положения за относительно короткий промежуток времени называется мгновенной скоростью или скоростью объекта в этот момент времени. Мгновенная скорость может быть рассчитана путем умножения мгновенной скорости объекта на направление, в котором он движется в данный момент времени. Скорость изменения смещения описывается как скорость в классической физике. Термин «скорость» относится к векторной величине. Они имеют числовое значение, а также направление. Объект с постоянной скоростью может иметь ту же немедленную скорость, что и его стандартная скорость. Международная система единиц (СИ) мгновенной скорости составляет метры в секунду (м/с).
Рассчитывается как средняя скорость, деленная на минимальный период. Отношение полного смещения к общему времени можно использовать для вычисления средней скорости. Смещение пропорционально интервалу времени. Предел этого отношения между временем и перемещением известен как мгновенная скорость.
Смещение пропорционально интервалу времени. Предел этого отношения между временем и перемещением известен как мгновенная скорость.
Где
- V(t) мгновенная скорость в момент времени t0008
Наклон касательной к функции в этом месте равен мгновенной скорости в любой заданной точке функции x(t). Наклон графика расстояние-время, часто известный как график x-t, также может быть использован для его иллюстрации. Формула мгновенной скорости:
Скорость между двумя положениями в пределе времени, когда время между ними постепенно становится равным 0, называется мгновенной скоростью. Расположение x по отношению к функции t обозначается X (t). Ниже приводится уравнение для средней скорости между двумя точками:
Пусть, t 1 и t 2 и
Δt должно быть равно 0, чтобы определить мгновенную скорость,
Используя Таким образом в качестве предела и подставляя выражения в уравнение
V(t) = dx/dt
Средняя скорость
Средняя скорость рассчитывается путем деления изменения полного смещения на общее время.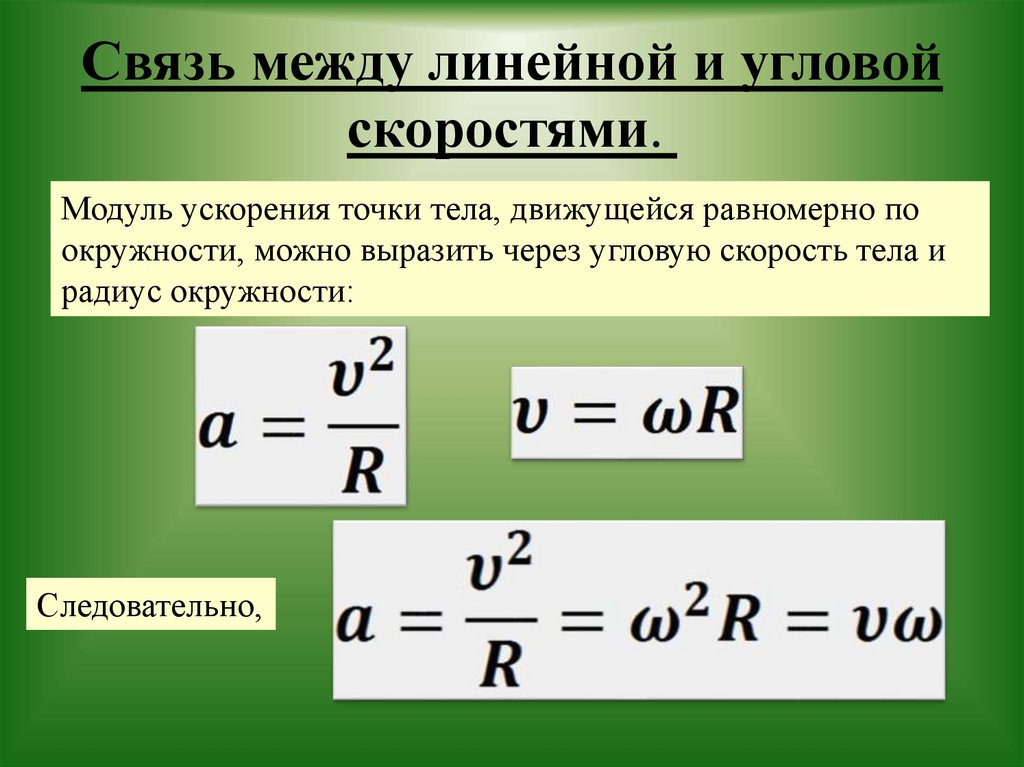 Средняя скорость объекта всегда меньше или равна его средней скорости. Это можно продемонстрировать, заметив, что в то время как расстояние всегда строго возрастает, смещение может менять направление, а также увеличиваться или уменьшаться по величине. Средняя скорость в Международной системе единиц (СИ) составляет метры в секунду (м/с)
Средняя скорость объекта всегда меньше или равна его средней скорости. Это можно продемонстрировать, заметив, что в то время как расстояние всегда строго возрастает, смещение может менять направление, а также увеличиваться или уменьшаться по величине. Средняя скорость в Международной системе единиц (СИ) составляет метры в секунду (м/с)
, где
- x 1 является окончательным смещением
- x 0 — начальное смещение
- T 1 — это время, занятое на последнем положении
- , T 1 — это время, занятое на последнем положении
- 7 T 1 . время пребывания в начальном положении
Средняя скорость определяется как наклон секущей, соединяющей две точки с координатами t, соответствующие границам периода времени.
Средняя скорость равна скорости, усредненной по времени, или ее взвешенному по времени среднему значению, которое может быть определено как интеграл скорости по времени.
, где мы можем узнать,
и
△ T = T 1 — T 0
DINIE Мгновенная скорость
|
Средняя скорость |
||||||||
|
|
|||||||
|
|
1111118
|
1111118
|
1118
|
11118
|
Обратовые вопросы3 |
.
 Образец
Образец
. положение предоставленной частицы x(t) = 2,0t + 0,7 3 м, рассчитайте мгновенную скорость при t = 3,0 с.
Решение:
Дано
x(t) = 2,0t + 0,7 3 M
T = 3 Sec
V = 2T + 3 × 0,7 × T 2
V = 2T + 2,1T 2
AT = 3SEC
V = 2. + 3 × 0,7 × 3 2
v = 6 + 2,1 × 9
v = 6 + 18 – 9
v = 24,9 м/с
t) = 4 с, используя функцию x = 3t 2 – 5t + 2, чтобы получить положение движущегося автобуса.
Решение:
. – 5
V = 6 × 4 – 5
V = 19 м/с
Вопрос 3: За какое минимальное время хищник поймает добычу на расстоянии 200 м, если его средняя скорость равна 90 км/час?
Решение:
Дано,
V = 90 × 5/18 м/с
V = 25 м/с
A = 625/400
A = 1,56 м/с
T 2
- 14
T 2 4
T 2
- 14
T 2
- 9
= 400/1,56
T 2 = 256,4
T 2 = 16 сек
Вопрос 4: S (T) = 9t + 12T 2 — уравнение для автомобиля в автомобиль в A в A -A + 12T 2 .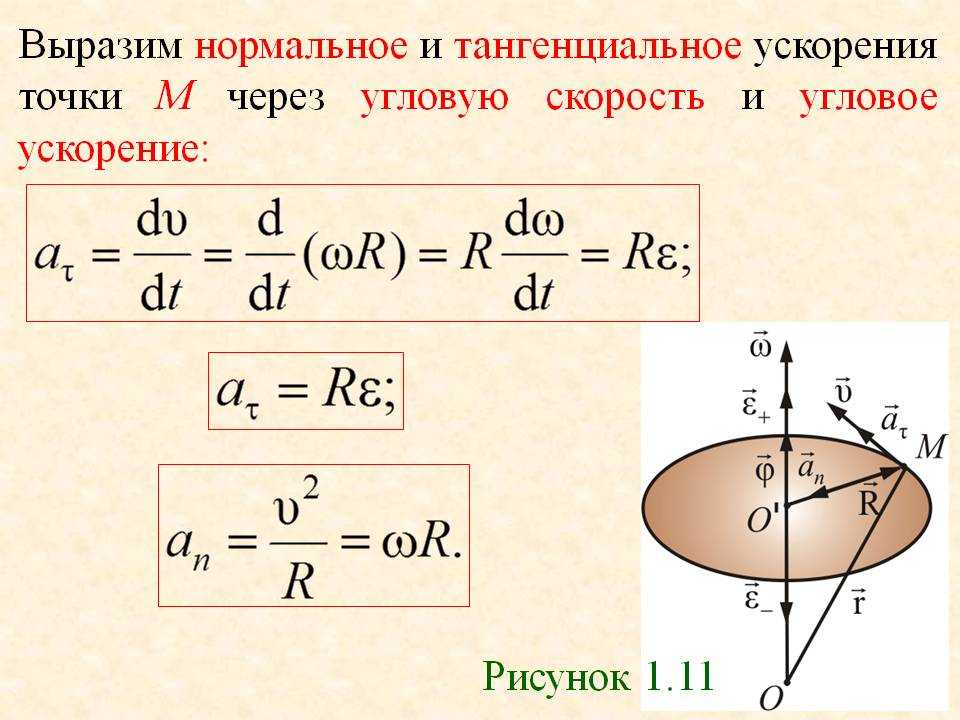 прямой путь в течение 15 секунд до аварии. Вычислите мгновенную скорость в точке 9.й-секундный интервал.
прямой путь в течение 15 секунд до аварии. Вычислите мгновенную скорость в точке 9.й-секундный интервал.
Решение:
,
S (T) = 9T + 12T 2
V = 9 + 24T
Следовательно V INST AT =
5
V . + 24(9)
V = 225 м/с
Вопрос 5: С функцией x = 7t 2 + 3t + 3a данный снаряд движется по прямой за время (t) = 2с. Вычислите мгновенную скорость движущегося тела.
Решение:
. V(2) = 14(2) + 3
V(2) = 31 м/с
Вопрос 6. За 4 минуты водитель автобуса проезжает 15 километров по дороге. Затем он сделал шаг назад и проехал 9 километров по дороге за 2 минуты. Какова его типичная скорость?
Решение:
Средняя скорость (V AVG ) =
Средняя скорость (V AVG ) = 6/6
Средняя скорость (V AVG ) = 1KM/M
444444444444444444444444444444444444444444444444444444444544445444544445449e
-
4444444444444444449549.


 Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.

 v–=x(3,0 с) )−x(1,0 с)t(3,0 с)−t(1,0 с)=(22,5−3,5)m(3,0−1,0)с=9,5 м/с.
v–=x(3,0 с) )−x(1,0 с)t(3,0 с)−t(1,0 с)=(22,5−3,5)m(3,0−1,0)с=9,5 м/с.