Содержание
Таблица знаков в геометрии и их значения: пересечение, подобие
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Знаки и символы в геометрии
Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.
ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ostr-ugol.png" />»>ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/pryamoy-ugol.png" />»>ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" class="stbSkipLazy aligncenter size-full" width="40" height="40" data-full="https://microexcel.ru/wp-content/uploads/2020/01/tupoy-ugol.png" />»>ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" class="stbSkipLazy aligncenter size-full" width="80" height="240" data-full="https://microexcel.ru/wp-content/uploads/2020/01/razvernuty-ugol-1.png" />»>ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-exc.png" />»>ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/line-segment-exc.png" />»>ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" class="stbSkipLazy aligncenter size-full" width="35" height="35" data-full="https://microexcel.ru/wp-content/uploads/2020/01/ray-exc.png" />»>ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" class="stbSkipLazy aligncenter size-full" width="30" height="30" data-full="https://microexcel.ru/wp-content/uploads/2020/01/arc-exc.png" />»>141592654…</nobr>» data-order=»<nobr>π = 3.141592654…</nobr>»>π = 3.141592654…| Знак | Название | Значение/описание | Пример |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | ∠ABC = 30° |
| острый угол | угол от 0 до 90 градусов | ∠AOB = 60° | |
| прямой угол | угол, равный 90 граусам | ∠AOB = 90° | |
| тупой угол | угол от 90 до 180 градусов | ∠AOB = 120° | |
| развернутый угол | угол, равный 180 градусам | ∠AOB = 180° | |
| ° (или deg) |
градус | единица измерения угла, равна 1/360 окружности | 45° |
| ′ | минута | единица измерения угла, 1° = 60′ | α = 70°59′ |
| ″ | секунда | единица измерения угла, 1′ = 60″ | α = 70°59′59″ |
| линия | бесконечная прямая без начала и конца | ||
| отрезок | участок на прямой между точками A и B | ||
| луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | ||
| дуга | дуга, образованная между точками A и B | ||
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| || | параллельность | непересекающиеся прямые (линии) | AB || CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность |
элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, π = C/d | |
| рад (rad) или c |
радиан | единица измерения угла | 360° = 2π c |
microexcel. ru
ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Как понять Геометрию? Основы с нуля
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.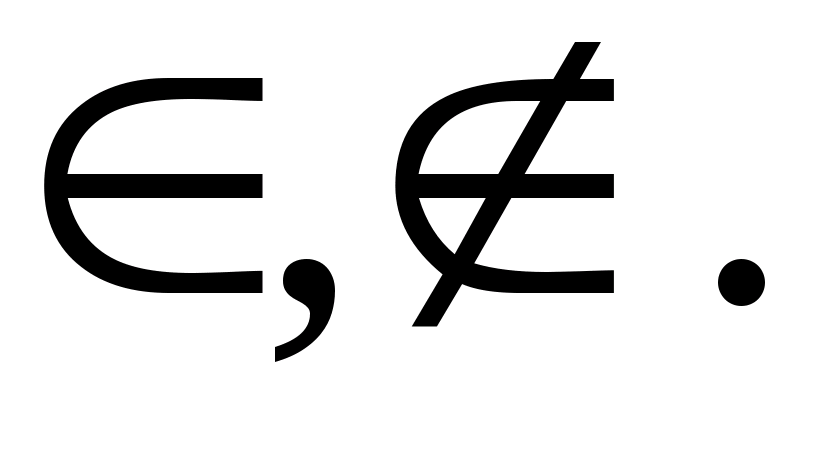
Математика занимается объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец.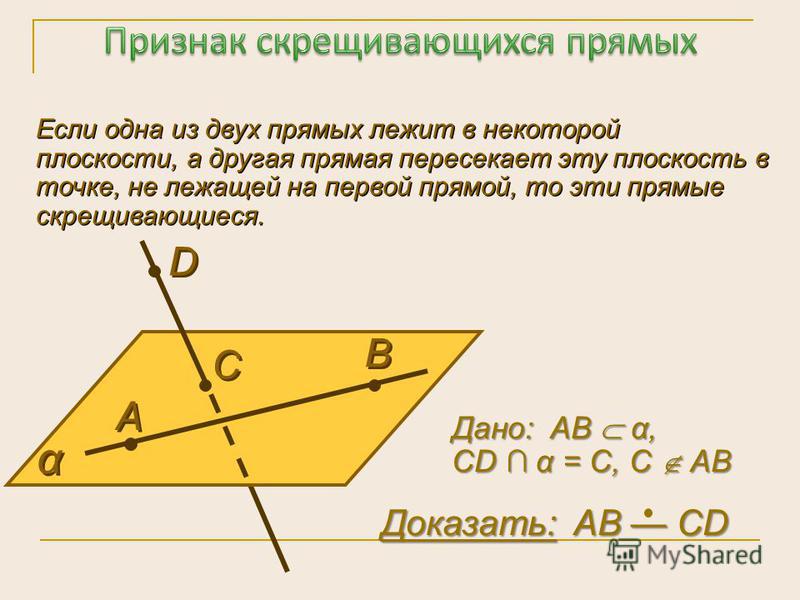 На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b, c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
-
Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).

-
Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).
Важно знать
Через любые две точки можно провести прямую и притом только одну.
Если рассмотреть две прямые, то возможны два варианта их расположения:
-
Прямые пересекаются, то есть имеют одну общую точку.
Для записи пересекающихся прямых используют специальный знак — ∩, то есть a∩b (читают: прямая a пересекает прямую b). Чтобы обозначить точку пересечения прямых, пишут a∩b = O (читается: прямая a пересекается с прямой b в точке O).

- Прямые не пересекаются, то есть не имеют общих точек.
Для записи не пересекающихся прямых используют специальный знак — , то есть m n (читают: прямая m не пересекает прямую n). В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
-
Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
-
Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы.![]() По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
-
Если градусная мера угла меньше 90° — угол острый.
-
Если градусная мера угла равна 90° — угол прямой.
-
Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
-
Если градусная мера угла равна 180° — угол развернутый.

Общая точка, из которой исходят лучи, называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
|
Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны. |
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
-
площадь фигуры
-
периметр фигуры
-
площадь прямоугольника
-
периметр прямоугольника
-
площадь квадрата
-
периметр квадрата
-
параллелограмм
-
прямоугольный параллелепипед.

Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Обозначение
. Есть ли какой-либо символ для пересечений?
спросил
Изменено
7 лет, 5 месяцев назад
Просмотрено
680 раз
$\begingroup$
Для двух многоугольников $A$ и $B$ их пересечение представлено обозначением $A \cap B$, которое возвращает геометрию (точнее, набор точек пересечения), полученную в результате операции пересечения.
Есть ли какой-нибудь символ пересечения (логическая функция, возвращающая 0 (ложь) или 1 (истина), если $A$ пересекает $B$)?
В противном случае, что было бы хорошей записью для этого?
Спасибо!
- обозначение
$\endgroup$
$\begingroup$
Я не знаю никаких специальных обозначений для этого.
А как насчет
$$A\cap B\ne\emptyset$$
Это утверждение верно, если $A$ и $B$ пересекаются, иначе неверно.
Возвращает true для любых перекрытий, включая ребра и вершины. Если вы хотите их исключить, используйте обозначение внутренней части полигонов, $\operatorname{int}(A)\cap\operatorname{int}(B)\ne\emptyset$.
$\endgroup$
1
$\begingroup$
Характеристическая функция множества $S$ равна $$\chi_S(x) = \begin{cases}1,& x\in S\\0,& x\notin S\end{cases}.$$
Итак, что вы ищете, это $$\sup_{x\in\mathcal U}\chi_{A\cap B}(x),$$
где $\mathcal U$ — наш универсальный набор (т. е. $A,B\subset\mathcal U$).
$\endgroup$
2
$\begingroup$
Это немного неудобно, но, возможно, вы могли бы использовать $\not\perp$, потому что, согласно этой странице Википедии:
обозначение $a \perp b$ иногда используется для обозначения того, что $a$ и $b$ взаимно просты
использование, которое может быть распространено на общую решетку (если только символ $\bot$ уже не использовался для обозначения нижнего элемента, что в данном случае не будет проблемой).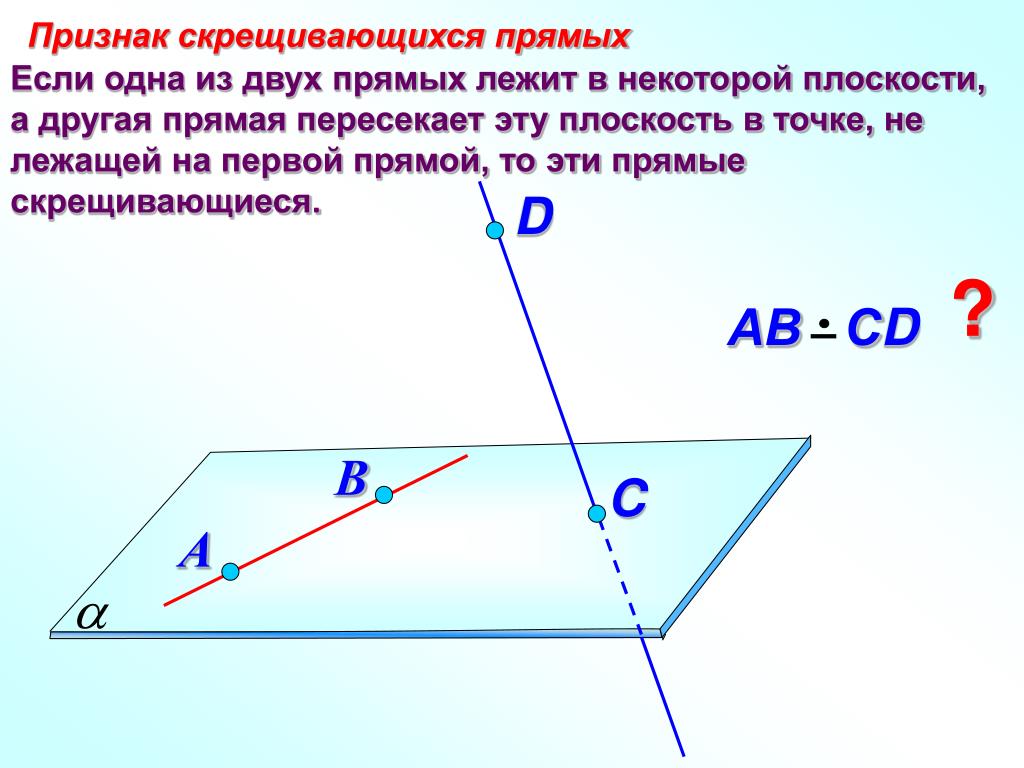
Обозначение (для случая взаимно простых целых чисел), по-видимому, было изобретено Рональдом Л. Грэмом, Дональдом Э. Кнутом и Ореном Паташником, Concrete Mathematics (2-е издание, 1989 г.), раздел 4.5.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
геометрия — Это правильный вопрос?
Задавать вопрос
спросил
Изменено
6 лет, 3 месяца назад
Просмотрено
144 раза
$\begingroup$
Q.
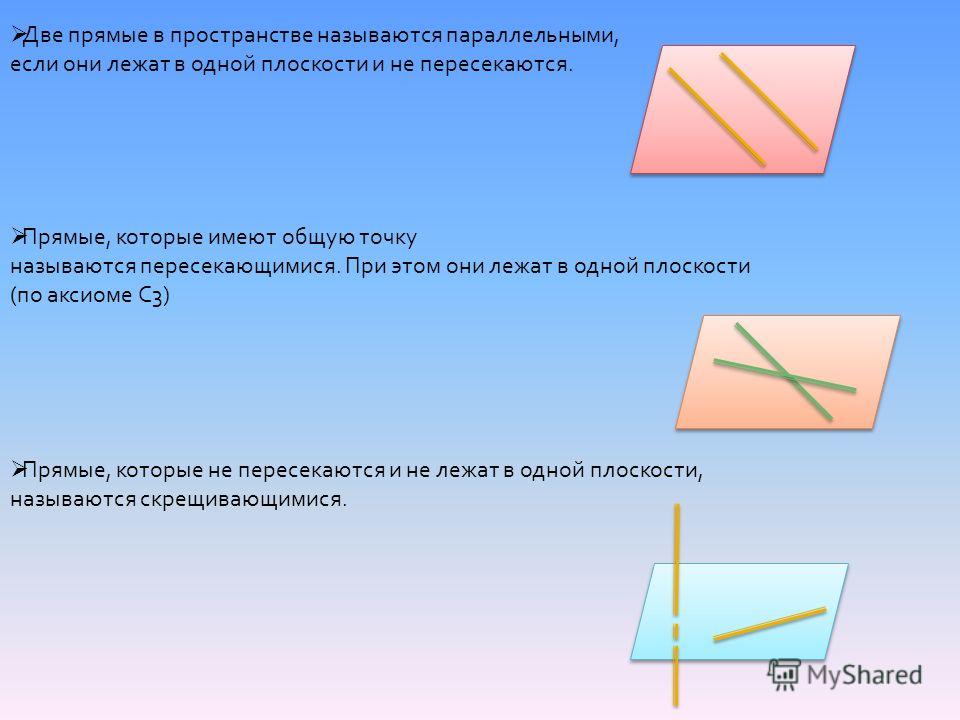
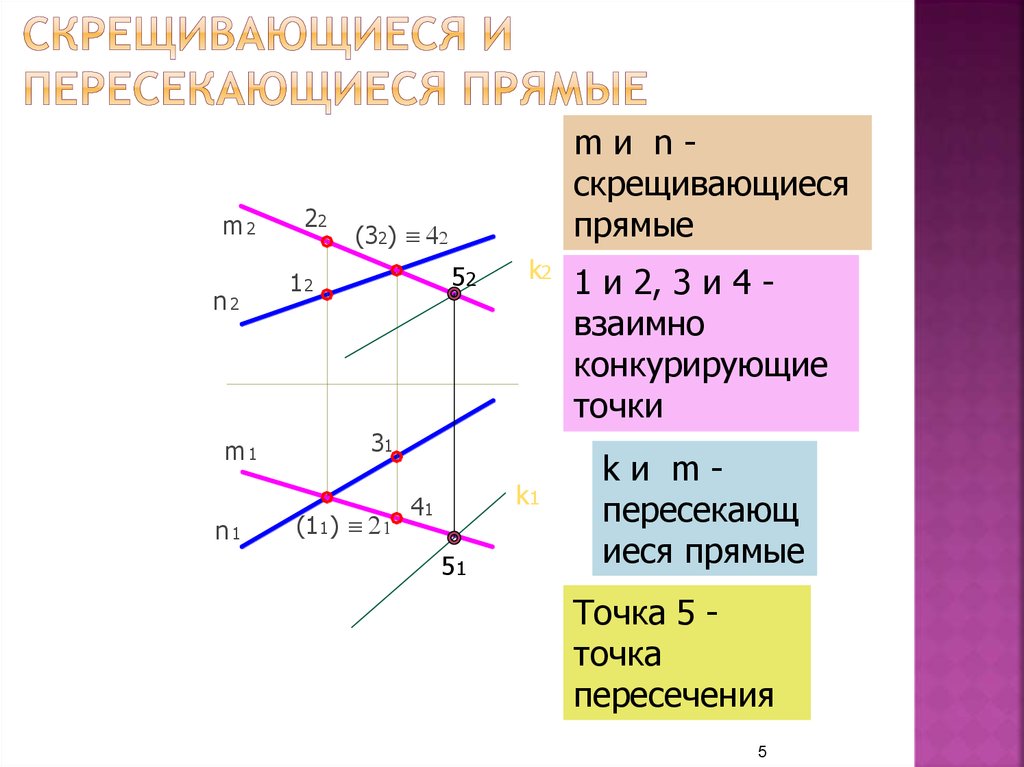
Найдите кратчайшее расстояние между двумя непересекающимися прямыми , проходящими через точки, векторы положения которых a и b параллельны векторам c и d соответственно.
Меня смущает: две непересекающиеся линии должны быть всегда параллельны . Между ними должно быть постоянное расстояние . Какой смысл спрашивать кратчайшее расстояние между двумя прямыми, если они параллельны?
Википедия говорит:
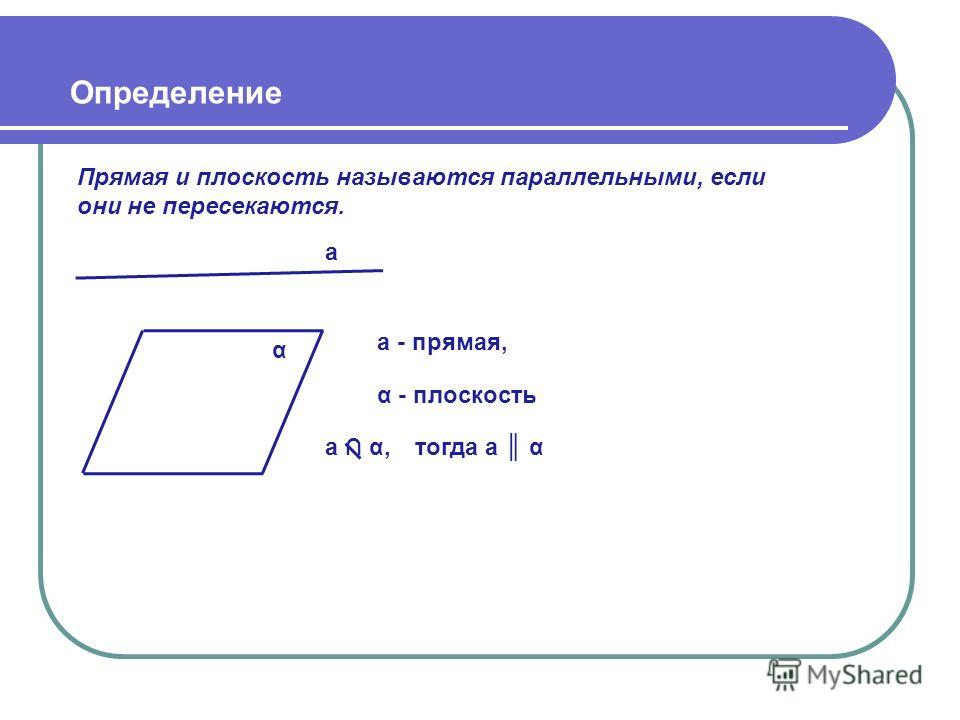
В геометрии параллельные прямые — это прямые на плоскости , которые не пересекаются с ; то есть две линии на плоскости , которые не пересекаются и не касаются друг друга ни в какой точке, называются параллельными. В более широком смысле линия и плоскость или две плоскости в трехмерном евклидовом пространстве, которые не имеют общей точки , называются параллельными.

 Найдите кратчайшее расстояние между двумя непересекающимися прямыми , проходящими через точки, векторы положения которых a и b параллельны векторам c и d соответственно.
Найдите кратчайшее расстояние между двумя непересекающимися прямыми , проходящими через точки, векторы положения которых a и b параллельны векторам c и d соответственно.