УГЛОВАЯ ЧАСТОТА — это что такое УГЛОВАЯ ЧАСТОТА

Значение слова «УГЛОВАЯ ЧАСТОТА» найдено в 24 источниках

найдено в «Большой Советской энциклопедии»

        круговая частота, число полных колебаний, совершающихся при периодическом колебательном процессе за 2π единиц времени. У. ч. ω связана с периодом колебаний Т и частотой колебаний f зависимостью ω = 2πf = 2π/Т.

найдено в «Современной энциклопедии»

УГЛОВАЯ ЧАСТОТА (круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n — число колебаний в 1 с., T — период колебаний. Угловая частота при вращательном движении — число оборотов, совершаемое вращающимся твердым телом за 1 с., при этом T — время, за которое совершается 1 оборот.

найдено в «Иллюстрированном энциклопедическом словаре»

(круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n — число колебаний в 1 с., T — период колебаний. Угловая частота при вращательном движении — число оборотов, совершаемое вращающимся твердым телом за 1 с., при этом T — время, за которое совершается 1 оборот.

найдено в «Естествознании. Энциклопедическом словаре»

(круговая частота), число колебаний, совершаемых за 2ПИ единиц времени. У. ч. w = 2ПИ*у = 2ПИ/Т, где v — число колебаний в единицу времени, Т — период колебаний. Обычно используемая единица времени — секунда; тогда У. ч. измеряется в рад/с.

найдено в «Большом энциклопедическом политехническом словаре»

круговая частота, циклическая частота, — хар-ка периодич. колебат. процесса. У. ч. со равна произведению частоты колебаний на 2ПИ: w = 2ПИv = 2ПИ/Т, где v и Т — частота и период колебаний. Единица У. ч. (в СИ) — рад/с (см. Радиан).

найдено в «Современном энциклопедическом словаре»

УГЛОВАЯ ЧАСТОТА (круговая частота), число колебаний, совершаемых за 2? секунд. Угловой частоты, где ? — число колебаний в секунду, Т — период колебаний.

найдено в «Большом Энциклопедическом словаре»

УГЛОВАЯ ЧАСТОТА (круговая частота) — число колебаний, совершаемых за 2? секунд. Угловой частоты , где ? — число колебаний в секунду, Т — период колебаний.

найдено в «Большом энциклопедическом словаре»

— (круговая частота) — число колебаний, совершаемых за 2?секунд. Угловой частоты , где ? — число колебаний в секунду, Т — периодколебаний.

АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
ABCDEFGHIJKLMNOPQRSTUVWXYZ

Угловая частота и частота: 3 важных объяснения

Угловая частота и частота — это величины, которые измеряют колебания в единицу времени.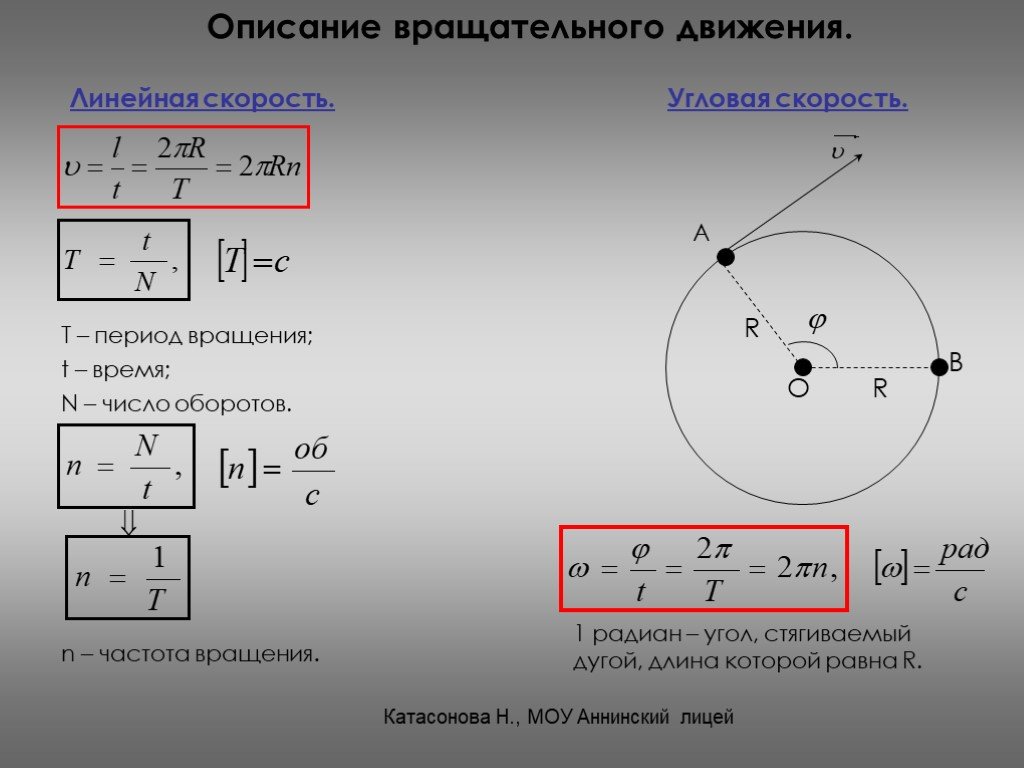 В статье обсуждается взаимосвязь между угловой частотой и частотой. 

Угловая частота описывает угловое смещение тела в единицу времени. В соотношении частота описывает количество колебаний тела в единицу времени.. Угловая частота измеряет ту же характеристику, что и частота, и обе величины являются скалярами, которые имеют только величину, но не направление.

Колеблющееся тело или генератор означает, что тело выполняет периодическое движение, выполняя один цикл; когда он проходит через диапазон позиций из своего среднего положения и снова возвращается в свое среднее положение.

Величины колеблющегося тела, такие как угловая частота, обозначенная омега символ (ω) и частота, представленная (f), Опишите частота колебаний тела или насколько оно колеблется от своего среднего положения. Но эти величины основаны на типах колебаний. Когда колебание линейное, мы исследуем его частоту. В то время как, когда он угловой, мы исследуем его угловую частоту. 

Угловая частота и частота

Поскольку частота вычисляет количество колебаний всего тела в единицу времени, единица измерения частоты представлена ​​в виде вибрация в секунду или, точнее, циклов в секунду. Проще говоря, его единица измерения Герцы (Гц) что равно одному циклу в секунду.

Чтобы определить частоту колебаний, нам сначала нужно узнать ее временной период. В временной период также количество колеблющегося тела, которое показывает общее время, затрачиваемое телом на одно колебание. Сравнивая определения как периода времени, так и частоты, эти величины колебаний обратны друг другу.

т. е. [латекс]f = \frac{1}{T}[/latex] ……….. (#)

Например, в синусоидальной форме волны время, необходимое волной для завершения одного колебания, составляет ½ секунды, затем его частота составляет 2 цикла в секунду или герц.

Угловая частота и частота
Связь частоты с периодом времени

Но когда тело колеблется под углом, его смещение от среднего положения измеряется угловой частотой. Тело движется по круговой траектории, охват определенного угла считается его угловым перемещением. Поскольку угловое смещение включает угол, угловая частота колеблющегося тела выражается в радиан в секунду (рад с-1) or оборот в минуту (об / мин).

Например, обсуждая вращение карусели в детском парке, мы выражали ее угловую частоту в радианах в минуту. Но когда мы говорим об угловой частоте вращения Луны вокруг Земли, имеет смысл выразить ее в радианах в день.  

Узнайте больше о Простое гармоническое движение угловой частоты.

Связь между частотой и угловой частотой

Частота и угловая частота колеблющегося тела связаны друг с другом, потому что обе величины используются для определения скорости колебаний тела.

Формула угловой частоты (ω) колеблющегося тела представляет собой произведение частоты (f) и угла, на который тело колеблется. т.е. [латекс]\омега = 2\pi f[/латекс]. Это означает, что угловая частота аналогична частоте с постоянным коэффициентом 2π.

Угловая частота и частота

Игровой автомат простой гармоническое движение (ШМ) системы показывает, что угловая частота ω и частота f имеют одинаковые размерности. Следовательно, обе величины измеряются одной и той же единицей обратной времени. т. е. с-1. Этот факт согласуется с единицей измерения угловой частоты. Тем не менее, это сравнивается с законами физики и устраняет разницу в соотношении между угловой частотой и частотой. т.е. [латекс]\омега = 2\pi f[/латекс].

Как и частота (f) колеблющегося тела, его угловая частота (ω) также связана с периодом времени (T). Когда тело вращается по орбитальной или просто круговой траектории, его период времени оценивает общее время, необходимое телу для завершения одного оборота.

Поскольку f = 1/T, соотношение между угловой частотой и частотой становится [латекс]\омега = \фрак{2\пи }{Т}[/латекс]. ……(*)

Связь между угловой частотой и частотой (Кредит: числовой)

Что такое 2π в угловой частоте и частоте?

Когда мы выражаем скорость колебаний через период времени, постоянный множитель 2π связывает угловую частоту с частотой.

Описывая угловую частоту, мы объясняем вращение тела в радианах в секунду. Тело должно повернуться на 360 °, чтобы совершить одно колебание. Поскольку 360 ° = 2π. Вот почему постоянный множитель 2π играет важную роль при связывании угловой частоты с частотой во время колебаний. 

Во время колебания тела от среднего положения мы просто видим насколько изменяется угол колебания тела за одну секунду. Например, если угол, под которым колеблется тело, изменяется от 0 радиан до 2p радианы (360 °) за одну секунду, мы можем определить его угловую частоту, разделив изменение угла 2π на период времени T в одну секунду в соответствии с формула (*).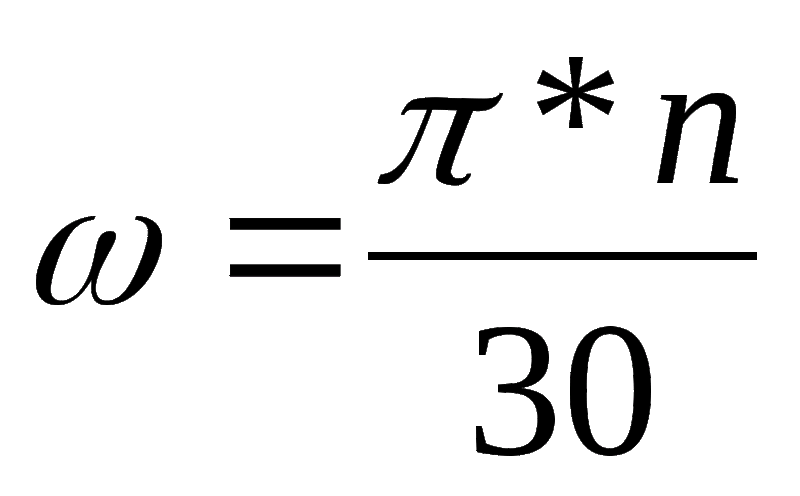 {\circ}[/latex].

Узнайте больше о Угловое уравнение движения.

Угловая частота против частоты

Угловая частота	частота
Это угловое смещение тела за единицу времени.	Это количество колебаний тела в единицу времени.
Он использует радианы для измерения частоты колебаний.	Он использует циклы для измерения частоты колебаний.
Анализируется при угловых колебаниях тела.	Анализируется при линейных колебаниях тела.
Это угловая кинематическая величина, которая объясняется с помощью только полярной системы координат.	Это линейная кинематическая величина, которая объясняется с помощью как полярной, так и декартовой систем координат.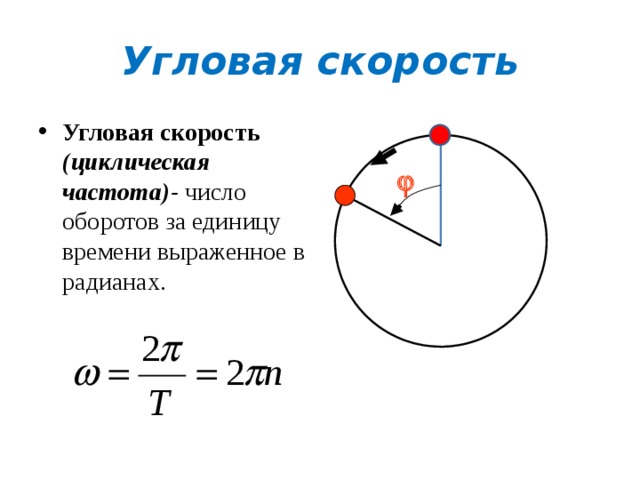
Его концепции относятся к оптике, механике и схемам переменного тока.	Его концепции относятся к акустике, электромагнитам и радиотехнике.

Калькулятор угловой частоты

Создано Михиром Кеткаром

Отзыв от доктора наук Доминика Черниа и Джека Боуотера

Последнее обновление: 01 октября 2022 г.

Содержание:

• Что такое угловая частота?
• Что такое формула угловой частоты?
• Как пользоваться калькулятором угловой частоты?

Калькулятор угловой частоты поможет вам определить угловую частоту (также известную как угловая скорость) системы. В статье ниже мы опишем как рассчитать угловую частоту для простого гармонического движения и вращательного движения , и показать различные уравнения угловой частоты.

Что такое угловая частота?

Угловая частота — это скалярная физическая величина, измеряющая скорость вращения или колебаний объекта во времени .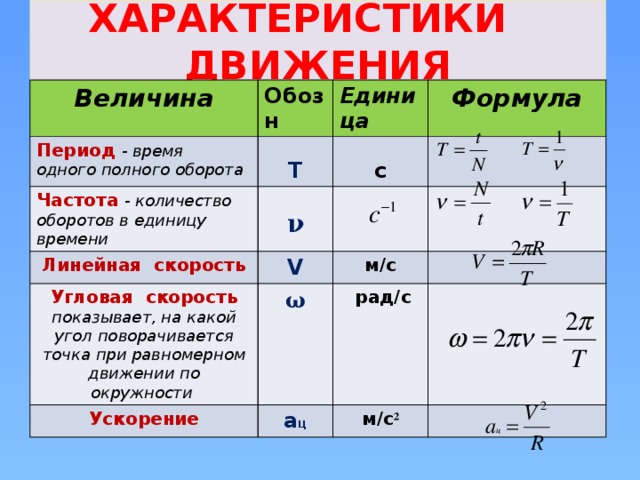 Обычно его обозначают греческими буквами Ω или ω . Мы измеряем его в радианах в секунду, единицах СИ или об/мин (оборотов в минуту). Она отличается от частоты в 2π раза. Вы можете узнать больше о частоте из нашего частотного калькулятора.

Что такое формула угловой частоты?

В зависимости от ситуации могут возникнуть вопросы типа «Как рассчитать угловую скорость колеса?» или «Какова угловая частота маятника?». Чтобы ответить на оба этих вопроса, вам нужно будет использовать разные подходы, которые мы опишем ниже:

• Как вычислить угловую частоту вращающегося объекта?

Вы можете использовать основное уравнение угловой частоты для вращающихся объектов:

ω=ΔθΔt\omega = \frac{\Delta \theta }{\Delta t}ω=ΔtΔθ​

где:

• Δθ\Delta \thetaΔθ- Количество оборотов, выраженное в радианах; и
• Δt\Delta tΔt — Время в секундах.

Например, если шина поворачивается на 200 радиан за 40 секунд, как рассчитать угловую скорость колеса?

Решение: ω = 200 радиан / 40 секунд что означает, что ω = 5 рад/с

• Как рассчитать угловую частоту простого гармонического движения ?

В этом случае мы должны использовать уравнение угловой частоты для колеблющихся объектов:

ω=2πf=2πT\omega = 2 \pi f = \frac{2 \pi}{T} ω=2πf=T2π

где:

• fff — Частота;
• ТТТ — Период времени; и
• π — Пи, математическая константа, приблизительно равная 3,142 и определяемая как отношение между длиной окружности и диаметром окружности. (Это настоящая знаменитость в области математики 😎).

Например, если маятник колеблется с частотой 2 Гц, как в этом случае найти угловую частоту?

Решение: ω = 2 * 3,142 * 2 рад/с
что означает, что ω = 12,566 рад/с

Как пользоваться калькулятором угловой частоты?

Теперь, когда у нас есть ответы на вопрос «Что такое угловая частота?» и «Как рассчитать угловую скорость?», осталось научиться пользоваться калькулятором угловой частоты. Следуйте этим простым инструкциям, и вы быстро научитесь считать!

1. Поймите, какая формула верна.

   Объект вращается как колесо? Или он качается туда-сюда, как качели? Оба эти вида движения имеют угловую частоту, но мы вычисляем их по-разному. В зависимости от ситуации решите, какую формулу угловой частоты использовать. Для вращающихся или вращающихся объектов используйте часть с маркировкой . Для вращающихся объектов , а для колебаний используйте вторую секцию под названием . Для колеблющихся объектов .

2. Запишите значения известных переменных.

   Взгляните на информацию, которая у вас есть, и на ту, которой у вас нет. Уравнение для расчета угловой скорости является линейным, поэтому изменение формулы должно быть простым.

3. Убедитесь, что вы используете правильные единицы измерения.

   Одна из самых распространенных ошибок учеников (и учителей 😜) заключается в том, что они забывают использовать соответствующие единицы измерения. Всегда проверяйте единицы измерения переменных. Используйте раскрывающееся меню в конце поля ввода, чтобы изменить единицы измерения.

   Угловая частота может быть выражена в рад/с, об/мин, имп/с или Гц. Используйте наш калькулятор cps, чтобы узнать, как конвертировать между ними.

4. Введите значения.

   Введите значения в поля и вуаля! У вас будет ответ в поле с надписью Угловая частота . Довольно аккуратно, правда?

5. Использование калькулятора в обратном порядке

   У вас уже есть угловая частота и вы хотите рассчитать какую-то другую переменную? Этот калькулятор может сделать это тоже! Просто введите значение в поле с надписью Угловая частота для расчета других переменных.

Если вам понравился этот калькулятор, обязательно ознакомьтесь с нашим калькулятором углового ускорения!

MIHIR KETKAR

для вращающихся объектов

угловое смещение

Время, взятое

угловая частота

для колеблющихся объектов

Профилак

Частота

Angular Competty

Проверьте 200003 и период.0003

Угловое ускорениеУгловое смещениеУгловой импульс… Еще 17

Угловая частота

В физике угловая частота ω (также называемая угловой скоростью, радиальной частотой, круговой частотой, орбитальной частотой и частотой в радианах) является скалярной мерой вращения оценивать. Угловая частота (или угловая скорость) есть величина векторной величины угловой скорости. Термин вектор угловой частоты \vec{\omega} иногда используется как синоним векторной величины угловой скорости.[1]

Один оборот равен 2π радианам, следовательно[1][2]

\( \omega = {{2 \pi} \over T} = {2 \pi f} = \frac {|v|} { |r|} , \)

где

ω — угловая частота или угловая скорость (измеряется в радианах в секунду),
T — период (измеряется в секундах), 90 182
f — обычная частота (измеряется в герцах) (иногда обозначается буквой ν), 90 182
v — тангенциальная скорость точки относительно оси вращения (измеряется в метрах в секунду),
r — радиус вращения (измеряется в метрах).

Единицы

В единицах СИ угловая частота обычно выражается в радианах в секунду, даже если она не выражает значение вращения. С точки зрения размерного анализа единица измерения Герц (Гц) также является правильной, но на практике она используется только для обычной частоты f и почти никогда для ω. Это соглашение помогает избежать путаницы.[3]

При цифровой обработке сигналов угловая частота может быть нормализована частотой дискретизации, что дает нормализованную частоту. 9{2} = \frac{k}{m} , \)

, где

k — жесткость пружины
m — масса объекта.

Это называется собственной частотой (которую иногда можно обозначить как ω0).
LC Circuits

Резонансная угловая частота в LC-цепи равна квадратному корню обратного значения емкости (C измеряется в фарадах), умноженному на индуктивность цепи (L в генри).[5]

\( \omega = \sqrt{1 \over LC} \) 9Нахви, Махмуд; Администратор, Джозеф (2003). Очерк теории и проблем электрических цепей Шаума. McGraw — Hill Companies (Макгроу — Хилл Профессионал). стр. 214, 216. ISBN 0-07-139307-2 .(LC1)

Связанное чтение:

Оленик, Ричард П.; Апостол, Том М .; Гудштейн, Дэвид Л. (2007). Механическая Вселенная.