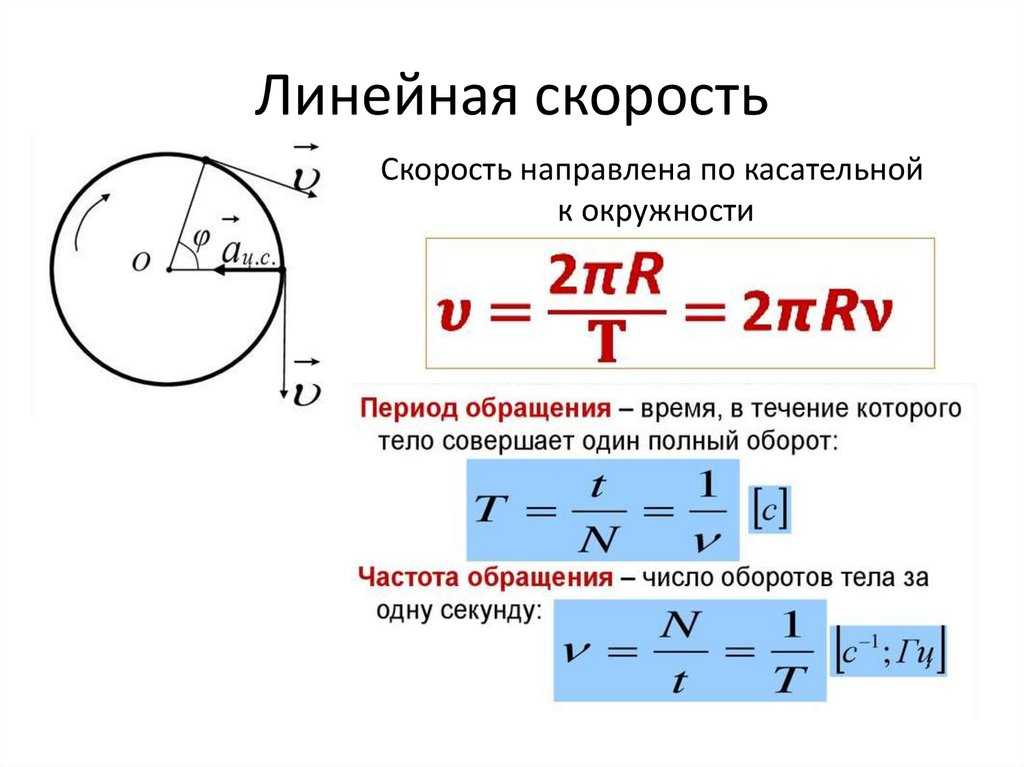
1. Формула, связывающая линейную и угловую скорости движения тела a  = 2πν

ФИЗИКА 1. Формула, связывающая линейную и угловую скорости движения тела A)  = 2πν. B) . C) . D)  = R. E) . 2. На тело массой 500 г, движущееся с ускорением 2 м/с2, действует сила A) 1000 Н B) 1 Н C) 10 Н D) 250 Н E) 100 Н 3. Кинетическая энергия тела массой 10 кг, имеющего скорость 36 км/час A) 500 Дж B) 12960 Дж C) 5000 Дж D) 180 Дж E) 360 Дж 4. Тело сохраняет свой объем, но легко меняет форму в состоянии A) газообразном. B) жидком и твердом. C) твердом. D) жидком. E) жидком и газообразном. 5. Температуре 4К по шкале Цельсия соответствует A) 40 С. B) -2690 С. C) 2690 С. D) -40 С. E) 2770 С. 6. Если напряженность электрического поля на внешней поверхности проводника равна Е0, то напряженность Е внутри проводника будет A) Е > Е0 B) Е = 0 C) Е = 2Е0 D) Е = Е0 E) Е 0 7. При прохождении по металлическому проводнику переменного электрического тока наблюдаются следующие действия 1) проводник нагревается; 2) изменяется химический состав проводника; 3) вокруг проводника появляется магнитное поле; 4) проводник укорачивается. A) 1, 2, 3, 4. B) 1, 2, 3. C) 1, 3. D) 2, 3, 4. E) 1, 3, 4. 8. Проводник с током 2А длиной 2 м находится в магнитном поле с индукцией 1Тл .Если угол наклона проводника к линиям индукции 30, то на проводник действует сила A) 4 Н. B) 1 Н. C) 2 Н. D) 3 Н. E) 5 Н. 9. За 4 с маятник совершает 8 колебаний. Частота колебаний A) 2 Гц. B) 4 Гц. C) 8 Гц. D) 0,5 Гц. E) 0,25 Гц. 10. Для связи с космическими станциями применяют волны A) ультракороткие. B) средние. C) низкой частоты. D) короткие. E) длинные. 11. Согласно гипотезе Планка, абсолютно черное тело излучает энергию A) непрерывно. B) не излучает. C) при высоких температурах непрерывно, а при низких — порциями. D) порциями. E) при высоких температурах порциями, а при низких — непрерывно. 12. Энергия фотона, поглощаемого фотокатодом, равна 5 эВ. Работа выхода электрона из фотокатода равна 2 эВ. Найдите величину задерживающего потенциала, при котором прекратился фототок (е = 1,610-19 Кл). A) 7 В. B) 3 В. C) 3,5 В. D) 10 В. E) 2,5 В. 13. Энергия покоя электрона (me=9,1·10-31 кг; с=3∙108 м/с). A) 8,1910-12 Дж. B) 8,1910-14 Дж. C) 8,1910-16 Дж. D) 8,1910-15 Дж. E) 8,1910-13 Дж. 14. Число протонов в ядре равно A) числу электронов в оболочке нейтрального атома. B) A-Z. C) A+Z. D) числу нейтронов в ядре. E) массовому числу А. 15. При ядерной реакции освобождается A) . B) . C) . D) . E) . 16. Поезд за 20 с достиг скорости 25 м/с, двигаясь с ускорением 0,2 м/с2. За это время он прошел путь A) 460 м. B) 810 м. C) 1440 м. D) 1960 м. E) 2000 м. 17. Площадь меньшего поршня гидравлического пресса 10 . На него действует сила 200 Н. Площадь большего поршня 200 . При этом на большой поршень действует сила A) 40 кН. B) 4 Н. C) 4 кН. D) 400 кН. E) 400 Н. 18. Вагонетку массой 2т по горизонтальному пути человек равномерно перемещает на 100м. Если коэффициент трения 0,01, то на этом пути человек совершает работу (g = 10 м/с2) A) 200 кДж. B) 20 кДж. C) 2 кДж. D) 0,2 кДж. E) 20 Дж. 19. Космический корабль массой 50000 кг имеет реактивный двигатель с силой тяги 105 Н. Двигатель работал 6 с. Скорость корабля изменилась на A) 1,210-2 м/с. B) 1,210-2 м/мин. C) 12 м/с. D) 12 м/мин. E) 0,2 м/с. 20. Материальная точка летит в направлении неподвижной стенки со скоростью , перпендикулярной стенке. Происходит абсолютно упругий удар. Изменение проекции импульса точки на ось X A) 0. B) 2m. C) –2m. D) –m. E) m. 21. Мяч массой 0,5 кг брошен вертикально вверх со скоростью 10. Если сопротивлением воздуха перенебречь, то на высоте 4 м мяч обладает кинетической энергией равной A) 10 Дж B) 5 Дж C) –5 Дж D) 0 E) –10 Дж 22. Удельная теплота плавления свинца 22,6 кДж/Кг. Для того чтобы расплавить за 10 мин 60 кг свинца, взятого при температуре плавления, мощность нагревателя должна быть A) 2,26 кВт B) 13500 кВт C) 0,226 Вт D) 226 Вт E) 81300 кВт 23. Внутренняя энергия 4 моль одноатомного идеального газа при уменьшении его температуры на 200 К изменится на (R = 8,31 Дж/(моль·К) A) ≈5 кДж . B) ≈25 кДж. C) ≈15 кДж. D) ≈10 кДж. E) ≈20 кДж. 24. Идеальный газ переходит из состояния 1 в состояние 2 в процессе, представленном на диаграмме р – V. В этом процессе A) газ совершил работу 200 Дж. B) работа равна нулю. C) газ совершил работу 400 Дж. D) внешние силы совершили работу над газом 200 Дж. E) внешние силы совершили работу над газом 400 Дж. 25. Чтобы получить энергию Q = Дж, нужно сжечь каменного угля (q = Дж/кг) A) кг. B) кг. C) кг. D) кг. E) кг. 26. При постоянном давлении 105 Па объем воздуха, находящегося в помещении, увеличился на 200 дм3. При этом газ совершил работу A) 2·104Дж B) 2·106Дж C) 2·105Дж D) 20Дж E) 5·106 Дж 27. Конденсатор отключен от источника. Если удвоить заряд на каждой из пластин конденсатора, то его энергия A) увеличится в 2 раза. B) увеличится в 4 раза. C) не изменится. D) увеличится в 8 раз. E) увеличится в 16 раз. 28. — частица, влетевшая в магнитное поле со скоростью 106 м/с, движется по траектории с радиусом кривизны 1,038 м. Индукция магнитного поля равна ( кг; Кл) A) 2,5 мТл. B) 20 мТл. C) 5 мТл. D) 0,4 Тл. E) 10 мТл. 29. Движение математического маятника задано уравнением x = 0,1cos(2t+). Период его колебаний равен A) 2 c. B) 1 c. C) D)  c. E) 0,1 c. 30. Если электрическую емкость конденсатора уменьшить в 2 раза, то емкостное сопротивление A) увеличится в 2 раза. B) увеличится в 4 раза. C) уменьшится в 2 раза. D) уменьшится в 4 раза. E) не изменится. 31. Перед вертикально поставленным плоским зеркалом стоит человек. Если человек приблизится к плоскости зеркала на 1 м, то расстояние между человеком и его изображением A) увеличится на 2 м. B) уменьшится на 1 м. C) уменьшится на 2 м. D) не изменится.н E) уменьшится на 0,5 м. 32. Предмет находится между фокусом и двойным фокусом рассеивающей линзы. При этом будет наблюдаться изображение A) перевернутое, увеличенное, мнимое. B) прямое, увеличенное, мнимое. C) прямое, увеличенное, действительное. D) прямое, уменьшенное, мнимое. E) перевернутое, уменьшенное, действительное. 33. Частота фотона, излучаемого при переходе атома из возбужденного состояния с энергией Е1 в основное состояние с энергией Е0, равна A) . B) . C) . D) . E) . 34. Трамвай, двигаясь от остановки равноускоренно, прошел путь 30 м за 10 с. В конце пути он приобрел скорость A) 3 м/с B) 7,5 м/с C) 9 м/с D) 6 м/с E) 4,5 м/с 35. Наклонившись под углом 600 к горизонту, конькобежец описал окружность радиусом 20 м. Его скорость равна (; ) A) 25 м/с. B) 11 м/с. C) 5 м/с. D) 15 м/с. E) 19 м/с 36. При подвешивании груза массой 2 кг пружина удлиняется на 4 см. Работа, совершенная при удлинении ее от 2 до 12 см, равна A) 2,5 Дж. B) 3,5 Дж. C) 3,8 Дж. D) 3,6 Дж. E) 3 Дж. 37. На глубине 40 м в стоячей воде пузырек воздуха имеет объем 3 мм3. Объем этого же пузырька при подъеме его на поверхность воды равен (процесс считать изотермическим, атмосферное давление 105 Па). A) 15 мм3 B) 120 мм3 C) 60 мм3 D) 24 мм3 E) 12 м3 38. Электрон, пролетевший ускоряющую разность потенциалов 100В обладает скоростью ( е = 1,6·10-19 Кл; m = 9·10-31 кг) A) 3 км/с. B) 3·106 м/с. C) 6·106 м/с. D) 6 км/с. E) 106 м/с. 39. При электролизе раствора серной кислоты за 1 час выделилось 0,3 г водорода. Если сопротивление его 0,4 Ом, а электрохимический эквивалент водорода 0,01·10-6 кг/Кл, то мощность, расходуемая на нагревание электролита A) ≈45 Вт. B) ≈20 Вт. C) ≈26 Вт. D) ≈50 Вт. E) ≈150 Вт. 40. При гармонических колебаниях вдоль оси ox координата тела изменяется по закону x = 0,4 sin2t (м). Модуль амплитуды ускорения равна A) 0,4 м/с2 . B) 1,6 м/с2. C) 0,1 м/с2 . D) 0,8 м/с2 . E) 0,2 м/с2.

Равномерное движение по прямой и вращение по окружности. Связь угловой и линейной скорости

Раздел физики, который изучает движение тел по различным траекториям, называется кинематикой. Практически полезными типами перемещения объектов являются движение по прямой и по окружности. Рассмотрим в статье, что представляют собой эти типы движения, какими формулами они описываются, а также приведем связь угловой и линейной скорости.

Движение по прямой

Связь угловой и линейной скорости можно определить, если знать, о каких величинах идет речь. Начнем со скорости линейной.

Со школьной скамьи каждый знает, что перемещение объектов в пространстве характеризуется тремя главными величинами:

• пройденный путь S;
• время движения t;
• скорость v.

Формула, связывающая в единое равенство названные величины, приведена ниже:

S = v * t.

Приведенное выражение описывает равномерное движение тела по прямой линии. В международной системе единиц СИ величина S измеряется в метрах (м), t — в секундах (с), v — в метрах в секунду (м/с). Помимо названных единиц, путь и время могут измеряться в километрах (км) и часах (ч), соответственно. Тогда скорость будет выражаться в километрах в час (км/ч).

Записанная формула может применяться для решения широкого круга практических задач, например, движение транспортных средств по дорогам, движение кораблей и лодок по рекам, полет птиц и так далее.

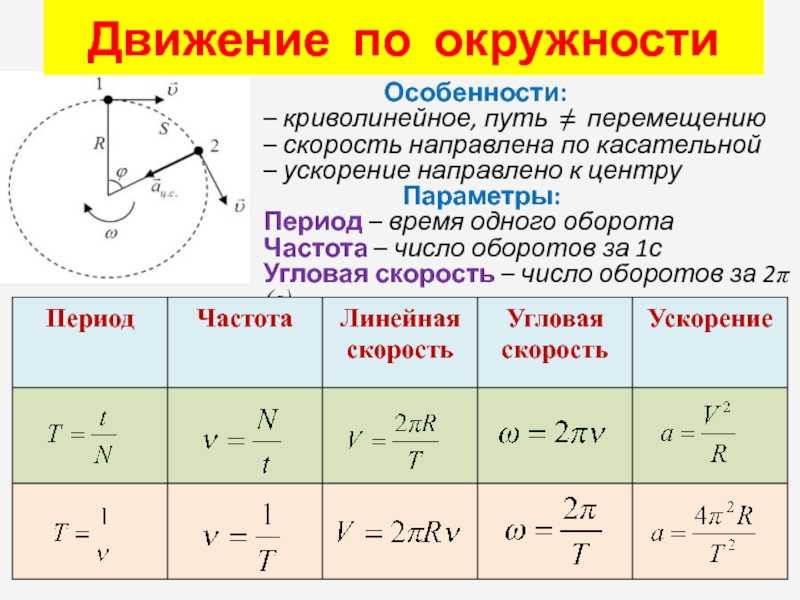
Движение по окружности

Перед тем как перейти к выводу формулы связи линейной и угловой скорости, следует рассмотреть последнюю с точки зрения физики.

Угловая скорость появляется в физике, когда речь идет о вращающихся объектах. Примерами могут быть вращение колеса велосипеда, маховика автомобиля или планеты вокруг своей звезды. Угловая скорость тела показывает, на какой угол в радианах оно поворачивается за единицу времени. Обычно эту величину обозначают греческой буквой ω (омега). Она измеряется в радианах в секунду (рад/с).

По аналогии с линейным случаем можно назвать три главных величины, которые описывают движение по окружности с постоянной скоростью угловой:

• угол поворота θ;
• время t;
• угловая скорость ω.

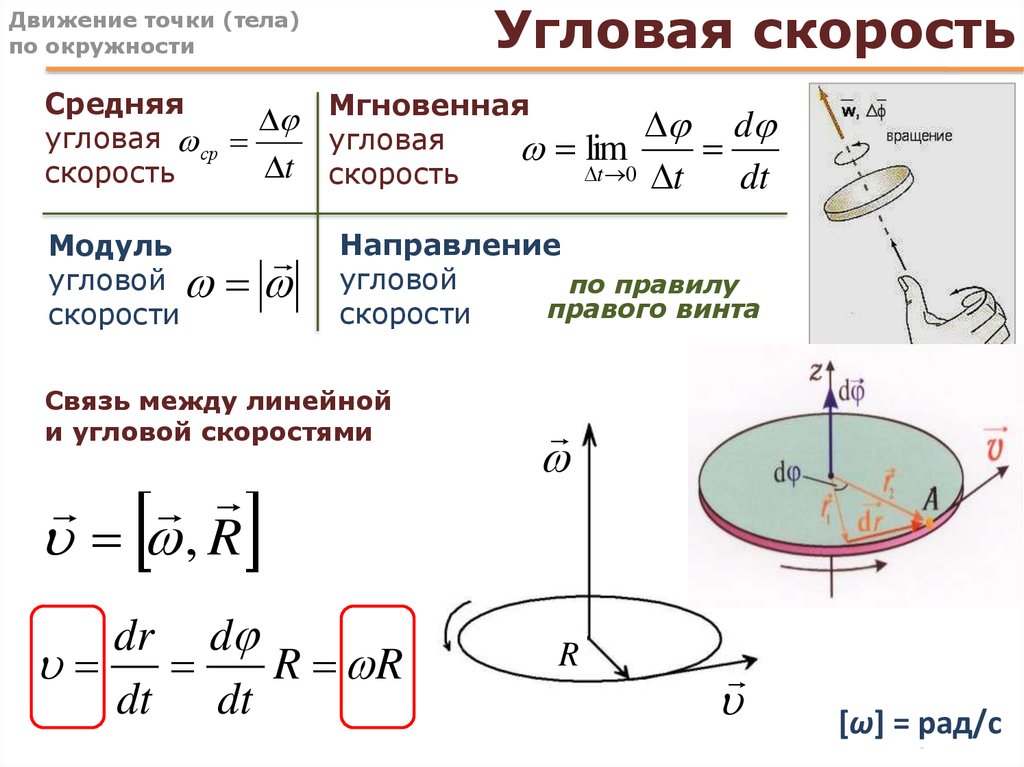
Соответствующая формула, которая связывает эти величины, выглядит так:

θ = ω * t.

Угол поворота тела θ вокруг оси вращения измеряется в радианах. Напомним, что окружность имеет 2 * pi радиан (около 6,28). Если полученное по формуле значение θ оказалось больше, чем 2 * pi, то это означает, что тело сделало больше одного оборота вокруг оси.

Таким образом, записанное выражение позволяет рассчитать число оборотов, совершаемых телом за известный промежуток времени t.

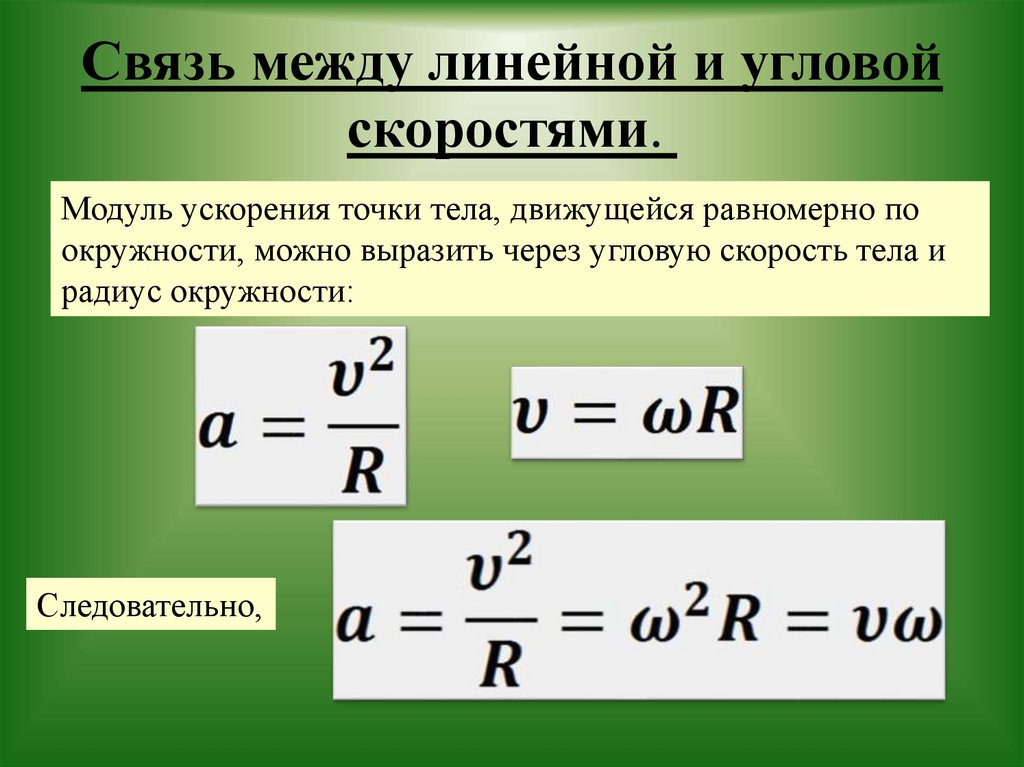
Связь угловой и линейной скорости

Теперь можно рассмотреть этот вопрос. Предположим, что тело, имеющее линейную скорость v, вращается по окружности радиусом R. Чтобы получить между линейной и угловой скоростью связь, рассмотрим, какое время понадобится телу, чтобы сделать полный один оборот. Поскольку пройденный путь будет равен длине окружности, то следующее выражение будет справедливым:

t = S/v = 2 * pi * R/v.

Теперь воспользуемся угловыми величинами. За найденное время одного оборота t, тело повернется точно на 2 * pi радиан. Последнее означает, что его угловая скорость будет равна:

ω = θ/t = 2 * pi/t.

Подставим рассчитанное выше время t и получим между угловой и линейной скоростью связь:

ω = 2 * pi/t = 2 * pi/(2 * pi * R/v) = v/R.

Полученную формулу можно записать в двух видах:

ω = v/R;

v = ω * R.

Каждое из выражений применяется в зависимости от того, какая величина в условии задачи известна. Формулы позволяют сделать важный вывод: чем больше радиус орбиты вращение, тем больше будет линейная скорость при постоянной угловой скорости.

Далее решим интересную задачу на применение полученных формул.

Что быстрее — Земля или Марс?

Известно, что Земля и Марс являются 3-й и 4-й планетами Солнечной системы, соответственно. Обе планеты движутся приблизительно по круглым орбитам. Расстояние от нашей звезды до Земли равно 149 597 870,691 км, а один оборот вокруг нее она делает за 365,256 дней.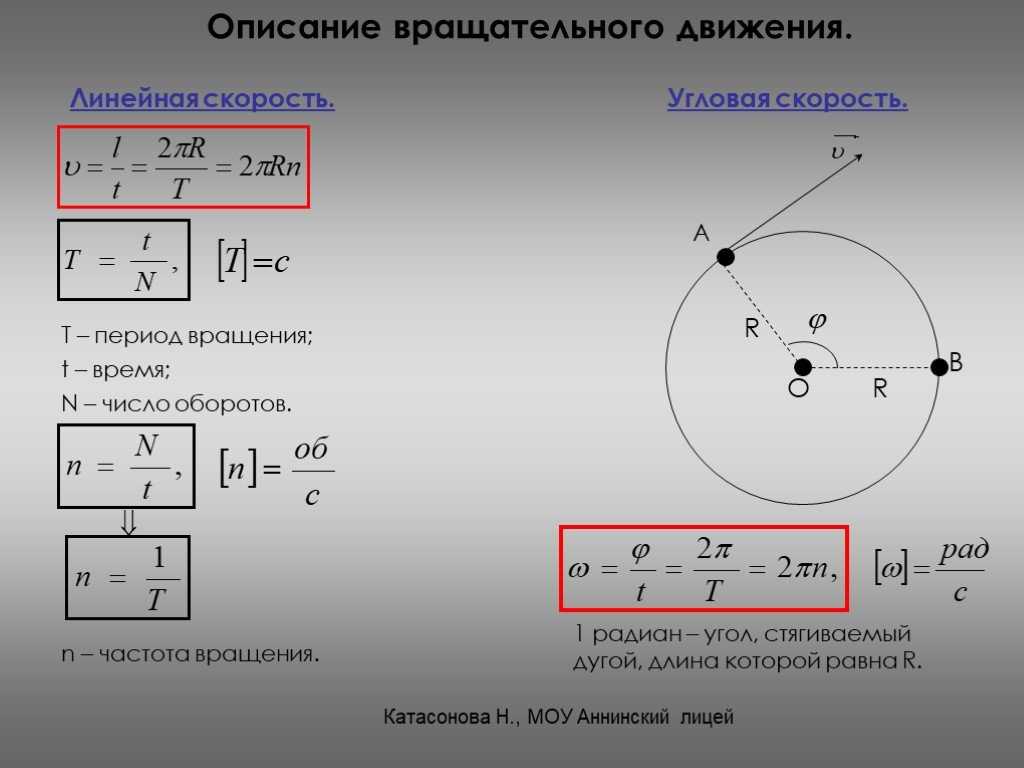 Марс расположен от Солнца на расстоянии 227 936 640 км, и один оборот вокруг него делает за 686,971 земных дня. Необходимо определить и сравнить линейные скорости планет.

Угловая скорость планеты может быть рассчитана по формуле:

ω = 2 * pi/T.

Где T — период (время совершения одного оборота вокруг звезды). Подставляя ω в формулу для v, получаем:

v = 2 * pi * R/T.

Переведем время оборота планет в часы и подставим данные в это равенство, получим:

• для Земли: v = 2 * 3,14 * 149597870,691/(365,256 * 24) ≈ 107,2 тыс. км/ч;
• для Марса: v = 2 * 3,14 * 227936640/(686,971 * 24) ≈ 86,8 тыс. км/ч.

Обе цифры являются огромными. Так, Земля за один час пролетает в космосе расстояние, практически равное трем ее окружностям по экватору. Полученные скорости свидетельствуют, что Земля движется быстрее Марса, и ее скорость на 24 % больше марсианской.

7.1: Линейная и угловая скорость

1. Последнее обновление

2. Сохранить как PDF

• Тимон Идема
• Делфтский технологический университет через TU Delft Open

Мы связали линейную и угловую скорости вращающегося объекта в двух измерениях в разделе 5. 1. Там мы также уже установили соотношение между вектором линейной скорости и вектором вращения в трех измерениях (уравнение 5.1.5):

\[\boldsymbol{v}=\boldsymbol{\omega} \times \boldsymbol{r}\]

Нетрудно заметить, что это выражение действительно упрощается до скалярного соотношения \(v = \omega r\) для вращений на плоскости с правильным знаком для линейной скорости. Однако это вряд ли является доказательством, так что давайте поставим это на более прочную основу. Предположим, \(\boldsymbol{r}\) образует угол \(\phi\) с \(\boldsymbol{\omega}\). Предположим также, что он изменяется на \(\mathrm{d}\boldsymbol{r}\) за интервал времени \(\mathrm{d}t\), тогда, если мы имеем чистое вращение, \(\mathrm{d}\ boldsymbol{r}\) перпендикулярен как к \(\boldsymbol{r}\), так и к \(\boldsymbol{\omega}\), а его величина определяется выражением \(|d \boldsymbol{r}| = \omega r \sin \phi \mathrm{d} t=|\boldsymbol{\omega} \times \boldsymbol{r}| \mathrm{d} t\), где \(\omega\) и \(r\) длины их соответствующих векторов. Наконец, если смотреть сверху (т.е. если смотреть на вектор \(\boldsymbol{\omega}\)) вращение должно быть против часовой стрелки (по определению направления \(\boldsymbol{\omega}\) ), что соответствует направлению \(\boldsymbol{\omega} \times \boldsymbol{r}\). Таким образом, мы обнаруживаем, что и величина, и направление \(\boldsymbol{v}=\mathrm{d} \boldsymbol{r} / \mathrm{d} t\) действительно равны \(\boldsymbol{\omega} \times \ жирныйсимвол{r}\), и уравнение 5.1.5 выполняется.

Эта страница под названием 7.1: Linear and Angular Velocity распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Тимоном Идема (TU Delft Open) через исходный контент, отредактированный в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Тимон Идема

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. угловая скорость
   2. источник@https://textbooks. open.tudelft.nl/textbooks/catalog/book/14

Угловая и линейная скорость — предварительный расчет

Все ресурсы по предварительному расчету

12 диагностических тестов
380 практических тестов
Вопрос дня
Карточки
Учитесь по концепции

← Предыдущая 1 2 Следующая →

Предварительное исчисление Справка »
Тригонометрические функции »
Угловая и линейная скорость

Если мяч движется по окружности диаметром  со скоростью , найдите угловую скорость мяча.

Возможные ответы:

Правильный ответ:

Объяснение:

Используя уравнение,

  где

=угловая скорость, =линейная скорость и =радиус окружности.

В данном случае радиус равен 5 (половина диаметра), а линейная скорость равна 20 м/с.

.

Сообщить об ошибке

Предположим, что автомобильная шина совершает оборот  раз в секунду. Шина имеет диаметр  дюймов. Найдите угловую скорость в радианах в секунду.

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу для угловой скорости.

Частота шины 8 оборотов в секунду. Радиус не используется.

Подставьте частоту и решите.

Сообщить об ошибке

Какова угловая скорость волчка, если он перемещается в радианах за треть секунды?

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу для средней скорости.

Единицы измерения омеги — радианы в секунду.

Подставьте данные и найдите омегу.

Сообщить об ошибке

Диаметр шины на автомобиле делает  оборотов в секунду. Найдите угловую скорость автомобиля.

Возможные ответы:

Правильный ответ:

Объяснение:

Напомним, что  .

Так как шина вращается 9,3 раза в секунду, кажется, что шина будет вращаться

 или .

Мы используем  , чтобы указать, что шина вращается на 360 градусов или радианов за каждый оборот (как и должно быть).

Таким образом, 

 ваш окончательный ответ.

Обратите внимание, что радианы — это ПРОСТО другой способ записи градусов. Все более высокие числа в ответах выше — это измерения фактической линейной скорости шины, а не угловой скорости.

Сообщить об ошибке

Колесо автомобиля радиусом 20 дюймов вращается на шоссе со скоростью 8 оборотов в секунду. Чему равна угловая скорость шины?

Возможные ответы:

Ни один из этих ответов.

Правильный ответ:

Объяснение:

Угловая скорость аналогична линейной скорости, но вместо расстояния в единицу времени используются градусы или радианы. Любой движущийся объект имеет как линейную, так и угловую скорость (хотя объекты имеют угловую скорость только при вращении).

Поскольку наша шина совершает 8 оборотов в секунду, мы умножаем на  , поскольку полный оборот (360°) равен .

Сообщить об ошибке

Самолет летит на северо-восток. Если восточная составляющая его скорости равна , с какой скоростью движется самолет?

Возможные ответы:

Ни один другой ответ

Пояснение:

Поскольку самолет движется на северо-восток, мы знаем, что он движется под углом 45 градусов к северу от востока. Поэтому мы можем изобразить это на диаграмме:

У нас есть вся информация, необходимая для определения скорости самолета. У нас есть угол и сторона, примыкающая к этому углу. Следовательно, мы можем использовать функцию косинуса для определения скорости.

Переставляя v, получаем:

Сообщить об ошибке

Автомобиль движется на северо-запад со скоростью  м/ч. Каковы величины каждой из его северной и западной составляющих?

Возможные ответы:

Север: MPH

Запад: MPH

Север: MPH

Запад: MPH

Север: MPH

Запад: MPH

Север: MPH

West: MPH

.

Правильный ответ:

Север: м/ч

Запад: м/ч

Объяснение:

Если автомобиль движется на северо-запад, это означает, что угол  на  градусов выше оси x.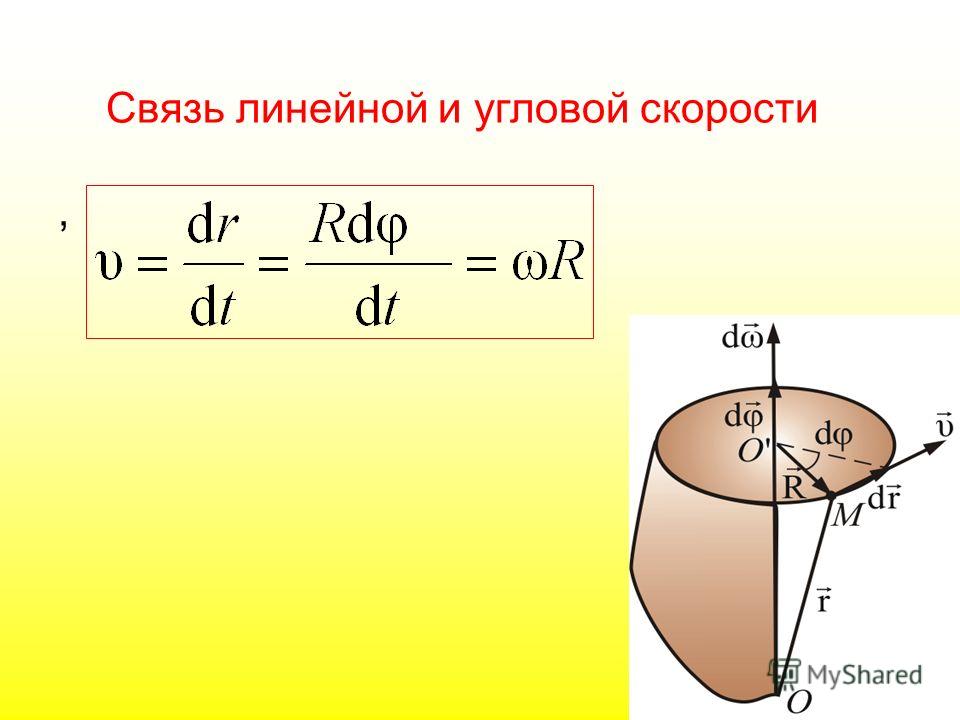 Используя этот угол и тот факт, что величина скорости равна милям в час, мы можем найти компоненты x и y или компоненты запада и севера, используя тригонометрию.

Сообщить об ошибке

Объект движется по круговой траектории. Как изменится его линейная скорость, если диаметр окружности уменьшить вдвое?

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу линейной скорости.

Диаметр в два раза больше радиуса.

Если диаметр уменьшился наполовину, радиус также уменьшится наполовину.

Следовательно:

Линейная скорость уменьшится вдвое.

Сообщить об ошибке

Найдите линейную скорость объекта в метрах в секунду, если на преодоление расстояния в  километры ушло несколько часов. Округлите до ближайшего целого числа.

Возможные ответы:

Правильный ответ:

Пояснение:

Запишите формулу линейной скорости.

Поскольку ответ требуется в метрах в секунду, потребуется сделать два преобразования.

Преобразовать 30 километров в метры.

Преобразование 2 часов в секунды.

Применить формулу.

Сообщить об ошибке

Секундная стрелка часов длинная. Найдите линейную скорость конца этой секундной стрелки.

Возможные ответы:

Ни один из других ответов.

Правильный ответ:

Объяснение:

Линейная скорость определяется как расстояние за период времени. Например, если человек пробежал 1 милю или примерно 1600 метров за 7 минут, он преодолел бы около 230 метров в минуту. Предположим, этот человек бегал по дорожке. Мы также можем измерить их скорость по центральному углу и представить их скорость как количество градусов (или радианов), которые они пробежали за единицу времени. Это считается угловой скоростью. Прекрасным примером того и другого являются стрелки на часах. Существует связь между длиной дуги, которую мы обозначаем s, радиусом r и углом  (тета). Отношения есть. Таким образом, длина дуги (s) равна радиусу окружности, на которой находится дуга, и той части круговой диаграммы, которую она покрывает (это сродни тому, на сколько градусов наш бегун пробежал «сквозь» или вокруг). Таким образом, если бы нам нужна была линейная скорость по кругу, мы могли бы сказать  или . Основные измерения, которые вам необходимо знать, — это количество градусов в окружности, из которых 360 или . Прежде чем следовать приведенному ниже пошаговому решению, вернитесь назад и посмотрите, сможете ли вы использовать эту новую информацию для получения правильного ответа.