Угловое перемещение, угловая скорость, угловое ускорение, их связь

с
линейными величинами.

Угловое
перемещение —
векторная величина, характеризующая
изменение угловой координаты в процессе
её движения.

Углова́я
ско́рость
— векторная физическая величина,
характеризующая скорость вращения
тела. Вектор угловой скорости по величине
равен углу поворота тела в единицу
времени:

,

а
направлен по оси вращения согласно
правилу буравчика, то есть, в ту сторону,
в которую ввинчивался бы буравчик с
правой резьбой, если бы вращался в ту
же сторону.

Единица
измерения угловой скорости, принятая
в системах СИ и СГС) — радианы в секунду.
(Примечание: радиан, как и любые единицы
измерения угла, — физически безразмерен,
поэтому физическая размерность угловой
скорости — просто [1/секунда]). В технике
также используются обороты в секунду,
намного реже — градусы в секунду, грады
в секунду. Пожалуй, чаще всего в технике
используют обороты в минуту — это идёт
с тех времён, когда частоту вращения
тихоходных паровых машин определяли,
просто «вручную» подсчитывая число
оборотов за единицу времени.

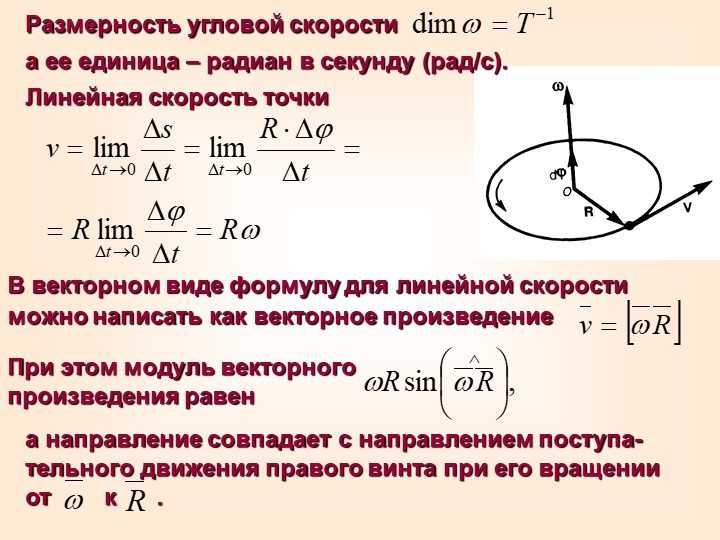
Вектор
(мгновенной) скорости любой точки
(абсолютно) твердого тела, вращающегося
с угловой скоростью

определяется формулой:

где

— радиус-вектор к данной точке из начала
координат, расположенного на оси вращения
тела, а квадратными скобками обозначено
векторное произведение. Линейную
скорость (совпадающую с модулем вектора
скорости) точки на определенном расстоянии
(радиусе) r от оси вращения можно считать
так: v = rω. Если вместо радианов применять
другие единицы углов, то в двух последних
формулах появится множитель, не равный
единице.

В
случае плоского вращения, то есть когда
все векторы скоростей точек тела лежат
(всегда) в одной плоскости («плоскости
вращения»), угловая скорость тела всегда
перпендикулярна этой плоскости, и по
сути — если плоскость вращения заведомо
известна — может быть заменена скаляром
— проекцией на ось, ортогональную
плоскости вращения. В этом случае
кинематика вращения сильно упрощается,
однако в общем случае угловая скорость
может менять со временем направление
в трехмерном пространстве, и такая
упрощенная картина не работает.

Производная
угловой скорости по времени есть угловое
ускорение.

Движение
с постоянным вектором угловой скорости
называется равномерным вращательным
движением (в этом случае угловое ускорение
равно нулю).

Угловая
скорость (рассматриваемая как свободный
вектор) одинакова во всех инерциальных
системах отсчета, однако в разных
инерциальных системах отсчета может
различаться ось или центр вращения
одного и того же конкретного тела в один
и тот же момент времени (то есть будет
различной «точка приложения» угловой
скорости).

В
случае движения одной единственной
точки в трехмерном пространстве можно
написать выражение для угловой скорости
этой точки относительно выбранного
начала координат:

,
где
— радиус-вектор точки (из начала
координат),

— скорость этой точки.

—
векторное произведение,

— скалярное произведение векторов.
Однако эта формула не определяет угловую
скорость однозначно (в случае единственной
точки можно подобрать и другие векторы
,
подходящие по определению, по другому
— произвольно — выбрав направление
оси вращения), а для общего случая (когда
тело включает более одной материальной
точки) — эта формула не верна для угловой
скорости всего тела (так как дает разные
для каждой точки, а при вращении абсолютно
твёрдого тела по определению угловая
скорость его вращения — единственный
вектор). При всём при этом, в двумерном
случае (случае плоского вращения) эта
формула вполне достаточна, однозначна
и корректна, так как в этом частном
случае направление оси вращения заведомо
однозначно определено.

В
случае равномерного вращательного
движения (то есть движения с постоянным
вектором угловой скорости) декартовы
координаты точек вращающегося так тела
совершают гармонические колебания с
угловой (циклической) частотой, равной
модулю вектора угловой скорости.

При
измерении угловой скорости в оборотах
в секунду (об/с), модуль угловой скорости
равномерного вращательного движения
совпадает с частотой вращения f, измеренной
в герцах (Гц)

(то
есть в таких единицах

).

В
случае использования обычной физической
единицы угловой скорости — радианов в
секунду

—
модуль угловой скорости связан с частотой
вращения так:

Наконец,
при использовании градусов в секунду
связь с частотой вращения будет:

Углово́е
ускоре́ние
— псевдовекторная физическая величина,
характеризующая быстроту изменения
угловой скорости твёрдого тела.

При
вращении тела вокруг неподвижной оси,
угловое ускорение по модулю равно:

Вектор
углового ускорения α направлен вдоль
оси вращения (в сторону
при ускоренном вращении и противоположно
— при замедленном).

При
вращении вокруг неподвижной точки
вектор углового ускорения определяется
как первая производная от вектора
угловой скорости ω по времени, то есть

,

и
направлен по касательной к годографу
вектора
в соответствующей его точке.

Существует
связь между тангенциальным и угловым
ускорениями:

где
R — радиус кривизны траектории точки в
данный момент времени. Итак, угловое
ускорении равно второй производной от
угла поворота по времени или первой
производной от угловой скорости по
времени. Угловое ускорение измеряется
в рад/сек2 .

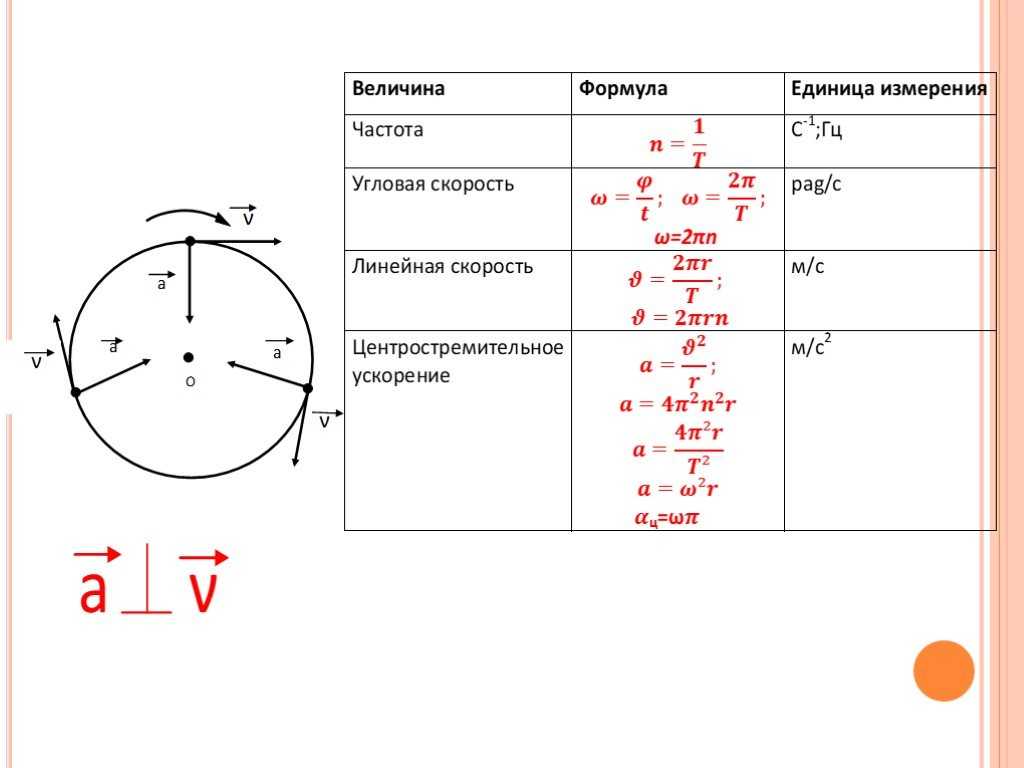
Движение по окружности с постоянной по модулю скоростью

Понятия и определения

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории.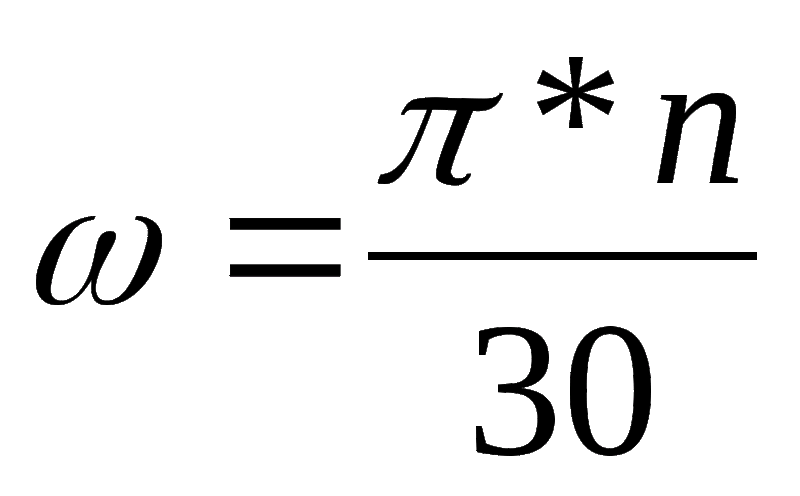 Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

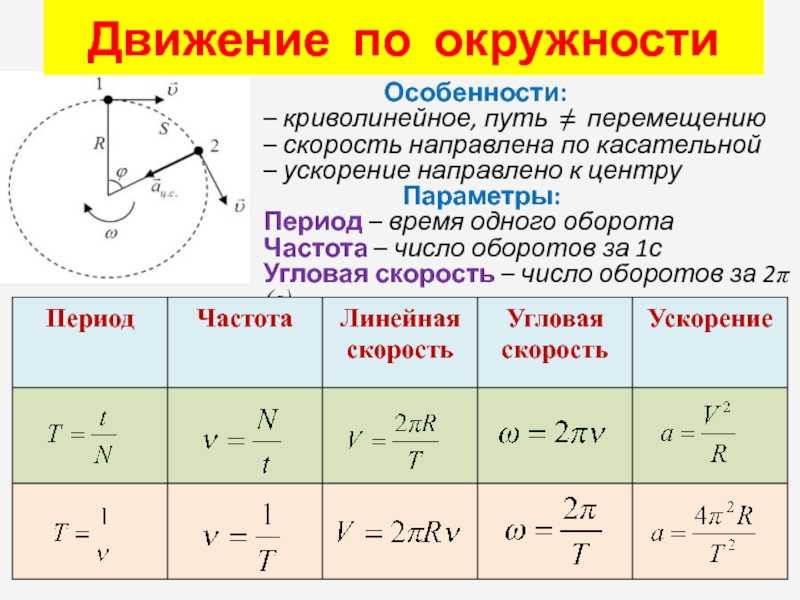
Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

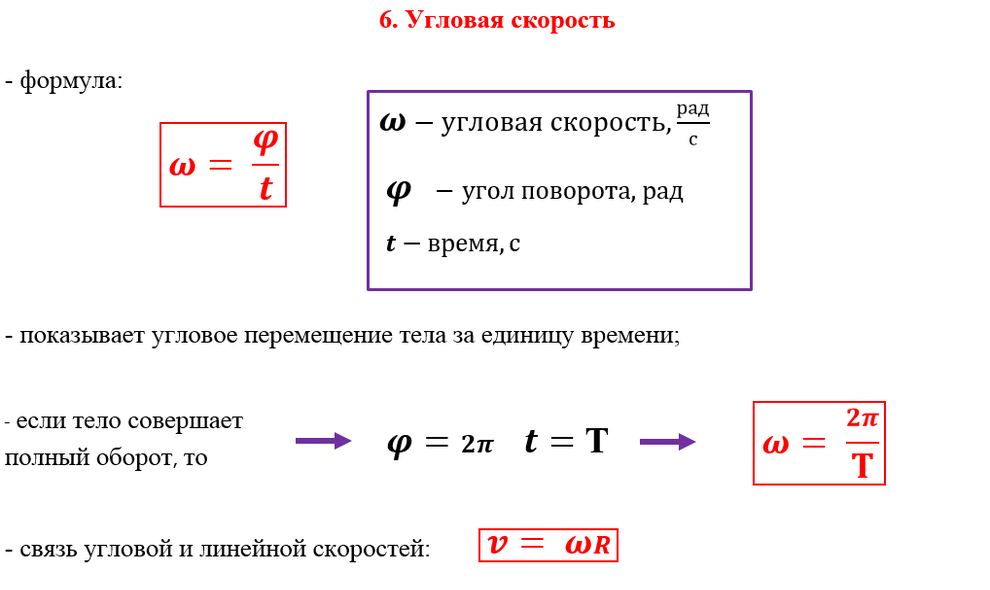
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот.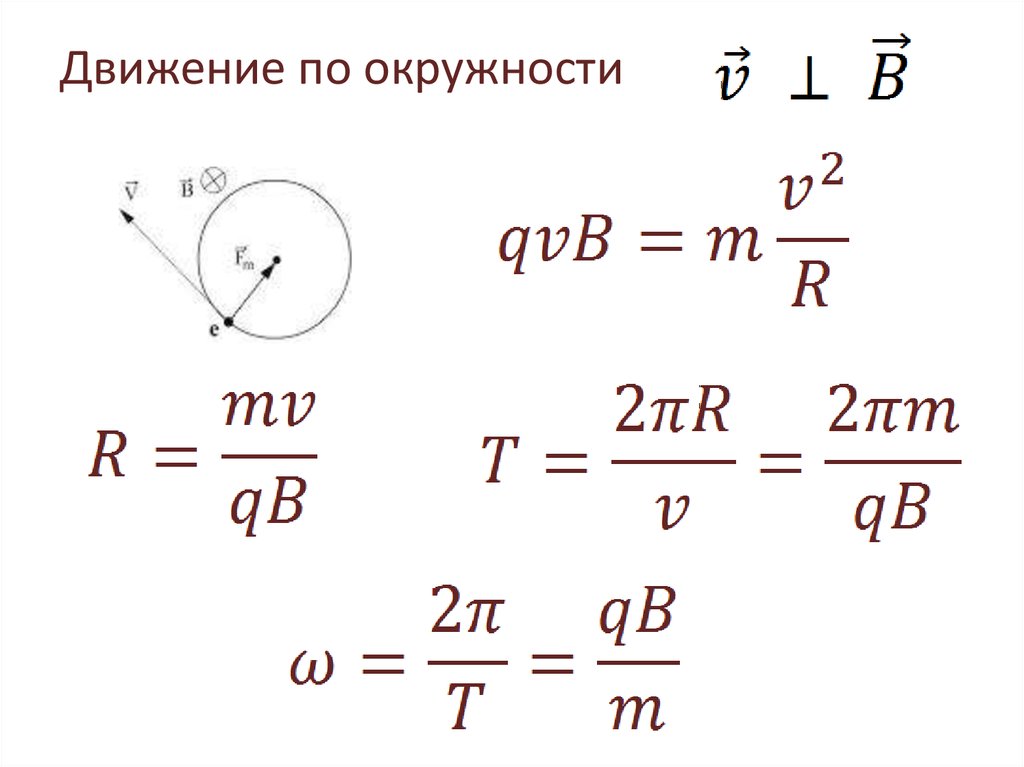 Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_{ц. с.}. Единица измерения — метры на секунду в квадрате (м/с²). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10³ секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10⁶. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Задание EF18273

Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17763

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

• Радиус окружности R₁ = R.
• Радиус окружности R₂ = 4R.
• Центростремительное ускорение: a_ц.с. = a₁ = a₂.

Найти нужно ν₂.

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое.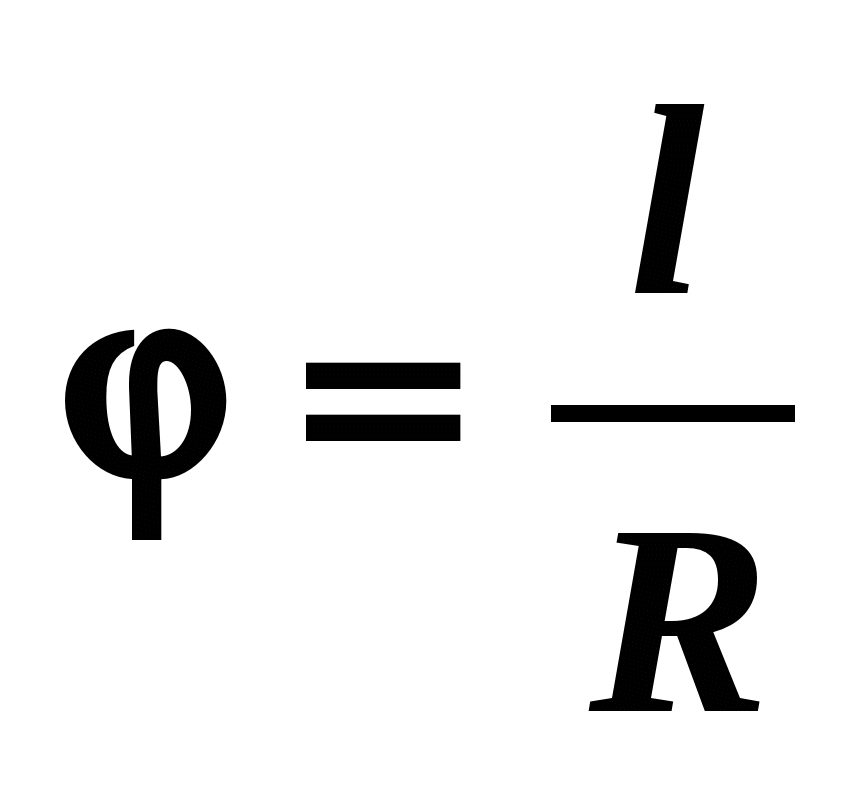 Верный ответ: «б».

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 18.4k

Гармоническое движение

Гармоническое движение

Говорят, что объект, движущийся вдоль оси X, демонстрирует
простое гармоническое движение , если его положение как функция времени изменяется как

x(t) = x ₀ + A cos(ωt + φ).

Объект колеблется вокруг положения равновесия x ₀ . Если мы
выбираем начало нашей системы координат так, что x ₀ = 0, тогда
смещение x от положения равновесия как функция времени определяется выражением

x(t) = A cos(ωt + φ).

А — амплитуда колебаний,
т. е. максимальное смещение объекта из положения равновесия либо в
положительное или отрицательное направление x. Простое гармоническое движение повторяется.
период
T — время, за которое объект
совершить одно колебание и вернуться в исходное положение.
угловая частота ω определяется как ω = 2π/T.
Угловая частота измеряется в радианах в секунду. Обратная сторона
период частота f = 1/T.
частота f = 1/T = ω/2π движения дает число полных колебаний
в единицу времени. Измеряется в герцах (1 Гц = 1/с).

Скорость объекта как функция времени определяется как

v(t) = -ω A sin(ωt + φ),

а ускорение дается

a(t) = -ω ² A cos(ωt + φ) = -ω ² x.

Величина φ называется фазовая постоянная .
Он определяется начальными условиями движения. Если при t = 0
объект имеет максимальное смещение в положительном направлении x, тогда φ = 0, если
он имеет максимальное смещение в отрицательном направлении x, тогда φ = π. Я толстый
t = 0 частица движется через положение равновесия с максимальным
скорость в отрицательном направлении x, тогда φ = π/2. Величина ωt + φ равна
называется фазой .

На рисунке ниже положение и скорость представлены как функция времени.
для колебательного движения с периодом 5 с. Амплитуда и максимальная
скорость имеют условные единицы. Положение и скорость
вне фазы . Скорость равна нулю при максимальном смещении, и
смещение равно нулю на максимальной скорости.

Для простого гармонического движения ускорение a = -ω ² x равно
пропорционально смещению, но в обратном направлении. Простой
гармоническое движение есть ускоренное движение .
Если объект демонстрирует простое гармоническое движение, на него должна действовать сила.
объект. Сила

F = ма = -mω ² х.

Он подчиняется закону Гука , F = -kx, при k = mω ² .

Ссылка:
Простой
гармоническое движение (Youtube)

Сила пружины подчиняется закону Гука. Предположим, что объект
прикреплен к пружине, которая растягивается или сжимается. Тогда пружина давит
сила на объект. Эта сила пропорциональна смещению х тела.
пружинит из положения равновесия и движется в направлении, противоположном
смещение.

Ф = -кх

Предположим, что пружина растянута на расстояние A от положения равновесия, а затем отпущена. Объект
прикрепленный к пружине, ускоряется, возвращаясь к положению равновесия.

a = -(к/м)х

Он набирает скорость по мере продвижения к положению равновесия, потому что его
ускорение направлено в сторону его скорости. Когда он находится в равновесии
положение, ускорение равно нулю, но объект имеет
максимальная скорость. Он выходит за пределы положения равновесия и начинает замедляться.
вниз, потому что ускорение теперь в направлении, противоположном направлению
от его скорости. Пренебрегая трением, он останавливается, когда пружина
сжимается на расстояние А, а затем ускоряется обратно к равновесию
позиция. Он снова промахивается и останавливается в исходном положении, когда
пружина растягивается на расстояние A. Движение повторяется. Объект
колеблется взад и вперед. Он выполняет простое гармоническое движение. Угловой
частота движения

ω = √(к/м),

период

Т = 2π√(м/к),

и частота

f = (1/(2π))√(к/м).

Проблема:

Частица совершает простые гармонические колебания, так что ее
перемещение изменяется согласно выражению x = (5 cm)cos(2t + π/6)
где x в сантиметрах, t в секундах. При t = 0 найти
(а) смещение частицы,
(б)
его скорость и
(c) его ускорение.
(г) Найдите период и амплитуду движения.

Решение:

• Рассуждение:
  Анализ простого гармонического движения.
  x(t) = A cos(ωt + φ). A = амплитуда, ω = угловая частота,
  φ = фазовая постоянная.
  v(t) = -ω A sin(ωt + φ), a(t) = -ω ² A cos(ωt + φ) = -ω ² x.
• Детали расчета:
  (a) Смещение как функция времени: x(t) = Acos(ωt +
  ф). Здесь ω = 2/s, φ = π/6, A = 5 см.
  Перемещение при t = 0 равно x(0) = (5 см)cos(π/6) = 4,33 см.
  (b) Скорость при t = 0 равна v(0) = -ω(5 см)sin(π/6) = -5 см/с.
  (c) Ускорение при t = 0 равно a(0) = -ω ² (5
  см)cos(π/6) = -17,3 см/с ² .
  (d) Период движения T =
  2π/ω = π с, а амплитуда равна 5
  см.

Проблема:

Частица массой 20 г движется в простом гармоническом движении с частотой 3
колебаний в секунду и амплитудой 5 см.
(а) Какое общее расстояние проходит частица за один цикл
его движение?
(b)  Какова его максимальная скорость? Где это происходит?
(c) Найдите максимальное ускорение частицы. Где в движении делает
происходит максимальное ускорение?

Решение:

• Рассуждение:
  Проанализируйте простое гармоническое движение, x(t) = A cos(ωt + φ).
• Детали расчета:
  (a) Общее расстояние d, которое проходит частица за один цикл, равно
  от x = -A до x = +A и обратно к x = -A, поэтому d = 4A = 20 см.
  (b) Максимальная скорость частицы
  
  v _макс.
  = ωA = 2πfA = 2π 15 см/с =
  0,94 м/с.
  Частица имеет максимальную скорость при прохождении через
  положение равновесия.
  (c) Максимальное ускорение частицы равно
  до _макс.
  = ω ² А = (2πf) ² А = 17,8 м/с ² .
  
  Частица имеет максимальное ускорение в точках поворота, где
  имеет максимальное водоизмещение.

Предположим, что масса подвешена к вертикальной пружине с жесткостью k. В
равновесия пружина растянута на расстояние x ₀ = мг/к. Если
масса смещается из положения равновесия вниз, а пружина растягивается
дополнительное расстояние x, то полная сила, действующая на массу, равна mg — k(x ₀
+ x) = -kx, направленный в сторону положения равновесия. Если масса
смещен вверх на расстояние x, то полная сила, действующая на массу, равна mg — k(x ₀
— х) = kx, направленный к положению равновесия. Масса будет
выполнять простые гармонические движения. Угловая частота ω = SQRT(k/m) такая же
для массы, колеблющейся на пружине в вертикальном или горизонтальном положении.
Но равновесная длина пружины, вокруг которой она колеблется, различна для
вертикальное положение и горизонтальное положение.

Предположим, что объект, прикрепленный к пружине, совершает простое гармоническое движение. Позволять
один конец пружины прикрепите к стене и дайте предмету двигаться горизонтально
на столе без трения.

Какова полная энергия объекта?

Кинетическая энергия объекта

K = ½mv ² = ½mω ² A ² sin ² (ωt
+ ф).

Его потенциальная энергия является упругой потенциальной энергией. Упругий потенциал
энергия, накопленная в пружине, смещенной на расстояние x от положения равновесия
U = ½kx ² . Таким образом, потенциальная энергия объекта равна

.

U = ½kx ² = ½mω ² x ² =
½mω ² A ² cos ² (ωt + φ).

Полная механическая энергия объекта

E = K + U = ½mω ² A ² (sin ² (ωt
+ φ) + cos ² (ωt + φ)) = ½mω ² A ² .

Энергия E в системе пропорциональна квадрат амплитуды .

Е = ½ кА ² .

Это постоянно меняющаяся смесь кинетической и потенциальной энергии.

Для любого объекта, совершающего простое гармоническое движение с угловой частотой ω,
восстанавливающая сила F = -mω ² x подчиняется закону Гука и, следовательно, является
консервативная сила . Мы можем определить потенциальную энергию U = ½mω ² x ² ,
а полная энергия объекта определяется выражением E = ½mω ² А ² . Поскольку v _max = ωA,
мы также можем написать E = ½mv _max ² .

Проблема:

Частица, подвешенная на пружине, совершает колебания с угловой частотой 2
рад/с. Пружина подвешена к потолку кабины лифта и висит
неподвижно (относительно автомобиля) по мере снижения автомобиля с постоянной скоростью 1,5
РС. Затем машина внезапно останавливается. Массой пружины пренебречь.
С какой амплитудой колеблется частица?

Решение:

• Рассуждение:
  При движении в лифте с постоянной скоростью общая сила, действующая на
  масса равна нулю. Сила, действующая на пружину, по величине равна силе
  силы тяжести, действующей на массу, пружина имеет равновесную длину
  вертикальная пружина. Когда лифт внезапно останавливается, конец пружины
  крепятся к потолочным упорам. Однако масса имеет импульс, p = mv,
  и поэтому начинает растягивать пружину. Он движется через
  положение равновесия вертикальной пружины с ее максимальной скоростью v _макс.
  = 1,5 м/с.
  Его скорость как функция времени равна v(t) = -ωAsin(ωt + φ).
• Детали расчета:
  Поскольку v _max = ωA и ω = 2/с, амплитуда амплитуды
  колебания А = 0,75 м.

Проблема:

Система масса-пружина совершает колебания с амплитудой 3,5 см. Если сила
постоянная пружины 250 Н/м и масса 0,5 кг, определить
(а) механическая энергия системы,
(b) максимальная скорость массы и
в) максимальное ускорение.

Решение:

• Рассуждение:
  Механическая энергия системы, совершающей простое гармоническое движение, равна E = ½kA ²
  = ½mω ² А ² .
• Детали расчета:
  (а) Имеем m = 0,5 кг, A = 0,035 м, k = 250 Н/м, ω ²
  = к/м
  = 500/с ² , ω = 22,36/с.
  Механическая энергия системы E = ½kA ²
  = 0,153 Дж.
  (б) Максимальная скорость массы равна v _макс.
  = ωA = 0,78 м/с.
  (c) Максимальное ускорение составляет _макс.
  = ω ² А =
  17,5 м/с ² .

кинематика — Угловая скорость или частота при равномерном круговом движении? (для учащихся ВУЗов без исчисления)

$\begingroup$

При равномерном круговом движении мы знаем, что угловая скорость равна:

$$\omega=\frac{2\pi}{T}$$
и ваша мера:

$$[\omega]=\frac{\text{rad}}{\text{s}}$$
то есть оборотов в секунду ( на итальянском языке giri al secondo ).

Теперь частота $\nu$ равна числу циклов в секунду ( на итальянском языке cicli al secondo ),

$$\nu=\frac1T \iff [\nu]=\frac{ 1\, \text{циклы}}{1\, \text s}$$
с единицей измерения $\nu$ равно $1/\text{s}=\text{Hz}$. 9{-1}$.

Мой вопрос:

Не создает ли это путаницу между угловой скоростью и частотой в единицах измерения? Когда в упражнении дается число оборотов в минуту, мы рассматриваем угловую скорость или частоту?

В этом упражнении, например, используется

частота $\nu=f$, а не $\omega$. Но в другом упражнении она берется как $\omega$, а не как частота $\nu=f$. Смотрите изображение,

Верно, что $$\omega=2\pi\nu\equiv 2\pi f$$

но…

есть ли уловка или целесообразность, чтобы определить, является ли это угловой скоростью или частотой?

• кинематика
• частота
• кинематика вращения
• единицы
• единицы si

$\endgroup$

$\begingroup$

В вашей книге используется следующее соотношение:

$$\omega = \frac{d \theta}{dt}$$ 9{-1}$ единиц. Это потому, что радиан является безразмерной единицей в системе СИ, поэтому рад/с эквивалентен 1 доллару/с$. Частота $f$ или $\nu$ выражена в единицах $1/с$, а период $T$ — в секундах. На практике $rad/s$ используется для угловой частоты, а $1/s$ — для нормальной частоты, а не для угловой частоты. Я думаю, что термин rad был опущен при формулировании квантовой механики. Например, $E = hf$, энергия выражается в эВ или Дж, а частота — в Герцах, таким образом, планковская постоянная выражается в $J\cdot s$, а h-bar (приведенная планковская постоянная) выражается в единицах $J\cdot s. /рад$

$\endgroup$

6

$\begingroup$

Это не должно вводить в заблуждение, потому что с величиной связаны некоторые единицы измерения, но обратное не всегда верно, поэтому так думать может быть опасно.

Другими словами, единицы могут дать вам подсказки того, что это такое, но это не единственное, на что вам следует обратить внимание. {-1}$ относится к $\omega$, а $\text{Hz}$ относится к $\nu$.

Это, однако, не абсолютная истина, у каждого автора могут быть свои критерии.

Как я понимаю, если они просто говорят «частота», то следует придерживаться буквального значения и они не смогут вас наказать. Особенно, когда дело доходит до официальных экзаменов и всего такого.

…Если в дальнейшей разработке не появится что-то, что покажет, что на самом деле это была $\omega$, знаете ли, обычно это зависит от логики и контекста…

$\endgroup$

1

$\begingroup$

Окружность радиуса $r$ равна $2\pi r$.

Итак, если круг вращается со скоростью $f$ оборотов в секунду, точка на окружности перемещается на расстояние $2\pi r f$ за одну секунду, поэтому ее скорость равна $2\pi r f$.

Если мы измеряем скорость вращения как $\omega$ радиан в секунду, точка на окружности перемещается на расстояние $r\omega$ за одну секунду.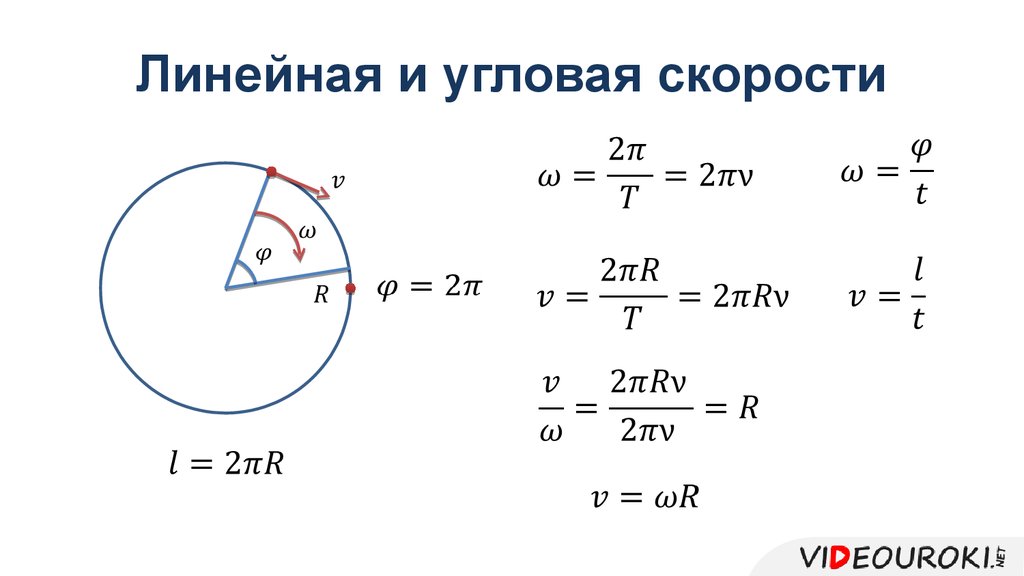

Так как другие формулы для кругового движения также проще при измерении угловой скорости в радианах/сек, хороший способ избежать путаницы состоит в том, чтобы преобразовать другие единицы (например, число оборотов в минуту) в радианы/сек в начале вычислений.

При исчислении во всех формулах используются углы, измеренные в радианах, а не в оборотах или градусах, поэтому лучше сразу использовать радианы.

$\endgroup$

1

$\begingroup$

Думаю, следует также отметить, что
угловая скорость — это то, что известно как вектор , что означает, что он имеет как величину, так и направление. Ваше уравнение для мгновенной угловой скорости действительно должно быть выражено с помощью единичного вектора, так что

$$\vec \omega = \frac{ \Delta \theta}{ \Delta t} \hat u$$

, где единичный вектор $\hat u$ указывает в направлении оси вращения.