Содержание
Рассчитать КБМ по базе РСА онлайн
Аббревиатура КБМ — сокращенное обозначение коэффициента бонус-малус, влияющего на стоимость полиса (повышающий или понижающий в зависимости от аварийности в предыдущие периоды). Максимальная скидка может достигать до 54 % от стоимости ОСАГО.
Рассчитать КБМ
Что представляет собой коэффициент КБМ
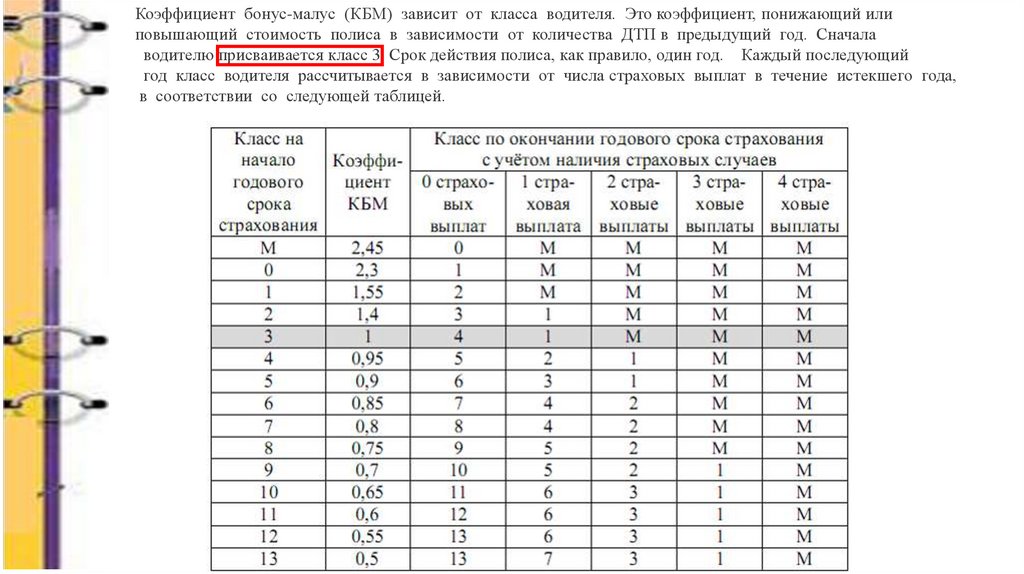
В соответствии с Указанием Банка России от 8 декабря 2021 года N 6007-У «О страховых тарифах по обязательному страхованию гражданской ответственности владельцев транспортных средств» значения коэффициентов КБМ приведены в таблице:
Ниже коэффициенты КБМ, которые будут использоваться при расчёте страховой премии по договорам ОСАГО, которые будут заключаться с 01 апреля 2022г.: по 31 марта 2023г.:
| № п/п | Класс КБМ на период КБМ | Коэффициент КБМ на период КБМ | Коэффициент КБМ | ||||
|---|---|---|---|---|---|---|---|
| отсутствие страховых возмещений за период КБМ | одно страховое возмещение за период КБМ | два страховых возмещения за период КБМ | три страховых возмещения за период КБМ | более трех страховых возмещений за период КБМ | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | М | 3,92 | 0 | М | М | М | М |
| 2 | 0 | 2,94 | 1 | М | М | М | М |
| 3 | 1 | 2,25 | 2 | М | М | М | М |
| 4 | 2 | 1,76 | 3 | 1 | М | М | М |
| 5 | 3 | 1,17 | 4 | 1 | М | М | М |
| 6 | 4 | 1 | 5 | 2 | 1 | М | М |
| 7 | 5 | 0,91 | 6 | 3 | 1 | М | М |
| 8 | 6 | 0,83 | 7 | 4 | 2 | М | М |
| 9 | 7 | 0,78 | 8 | 4 | 2 | М | М |
| 10 | 8 | 0,74 | 9 | 5 | 2 | М | М |
| 11 | 9 | 0,68 | 10 | 5 | 2 | 1 | М |
| 12 | 10 | 0,63 | 11 | 6 | 3 | 1 | М |
| 13 | 11 | 0,57 | 12 | 6 | 3 | 1 | М |
| 14 | 12 | 0,52 | 13 | 6 | 3 | 1 | М |
| 15 | 13 | 0,46 | 13 | 7 | 3 | 1 | М |
Система бонус-малус предполагает применение как понижающих, так и повышающих коэффициентов, если водитель допустил аварию по своей вине и потерпевшим была произведена страховая выплата. На применяемый КБМ по договору ОСАГО влияют все произошедшие ДТП по вине водителя.
На применяемый КБМ по договору ОСАГО влияют все произошедшие ДТП по вине водителя.
При заключении договора ОСАГО значение КБМ по каждому водителю определяется по запросу в автоматизированную информационную систему РСА (АИС ОСАГО).
В соответствии Приложением 4 к Указанию Банка России от 8 декабря 2021 года N 6007-У » О страховых тарифах по обязательному страхованию гражданской ответственности владельцев транспортных средств» с 1 апреля 2022г. для договоров ОСАГО, не предусматривающих ограничение числа лиц, допущенных к управлению транспортным средством, владельцем которого является физическое лицо, страховая премия рассчитывается с применением коэффициента КБМ = 1,17.
Что такое период КБМ и как часто он меняется
В настоящее время КБМ всех водителей меняется один раз в год, а именно 1 апреля и является неизменным в течении года (до 31 марта следующего года).
КБМ рассчитывается по расчетным периодам (период КБМ) в 1 календарный год.
Примеры периодов КБМ:
- С 01.
 04.2020 г. по 31.03.2021 г.;
04.2020 г. по 31.03.2021 г.;
- С 01.04.2021 г. по 31.03.2022 г. и т.д.
КБМ рассчитывается на дату заключения договора ОСАГО (не путать с датой начала срока страхования по договору ОСАГО).
Например, водитель 25.03.2022 г. оформил полис ОСАГО со сроком действия с 05.04.2022 г. по 04.04.2023 г.
В данном случае будет применен расчетный период КБМ с 01.04.2021 г. по 31.03.2022 г. несмотря на то, что договор начинает действовать позже.
Что делать Страхователю, если он не согласен со значением КБМ, полученным из АИС ОСАГО и примененным Страховщиком при заключении договора по конкретному водителю из договора
ВАЖНО! Для дальнейших действий у Страхователя должен быть действующий договор с АО «АльфаСтрахование»
Вам достаточно пройти по ссылке https://www.alfastrah.ru/web-feedback/kbm/ и заполнить соответствующие поля.
ВАЖНО!
Для проверки КБМ необходимы следующие данные:
- ФИО водителя;
- Дата рождения водителя;
- Серия и номер водительского удостоверения водителя;
- Действующий договор с АО «АльфаСтрахование»;
- Серия и номер ранее выданного водительского удостоверения водителя (при наличии).

Значение коэффициентов КБМ до 01 апреля 2022 г. :
| Класс КБМ на период КБМ | Коэффициент КБМ на период КБМ (до 01.04.2022) | Коэффициент КБМ на период КБМ (после 01.04.2022) | Класс КБМ | ||||
|---|---|---|---|---|---|---|---|
| отсутствие страховых возмещений за период КБМ | одно страховое возмещение за период КБМ | два страховых возмещения за период КБМ | три страховых возмещения за период КБМ | более трех страховых возмещений за период КБМ | |||
| М | 2,45 | 3,92 | 0 | М | М | М | М |
| 0 | 2,3 | 2,94 | 1 | М | М | М | М |
| 1 | 1,55 | 2,25 | 2 | М | М | М | М |
| 2 | 1,4 | 1,76 | 3 | 1 | М | М | М |
| 3 | 1 | 1,17 | 4 | 1 | М | М | М |
| 4 | 0,95 | 1 | 5 | 2 | 1 | М | М |
| 5 | 0,9 | 0,91 | 6 | 3 | 1 | М | М |
| 6 | 0,85 | 0,83 | 7 | 4 | 2 | М | М |
| 7 | 0,8 | 0,78 | 8 | 4 | 2 | М | М |
| 8 | 0,75 | 0,74 | 9 | 5 | 2 | М | М |
| 9 | 0,7 | 0,68 | 10 | 5 | 2 | 1 | М |
| 10 | 0,65 | 0,63 | 11 | 6 | 3 | 1 | М |
| 11 | 0,6 | 0,57 | 12 | 6 | 3 | 1 | М |
| 12 | 0,55 | 0,52 | 13 | 6 | 3 | 1 | М |
| 13 | 0,5 | 0,46 | 13 | 7 | 3 | 1 | М |
Рассчитать КБМ
Почему «АльфаСтрахование»
страховых продуктов
для частных лиц
и компаний
региональных
представительств
Исключительно высокий
уровень надежности*
лет на рынке
страховых услуг
ОНЛАЙН
оформление
полисов
что это и как проверить по базе, расчет при ОСАГО
Стоимость полиса ОСАГО — обязательного страхования автогражданской ответственности — зависит от страховой истории водителя.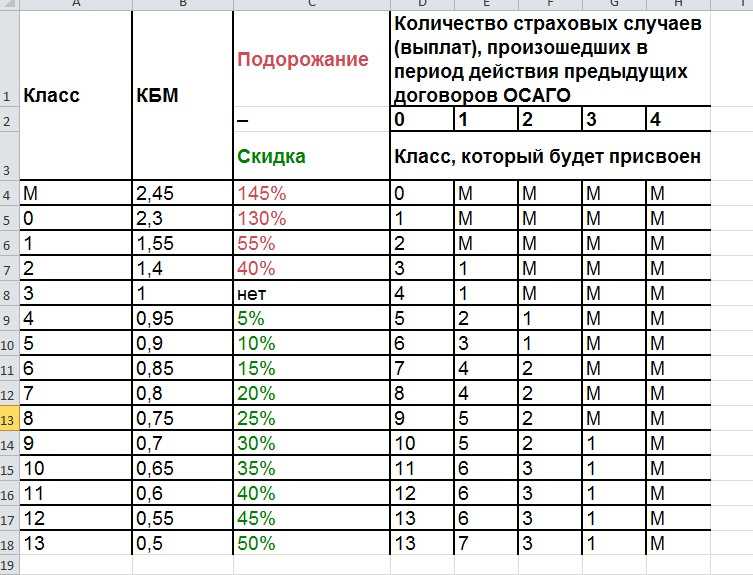 Могут дать скидку за безаварийную езду или, наоборот, надбавку — если были страховые случаи.
Могут дать скидку за безаварийную езду или, наоборот, надбавку — если были страховые случаи.
Георгий Шабашев
страхуется со скидкой
Профиль автора
Разберем, как рассчитывается КБМ и сколько можно сэкономить.
Что такое КБМ
При оформлении страхового полиса ОСАГО стоимость полиса — страховая премия — зависит от базового тарифа, который умножается на различные коэффициенты — региональный, стаж водителя, мощность, период использования и другие. Так получается итоговая стоимость полиса.
КБМ — один из таких коэффициентов — это скидка за то, что у застрахованного водителя не было ДТП по его вине. Если ДТП были, то КБМ возрастает и может превратиться в надбавку — тогда полис будет дороже. То есть чем аккуратнее водите, тем дешевле страховка.
/guide/dogovor-strahovaniya/
Как оформить договор страхования
Законодательство. Размер базовых тарифов для разных категорий автомобилей и коэффициенты, в том числе КБМ, регулирует Центральный банк РФ.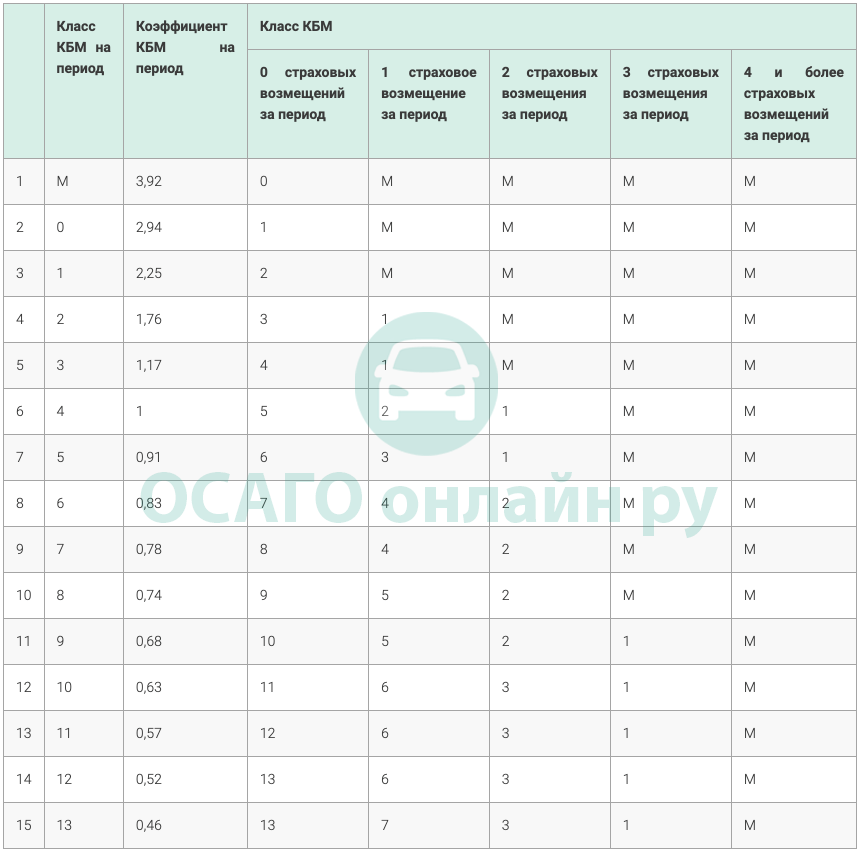
С 2022 года базовый тариф для водителей легковых автомобилей рассчитывается индивидуально, в диапазоне от 2224 до 5980 Р. С 1 апреля минимальный КБМ для аккуратных водителей уменьшили с 0,5 до 0,46, а максимальный увеличили с 2,45 до 3,92
Указание ЦБ о страховых тарифах по ОСАГОPDF, 3,67 МБ
ФЗ «Об обязательном страховании гражданской ответственности владельцев транспортных средств»
Где указывается в полисе. В оформленном полисе ОСАГО все коэффициенты, на основании которых была рассчитана страховая премия, указываются в пункте 7 — «Расчет размера страховой премии». КБМ каждого водителя, допущенного к управлению, указан в таблице из пункта 3.
Коэффициент бонус-малус (КБМ) указывается напротив имени каждого допущенного к управлению лица — индивидуальный КБМ водителя. В нижней части полиса в таблице расчета страховой премии в графе «КБМ» — КБМ, влияющий на стоимость полиса
Виды КБМ
При заключении договора ОСАГО страхователь может указать список водителей, допущенных к управлению, или оформить полис на неограниченное количество лиц — любой водитель, который сядет за руль, будет «вписан» в страховой полис. От этого зависит КБМ и стоимость страхового полиса.
От этого зависит КБМ и стоимость страхового полиса.
КБМ водителя (ограниченная страховка). Если страхователь страхует ответственность конкретных водителей, в полис вносят данные по каждому водителю — фамилию, имя, отчество, номер водительского удостоверения. КБМ считают у каждого водителя по его персональной истории страхования.
Что делать? 11.04.17
Стоит ли регистрировать автомобиль в соседней области ради экономии?
Когда рассчитывают стоимость полиса, берут максимальный КБМ, поэтому стоимость страховки зависит от водителя с наибольшим — «худшим» — коэффициентом.
Например, вы в очередной раз оформляете ОСАГО на себя и хотите вписать второго водителя. Если ваш КБМ равен 0,52, а КБМ второго водителя — 1,76, то скидки при оформлении вы не получите. Стоимость полиса будет рассчитана из расчета наибольшего КБМ, то есть 1,76. Если исключить второго водителя из списка допущенных водителей, полис станет дешевле в три с лишним раза.
КБМ собственника (неограниченная страховка). Если страховать автомобиль без ограничения списка допущенных водителей, КБМ водителей не будет учитываться.
Например, если страхователь из предыдущего примера — владелец автомобиля, он может оформить договор страхования без ограничения перечня водителей. Тогда появится коэффициент за «неограниченность» списка водителей — КО. С 1 апреля 2022 года он равен 2,32. Поэтому неограниченная страховка выгодна, если у одного из водителей КБМ больше 2,32.
Например, если страхователь из предыдущего примера — владелец автомобиля, он может оформить договор страхования без ограничения перечня водителей. Тогда при расчете стоимости полиса будет взят КБМ 1, но в этом случае появится коэффициент за «неограниченность» списка водителей — КО. В этом случае он равен 1,87, то есть надбавка 87%. Поэтому неограниченная страховка выгодна, если у одного из водителей КБМ больше 2.
Когда применяется КБМ
КБМ водителя рассчитывают на основании данных ОСАГО за предыдущий страховой период. В зависимости от того, были или нет страховые выплаты, КБМ водителя увеличивается или уменьшается и используется для вычисления стоимости нового полиса.
В зависимости от того, были или нет страховые выплаты, КБМ водителя увеличивается или уменьшается и используется для вычисления стоимости нового полиса.
Если водитель страхуется впервые, его КБМ принимается равным 1,17.
КБМ может «обнулиться» — стать равным значению КБМ нового водителя. Такое может произойти при смене фамилии или водительского удостоверения. Когда водитель получает новое удостоверение, он должен сообщить о замене в страховую компанию и получить новый страховой полис с актуальными данными. Если этого не сделать, при наступлении страхового случая страховая компания может отказать в выплате: формально в полисе указан другой водитель с другим номером прав.
Еще так происходит, если страховщик ошибся или несвоевременно внес данные в единую базу. Чтобы избежать таких ситуаций, лучше следить за своим КБМ через онлайн-сервис.
Раньше КБМ мог «обнулиться» еще по одной причине — если водитель не заключал договоры страхования за предыдущий период. Так, те, кто часто попадали в аварии, по истечении одного года могли вновь получить полис ОСАГО по номинальной стоимости.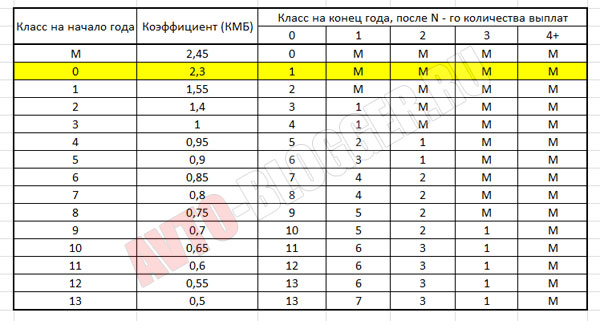 Сейчас полученный КБМ можно снизить только безаварийным вождением.
Сейчас полученный КБМ можно снизить только безаварийным вождением.
Перед вычислением КБМ выберите параметры страхового полиса Укажите данные водителя: фамилию, имя, отчество, его дату рождения, серию и номер водительского удостоверения КБМ водителя по результатам проверки будет указан в нижней части страницы
Откуда берут данные для расчета
Когда водитель получает свои первые права, страховая компания присваивает ему КБМ, равный 1,17. Если бы водитель всегда страховался в той же компании, страховая могла бы сама определить КБМ водителя через год. Но водители могут менять страховую компанию или страховать разные автомобили у разных страховщиков. На этот случай ввели единую базу.
База КБМ АИС РСА — часть автоматизированной информационной системы Российского союза автостраховщиков — хранит историю страхования по каждому водителю. В эту базу попадают данные об оформлении новых страховых полисов ОСАГО из всех страховых компаний, информация о страховых случаях и выплатах, в которых указанный водитель был признан виновником. Эти данные учитывают при расчете КБМ водителя. Данные в АИС РСА могут вносить только страховые компании.
Эти данные учитывают при расчете КБМ водителя. Данные в АИС РСА могут вносить только страховые компании.
Справка о безаварийной езде — документ, который использовался ранее, когда водитель менял одну страховую компанию на другую. С появлением АИС РСА страховые компании стали запрашивать эти данные самостоятельно.
До появления единой базы эта справка требовалась в новой страховой компании, чтобы верно рассчитали КБМ. Справку о безаварийной езде или о наличии страховых выплат выдавала прежняя страховая компания.
Если водитель предоставил недостоверные сведения при отсутствии технической возможности получения их из базы. Сейчас сложно представить, что страховая выпишет полис без проверки КБМ водителя или собственника по базе РСА. Чтобы оформить полис, страховая компания должна сделать запрос в электронную базу РСА.
Изумительная история 28.05.20
Мужчина попал в аварию без ОСАГО, но страховая все равно за него заплатила
Но если водитель по какой-то причине предоставит на оформлении поддельное водительское удостоверение или другие данные, по которым нет истории страхования в базе, ему назначат КБМ в размере 1,17 — как новому водителю.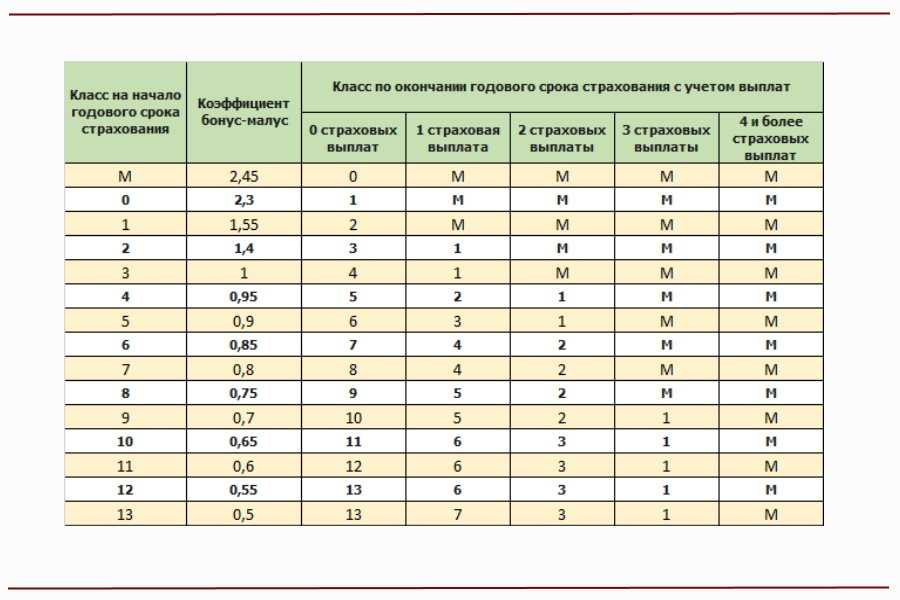 Но при первом же ДТП при проверке в ГИБДД номера прав страховку признают недействительной, а случай — нестраховым, потому что страхователь предоставил страховщику ложные данные.
Но при первом же ДТП при проверке в ГИБДД номера прав страховку признают недействительной, а случай — нестраховым, потому что страхователь предоставил страховщику ложные данные.
Как считается КБМ при оформлении ОСАГО
Раз в год 1 апреля КБМ водителя пересчитывается. Новый КБМ зависит от количества страховых случаев за прошлый год. Но есть и исключения: из-за перехода в 2019 году к новой системе расчета для некоторых пограничных случаев КБМ рассчитывается сложнее. Например, если вы целый год не страховались, то КБМ будет рассчитан с учетом истории страхования, а не обнулится.
Если вы уже страховались после 1 апреля 2019 года, значит, КБМ по новой формуле уже рассчитан. При оформлении страховки на следующий год КБМ можно узнать по таблице.
/guide/polis-osago/
Как устроено ОСАГО
Таблица КБМ показывает, как изменяется КБМ. Для вычисления КБМ водителя нужно знать две вещи:
- КБМ водителя на предыдущий страховой период.
 Каждому значению КБМ соответствует класс, который обозначается буквой или цифрой. М — максимальный класс, КБМ равен 3,92 с 1 апреля 2022 года. 0 — следующий по величине класс, КБМ равен 2,94 с 1 апреля 2022 года. 1 — еще на ступень ниже, КБМ равен 2,25 с 1 апреля 2022 года, и так далее до 13-го класса, КБМ для которого с 1 апреля 2022 года равен 0,46.
Каждому значению КБМ соответствует класс, который обозначается буквой или цифрой. М — максимальный класс, КБМ равен 3,92 с 1 апреля 2022 года. 0 — следующий по величине класс, КБМ равен 2,94 с 1 апреля 2022 года. 1 — еще на ступень ниже, КБМ равен 2,25 с 1 апреля 2022 года, и так далее до 13-го класса, КБМ для которого с 1 апреля 2022 года равен 0,46.
- Количество страховых случаев по вине этого водителя.
Класс КБМ водителя на следующий страховой период находится на пересечении КБМ на начало предыдущего периода и количества страховых случаев.
Таблица расчета коэффициента скидки (КБМ)
| Класс КБМ | Значение КБМ до 1 апреля 2022 | Значение КБМ с 1 апреля 2022 | 0 страховых случаев в течение предыдущего года | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| М | 2,45 | 3,92 | 0 | M | M | M | M |
| 0 | 2,3 | 2,94 | 1 | M | M | M | M |
| 1 | 1,55 | 2,25 | 2 | M | M | M | M |
| 2 | 1,4 | 1,76 | 3 | 1 | M | M | M |
| 3 | 1 | 1,17 | 4 | 1 | M | M | M |
| 4 | 0,95 | 1 | 5 | 2 | 1 | M | M |
| 5 | 0,9 | 0,91 | 6 | 3 | 1 | M | M |
| 6 | 0,85 | 0,83 | 7 | 4 | 2 | M | M |
| 7 | 0,8 | 0,78 | 8 | 4 | 2 | M | M |
| 8 | 0,75 | 0,74 | 9 | 5 | 2 | M | M |
| 9 | 0,7 | 0,68 | 10 | 5 | 2 | 1 | M |
| 10 | 0,65 | 0,63 | 11 | 6 | 3 | 1 | M |
| 11 | 0,6 | 0,57 | 12 | 6 | 3 | 1 | M |
| 12 | 0,55 | 0,52 | 13 | 6 | 3 | 1 | M |
| 13 | 0,5 | 0,46 | 13 | 7 | 3 | 1 | M |
Класс КБМ — М
Значение КБМ до 1 апреля 2022 года
2,45
Значение КБМ с 1 апреля 2022 года
3,92
0 страховых случаев в течение предыдущего года
1 страховой случай в течение предыдущего года
M
2 страховых случая в течение предыдущего года
M
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 0
Значение КБМ до 1 апреля 2022 года
2,3
Значение КБМ с 1 апреля 2022 года
2,94
0 страховых случаев в течение предыдущего года
1
1 страховой случай в течение предыдущего года
M
2 страховых случая в течение предыдущего года
M
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 1
Значение КБМ до 1 апреля 2022 года
1,55
Значение КБМ с 1 апреля 2022 года
2,25
0 страховых случаев в течение предыдущего года
2
1 страховой случай в течение предыдущего года
M
2 страховых случая в течение предыдущего года
M
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 2
Значение КБМ до 1 апреля 2022 года
1,4
Значение КБМ с 1 апреля 2022 года
1,76
0 страховых случаев в течение предыдущего года
3
1 страховой случай в течение предыдущего года
1
2 страховых случая в течение предыдущего года
M
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 3
Значение КБМ до 1 апреля 2022 года
1
Значение КБМ с 1 апреля 2022 года
1,17
0 страховых случаев в течение предыдущего года
4
1 страховой случай в течение предыдущего года
1
2 страховых случая в течение предыдущего года
M
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 4
Значение КБМ до 1 апреля 2022 года
0,95
Значение КБМ с 1 апреля 2022 года
1
0 страховых случаев в течение предыдущего года
5
1 страховой случай в течение предыдущего года
2
2 страховых случая в течение предыдущего года
1
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 5
Значение КБМ до 1 апреля 2022 года
0,9
Значение КБМ с 1 апреля 2022 года
0,91
0 страховых случаев в течение предыдущего года
6
1 страховой случай в течение предыдущего года
3
2 страховых случая в течение предыдущего года
1
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 6
Значение КБМ до 1 апреля 2022 года
0,85
Значение КБМ с 1 апреля 2022 года
0,83
0 страховых случаев в течение предыдущего года
7
1 страховой случай в течение предыдущего года
4
2 страховых случая в течение предыдущего года
2
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 7
Значение КБМ до 1 апреля 2022 года
0,8
Значение КБМ с 1 апреля 2022 года
0,78
0 страховых случаев в течение предыдущего года
8
1 страховой случай в течение предыдущего года
4
2 страховых случая в течение предыдущего года
2
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 8
Значение КБМ до 1 апреля 2022 года
0,75
Значение КБМ с 1 апреля 2022 года
0,74
0 страховых случаев в течение предыдущего года
9
1 страховой случай в течение предыдущего года
5
2 страховых случая в течение предыдущего года
2
3 страховых случая в течение предыдущего года
M
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 9
Значение КБМ до 1 апреля 2022 года
0,7
Значение КБМ с 1 апреля 2022 года
0,68
0 страховых случаев в течение предыдущего года
10
1 страховой случай в течение предыдущего года
5
2 страховых случая в течение предыдущего года
2
3 страховых случая в течение предыдущего года
1
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 10
Значение КБМ до 1 апреля 2022 года
0,65
Значение КБМ с 1 апреля 2022 года
0,63
0 страховых случаев в течение предыдущего года
11
1 страховой случай в течение предыдущего года
6
2 страховых случая в течение предыдущего года
3
3 страховых случая в течение предыдущего года
1
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 11
Значение КБМ до 1 апреля 2022 года
0,6
Значение КБМ с 1 апреля 2022 года
0,57
0 страховых случаев в течение предыдущего года
12
1 страховой случай в течение предыдущего года
6
2 страховых случая в течение предыдущего года
3
3 страховых случая в течение предыдущего года
1
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 12
Значение КБМ до 1 апреля 2022 года
0,55
Значение КБМ с 1 апреля 2022 года
0,52
0 страховых случаев в течение предыдущего года
13
1 страховой случай в течение предыдущего года
6
2 страховых случая в течение предыдущего года
3
3 страховых случая в течение предыдущего года
1
4 страховых случая в течение предыдущего года М
M
Класс КБМ — 13
Значение КБМ до 1 апреля 2022 года
0,5
Значение КБМ с 1 апреля 2022 года
0,46
0 страховых случаев в течение предыдущего года
13
1 страховой случай в течение предыдущего года
7
2 страховых случая в течение предыдущего года
3
3 страховых случая в течение предыдущего года
1
4 страховых случая в течение предыдущего года М
M
С 1 апреля 2022 года выросли коэффициенты у неаккуратных и начинающих водителей и снизились у аккуратных. Если до этой даты у водителя был максимальный КБМ 2,45 и хоть одна авария в течение предыдущего года, то его КБМ становится 3,92 — на 60% больше, чем было. Если водитель с КБМ 2,45 не попадал в аварии, то с 1 апреля его КБМ все равно вырастает — с 2,45 до 2,94. Водитель-новичок получит КБМ 1,17. Водитель с минимальным КБМ 0,5, не попадавший в аварии по своей вине, с 1 апреля будет платить еще меньше — 0,46.
Если до этой даты у водителя был максимальный КБМ 2,45 и хоть одна авария в течение предыдущего года, то его КБМ становится 3,92 — на 60% больше, чем было. Если водитель с КБМ 2,45 не попадал в аварии, то с 1 апреля его КБМ все равно вырастает — с 2,45 до 2,94. Водитель-новичок получит КБМ 1,17. Водитель с минимальным КБМ 0,5, не попадавший в аварии по своей вине, с 1 апреля будет платить еще меньше — 0,46.
п. 2 приложения 2 указания ЦБ РФ № 6007-У от 08.12.2021PDF, 3,6 МБ
С 2023 года, если водитель не был виновником ни в одной аварии в течение прошедшего периода, каждый год его скидка будет увеличиваться, а КБМ — уменьшаться.
Максимальный коэффициент бонус-малус с 1 апреля 2022 года равен 3,92. Это соответствует надбавке 235% относительно стандартного КБМ начинающего водителя. Такая надбавка присваивается, когда по вине застрахованного водителя случается много аварий. Например, такую надбавку получит любой водитель, ставший виновником четырех ДТП за год.
Как определяется количество выплат. Чем чаще водитель становился виновником в ДТП, тем больше выплат производила страховая компания.
Изумительная история 24.08.18
Водитель купил ОСАГО, но его все равно заставили платить за ущерб
Например, если водитель за год участвовал в двух ДТП, но только в одном был признан виновным, то в этом периоде будет одна страховая выплата, которая повлияет на КБМ.
Как определяется последний закончившийся договор. Сейчас КБМ для всех водителей вычисляется один раз в год 1 апреля по итогам прошлого периода — с 1 апреля предыдущего года по 31 марта текущего.
Пример расчета. Если водитель не попадает в аварии с момента выдачи прав, через три года страхования его КБМ будет 0,91, то есть при оформлении очередного полиса ОСАГО он получит скидку около 22%.
Если водитель с КБМ, равным 1 за расчетный год, будет признан виновником в одном ДТП, на следующий страховой период его КБМ будет 1,76, то есть страховой полис обойдется на 76% дороже.
Если водитель ранее не был вписан в полис ОСАГО, то его КБМ считается равным 1,17. Если водитель не был вписан в полис, но в АИС РСА есть информация о нем, КБМ будет рассчитан по имеющимся в единой базе данным.
Если в ОСАГО вписано несколько водителей, вычисляется КБМ каждого водителя и при определении стоимости полиса берется максимальный КБМ самого «аварийного» водителя.
/give-me-insurance/
Как получить компенсацию за травму в аварии
КБМ при досрочном расторжении договора и заключении нового договора будет равен тому значению, которое было у водителя на начало расчетного периода — на 1 апреля.
Что делать, если слетел КБМ
Если КБМ стал равным 1,17, хотя водитель ранее имел скидку и по его вине не было ДТП, нужно написать заявление в страховую компанию с просьбой проверить установленный КБМ и внести изменения в АИС РСА при необходимости.
В заявлении укажите ваши данные, по которым был рассчитан КБМ — серию и номер актуального и (при наличии) предыдущего водительского удостоверения, серию, номер и дату заключения последнего договора страхования, — и в произвольной форме причину, которая, по вашему мнению, повлияла на некорректный расчет КБМ.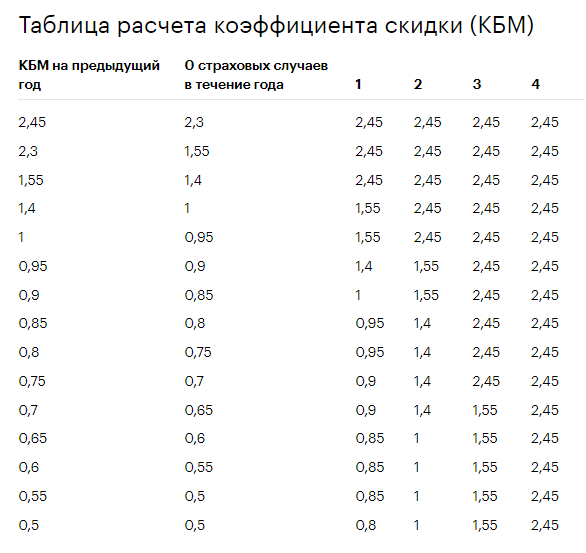 Такая упрощенная процедура исправления в полисе ОСАГО коэффициента бонус-малус называется «КБМ+».
Такая упрощенная процедура исправления в полисе ОСАГО коэффициента бонус-малус называется «КБМ+».
Шаблон заявления в СК
Можно написать заявление в свободной форме или взять наш шаблон
Если страховая компания не может оперативно проверить КБМ и изменить его, проверку осуществит Российский союз автостраховщиков (РСА) в течение пяти рабочих дней по запросу страховой. По результатам проведенной проверки страховщик внесет корректные сведения в АИС РСА.
Но по результатам рассмотрения обращения КБМ могут не только уменьшить, но и увеличить — тогда за страховку придется доплатить.
Например, владелец оформил на автомобиль ОСАГО без ограничения по числу водителей, а другой водитель на этой машине стал виновником ДТП. Такую аварию «запишут» на владельца несмотря на то, что его не было за рулем в тот момент. Тогда при проверке РСА не уменьшит, а увеличит КБМ владельца автомобиля.
Если страховая компания не реагирует на заявление и в установленные сроки не предоставляет мотивированный ответ, можно подать обращение через интернет-приемную Центрального банка.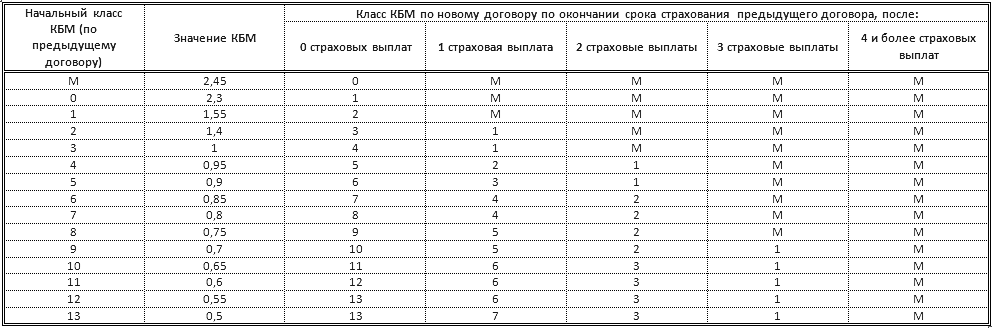 В обращении нужно указать те же данные, что и при обращении в страховую компанию.
В обращении нужно указать те же данные, что и при обращении в страховую компанию.
Откройте страницу «Подать жалобу» в интернет-приемной сайта ЦБ РФ. Найдите блок «Страховые организации» и на вкладке «ОСАГО» выберите пункт «Неверное применение КБМ» Ознакомьтесь со справочной информацией и, если она не поможет, нажмите кнопку «Перейти к оформлению обращения» В форме подачи обращения укажите данные заявителя, информацию об автомобиле и текст обращения
Перерасчет КБМ в течение срока действия полиса
Если после оформления полиса ОСАГО оказалось, что КБМ одного из водителей учтен неверно, необходимо актуализировать информацию в единой базе АИС РСА. Для этого нужно обратиться сначала в свою страховую, а если не поможет — в ЦБ тем способом, который я описал выше.
Когда КБМ обновится, стоимость полиса изменится и появится переплата, которую страховая компания должна вернуть по заявлению.
Анализ премии относительности в системе бонус-малус на основе оптимального линейного метода
На этой странице
АннотацияВведениеБлагодарностиСсылкиАвторское правоСтатьи по теме
автомобильная страховка. Существует много способов, включая байесовскую оценку и обычную линейную оценку, для расчета премии относительности. Здесь нет
Существует много способов, включая байесовскую оценку и обычную линейную оценку, для расчета премии относительности. Здесь нет
сомневаюсь, что байесовская оценка является наиболее точной оценкой; однако это нежелательно для коммерческих целей из-за его довольно нерегулярного рисунка. Эта статья направлена на введение оптимальной линейной оценки премии относительности, которая имеет простую схему и получается при квадратичной функции потерь, так что результат близок к байесовскому методу. Эффективность Лоймаранты такой оптимальной линейной оценки была изучена и сравнена с двумя упомянутыми выше методами.
1. Введение
Бонус-малусная система (BMS) является важной областью исследований в современном актуарии. В страховании BMS представляет собой систему, которая корректирует премию, уплачиваемую держателем полиса, в соответствии с его индивидуальной историей претензий. Бонус обычно представляет собой скидку на премию, которая предоставляется при продлении полиса, если в предыдущем году не было заявлено никаких требований. Малус – это увеличение премии, если в предыдущем году была претензия. Системы бонус-малус очень распространены в страховании транспортных средств. И это интересная тема, как вычислить премию относительности системы бонус-малус.
Малус – это увеличение премии, если в предыдущем году была претензия. Системы бонус-малус очень распространены в страховании транспортных средств. И это интересная тема, как вычислить премию относительности системы бонус-малус.
Рассмотрим систему бонус-малус, содержащую уровни, помеченные от 1 до , и следующий уровень определяется текущим уровнем и количеством требований, зарегистрированных в течение текущего периода. Если количество требований в разные периоды независимо, то траектория данного страхователя будет цепью Маркова. Чтобы справиться с неоднородностью BMS, естественно считать, что количество претензий, вызванных страхователем, предполагается смешанным с распределением Пуассона. Точнее, имеет условную дискретную функцию вероятности следующего вида:
где и представляют собой среднюю частоту и эффект случайного риска соответственно. Случайный эффект представляет собой склонность страхователя к риску, то есть неизвестные характеристики риска, оказывающие существенное влияние на возникновение требований. является функцией распределения . Согласно Норбергу [1], функция массы вероятности, связанная с уровнем для данного страхователя, имеет вид
является функцией распределения . Согласно Норбергу [1], функция массы вероятности, связанная с уровнем для данного страхователя, имеет вид
а байесовская премия относительности при квадратичной функции потерь равна
где – функция распределения и – стационарная вероятность для страхователя с уровнем . Идея байесовского метода состоит в том, чтобы присвоить премию за относительность случайно выбранному страхователю в соответствии с его параметром относительного риска, а близость или относительность измеряется байесовскими методами. Очевидно, что байесовская оценка имеет довольно сложный и нерегулярный характер, и нельзя увидеть, что премия относительности регулярно увеличивается в зависимости от уровня.
Многие авторы обсуждали проблему разработки оптимальной системы бонус-малус. Например, Лемэр и Зи [2] сравнили валидность 30 систем бонус-малус по четырем различным инструментам, таким как относительный стационарный средний уровень премии, коэффициент вариации страховых премий, эффективность системы бонус-малус, и среднее оптимальное удержание.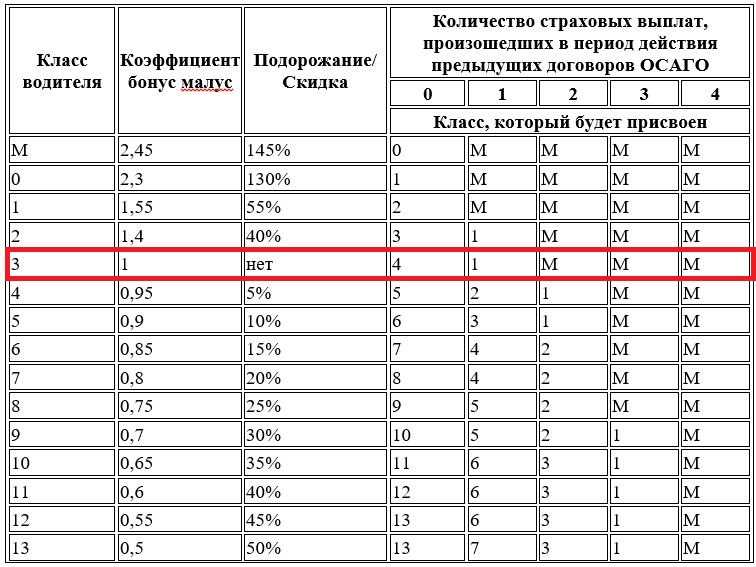 Лемэр [3] предположил, что частота претензий имеет отрицательное биномиальное распределение, и использовал квадратичную функцию потерь для изучения системы бонус-малус. Уолхин и Пэрис [4] обсуждали проблему, в основном, используя конечное распределение смеси Пуассона в качестве частотного распределения требований. Все эти авторы считали частоту претензий наиболее важным фактором и использовали байесовскую оценку. Байесовская оценка не только представляет собой довольно нерегулярную картину, но и может привести к несправедливым результатам без учета серьезности каждого требования. Франгос и Вронтос [5] разработали оптимальную систему бонус-малус, принимая во внимание как частоту, так и тяжесть претензии, а Махмудванд и Хассани [6] разработали систему в обобщенной форме с компонентом частоты и серьезности, основанным как на частоте, так и на серьезности. по априорным и апостериорным критериям классификации. И это имеет смысл для системы, позволяющей как по частоте, так и по серьезности различать разные страховые взносы с одинаковым временем требования, и это справедливо с точки зрения страхователя.
Лемэр [3] предположил, что частота претензий имеет отрицательное биномиальное распределение, и использовал квадратичную функцию потерь для изучения системы бонус-малус. Уолхин и Пэрис [4] обсуждали проблему, в основном, используя конечное распределение смеси Пуассона в качестве частотного распределения требований. Все эти авторы считали частоту претензий наиболее важным фактором и использовали байесовскую оценку. Байесовская оценка не только представляет собой довольно нерегулярную картину, но и может привести к несправедливым результатам без учета серьезности каждого требования. Франгос и Вронтос [5] разработали оптимальную систему бонус-малус, принимая во внимание как частоту, так и тяжесть претензии, а Махмудванд и Хассани [6] разработали систему в обобщенной форме с компонентом частоты и серьезности, основанным как на частоте, так и на серьезности. по априорным и апостериорным критериям классификации. И это имеет смысл для системы, позволяющей как по частоте, так и по серьезности различать разные страховые взносы с одинаковым временем требования, и это справедливо с точки зрения страхователя.
Очевидно, что байесовская оценка имеет довольно сложный и нерегулярный характер. Принимая во внимание недостатки байесовской премии относительности, Гильде и Сундт [7] предложили сглаживать линейным образом; т. е. , , и получили значения параметров и при условии минимизации . Решение можно легко получить следующим образом:
где – ковариация уровня и параметра риска, а – математическое ожидание и дисперсия уровня . С помощью этой оценки, полученной из квадратичной функции потерь и , мы можем легко вычислить надбавку относительности, а линейная модель имеет возрастающее свойство, связанное с уровнем . Но это все равно не гарантирует справедливости со стороны страховщиков, потому что линейная форма налагает ту же самую степень, когда система бонус-малус наказывает или вознаграждает определенного страхователя.
Предполагая, что частота или серьезность распределены по-разному, исследователи последовательно использовали байесовскую или линейную оценки для расчета относительной премии при проектировании или разработке системы бонус-малус. Как бы хорошо ни изображалась неоднородность автострахования со стороны страхователя через распределение частотности или серьезности, поведение со стороны страховщиков представлено не так хорошо. Таким образом, премии относительности, рассчитанные байесовской оценкой, как показывает уравнение (3), или обычной линейной оценкой, как показывает уравнение (4), не учитывают точку зрения страховщиков. С другой стороны, байесовский оценщик имеет довольно сложный шаблон для коммерческого использования и нерегулярный шаблон для механизма оценки качества; то есть связь между премией относительности и уровнем является неявной, хотя и наиболее точной. И обычная линейная оценка, сглаженная из байесовской оценки, не может быть такой же точной, как байесовский метод, и не настолько справедливой из-за той же степени или эффекта, налагаемого на страхователя, когда страховщики наказывают и вознаграждают, хотя его легко вычислить. Учитывая это, в этой статье вводится новая оценка, а именно, оптимальная линейная оценка, которая, как мы ожидаем, будет близка к байесовской оценке для расчета премии относительности.
Как бы хорошо ни изображалась неоднородность автострахования со стороны страхователя через распределение частотности или серьезности, поведение со стороны страховщиков представлено не так хорошо. Таким образом, премии относительности, рассчитанные байесовской оценкой, как показывает уравнение (3), или обычной линейной оценкой, как показывает уравнение (4), не учитывают точку зрения страховщиков. С другой стороны, байесовский оценщик имеет довольно сложный шаблон для коммерческого использования и нерегулярный шаблон для механизма оценки качества; то есть связь между премией относительности и уровнем является неявной, хотя и наиболее точной. И обычная линейная оценка, сглаженная из байесовской оценки, не может быть такой же точной, как байесовский метод, и не настолько справедливой из-за той же степени или эффекта, налагаемого на страхователя, когда страховщики наказывают и вознаграждают, хотя его легко вычислить. Учитывая это, в этой статье вводится новая оценка, а именно, оптимальная линейная оценка, которая, как мы ожидаем, будет близка к байесовской оценке для расчета премии относительности. Оптимальная линейная оценка, полученная из уравнения избыточного капитала с точки зрения страховщиков и с линейной моделью путем сглаживания байесовской оценки по квадратичной функции потерь избыточного капитала, будет не только легко использоваться для вычислений, но и будет намного ближе к Байесовская оценка, чем обычная линейная оценка. И Оптимальная линейная оценка также регулярно увеличивается в зависимости от уровня. Затем мы покажем, чем новый метод работает лучше, чем обычная линейная оценка, представив эффективность Лоймаранты в качестве инструмента для сравнения. Сравнение включает в себя демонстрацию рынка автострахования Гонконга и моделирование системы бонус-малус, учитывающей суммы требований.
Оптимальная линейная оценка, полученная из уравнения избыточного капитала с точки зрения страховщиков и с линейной моделью путем сглаживания байесовской оценки по квадратичной функции потерь избыточного капитала, будет не только легко использоваться для вычислений, но и будет намного ближе к Байесовская оценка, чем обычная линейная оценка. И Оптимальная линейная оценка также регулярно увеличивается в зависимости от уровня. Затем мы покажем, чем новый метод работает лучше, чем обычная линейная оценка, представив эффективность Лоймаранты в качестве инструмента для сравнения. Сравнение включает в себя демонстрацию рынка автострахования Гонконга и моделирование системы бонус-малус, учитывающей суммы требований.
Структура этого документа следующая. В разделе 2 представлен простой метод, а именно, Оптимальная линейная оценка, которую можно использовать для вычисления надбавки относительности в стационарной системе бонус-малус. Сравнение эффективности трех оценщиков, основанное на эффективности Лоймаранты, обсуждается в Разделе 3. В Разделе 3 также представлены некоторые модели и демонстрации, учитывающие серьезность требований каждого страхователя. Затем следуют заключительные замечания.
В Разделе 3 также представлены некоторые модели и демонстрации, учитывающие серьезность требований каждого страхователя. Затем следуют заключительные замечания.
2. Оптимальная линейная теория относительности
Как упоминалось выше, BMS, обсуждаемая в этой статье, имеет уровни, обозначенные от 1 до , где премия относительности связана с уровнем . Задача, рассматриваемая здесь, состоит в том, чтобы определить решение премии оптимальной линейной теории относительности. Чтобы пойти дальше, предположим, что , , представляет количество страхователей на одном уровне в момент времени, является первоначальным капиталом и эталоном премии. Тогда избыточный капитал страховщика в момент времени может быть легко получен как
где обозначает весь премиальный доход и является суммой всех претензий на момент времени. Точно так же мы можем естественным образом получить весь премиальный доход.
связаны с байесовской относительностью и
связанный с оптимальной линейной теорией относительности. Вопрос вопросов состоит в том, чтобы сгладить байесовскую относительность и достичь оптимальной линейной относительности, которая имеет явный линейный паттерн, обозначаемый как
Вопрос вопросов состоит в том, чтобы сгладить байесовскую относительность и достичь оптимальной линейной относительности, которая имеет явный линейный паттерн, обозначаемый как
Мы подходим к этому вопросу с точки зрения избыточного капитала страховщика и добиваемся значений параметров и путем минимизации квадратичной функции потерь .
Для этого мы отдаем приоритет всем премиальным доходам и предполагаем, что первоначальный капитал и сумма всех требований на момент времени должны быть фиксированными, поскольку наша цель — получить ответ , и это предположение подходит здесь.
Предложение 1. Рассмотрим систему бонус-малус, имеющую уровни, помеченные от 1 до , где и , , являющиеся байесовской относительностью и оптимальной линейной относительностью соответственно; тогда минимизация с ограничениями имеет место тогда и только тогда, когда
где и .
Доказательство. Поскольку ориентир премии является постоянным и предполагается фиксированным, очевидно, мы будем иметь
Дифференцируя это уравнение по и , получаем
Упрощая два приведенных выше уравнения, мы имеем
Объедините и решите два уравнения, тогда мы получим предложение, которое нужно доказать.
Из процедуры решения значений параметров и , мы видим, что обсуждаемая здесь Оптимальная линейная теория относительности представляет собой не только линейную модель, минимизирующую функцию риска относительности и параметра риска, но и регулярно увеличивающуюся линейную модель после достаточного обдумывания количество страхователей, связанных с каждым уровнем. Принимая во внимание как уравнение избыточного капитала страховщика, так и распределение количества страхователей на каждом уровне, мы полагаем, что Оптимальная линейная относительность, рассматриваемая в этой статье, будет ближе к байесовской оценке и будет соответствовать лучшему коэффициенту бонус-малус. систему по сравнению с обыкновенной линейной теорией относительности. Кроме того, с помощью явного шаблона можно легко вычислить Оптимальную линейную относительность.
3. Сравнение трех подходов
3.1. Эффективность Loimaranta как инструмент для сравнения
Достоинством хорошей системы бонус-малус является то, что премия, уплачиваемая страхователями, на которых распространяется шкала бонус-малус, увеличивается по мере увеличения ожидаемой частоты требований.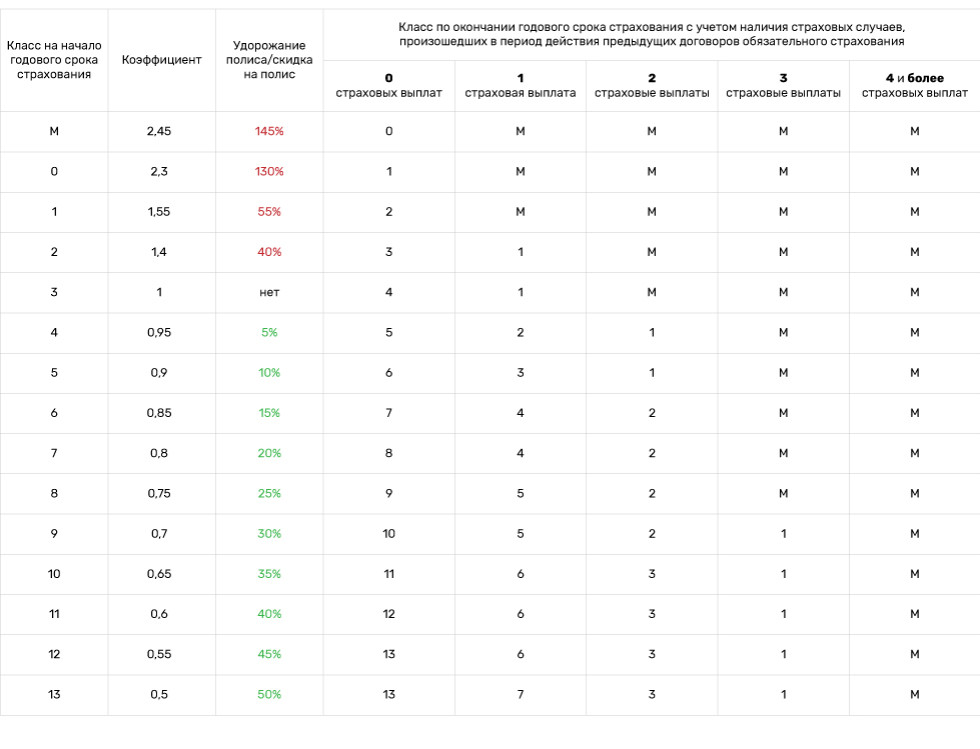 Чем больше повышающая ставка, тем лучше система бонус-малус. А скорость роста связана с концепцией эластичности, которая измеряет реакцию одного фактора на изменение другого. Эффективность Лоймаранта [8] — это просто хороший случай для измерения того, как система бонус-малус реагирует на изменение риска водителя. Средняя относительность, обозначаемая как , имеет следующую формулу после того, как каждый страхователь в конечном итоге стабилизируется около равновесного уровня:
Чем больше повышающая ставка, тем лучше система бонус-малус. А скорость роста связана с концепцией эластичности, которая измеряет реакцию одного фактора на изменение другого. Эффективность Лоймаранта [8] — это просто хороший случай для измерения того, как система бонус-малус реагирует на изменение риска водителя. Средняя относительность, обозначаемая как , имеет следующую формулу после того, как каждый страхователь в конечном итоге стабилизируется около равновесного уровня:
А эффективность Лоймаранты, обозначаемая как , определяется как эластичность средней относительности и имеет следующую формулу:
Эффективность Loimaranta измеряет, как средняя относительность реагирует на изменение средней частоты требований, и в идеале эффективность должна быть близка к 1 для наиболее распространенных значений . Чем больше эффективность, тем лучше система. До сих пор мы давали определение эффективности Лоймаранты для определенной частоты требований. Однако этого недостаточно для глубокого обсуждения, поэтому мы рассчитываем эффективность Loimaranta, которая является функцией годовой ожидаемой частоты претензий, где для явного сравнения. Теперь, когда мы представляем этот полезный инструмент для сравнения, мы сравним три оценочные относительности, а именно байесовскую относительность, обыкновенную линейную относительность и оптимальную линейную относительность, используя некоторые симуляции и демонстрации.
Теперь, когда мы представляем этот полезный инструмент для сравнения, мы сравним три оценочные относительности, а именно байесовскую относительность, обыкновенную линейную относительность и оптимальную линейную относительность, используя некоторые симуляции и демонстрации.
3.2. Сравнение с демонстрацией
Возьмем в качестве примера рынок автострахования Гонконга. Система бонус-малус в Гонконге состоит из 6 уровней, помеченных от 1 до 6, и начальным уровнем является самый высокий уровень 6. Скидка за год без претензий составляет один уровень, а штраф за заявленную претензию — два уровня. Все скидки будут потеряны и перейдут на высший уровень 6 после того, как будет сообщено о более чем одной претензии. Соответствующие правила перехода показаны в таблице 1.
В соответствии с правилами перехода в таблице 1 мы получаем соответствующую матрицу перехода в случае, когда номера заявок имеют смешанное распределение Пуассона:
где , элемент матрицы, обозначает вероятность перехода с уровня на уровень .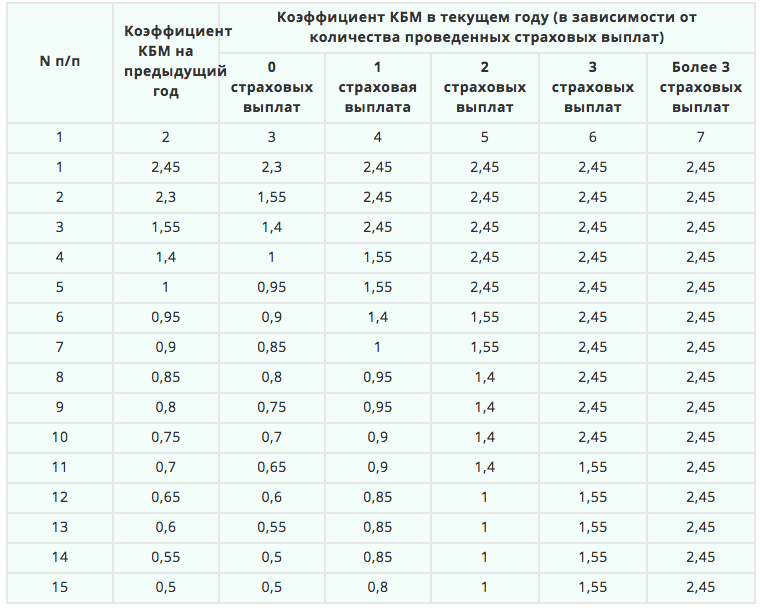 Решение этой стохастической матрицы есть
Решение этой стохастической матрицы есть
где — вектор-столбец из единиц, а — матрица со всеми элементами, равными 1.
Для удобства мы следуем выводу Денуи и др. [9] о том, что средняя частота заявок равна 0,1426, что получается при использовании максимальной вероятности и предположении что эффект случайного риска является гамма-распределенным, то есть . Предположим, что числа страхователей на каждом уровне независимы и распределены по Пуассону со средним значением . С этими предположениями мы получаем соответствующие значения параметров, представленные в таблицах 2 и 3.
Теперь мы готовы сравнить эти три оценочных относительности, используя эффективность Лоймаранты после получения данных, представленных в таблицах 2 и 3. И у нас есть рисунок 1, связанный с другой средней частотой претензий, которая принадлежит интервалу .
Как видно из рисунка 1, эффективность Лоймаранты байесовской теории относительности является самой большой, а эффективность Оптимальной линейной теории относительности лучше, чем обыкновенной линейной теории относительности для всего интервала. Вывод, представленный на рис. 1, подтверждает наши ожидания, что байесовская теория относительности может считаться наиболее точной и, следовательно, наиболее эффективной. Как показано на рис. 1, оптимальная линейная оценка почти достигает эффективности байесовского метода. Кроме того, оптимальная линейная оценка имеет гораздо лучшую эффективность, чем обычная линейная оценка. Теоретически байесовский метод получает результаты, используя априорную информацию о средней частоте требований, поэтому он, безусловно, является наиболее точным. И легко понять, что оптимальная линейная оценка, полученная путем минимизации, имеет лучшую эффективность, чем обычная линейная оценка, полученная путем минимизации, поскольку она намного ближе к байесовской оценке, чем .
Вывод, представленный на рис. 1, подтверждает наши ожидания, что байесовская теория относительности может считаться наиболее точной и, следовательно, наиболее эффективной. Как показано на рис. 1, оптимальная линейная оценка почти достигает эффективности байесовского метода. Кроме того, оптимальная линейная оценка имеет гораздо лучшую эффективность, чем обычная линейная оценка. Теоретически байесовский метод получает результаты, используя априорную информацию о средней частоте требований, поэтому он, безусловно, является наиболее точным. И легко понять, что оптимальная линейная оценка, полученная путем минимизации, имеет лучшую эффективность, чем обычная линейная оценка, полученная путем минимизации, поскольку она намного ближе к байесовской оценке, чем .
3.3. Сравнение с моделированием, учитывающим серьезность претензии
Рассмотрим новую систему бонус-малус, которая имеет 6 уровней, помеченных от 1 до 6, и допускает как количество претензий, так и серьезность претензий. Пусть случайная величина обозначает суммы требований и удовлетворяет требованиям , , и , где и являются определенными заданными суммами требований и удовлетворяют . Пусть случайная величина обозначает номера требований и является функцией распределения . Скидка за год без претензий составляет один уровень. При условии, что заявлена одна претензия, штраф будет двухуровневым, если суммы претензии меньше , и штрафом будет в три уровня, если суммы претензии будут между и . Все скидки будут потеряны, а страхователь перейдет на высший уровень 6 после того, как будет сообщено о двух или более претензиях или сумма претензий превысит . Соответствующие правила перехода показаны в таблице 4.
Пусть случайная величина обозначает суммы требований и удовлетворяет требованиям , , и , где и являются определенными заданными суммами требований и удовлетворяют . Пусть случайная величина обозначает номера требований и является функцией распределения . Скидка за год без претензий составляет один уровень. При условии, что заявлена одна претензия, штраф будет двухуровневым, если суммы претензии меньше , и штрафом будет в три уровня, если суммы претензии будут между и . Все скидки будут потеряны, а страхователь перейдет на высший уровень 6 после того, как будет сообщено о двух или более претензиях или сумма претензий превысит . Соответствующие правила перехода показаны в таблице 4.
В соответствии с правилами перехода в таблице 4 матрица перехода имеет вид Для удобства, но без ограничения общности, мы устанавливаем , , и и , , и . В обоих случаях мы проводим моделирование со всеми упомянутыми выше предположениями; , , элементы независимы и распределены по Пуассону со средним .
Тогда в первом случае, согласно предложению, у нас есть соответствующие значения оценки в таблице 5.
И эффективность Лоймаранты, связанная с этими значениями оценки в таблице 5, показана на рисунке 2.
Показанная на рис. 2 эффективность в некоторой степени превосходит наши ожидания. Эффективность Лоймаранты Оптимальной линейной теории относительности может легко приблизиться к байесовской оценке и, очевидно, работает намного лучше, чем обычная линейная теория относительности во всем заданном интервале .
Для второго случая мы получаем соответствующие значения оценок в таблице 6 согласно предложению.
А эффективность Лоймаранты, связанная с этими значениями оценки в таблице 6, показана на рисунке 3.
На рисунке 3, как и ожидалось, эффективность байесовской теории относительности самая большая, а также эффективность оптимальной линейной теории относительности лучше, чем эффективность обычной линейной теории относительности.
На данный момент мы пришли к выводу, что Оптимальная линейная относительность лучше, чем Обыкновенная линейная относительность, благодаря демонстрации системы бонус-малус в Гонконге и моделированию новой системы бонус-малус, учитывающей тяжесть претензии в соответствии с в рамках эффективности Лоймаранта. Однако единственным недостатком является то, что Оптимальная линейная относительность не так близка к реальному значению, как байесовская относительность; однако он может работать не хуже байесовской оценки. Теоретически и статистически байесовский метод, использующий априорную информацию о средней частоте претензий страхователя, работает лучше, что, безусловно, лучше. полученный из уравнения избыточного капитала и сведенный к минимуму, представляет собой линейную закономерность путем непосредственного сглаживания. полученный путем минимизации, является линейным шаблоном только путем сглаживания параметра случайного риска . Исходя из того, что байесовский метод является наиболее точным, можно понять тот факт, что оптимальная линейная оценка намного ближе к байесовской оценке и работает лучше, чем обычная линейная оценка. И, конечно же, эта статья просто пытается обогатить некоторые методы оценки относительности и ограничивается стандартом эффективности Лоймаранты. Как работает Оптимальная линейная теория относительности, требует дальнейших исследований.
Однако единственным недостатком является то, что Оптимальная линейная относительность не так близка к реальному значению, как байесовская относительность; однако он может работать не хуже байесовской оценки. Теоретически и статистически байесовский метод, использующий априорную информацию о средней частоте претензий страхователя, работает лучше, что, безусловно, лучше. полученный из уравнения избыточного капитала и сведенный к минимуму, представляет собой линейную закономерность путем непосредственного сглаживания. полученный путем минимизации, является линейным шаблоном только путем сглаживания параметра случайного риска . Исходя из того, что байесовский метод является наиболее точным, можно понять тот факт, что оптимальная линейная оценка намного ближе к байесовской оценке и работает лучше, чем обычная линейная оценка. И, конечно же, эта статья просто пытается обогатить некоторые методы оценки относительности и ограничивается стандартом эффективности Лоймаранты. Как работает Оптимальная линейная теория относительности, требует дальнейших исследований. Однако, принимая во внимание все эти условия, Оптимальная линейная теория относительности была бы хорошим методом из-за его относительной точности и простоты.
Однако, принимая во внимание все эти условия, Оптимальная линейная теория относительности была бы хорошим методом из-за его относительной точности и простоты.
Как определить относительность премий — это долгий путь и значительный прогресс, включая построение моделей и поиск способов оценки этих моделей. Из-за нежелательной имплицитности и сложности байесовской оценки, а также некоторых недостатков обычной линейной оценки в этой статье разработан новый метод оценки путем сглаживания байесовской оценки, чтобы он был намного ближе к байесовскому методу. И этот новый метод оценки, который исходил из функции избыточного капитала страховщика, имеет большое эмпирическое значение, поскольку позволяет избежать сложности байесовского метода и более эффективен, чем обычный линейный метод. На практике предложенный Оптимальный линейный метод используется для анализа автомобильного рынка Гонконга и построенной системы бонус-малус с учетом серьезности и оценивается в рамках эффективности Лоймаранты.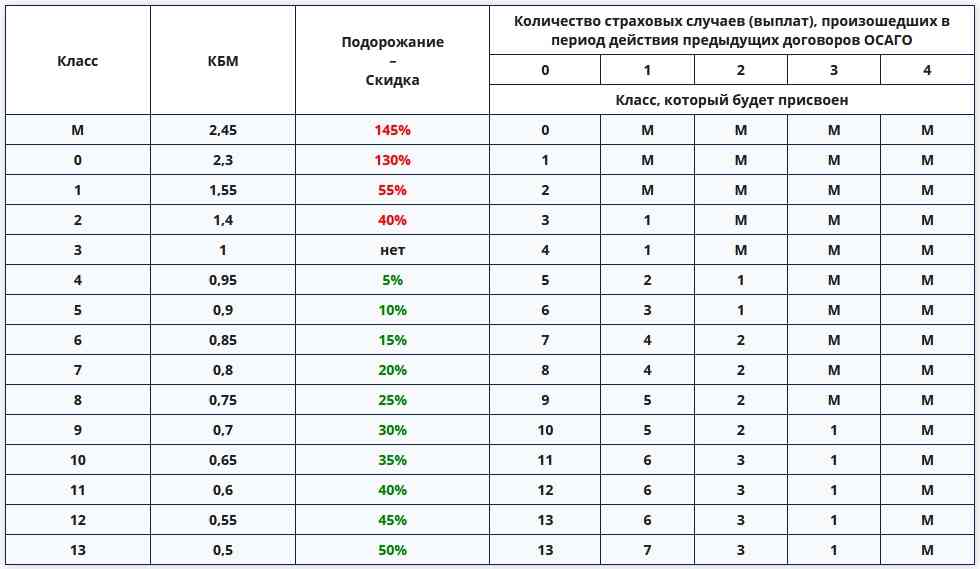 Эффективность Лоймаранта как функция ожидаемой частоты заявок показывает, что предлагаемый оптимальный метод превосходит обычный линейный метод, особенно очевидно, когда он находится в интервале (). Для дальнейших исследований предложенный метод может быть расширен и применен к разным видам рынка автострахования и может быть проверен другими инструментами, а число страхователей на каждом уровне, представленное параметром , может быть тщательно продумано и распространено на другие распределения.
Эффективность Лоймаранта как функция ожидаемой частоты заявок показывает, что предлагаемый оптимальный метод превосходит обычный линейный метод, особенно очевидно, когда он находится в интервале (). Для дальнейших исследований предложенный метод может быть расширен и применен к разным видам рынка автострахования и может быть проверен другими инструментами, а число страхователей на каждом уровне, представленное параметром , может быть тщательно продумано и распространено на другие распределения.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Благодарности
Авторы благодарны редактору и анонимным рецензентам за их полезные замечания и предложения, которые помогли им создать существенно улучшенную версию. Их работа поддерживается Национальным научным фондом Китая (грант № 11171321).
Ссылки
-
Р. Норберг, «Теория доверия к автомобильным бонусным системам», Скандинавский актуарный журнал , вып.
 2, стр. 92–107, 1976.
2, стр. 92–107, 1976.Посмотреть по адресу:
Google Scholar | MathSciNet
-
J. Lemaire и H. Zi, «Сравнительный анализ 30 систем бонус-малус», ASTIN Bulletin , vol. 24, нет. 2, стр. 287–309, 1994.
Посмотреть по адресу:
Сайт издателя | Google Scholar
-
J. Lemaire, Системы бонус-малус в автомобильном страховании , Kluwer Academic, Бостон, Массачусетс, США, 1995.
-
Дж. Ф. Валин и Дж. Пэрис, «Использование смешанного распределения Пуассона в связи с системой бонус-малус», Бюллетень ASTIN , том. 29, стр. 81–99, 1999.
Посмотреть по адресу:
Google Scholar
-
Н. Франгос и С. Вронтос, «Разработка оптимальной системы бонус-малус с компонентом частоты и тяжести на индивидуальной основе в автомобильном страховании», ASTIN Bulletin , vol.
 31, стр. 1–23, 2001.
31, стр. 1–23, 2001.Посмотреть по адресу:
Google Scholar
-
Р. Махмудванд и Х. Хассани, «Обобщенные бонусно-малусные системы с компонентом частоты и серьезности на индивидуальной основе в автомобильном страховании», Astin Bulletin , vol. 39, нет. 1, стр. 307–315, 2009 г.
Посмотреть по адресу:
Сайт издателя | ученый Google | MathSciNet
-
В. Гильде и Б. Сундт, «Системы bomus со шкалами достоверности», Scandinavian Actuarial Journal , стр. 13–22, 199.9.
Посмотреть по адресу:
Google Scholar
-
К. Лоймаранта, «Некоторые асимптотические свойства бонусных систем», ASTIN Bulletin , vol. 6, pp. 223–245, 1972.
Просмотр по адресу:
Google Scholar
-
M.
 Denuit, X. Marechal, S. Pitrebois, and J. F. Walhin, Acturial Modilling of Claimability Counts: Risk Classification, Trustity и Bomus-Malus Systems , Wiley, 2007.
Denuit, X. Marechal, S. Pitrebois, and J. F. Walhin, Acturial Modilling of Claimability Counts: Risk Classification, Trustity и Bomus-Malus Systems , Wiley, 2007.
Copyright
Copyright © 2014 Yu Chen and Long Li. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Премия при расчете: наш онлайн-симулятор
Премия при расчете: наш онлайн-симулятор
Премия за штраф оказывает положительное или отрицательное влияние на сумму вашего страхового взноса в зависимости от вашего опыта вождения. Тем не менее, сложно рассчитать свой бонус-малус. Поэтому наш инструмент здесь, чтобы помочь вам!
Мы также объясним, как рассчитывается ваш премиальный малус и как он влияет на ваш страховой взнос.
Резюме
Как рассчитывается бонус-малус?
Как рассчитать автоштраф?
В каких случаях мой бонус-малус может быть увеличен?
Как узнать бонус автострахования?
Какой дополнительный штраф для молодого водителя?
Смена страховщика или автомобиля: как рассчитать бонусный минус?
Как рассчитывается ваш бонус-малус?
Система бонусов/штрафов позволяет адаптировать сумму страхового взноса к вашему вождению.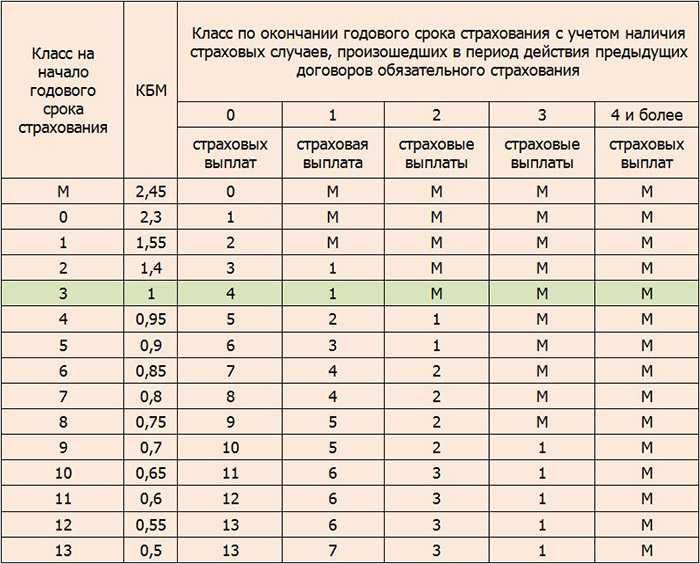 Проще говоря, если вы хороший водитель, вы получите бонус, который уменьшит сумму вашего бонуса. И наоборот, если вы несете ответственность за несчастные случаи, вы будете иметь штраф, который увеличит сумму вашей премии.
Проще говоря, если вы хороший водитель, вы получите бонус, который уменьшит сумму вашего бонуса. И наоборот, если вы несете ответственность за несчастные случаи, вы будете иметь штраф, который увеличит сумму вашей премии.
Эта премия/штраф, также называемая повышением коэффициента уменьшения (CRM), таким образом, позволяет оценить риск, который вы представляете, чтобы адаптировать стоимость вашего автострахования.
Автострахование CRM: как это работает?
CRM (увеличение понижающего коэффициента), также называемое бонусом/малусом, зависит от вашей истории вождения. В зависимости от этой истории ваш эталонный взнос будет пересмотрен в сторону увеличения или уменьшения:
у вас есть бонус, если вы не попали в аварию, поэтому ваш взнос будет уменьшен;
у вас есть штраф, если вы полностью или частично несете ответственность за аварию, поэтому ваш взнос будет увеличен.
При расчете вашей премии/штрафа учитываются только несчастные случаи с долей ответственности. Таким образом, не учитываются: разбитие стекол, аварии на парковке или любые другие аварии без вины.
Таким образом, не учитываются: разбитие стекол, аварии на парковке или любые другие аварии без вины.
Как обновляется мой бонус/штраф?
Ваш CRM рассчитывается за 12-месячный период с двухмесячным отставанием от даты годовщины вашего автоконтракта. Например, если срок действия вашего договора 1 мая, ваш CRM будет рассчитываться за период с 1 марта 2019 года.до 1 марта 2020 г. Таким образом, ваш бонус/штраф автоматически обновляется ежегодно на основе вашей истории несчастных случаев.
По умолчанию, когда вы оформляете свою первую автомобильную страховку, ваш бонус/штраф автоматически устанавливается равным 1.
Таблица бонусных штрафов: сводка правил расчета
Бонус/штраф меняется в зависимости от причиненных вами аварий. Вы всегда начинаете свою жизнь молодым водителем с CRM равным 1. Далее, в зависимости от вашего штрафа или бонуса, этот коэффициент может увеличиваться или уменьшаться.
Вот правила расчета:
вы не стали причиной ответственного несчастного случая: у вас есть бонус и, следовательно, снижение коэффициента на 5%;
вы стали виновником аварии и несете полную ответственность: у вас есть штраф и, следовательно, увеличение коэффициента на 25%;
вы вызвали аварию, но несете лишь частичную ответственность: у вас есть штраф и, следовательно, увеличение коэффициента на 12,5%.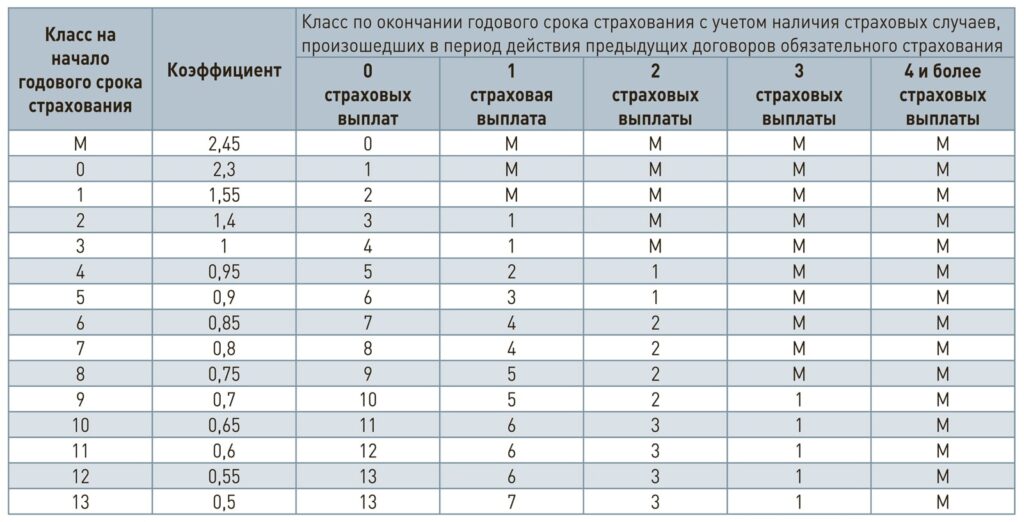
 04.2020 г. по 31.03.2021 г.;
04.2020 г. по 31.03.2021 г.;

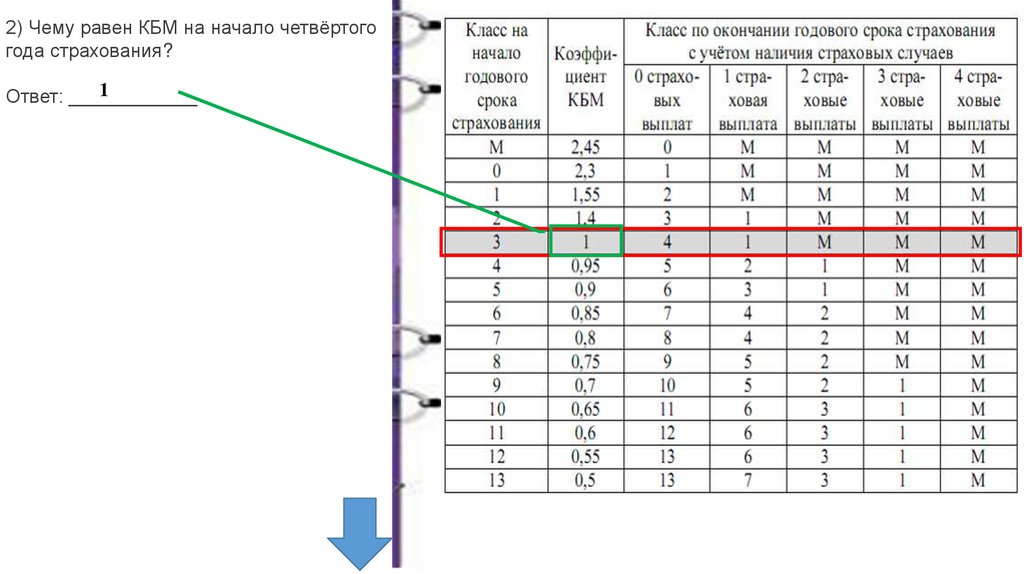 Каждому значению КБМ соответствует класс, который обозначается буквой или цифрой. М — максимальный класс, КБМ равен 3,92 с 1 апреля 2022 года. 0 — следующий по величине класс, КБМ равен 2,94 с 1 апреля 2022 года. 1 — еще на ступень ниже, КБМ равен 2,25 с 1 апреля 2022 года, и так далее до 13-го класса, КБМ для которого с 1 апреля 2022 года равен 0,46.
Каждому значению КБМ соответствует класс, который обозначается буквой или цифрой. М — максимальный класс, КБМ равен 3,92 с 1 апреля 2022 года. 0 — следующий по величине класс, КБМ равен 2,94 с 1 апреля 2022 года. 1 — еще на ступень ниже, КБМ равен 2,25 с 1 апреля 2022 года, и так далее до 13-го класса, КБМ для которого с 1 апреля 2022 года равен 0,46.
 2, стр. 92–107, 1976.
2, стр. 92–107, 1976.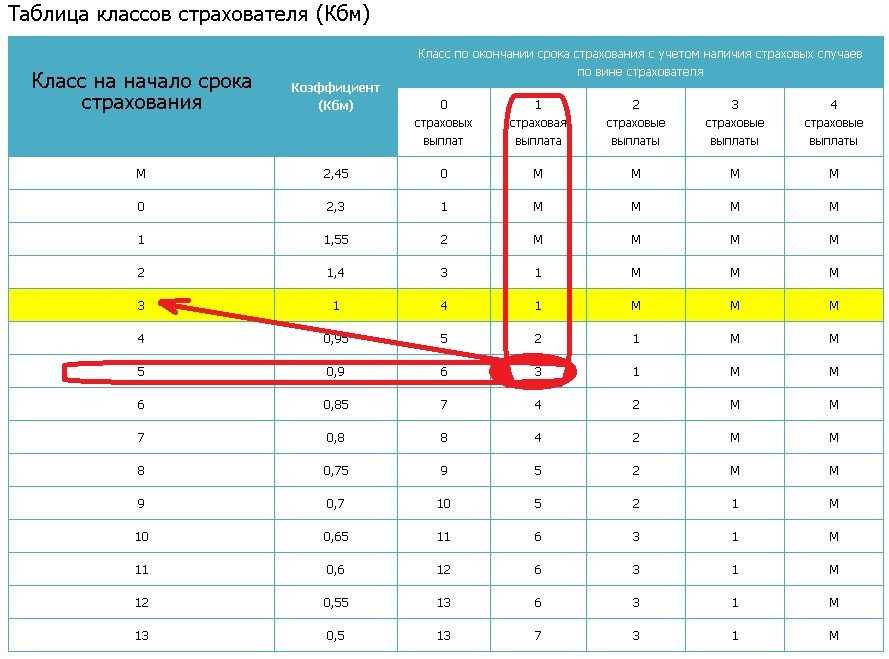 31, стр. 1–23, 2001.
31, стр. 1–23, 2001. Denuit, X. Marechal, S. Pitrebois, and J. F. Walhin, Acturial Modilling of Claimability Counts: Risk Classification, Trustity и Bomus-Malus Systems , Wiley, 2007.
Denuit, X. Marechal, S. Pitrebois, and J. F. Walhin, Acturial Modilling of Claimability Counts: Risk Classification, Trustity и Bomus-Malus Systems , Wiley, 2007.