Упражнение 8. Круговые движения туловищем в стороны. Книга советов на каждый день для мальчиков

Упражнение 8. Круговые движения туловищем в стороны. Книга советов на каждый день для мальчиков

ВикиЧтение

Книга советов на каждый день для мальчиков
Автор неизвестен

Содержание

Упражнение 8. Круговые движения туловищем в стороны

Этот прием помогает развить мышцы брюшного пресса и спины.

Ноги на ширине плеч, руки сцеплены в замок за головой. Двигаешь туловищем кругообразно в разные стороны, при этом нагибаясь и выпрямляясь.

При движении вниз – вдох, при подъеме – выдох.

Повтор 15–20 раз в каждую сторону.

Сделай 2–3 подхода.

Данный текст является ознакомительным фрагментом.

Упражнение 2.

Разведение рук в стороны назад

Упражнение 2. Разведение рук в стороны назад
Ноги на ширине таза, руки впереди, ладонями внутрь. Разведи руки, чтобы сошлись лопатки, затем вернись в исходное положение.Повтор 6—10 раз. Вдох при разведении рук, выдох – в исходном положении.Сделай 2

Упражнение 6. Разгибание рук в стороны

Упражнение 6. Разгибание рук в стороны
Ноги на ширине таза, эспандер за спиной, руки у плеч, ладонями наружу. Разводи руки в стороны, пока они не выпрямятся. Затем возврат в исходное положение.Вдох на разгибании, выдох при возврате в исходное положение.Повтор 10–15 раз.Сделай

Упражнение 8. Наклоны туловища в стороны

Упражнение 8. Наклоны туловища в стороны
Ноги прямые, ступня продета в ручку эспандера, свободная ручка захвачена рукой снизу.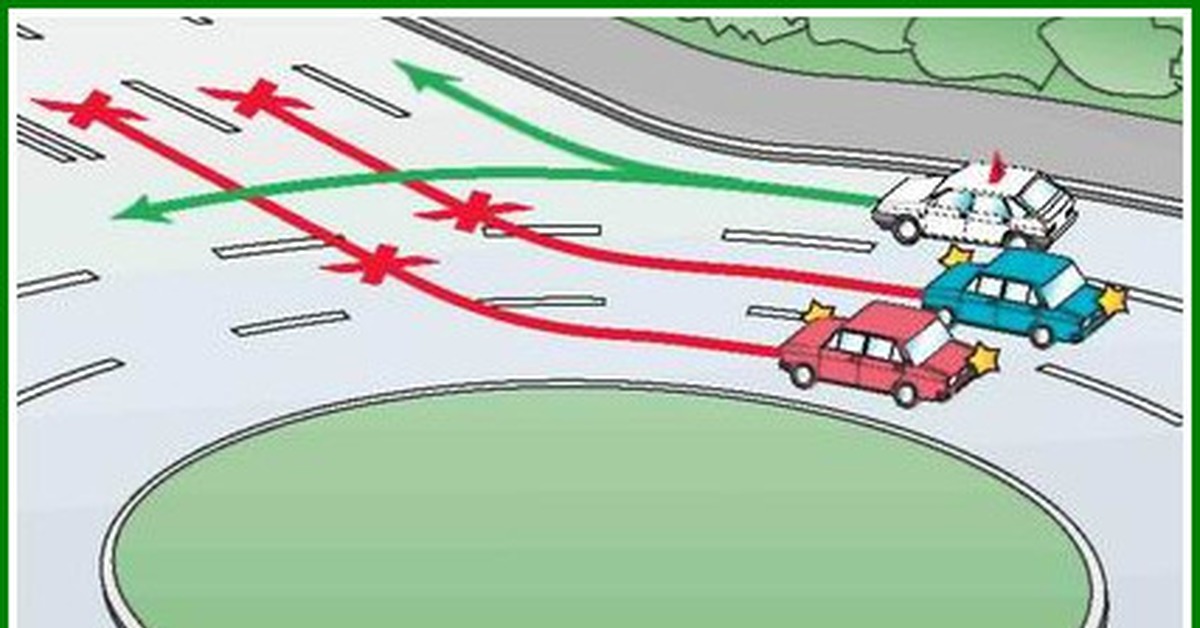 Сгибай руку по направлению к плечу. Теперь наклонись в сторону (вправо, если это правая рука). Левой рукой можешь удерживать правую у плеча. Затем

Упражнение 9. Опускание рук через стороны

Упражнение 9. Опускание рук через стороны
Ноги на ширине таза, руки с эспандером над головой ладонями наружу. Разводи руки в стороны так, чтобы эспандер двигался вниз за спиной. Затем медленно поднимай руки вверх и возвращайся в исходное положение.Вдох в начале упражнения,

Упражнение 10. Круговые движения ногами

Упражнение 10. Круговые движения ногами
Упражнение направлено на развитие мышц брюшного пресса.Ложись на спину, руки вытянуты вверх. Для хвата тебе понадобится какой-то тяжелый и неподвижный предмет – например, ножка дивана. Поднимай сведенные вместе ноги и делай

Упражнение 11.

Упражнение для развития мышц ног и таза

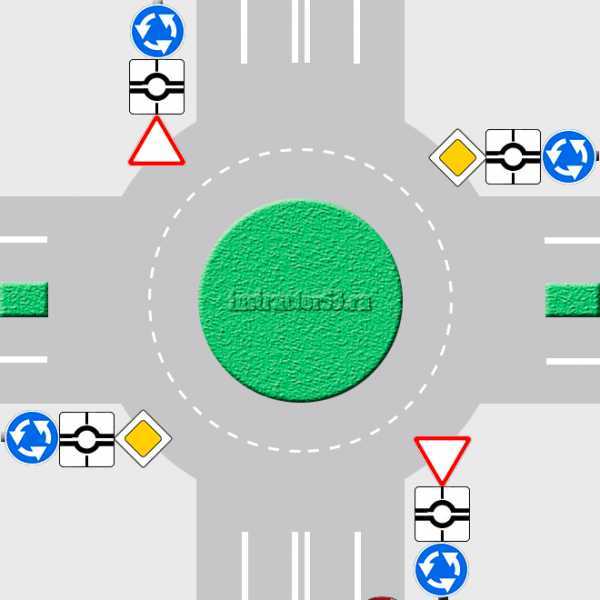
Упражнение 11. Упражнение для развития мышц ног и таза
Это довольно веселое и шумное упражнение, так что советую тебе подстелить на пол плотный коврик, чтобы не беспокоить соседей.Возьми табурет, залезь на него, спрыгни и затем продолжай совершать прыжки, стараясь достичь

Упражнение 1. Наклоны туловища в стороны

Упражнение 1. Наклоны туловища в стороны
Упражнение развивает мышцы туловищаВес гантелей 1–5 кг.Ноги на ширине таза, руки с гантелями вытянуты вдоль туловища. Наклоняешься как можно ниже вправо, левую руку сгибаешь в локте. Затем наклоняешься влево, сгибая правую

Упражнение 3. Поднимание рук – в стороны и вверх

Упражнение 3. Поднимание рук – в стороны и вверх
Упражнение укрепляет дельтовидные мышцыВес гантелей 2–7 кг.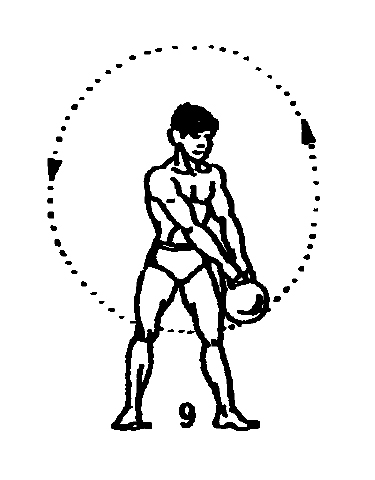 Ноги на ширине таза, руки вытянуты вдоль туловища, ладони к бедрам. Поднимай руки над головой и возвращай их в исходное положение.При подъеме вдох, при опускании

Упражнение 4. Круговые движения руками

Упражнение 4. Круговые движения руками
Данный прием помогает развить дельтовидные и грудные мышцы.Вес гантелей 1–2 кг.Ноги на ширине таза, руки с гантелями разведены в стороны ладонями вперед. Совершай круговые движения, стараясь двигать руками как можно дальше вперед и

Первые движения

Первые движения
Понаблюдайте за своим крошечным свертком, свернувшимся в люльке. Такой безмятежный, такой спокойный. Трудно поверить, что это тот же самый ребенок, который вертелся и выкидывал коленца у вас в животе. Вот он проснулся – переверните его и посмотрите на него

Движения в два месяца

Движения в два месяца
Расслабление рук и кистей.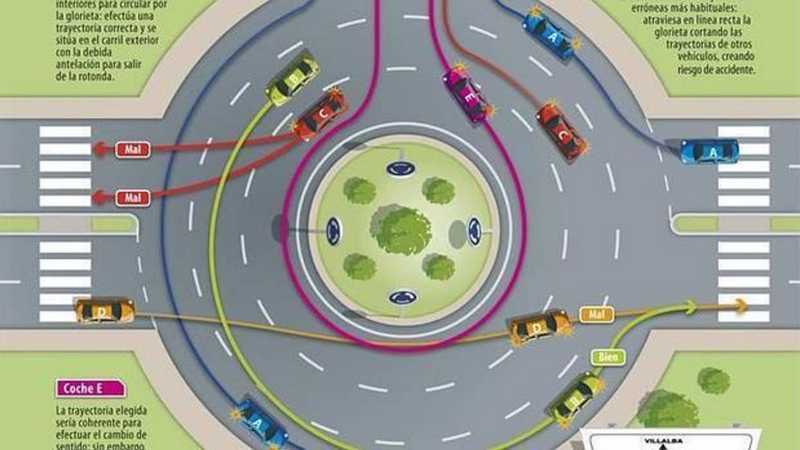 Стиснутые кулачки и прижатые к туловищу ручки, наблюдавшиеся на первом месяце, на втором несколько расслабляются, словно рефлексы, удерживавшие мышцы ребенка в сильном напряжении, оказываются пересиленными развивающимся

Движения в три месяца

Движения в три месяца
Положите ребенка на животик на стол или на пол, подложив что-то мягкое. Опуститесь рядом с ним. Поймайте его взгляд и начинайте говорить. Ребенок может поднять голову на сорок пять градусов или больше и вести беседу лицом к лицу. Вместо того чтобы

Движения месяца

Движения месяца
Ребенок начинает переворачиваться. Когда ваш ребенок начнет переворачиваться, больше зависит от темперамента ребенка, чем от двигательного развития. Очень активные дети, которые обожают выгибать спину дугой, склонны к тому, чтобы начать

Движения

Движения
Невербальный язык тела информативен не менее самих вопросов и интонации. Вместе с нами говорят жесты, мимика, движения, осанка. Если учитель спрашивает: «Какой это уровень?» – с нахмуренными бровями, скрещенными на груди руками, напряженным телом и суровым

как подготовить себя к тренировке (видео)

РАЗМИНКА ПЕРЕД БЕГОМ: КАК ПОДГОТОВИТЬ СЕБЯ К ТРЕНИРОВКЕ

Разминка перед бегом комплексно готовит организм к нагрузке: ускоряется обмен веществ, работа органов кровообращения и дыхания, увеличивается эластичность мышц и связок, в кровь поступают необходимые гормоны.

Органы и системы организма инертны и не сразу начинают действовать на том функциональном уровне, который необходим для тренировки или соревнований, что может приводить к травмам. После разминки тело лучше реагирует на физическую нагрузку, риск получить травму снижается.

Беговую разминку рекомендуем делать после 10 минут лёгкой трусцы, когда вы уже немного «разогрелись». Иными словами: начните бежать, через несколько минут разомнитесь, после чего продолжайте тренировку. Вот основные упражнения для разминки перед бегом.

Cпецпроект Ногибоги и adidas Runners Kyiv

УПРАЖНЕНИЯ ДЛЯ ШЕИ

Ноги на ширине плеч, подбородок прижмите к шее. Делайте плавные движения головой от правого плеча к левому и обратно. Голову не запрокидывайте.

Повторить:
3-5 раз.

Поверните голову максимально вправо. Через пару секунд вернитесь в исходное положение. Повторите в другую сторону. Следите чтобы подбородок все время был на одном уровне.

Повторить: по 2-3 раза в каждую сторону.

Максимально наклоните голову вниз и прижмите подбородок к груди — так, чтобы мышцы задней части шеи растянулись. Задержитесь в этом положении на несколько секунд. Затем тяните подбородок вверх, не запрокидывая голову назад.

Повторить: 2-3 раза.

КРУГОВЫЕ ДВИЖЕНИЯ ПЛЕЧАМИ

ВРАЩЕНИЕ ГОЛОВОЙ

ПОВОРОТЫ ГОЛОВЫ ВПРАВО И ВЛЕВО

НАКЛОНЫ ГОЛОВЫ ВВЕРХ И ВНИЗ

Медленно отводите плечи назад: сначала поднимая вверх к ушам, затем постепенно опуская вниз. То же самое в обратную сторону.

Повторить: 5 вращений в каждую сторону по 2-3 раза.

КРУГОВЫЕ ДВИЖЕНИЯ ПРЕДПЛЕЧЬЯМИ

Упражнение выполняется с согнутыми в локтях руками. Руки нужно вытянуть по сторонам, а затем выполнять круговые движения предплечьями.

Повторить: 10 раз.

КРУГОВЫЕ / МАХОВЫЕ ДВИЖЕНИЯ РУКАМИ

Можно делать такие движения одной рукой, двумя одновременно или попеременно. Амплитуда должна быть максимальной, а темп — плавным.

Повторить: 10 раз.

КРУГОВЫЕ ВРАЩЕНИЯ КОРПУСОМ, ВРАЩЕНИЯ ТАЗОМ

КРУГОВЫЕ ДВИЖЕНИЯ ПРЕДПЛЕЧЬЯМИ

НАКЛОНЫ КОРПУСА ВПРАВО И ВЛЕВО

Ноги на ширине плеч. Левая рука на поясе, правая вытянута вверх. Сделайте наклон влево, затем поменяйте руки и наклонитесь вправо. Можно вытянуть вверх обе руки, взяв их в замок, и проделать точно такие же наклоны.

Повторить: 10 раз.

КРУГОВЫЕ ДВИЖЕНИЯ РУКАМИ

КРУГОВЫЕ ВРАЩЕНИЯ КОРПУСОМ

Ноги на ширине плеч. Наклонитесь вправо, и, наподобие часовой стрелки, продолжайте плавное вращение корпуса по кругу. Таз и ноги при этом неподвижны.

Из этого положения можно выполнить круговые движения тазом — полезное упражнение для раскрепощения области вокруг крестца. Медленно делайте круговые движения тазом в правую сторону, с максимальной амплитудой, голова остается на месте, держим осанку. Затем то же самое в другую сторону.

Повторить: 10 вращений корпусом, 10 вращений тазом.

ПРУЖИНЯЩИЕ НАКЛОНЫ ВПЕРЁД

Ноги на ширине плеч. Наклонитесь, коснувшись руками пальцев ног. Сделайте пару плавных наклонов — с правой ноги на левую и наоборот. Следите, чтобы спина была ровной, а выпады не резкими.

Внимание: если у вас проблемы со спиной, не рекомендуем делать это упражнение.

Повторить: 10 раз.

ВЫПАДЫ С ПЕРЕКАТАМИ

КРУГОВЫЕ ВРАЩЕНИЯ КОРПУСОМ, ВРАЩЕНИЯ ТАЗОМ

ПОДНЯТИЕ КОЛЕНЕЙ

Это упражнение полезно для разогрева и разминки тазобедренного сустава. Выполните 5 круговых движений в одну сторону, затем — в другую. Повторите для другой ноги.

КРУГОВЫЕ ВРАЩЕНИЯ КОРПУСОМ

Поставьте ноги широко. Перенесите вес тела на правую ногу, одновременно сгибая её в колене. Затем сделайте перекат на левую ногу, после чего садитесь в глубокий выпад.

Из этого положения наклонитесь вперед, затем к прямой ноге, задерживаясь в каждом положении по 5 секунд и делая по 5 пружинистых движений вниз. Почувствуйте растяжение мышц (задней поверхности ног и отводящих). То же самое сделайте для другой ноги.

Повторить: по 2-3 раза для каждой ноги.

УПРАЖНЕНИЯ ДЛЯ СТОП

Эти упражнения подготовят голеностопные суставы к нагрузке. Выполните круговые движения стопой в каждую сторону по 5 до 10 раз. Затем — по 10 раз подъем с пятки на носок, прыжки на месте, вперёд-назад и в стороны.

ВЫПАДЫ С ПЕРЕКАТАМИ

ОБЩАЯ ПОДГОТОВКА К БЕГУ

Общая разминка непосредственно перед началом пробежки состоит из трёх упражнений: бег на месте с подниманием бедра, захлест голени и Джампинг Джеки. Выполняется для активизации деятельности сердечно-сосудистой системы, увеличения потребления кислорода, вентиляции лёгких. Выполняйте каждое упражнение в течение 30 секунд без отдыха. Сделайте от 3 до 4 подходов, между которыми отдыхайте максимум 30 секунд.

Разумеется, это далеко не все упражнения, а лишь основные, с которых вы можете начинать, постепенно увеличивая свой арсенал. Бегайте в своё удовольствие и будьте здоровы!

КРУГОВЫЕ ДВИЖЕНИЯ РУКАМИ

КРУГОВЫЕ ВРАЩЕНИЯ КОРПУСОМ

Математика кругового движения

Существуют три математические величины, которые будут представлять для нас наибольший интерес при анализе движения объектов по окружности. Этими тремя величинами являются скорость, ускорение и сила. Скорость объекта, движущегося по окружности, определяется следующим уравнением.

Ускорение объекта, движущегося по окружности, можно определить с помощью любого из двух следующих уравнений.

Уравнение справа (выше) получено из уравнения слева заменой выражения для скорости.

Суммарная сила ( F _сеть ), действующая на объект, движущийся по кругу, направлена ​​внутрь. Хотя на объект может действовать более одной силы, векторная сумма всех их должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если она есть), так что внешняя сила уравновешивается, а неуравновешенная сила направлена ​​в центр круга. Суммарная сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:0003

Уравнения в середине (вверху) и справа (вверху) получаются из уравнения слева заменой выражений для ускорения.

Этот набор уравнений кругового движения можно использовать двумя способами:

• как «рецепт» для решения алгебраических задач для решения неизвестной величины.
• как руководство к размышлению о том, как изменение одной величины повлияет на другую величину.

Эти два способа показаны ниже.

Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение для второго закона Ньютона определяет, как ускорение связано с результирующей силой и массой объекта.

Связь, выраженная уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. На самом деле, если бы результирующая сила увеличилась в 2 раза, уравнение предсказало бы, что ускорение увеличилось бы в 2 раза. Точно так же, если бы результирующая сила уменьшилась в 2 раза, уравнение предсказало бы, что ускорение ускорение уменьшилось бы в 2,9 раза.0003

Уравнение второго закона Ньютона также раскрывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0003

Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на другую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Предсказательная способность уравнения усложняется, когда одна из величин, входящих в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее результирующую силу ( F _net ) к скорости ( v ) объекта, движущегося в равномерном круговом движении.

Это уравнение показывает, что результирующая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. Для постоянной массы и радиуса F _сеть пропорциональна скорости ² .

Коэффициент изменения чистой силы равен квадрату коэффициента изменения скорости. Следовательно, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза. А если скорость объекта уменьшится вдвое (уменьшится в 2 раза), необходимая результирующая сила уменьшится в 4 раза.0003

Приведенные выше математические уравнения движения объектов по окружностям можно использовать для решения задач о движении по окружности, в которых необходимо определить неизвестную величину. Процесс решения задачи о круговом движении очень похож на любую другую задачу на уроках физики. Этот процесс включает в себя внимательное прочтение задачи, идентификацию известной и требуемой информации в переменной форме, выбор соответствующих уравнений, подстановку известных значений в уравнение и, наконец, алгебраические манипуляции с уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам о круговом движении.

Решение этой задачи начинается с идентификации известной и запрашиваемой информации.

Для определения ускорения автомобиля используйте уравнение a = v ² / R. Решение выглядит следующим образом:

Чтобы определить результирующую силу, действующую на автомобиль, используйте уравнение F _net = m•a. Решение заключается в следующем.

Решение этой задачи начинается с идентификации известной и запрашиваемой информации.

Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d — одна четвертая длины окружности, а время — 2,1 с. Решение выглядит следующим образом:

Для определения ускорения полузащитника воспользуемся уравнением a = v ² /R. Решение будет следующим:

Чтобы определить результирующую силу, действующую на полузащитника, используйте уравнение F _нетто = м•а. Решение заключается в следующем.

В уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных реальных сценариев движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.

Мы хотели бы предложить…

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.

Посетите:  Интерактивное  равномерное круговое движение || Моделирование горизонтального круга

1. Анна Литикал тренируется дома с демонстрацией центростремительной силы. Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу. Анна крутит ведро, когда оно наполовину наполнено водой и когда оно на четверть. В каком случае требуется большее усилие, чтобы вращать ведро по кругу? Объясните, используя уравнение как «руководство к мышлению».

2. Линкольн Континенталь и Юго делают поворот. Lincoln в четыре раза массивнее Yugo. Если они совершают поворот с одинаковой скоростью, то как соотносятся центростремительные силы, действующие на два автомобиля? Объяснять.

3. Cajun Cliffhanger в Great America – это аттракцион, в котором участники выстраиваются вдоль периметра цилиндра и вращаются по кругу с высокой скоростью. Когда цилиндр начинает вращаться очень быстро, пол убирается из-под ног гонщиков. Как влияет удвоение скорости на центростремительную силу? Объяснять.

4. Определить центростремительную силу, действующую на ребенка массой 40 кг, который делает 10 оборотов вокруг скалодрома за 29,3 секунды. Радиус ствола составляет 2,90 метра.

Перейти к следующему уроку:

4.4 Равномерное движение по окружности — University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
• Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
• Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
• Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.

Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.

Центростремительное ускорение

В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае меняется вектор скорости, или dv→/dt≠0.dv→/dt≠0. Это показано на рис. 4.18. Когда частица движется против часовой стрелки за время ΔtΔt по круговой траектории, вектор ее положения перемещается от r→(t)r→(t) к r→(t+Δt).r→(t+Δt). Вектор скорости имеет постоянную величину и касается пути при изменении от v→(t)v→(t) до v→(t+∆t),v→(t+∆t), меняя только свое направление. Поскольку вектор скорости v→(t)v→(t) перпендикулярен вектору положения r→(t),r→(t), треугольники, образованные векторами положения и Δr→,Δr→, и векторами скорости и Δv→Δv→ подобны. Кроме того, поскольку |r→(t)|=|r→(t+∆t)||r→(t)|=|r→(t+∆t)| и |v→(t)|=|v→(t+∆t)|,|v→(t)|=|v→(t+∆t)|, эти два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение

Δvv=ΔrrΔvv=Δrr или Δv=vrΔr.Δv=vrΔr.

Рисунок
4.18

(а) Частица движется по окружности с постоянной скоростью, с векторами положения и скорости в моменты времени tt и t+Δt.t+Δt. (b) Векторы скорости, образующие треугольник. Два треугольника на рисунке подобны. Вектор Δv→Δv→ указывает на центр окружности в пределе Δt→0,Δt→0.

Мы можем найти величину ускорения из

a=limΔt→0(ΔvΔt)=vr(limΔt→0ΔrΔt)=v2r.a=limΔt→0(ΔvΔt)=vr(limΔt→0ΔrΔt)=v2r.

Направление ускорения также можно найти, заметив, что когда ΔtΔt и, следовательно, ΔθΔθ приближаются к нулю, вектор Δv→Δv→ приближается к направлению, перпендикулярному v→. v→. В пределе Δt→0, Δt→0, Δv→Δv→ перпендикулярно v→.v→. Поскольку v→v→ касается окружности, ускорение dv→/dtdv→/dt указывает на центр окружности. Подводя итог, частица, движущаяся по окружности с постоянной скоростью, имеет ускорение величиной

.

ac=v2r.ac=v2r.

4,27

Направление вектора ускорения к центру окружности (Рисунок 4.19). Это радиальное ускорение называется центростремительным ускорением, поэтому мы обозначаем его индексом c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает «искать») и, таким образом, принимает значение «искание центра».

Рисунок
4.19

Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Вектор скорости также показан и касается окружности.

Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения.

Пример
4.10

Создание ускорения 1

g

Струя летит со скоростью 134,1 м/с по прямой линии и делает поворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение 1 g по направлению к центру круговой траектории?

Стратегия

Зная скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.

Раствор

Установите центростремительное ускорение равным ускорению свободного падения: 9,8 м/с2=v2/r.9,8 м/с2=v2/r.

Решая радиус, находим

r=(134,1м/с)29,8м/с2=1835м=1,835км. r=(134,1м/с)29,8м/с2=1835м=1,835км.

Значение

Чтобы создать большее ускорение, чем g на пилота, реактивный самолет должен будет либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.

Проверьте свое понимание
4,5

Маховик имеет радиус 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение 900,0 см/с2?900,0 см/с2?

Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в следующей таблице.

Объект	Центростремительное ускорение (м/с 2 или коэффициенты g )
Земля вокруг Солнца	5,93×10−35,93×10−3
Луна вокруг Земли	2,73×10−32,73×10−3
Спутник на геосинхронной орбите	0,233
Внешний край компакт-диска при воспроизведении	5. 785.78
Струя в бочке	(2–3 г )
Американские горки	(5 г )
Электрон, вращающийся вокруг протона в простой боровской модели атома	9,0×10229,0×1022

Стол
4.1

Типичные центростремительные ускорения

Уравнения движения для равномерного кругового движения

Частица, совершающая круговое движение, может быть описана вектором ее положения r→(t).r→(t). На рис. 4.20 показана частица, совершающая круговое движение против часовой стрелки. При движении частицы по окружности вектор ее положения заметает угол θθ с 9.

4,28

Здесь ωω — постоянная, называемая угловой частотой частицы. Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду. Угол θθ, который имеет вектор положения в любой конкретный момент времени, равен ωtωt.

Если T — это период движения, или время совершения одного оборота (2π2π рад), то

ω=2πT.ω=2πT.

Рисунок
4.20

Вектор положения частицы в круговом движении с его компонентами вдоль 9.

4,30

Из этого уравнения мы видим, что вектор ускорения имеет величину Aω2Aω2 и направлен против вектора положения, к началу координат, поскольку a→(t)=−ω2r→(t).a→(t)=−ω2r→(t ).

Пример
4.11

Круговое движение протона

Протон имеет скорость 5×106 м/с5×106 м/с и движется по окружности в плоскости xy радиусом r = 0,175 м. Какова его позиция в плоскости xy в момент времени t=2,0×10-7 с=200 нс?t=2,0×10-7 с=200 нс? В 9м.

Из этого результата мы видим, что протон расположен немного ниже оси x . Это показано на рис. 4.21.

Рисунок
4.21

Вектор положения протона при t=2,0×10-7с=200нс.t=2,0×10-7с=200нс. Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.

Значение

Мы выбрали начальное положение частицы на х- ось. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция при t = 200 нс.

Неравномерное круговое движение

Круговое движение не обязательно должно быть с постоянной скоростью. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.

При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы изменяется, то она имеет тангенциальное ускорение, равное скорости изменения величины скорости во времени:

аТ=d|v→|dt.aT=d|v→|dt.

4,31

Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение, равное векторной сумме центростремительного и тангенциального ускорений:

а→=а→с+а→Т. а→=а→с+а→Т.

4,32

Векторы ускорения показаны на рис. 4.22. Обратите внимание, что два вектора ускорения a→ca→c и a→Ta→T перпендикулярны друг другу, причем a→ca→c в радиальном направлении, а a→Ta→T в тангенциальном направлении. Полное ускорение a→a→ указывает на угол между a→ca→c и a→T.a→T.

Рисунок
4.22

Центростремительное ускорение направлено к центру окружности. Тангенциальное ускорение касается окружности в месте нахождения частицы. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений, которые перпендикулярны.

Пример
4.12

Общее ускорение при круговом движении

Частица движется по окружности радиусом r = 2,0 м. В промежутке времени с t = 1,5 с до t = 4,0 с его скорость изменяется со временем в соответствии с

v(t)=c1−c2t2,c1=4,0 м/с,c2=6,0 м·s. v(t)=c1−c2t2,c1=4,0 м/с,c2=6,0 м·с.

Чему равно полное ускорение частицы при т = 2,0 с?

Стратегия

Нам даны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение. Направление центростремительного ускорения направлено к центру окружности. Найдем величину тангенциального ускорения, взяв производную по времени от |v(t)||v(t)| используя уравнение 4.31 и оценивая его в t = 2,0 с. Мы используем это и величину центростремительного ускорения, чтобы найти полное ускорение.

Раствор

Центростремительное ускорение равно

v(2,0 с)=(4,0−6,0(2,0)2)м/с=2,5 м/сv(2,0 с)=(4,0−6,0(2,0)2)м/с=2,5 м/с

ac =v2r=(2,5 м/с)22,0 м=3,1 м/с2ac=v2r=(2,5 м/с)22,0 м=3,1 м/с2

направлен к центру круга. Тангенциальное ускорение равно

aT=|dv→dt|=2c2t3=12,0(2,0)3м/с2=1,5м/с2.