Содержание
Частота вращения | это… Что такое Частота вращения?
ТолкованиеПеревод
- Частота вращения
-
Угловая скорость (синяя стрелка) в одну единицу по часовой стрелке
Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке
Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки
Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
- ,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]).
 В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.
В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:
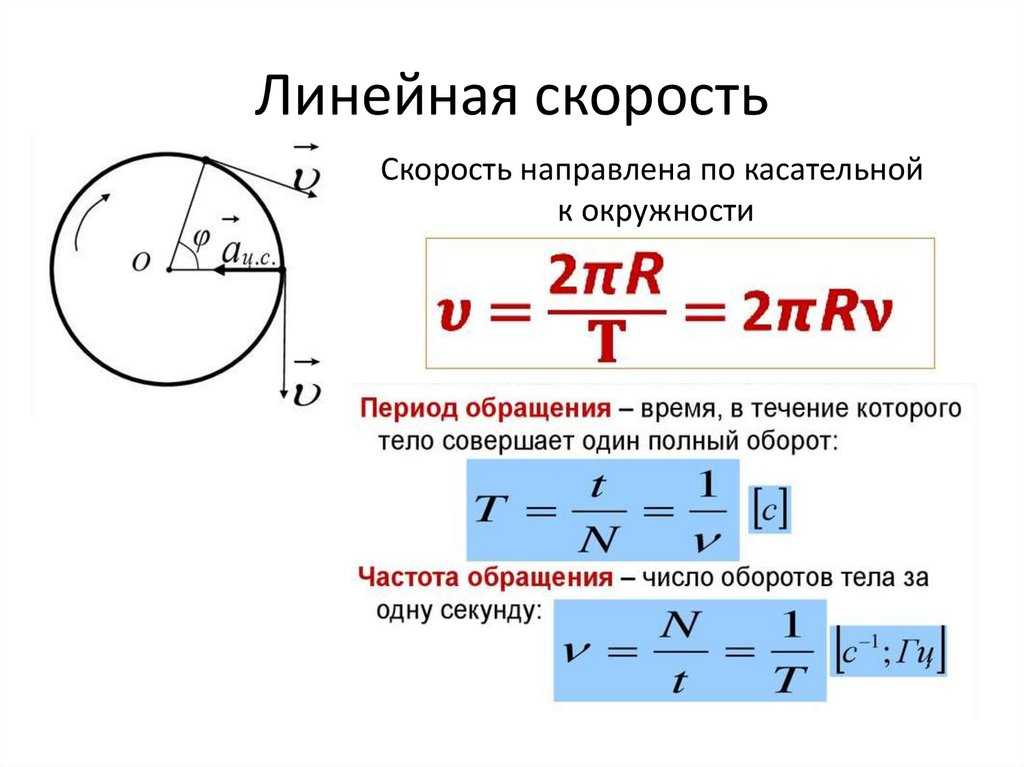
где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
- В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения.
 В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
- Производная угловой скорости по времени есть угловое ускорение.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
-
, где — радиус-вектор точки (из начала координат), — скорость этой точки.
 — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
— векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
- В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

- При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц) (то есть в таких единицах ).
- В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:
- Наконец, при использовании градусов в секунду связь с частотой вращения будет:
- Угловая частота
- Угловое ускорение
- Момент импульса
-
Wikimedia Foundation.
2010.
Игры ⚽ Поможем написать курсовую
- Частота сети
- Частота сердечных сокращений
Полезное
PhysBook:Электронный учебник физики — PhysBook
Содержание
-
1 Учебники -
2 Механика-
2. 1 Кинематика
1 Кинематика
-
2.2 Динамика -
2.3 Законы сохранения -
2.4 Статика -
2.5 Механические колебания и волны
-
-
3 Термодинамика и МКТ-
3.1 МКТ -
3.2 Термодинамика
-
-
4 Электродинамика-
4. 1 Электростатика
1 Электростатика
-
4.2 Электрический ток -
4.3 Магнетизм -
4.4 Электромагнитные колебания и волны
-
-
5 Оптика. СТО-
5.1 Геометрическая оптика -
5.2 Волновая оптика -
5.3 Фотометрия -
5.4 Квантовая оптика -
5. 5 Излучение и спектры
5 Излучение и спектры
-
5.6 СТО
-
-
6 Атомная и ядерная-
6.1 Атомная физика. Квантовая теория -
6.2 Ядерная физика
-
-
7 Общие темы -
8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТО
Геометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
период вращения
период вращения
| Астрофизика (Индекс) | О |
период вращения
Период вращения вращающегося тела это время
требуется один оборот, например, у Земли по существу день.
Скорость вращения тела является обратной величиной периода вращения,
например, Земля совершает по существу 1 оборот в день.
скорость вращения скорость движения тела
экватору, порядка 1000 миль в час для Земли.
Для нетвердого тела, такого как звезда, период вращения не является
один период времени, так как порции вращаются быстрее, чем другие порции,
называется дифференциальным вращением .
Что касается оборотов планеты (или оборотов планеты ),
день планеты (он же синодический период вращения ) состоит из
полный оборот плюс или минус часть оборота до точки
где та же сторона обращена к звезде-хозяину, учитывая их новое положение
в ходе их орбиты.
Таким образом, земные сутки в 86400 секунд длиннее, чем на самом деле.
период вращения около 86164 секунд ( период звездного вращения ).
Венера, которая вращается в направлении, противоположном своей орбите
( ретроградное вращение ),
имеет день, который короче периода его вращения.
Определение вращения внесолнечных планет представляет собой сложную задачу.
поэтому количество планет, для которых известно вращение, ограничено.
Вращение скалистых планет может представлять интерес для определения
их обитаемость.
Пульсары — нейтронные звезды, достаточно
компактный, чтобы быстро вращаться, некоторые имеют периоды вращения, составляющие мелкие доли
секунды (миллисекундные пульсары). Относительность накладывает ограничение на вращение
период объекта, потому что вращение не может быть таким быстрым
что любая часть объекта (например, его экватор) движется быстрее, чем
скорость света в вакууме, что накладывает ограничение на возможное вращение
скорость и период, в зависимости от размера объекта. На
открытие пульсаров, их часовая устойчивость повторяющегося
импульсы указывали на вращающийся источник, а подразумеваемое вращение
периоды были слишком малы для звезды главной последовательности, важно
подсказки к заключению, что они нейтронные звезды.
Если период вращения совпадает с периодом обращения и равен
проградный (т. е. не ретроградный), то же
е. не ретроградный), то же
сторона объекта постоянно обращена к своему хозяину
(если орбита круговая; если нет, т. е. орбита эксцентрична,
есть вариации относительно того, какая сторона обращена к хозяину)
которое называется синхронным вращением , признаком приливной блокировки.
Это верно для Луны, обращенной к Земле, и верно для большинства
луны в Солнечной системе.
Некоторые периоды вращения:
| Солнце | 25–35 (земных) дней (дифференциал). |
| Меркурий | 59 дней. |
| Венера | 243 дня (ретроградный). |
| Луна | 27,3 дня (синхронно). |
| Марс | 1,03 дня. |
| Юпитер | 0,41 дня (его интерьер). |
| Сатурн | 0,44 дня (его интерьер). |
| Уран | 0,72 дня. |
| Нептун | 0,67 дня. |
| Плутон |
6,39 дня.
|
| 51 Пегас б | 4,2 дня (синхронно). |
| Двоичный код Халса-Тейлора | 59 миллисекунд. |
| J1713+0747 | 4,57 мс. |
| Black Widow Pulsar | 1,61 мс. |
https://en.wikipedia.org/wiki/Rotation_period
Ссылка на страницы:
Ахернар
Ап звезда
Beta Pictoris b (β Pictoris b)
коричневый карлик (BD)
диаграмма цвет-период
модель гравитационного потенциала
гирохронология
Ячейка Хэдли
Хаумеа
Двоичный файл Халса-Тейлора (PSR B1913+16)
Дж 2
Парадокс Мейера
миллисекундный пульсар (MSP)
Диаграмма P-Pdot
производная периода
образование планет
пульсар (ПСР)
характерный возраст пульсара (τ)
вращающийся радиопереход (RRAT)
звездный
СМЦ Х-1
определение звездного возраста
определение звездных параметров
звездное вращение
Солнце
солнечное пятно
синхронная орбита
Звезда Т-Тельца (ТТС)
приливная блокировка
приливная миграция
Венера
Период вращения и продолжительность дня
|
./../spectrum.gif»> Астрономия онлайн eText : Небо Период чередования и продолжительность дня (Если вы боитесь математики, см. Использование математики в моих лекциях)
|
 В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
 — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
— векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

 1 Кинематика
1 Кинематика
 1 Электростатика
1 Электростатика
 5 Излучение и спектры
5 Излучение и спектры
 Это меняет видимое положение Солнца среди звезд, и в результате оно не перемещается по небу за тот же период времени, что и звезды. В зависимости от того, является ли вращение планеты прямым (в том же направлении, что и ее орбитальное движение) или обратным (в направлении, противоположном ее орбитальному движению), время, за которое Солнце делает один оборот по небу, называется синодический период вращения или продолжительность дня может быть длиннее или короче сидерического периода вращения. В таблице 1 показаны период вращения и продолжительность дня для Луны и планет. Как видите, для большинства тел эти два периода времени очень похожи, но для объектов с медленным периодом вращения, таких как Луна, Меркурий и Венера, существует большая разница между двумя периодами времени.
Это меняет видимое положение Солнца среди звезд, и в результате оно не перемещается по небу за тот же период времени, что и звезды. В зависимости от того, является ли вращение планеты прямым (в том же направлении, что и ее орбитальное движение) или обратным (в направлении, противоположном ее орбитальному движению), время, за которое Солнце делает один оборот по небу, называется синодический период вращения или продолжительность дня может быть длиннее или короче сидерического периода вращения. В таблице 1 показаны период вращения и продолжительность дня для Луны и планет. Как видите, для большинства тел эти два периода времени очень похожи, но для объектов с медленным периодом вращения, таких как Луна, Меркурий и Венера, существует большая разница между двумя периодами времени. 4,1 сек
4,1 сек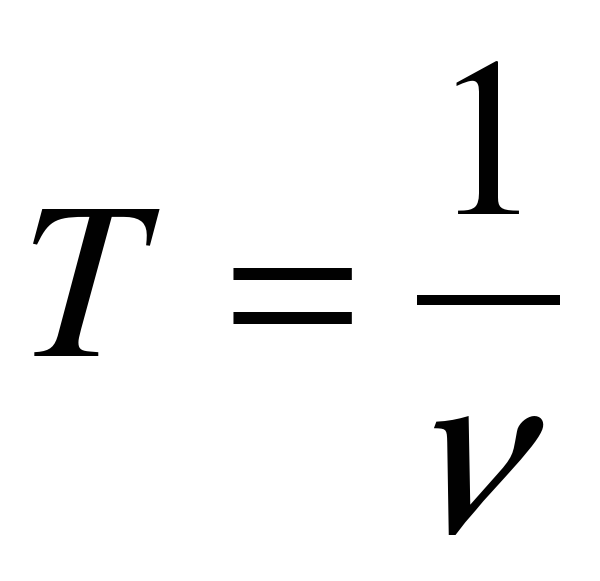 направление как орбитальное движение, так и РЕТРОГРАДНОЕ вращение, которое идет в противоположном направлении. Для этого мы определяем период вращения как время, за которое планета делает один оборот вокруг своей оси НА ВОСТОК, заставляя звезды поворачиваться вокруг неба на запад. Если бы планета вращалась в противоположном направлении, заставляя звезды вращаться вокруг неба в противоположном направлении, нам пришлось бы повернуть время вспять, чтобы увидеть движение звезд на запад. В результате период вращения планеты, имеющей ретроградное вращение, является отрицательным числом, как показано в таблице для трех планет, имеющих такое вращение.
направление как орбитальное движение, так и РЕТРОГРАДНОЕ вращение, которое идет в противоположном направлении. Для этого мы определяем период вращения как время, за которое планета делает один оборот вокруг своей оси НА ВОСТОК, заставляя звезды поворачиваться вокруг неба на запад. Если бы планета вращалась в противоположном направлении, заставляя звезды вращаться вокруг неба в противоположном направлении, нам пришлось бы повернуть время вспять, чтобы увидеть движение звезд на запад. В результате период вращения планеты, имеющей ретроградное вращение, является отрицательным числом, как показано в таблице для трех планет, имеющих такое вращение. Некоторые планеты (Венера, Уран и Плутон) вращаются на запад, если Северный полюс определяется как тот, что находится «наверху» планеты (над плоскостью нашей орбиты). Об этих планетах можно сказать, что они перевернуты (наклон больше 9°).0 градусов), или что они вращаются назад (наклон = отрицательное число) относительно своих орбит.
Некоторые планеты (Венера, Уран и Плутон) вращаются на запад, если Северный полюс определяется как тот, что находится «наверху» планеты (над плоскостью нашей орбиты). Об этих планетах можно сказать, что они перевернуты (наклон больше 9°).0 градусов), или что они вращаются назад (наклон = отрицательное число) относительно своих орбит. Поэтому, если вы не хотите рисковать совершить серьезные ошибки, вы должны быть уверены, что понимаете, что имеете в виду, когда указываете любое значение.
Поэтому, если вы не хотите рисковать совершить серьезные ошибки, вы должны быть уверены, что понимаете, что имеете в виду, когда указываете любое значение. На самом деле для большинства из них значения настолько близки, что они совпадают с точностью, показанной здесь. Однако для Луны и внутренних планет ситуация совершенно иная. Земля и Марс, которые вращаются относительно быстро, имеют разницу между периодом вращения и продолжительностью дня всего в несколько минут, но для Луны, Венеры и Меркурия разница между двумя значениями довольно велика. Для Луны разница в два дня недостаточна для того, чтобы день казался сильно отличающимся от периода вращения, но достаточно, чтобы сбить с толку, если причина разницы не понята, а для Меркурия и Венеры разница между двумя значениями настолько велика. что периоды их вращения, на первый взгляд, совершенно не связаны с продолжительностью их дней.
На самом деле для большинства из них значения настолько близки, что они совпадают с точностью, показанной здесь. Однако для Луны и внутренних планет ситуация совершенно иная. Земля и Марс, которые вращаются относительно быстро, имеют разницу между периодом вращения и продолжительностью дня всего в несколько минут, но для Луны, Венеры и Меркурия разница между двумя значениями довольно велика. Для Луны разница в два дня недостаточна для того, чтобы день казался сильно отличающимся от периода вращения, но достаточно, чтобы сбить с толку, если причина разницы не понята, а для Меркурия и Венеры разница между двумя значениями настолько велика. что периоды их вращения, на первый взгляд, совершенно не связаны с продолжительностью их дней.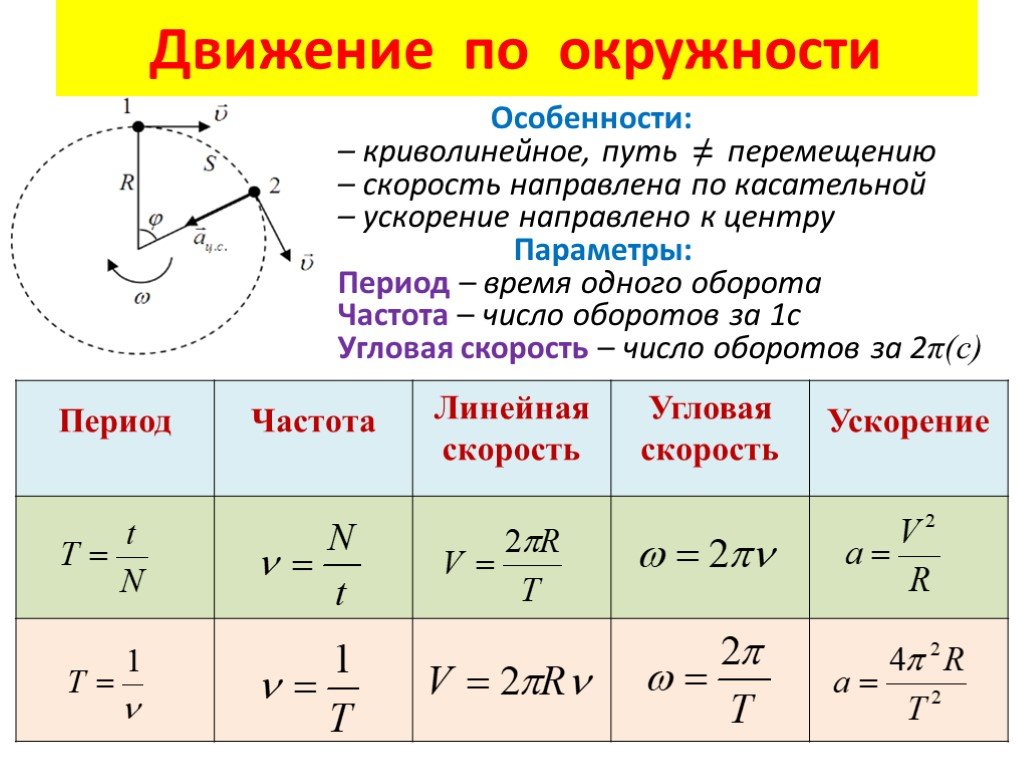 Число оборотов, которые сделала планета, указано цифрами справа от каждой точки. Белая точка показывает, как положение определенного места на планете изменяется по мере того, как планета вращается на восток (против часовой стрелки на этой диаграмме), а большая желтая точка в крайнем левом углу представляет положение Солнца. Размеры Солнца и планеты, а также угол, на который движется планета за один оборот, были преувеличены, чтобы было легче увидеть, что происходит.
Число оборотов, которые сделала планета, указано цифрами справа от каждой точки. Белая точка показывает, как положение определенного места на планете изменяется по мере того, как планета вращается на восток (против часовой стрелки на этой диаграмме), а большая желтая точка в крайнем левом углу представляет положение Солнца. Размеры Солнца и планеты, а также угол, на который движется планета за один оборот, были преувеличены, чтобы было легче увидеть, что происходит. В верхнем положении планета совершила один полный оборот, и планета и белая точка обращены в том же направлении, что и в начале, на что указывают горизонтальные линии, идущие влево от начального и конечного положений планеты. Если бы какие-либо звезды были видны, они совершили бы ровно один оборот по небу за один прошедший период вращения.
В верхнем положении планета совершила один полный оборот, и планета и белая точка обращены в том же направлении, что и в начале, на что указывают горизонтальные линии, идущие влево от начального и конечного положений планеты. Если бы какие-либо звезды были видны, они совершили бы ровно один оборот по небу за один прошедший период вращения.


 Таким образом, четырехминутная разница между продолжительностью дня и периодом вращения становится 4 умноженной на 750, или 3000 минут, что составляет немногим более двух дней.
Таким образом, четырехминутная разница между продолжительностью дня и периодом вращения становится 4 умноженной на 750, или 3000 минут, что составляет немногим более двух дней.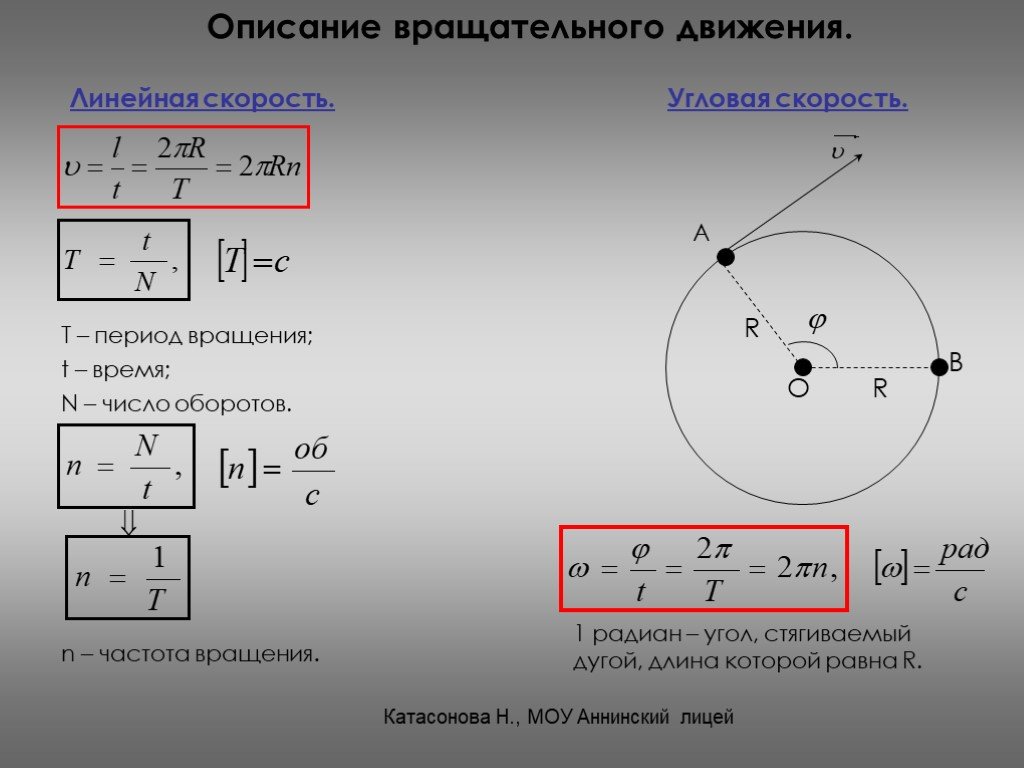 Но если нам нужны точные результаты для Меркурия и Венеры, которые вращаются еще медленнее и имеют более короткий период обращения, мы не сможем обойтись одной или двумя поправками; может потребоваться полдюжины или больше, в зависимости от желаемой точности. Поэтому для этих планет нам нужен другой способ расчета; но, к счастью, существует относительно простой способ вычисления разницы между периодом вращения и продолжительностью дня, который можно сделать сколь угодно точно, просто используя точные числа для выполнения арифметических действий.
Но если нам нужны точные результаты для Меркурия и Венеры, которые вращаются еще медленнее и имеют более короткий период обращения, мы не сможем обойтись одной или двумя поправками; может потребоваться полдюжины или больше, в зависимости от желаемой точности. Поэтому для этих планет нам нужен другой способ расчета; но, к счастью, существует относительно простой способ вычисления разницы между периодом вращения и продолжительностью дня, который можно сделать сколь угодно точно, просто используя точные числа для выполнения арифметических действий.
 Еще более удивительно, как обсуждалось в «Вращении Меркурия», когда Меркурий находится ближе всего к Солнцу в перигелии, его орбитальное и вращательное движение почти идентичны, так что более недели одна и та же сторона планеты обращена к кажущемуся неподвижным Солнцу. почти как если бы он всегда держался одной и той же стороны к Солнцу, как мы привыкли верить.
Еще более удивительно, как обсуждалось в «Вращении Меркурия», когда Меркурий находится ближе всего к Солнцу в перигелии, его орбитальное и вращательное движение почти идентичны, так что более недели одна и та же сторона планеты обращена к кажущемуся неподвижным Солнцу. почти как если бы он всегда держался одной и той же стороны к Солнцу, как мы привыкли верить. 22 Дни
22 Дни 36 36 36 3 36 3 36. ч 6,6 мин
36 36 36 3 36 3 36. ч 6,6 мин