Помогите найти период вращения Солнца вокруг своей оси. № 104. ГДЗ Физика 10 класс Рымкевич. – Рамблер/класс

Помогите найти период вращения Солнца вокруг своей оси. № 104. ГДЗ Физика 10 класс Рымкевич. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек экватора.
 

ответы

Радиус Солнца
R_c = 6,96 ∙ 10⁸ м.
Период обращения Солнца вокруг оси

Центростремительное ускорение точек экватора
 
Вычисления:

Ответ: Т = 25,3 суток; а_цс = 5,7 ∙ 10^-3 м/с².

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

ГДЗ по Физике Громов 10 класс, вопросы. Гл.4§22№4. . На чем основа- на гравиметрическая разведка?

Помогите ответить на вопрос Гл.4§22№4. 
На чем основана гравиметрическая разведка?
 

ГДЗ10 классГромов С. В.Физика

ГДЗ.Физика 11. класс.Рымкевич.Глава 10.Электрический ток в различных средах..Задание 859.Найти приблизительно температуру накала вольфрамовой нити.

Решите пожалуйста:
          На баллоне электрической лампы написано 220 В,
100 Вт. Для измерения сопротивления нити накала (Подробнее…)

ГДЗФизика11 классРымкевич А.П.

ГДЗ.Физика 11. класс.Рымкевич.Глава 10.Электрический ток в различных средах..Задание 865. Во сколько раз со- противление освещенного фоторезистора

Кто сможет решить ?
На рисунке 40 приведены графики зависимости силы
тока, идущего через фоторезистор, от приложенного (Подробнее…)

ГДЗФизика11 классРымкевич А.П.

Выполните деление. ГДЗ Математика 6 класс Чесноков. Дидактические материалы по математике для 6 класса. Вар.1 Вопр.161

Кто сможет? Выполните деление:
  (Подробнее…)

ГДЗМатематика6 классЧесноков А. С.

ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№45. Зад.№1.Под руководством Ященко. Помогите найти значение выражения.

Здравствуйте! Помогите найти значение выражения: (Подробнее…)

ГДЗЭкзаменыМатематикаЯщенко И.В.

470 Найти: 1) период обращения электрона на первой боровской орбите ат… — Учеба и наука

20. 09.14 Лучший ответ по мнению автора

Посмотреть всех экспертов из раздела Учеба и наука > Физика

Ядро атома гелия, имеющее массу. ..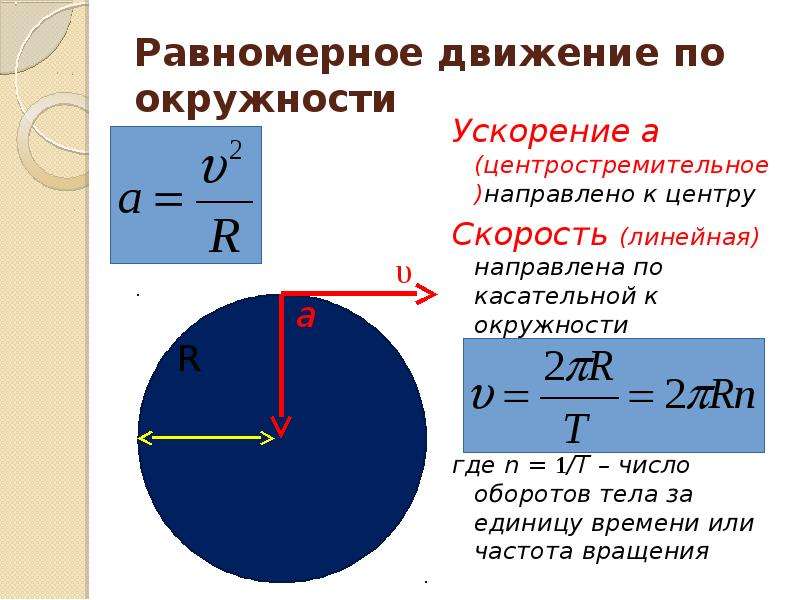

Решено

физка

Сколько миллиметров содержится в объеме,равном 38600 кубических мм?

На рисунке представлено положение четырёх тел с различными массами на разных расстояниях от поверхности Земли. Вопрос: Какое из этих тел имеет наибольший запас потенциальной энергии?

Решено

На проводник длинной 20 см,расположенный перпендикулярно вектору магнитной индукции, действует сила 0,6 Н, индукция магнитного поля 0,3 Тл. Найдите…

Пользуйтесь нашим приложением

6.1 Угол вращения и угловая скорость – Колледж физики, главы 1-17

6 Равномерное круговое движение и гравитация

Сводка

• Задайте длину дуги, угол поворота, радиус кривизны и угловую скорость.
• Рассчитайте угловую скорость вращения колеса автомобиля.

В главе 2 «Кинематика» мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. В главе 3 «Двумерная кинематика» речь шла о движении в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.

Когда объекты вращаются вокруг некоторой оси — например, когда CD (компакт-диск) на рис. 1 вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Мы определяем угол поворота [латекс]\boldsymbol{\Delta\theta}[/латекс] как отношение длины дуги к радиусу кривизны:

[латекс]\boldsymbol{\Delta\theta\:=}[/latex][латекс]\boldsymbol{\frac{\Delta{s}}{r}}.[/latex]

Рисунок 1. Все точки на компакт-диске движутся по дугам окружности. Ямы вдоль линии от центра к краю все перемещаются на один и тот же угол Δ θ за время Δ t . Рис. 2. Радиус окружности повернут на угол Δ θ . Длина дуги Δ с описана на окружности.

Длина дуги [latex]\boldsymbol{\Delta{s}}[/latex] — это расстояние, пройденное по окружности, как показано на рисунке 2. Обратите внимание, что [latex]\boldsymbol{r}[/latex] равно радиус кривизны кругового пути.

Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса[латекс]\boldsymbol{r}. [/latex]Длина окружности равна[латекс]\boldsymbol{2\pi{r }}.[/latex]Таким образом, за один полный оборот угол поворота равен

[латекс]\boldsymbol{\Delta\theta\:=}[/латекс][латекс]\boldsymbol{\frac{2\pi{r}}{r}}[/latex][латекс]\boldsymbol{= \:2\пи}.[/латекс]

Этот результат является основой для определения единиц, используемых для измерения углов поворота, [латекс]\boldsymbol{\Delta\theta}[/latex], равных радианам (рад), определенных таким образом, что

[латекс]\boldsymbol{2\pi\textbf{ рад} = 1\textbf{ оборот}.}[/латекс]

Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1. 90}[/латекс] [латекс]\boldsymbol{\pi}[/латекс] Таблица 1. Сравнение угловых единиц.

. от центра вращения ( r ) .

Если[latex]\boldsymbol{\Delta\theta=2\pi\textbf{rad}},[/latex]то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. 0}[/латекс]в круге или одном обороте, соотношение между радианами и градусами, таким образом, равно 90}.[/латекс]

Как быстро вращается объект? Мы определяем угловую скорость [латекс]\boldsymbol{\omega}[/латекс] как скорость изменения угла. В символах это

[латекс]\boldsymbol{\omega\:=}[/латекс][латекс]\boldsymbol{\frac{\Delta\theta}{\Delta{t}}},[/latex]

, где угловой поворот[латекс]\boldsymbol{\Delta\theta}[/latex]происходит за время[латекс]\boldsymbol{\Delta{t}}.[/latex]Чем больше угол поворота в данном время, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).

Угловая скорость[латекс]\boldsymbol{\omega}[/latex]аналогична линейной скорости[латекс]\boldsymbol{v}.[/latex]Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим яму на вращающемся компакт-диске. Эта яма перемещается на длину дуги[латекс]\boldsymbol{\Delta{s}}[/latex]за время[латекс]\boldsymbol{\Delta{t}},[/latex] и поэтому имеет линейную скорость

[латекс]\boldsymbol{v\:=}[/латекс][латекс]\boldsymbol{\frac{\Delta{s}}{\Delta{t}}}. [/latex]

Из [латекс]\boldsymbol{\Delta\theta=\frac{\Delta{s}}{r}}[/latex] мы видим, что [латекс]\boldsymbol{\Delta{s}=r\Delta\theta }.[/latex]Подстановка этого выражения в выражение для[latex]\boldsymbol{v}[/latex] дает

[латекс]\boldsymbol{v\:=}[/латекс][латекс]\boldsymbol{\frac{r\Delta\theta}{\Delta{t}}}[/latex][латекс]\boldsymbol{= \:г\омега}.[/латекс]

Мы записываем это отношение двумя разными способами и получаем два разных понимания:

[латекс]\boldsymbol{v=r\omega\textbf{или}\omega\:=}[/latex][латекс]\boldsymbol{\frac{v}{r}}.[/latex]

Первое соотношение в [latex]\boldsymbol{v=r\omega\textbf{ или }\omega\:=\frac{v}{r}}[/latex] утверждает, что линейная скорость[latex]\boldsymbol{ v}[/latex]пропорциональна расстоянию от центра вращения, таким образом, она является наибольшей для точки на ободе (самая большая[latex]\boldsymbol{r}[/latex]), как и следовало ожидать. Мы также можем назвать эту линейную скорость[latex]\boldsymbol{v}[/latex]точки на ободе тангенциальная скорость . Второе соотношение в [latex]\boldsymbol{v=r\omega\textbf{ или }\omega\:=\frac{v}{r}}[/latex] можно проиллюстрировать, рассмотрев шину движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости[латекс]\жирныйсимвол{v}[/латекс]автомобиля. См. рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина. ]\boldsymbol{v=r\omega}.[/latex]Аналогично, шина большего радиуса, вращающаяся с той же угловой скоростью ([latex]\boldsymbol{\omega}[/latex]), будет производить большую линейную скорость ( [латекс]\boldsymbol{v}[/латекс]) для автомобиля.

Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω . Скорость протектора шины относительно оси v , такая же, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω , где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.

Пример 1: Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью [latex]\boldsymbol{15,0\textbf{ м/с}}[/latex](около[latex]\boldsymbol{54\textbf{ км /ч}}[/латекс]). См. рис. 4.

Стратегия

Поскольку линейная скорость обода шины равна скорости автомобиля, мы имеем[latex]\boldsymbol{v=15.0\textbf{ м/с}}.[ /latex]Радиус шины равен[latex]\boldsymbol{r=0,300\textbf{м}}.[/latex]Знание[latex]\boldsymbol{v}[/latex]и[latex]\ boldsymbol{r},[/latex]мы можем использовать второе соотношение в[latex]\boldsymbol{v=r\omega,\:\omega=\frac{v}{r}}[/latex]для вычисления углового скорость.

Решение

Для расчета угловой скорости воспользуемся следующим соотношением: r}}.[/latex]

Замена известных,

[латекс]\boldsymbol{\omega\:=}[/latex][латекс]\boldsymbol{\frac{15.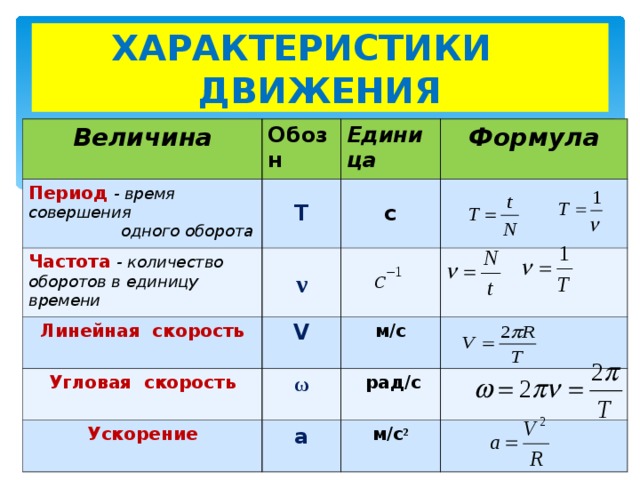 0\textbf{м/с}} {0.300\textbf{ м}}}[/latex][latex]\boldsymbol{=\:50.0\textbf{ рад/с}}.[/latex]

Обсуждение

Когда мы отменяем единицы в приведенном выше расчете, получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояния), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость

[латекс]\boldsymbol{\omega=(15,0\textbf{м/с})/(1,20\textbf{м})=12,5\textbf{рад/с}}.[/latex]

Оба [латекс]\boldsymbol{\omega}[/latex] и [латекс]\boldsymbol{v}[/latex] имеют направления (следовательно, они являются угловой и линейной скоростями , соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рисунке 5.

ЭКСПЕРИМЕНТ 9 ДЛЯ ДОМА0219

Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.

Рисунок 5. Поскольку объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.

ИССЛЕДОВАНИЯ PHET: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ

Рис. 6. Революция божьей коровки

Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.

• Равномерное круговое движение – это движение по окружности с постоянной скоростью. Угол поворота [латекс]\boldsymbol{\Delta\theta}[/латекс] определяется как отношение длины дуги к радиусу кривизны:
  90}.[/латекс]
• Угловая скорость[латекс]\жирныйсимвол{\омега}[/латекс]– скорость изменения угла,

  [латекс]\boldsymbol{\omega\:=}[/латекс][латекс]\boldsymbol{\frac{\Delta\theta}{\Delta{t}}},[/latex]

  , где вращение[латекс]\boldsymbol{\Delta\theta}[/latex]происходит за время[латекс]\boldsymbol{\Delta{t}}.[/latex]Угловая скорость измеряется в радианах в секунду. (рад/с). Линейная скорость[latex]\boldsymbol{v}[/latex]и угловая скорость[latex]\boldsymbol{\omega}[/latex]относительно

  [латекс]\boldsymbol{v=r\omega\textbf{или}\omega\:=}[/latex][латекс]\boldsymbol{\frac{v}{r}}.[/latex]

длина дуги

[латекс]\boldsymbol{\Delta{s}},[/latex]расстояние, пройденное объектом по круговой траектории

яма

крошечное углубление на спиральной дорожке, отформованной в верхней части поликарбонатного слоя компакт-диска

угол поворота

отношение длины дуги к радиусу кривизны на круговой траектории:

[латекс]\boldsymbol{\Delta\theta\:=}[/latex][латекс]\boldsymbol{\frac{\Delta{s}}{r}}[/latex]

радиус кривизны

радиус кругового пути

радиан

единица измерения угла

угловая скорость

[латекс]\boldsymbol{\omega},[/латекс]скорость изменения угла, под которым объект движется по круговой траектории

Вращение Сатурна

Имя:____________________________
Лабораторный отдел: Онлайн Дата: _____________

Разница
Между строк

Вы
будет использовать шкалу пластины ниже, чтобы преобразовать измерения в миллиметры на
фотография в нгстремы.

Вы будете работать с линиями поглощения
(темный) в спектре Сатурна, то есть самая центральная полоса света, содержащая
наклонные, темные линии. Яркие полосы выше и ниже планеты
сами по себе связаны с кольцами и будут игнорироваться для целей этого
лабораторное задание, заключающееся в определении скорости вращения планеты
Только. [Видите, все могло быть и хуже!] Выберите несколько таких наклонных линий для
ваши измерения, выбирая линии, которые четко определены и не слишком
широкий . Обозначьте выбранные вами линии цифрами 1, 2, 3… на фотографии.
Равномерно распределите выбранные линии по всему спектру.

Для
каждой линии, которую вы выбрали, вы сделаете два измерения — расстояние
каждый конец от наиболее удобной вертикальной контрольной линии. Возьмем разность
из этих двух расстояний (в миллиметрах), чтобы получить величину смещения между
свет исходит от противоположных краев диска планеты. Затем вы можете использовать
шкала пластины для преобразования разницы в миллиметрах в разницу в длине волны
(Dl или средний доплеровский сдвиг). Очередной раз
вы можете уменьшить ошибки, выбрав несколько линий и усредняя результаты.

50002

Уравнение для нахождения экваториальной скорости планеты Сатурн. Стандарт
Уравнение Доплера:

Здесь мы имеем небольшую
модификацию сделать, в связи с тем, что мы берем свет с допплеровским смещением
от каждой конечности планеты (в два раза), и свет
отражение от атмосферы Сатурна, чтобы достичь нас на Земле (дополнительный
коэффициент два). Тогда правильная форма для экваториальной скорости равна

(1)

Взятие
скорость света (с) как 300 000 километров в секунду, ваш ответ также будет в
единиц км/сек. Значение l _o = 6200
Ǻ будет служить с незначительной ошибкой в ​​рассматриваемой области.

Период вращения
отрезок времени, необходимый для того, чтобы точка на экваторе один раз перенеслась вокруг
вращение планеты. Это расстояние, которое он должен пройти, равно экваториальному.
окружности (2R) и движется со скоростью V, как определено выше.
Решение формулы скорость-расстояние-время для времени и замены d
и v, получаем период вращения:

(2)

1.