Линейная скорость через угловую, теория и онлайн калькуляторы

Линейная скорость через угловую, теория и онлайн калькуляторы

Определение

Мгновенной (истинной) скоростью ($\overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}=\frac{d\overline{r}}{dt}\ }\left(1\right).\]

$\Delta \overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $\Delta t$.

Выражение линейной скорости через угловую скорость

Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.

Так как вектор перемещения $\Delta \overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $\Delta \overline{r}$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.

Скорость прохождения пути ($s$) определяют:

\[v={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\left(2\right).\ }\]

Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.

Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($\varphi $), который образует радиус-вектор ($\overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).

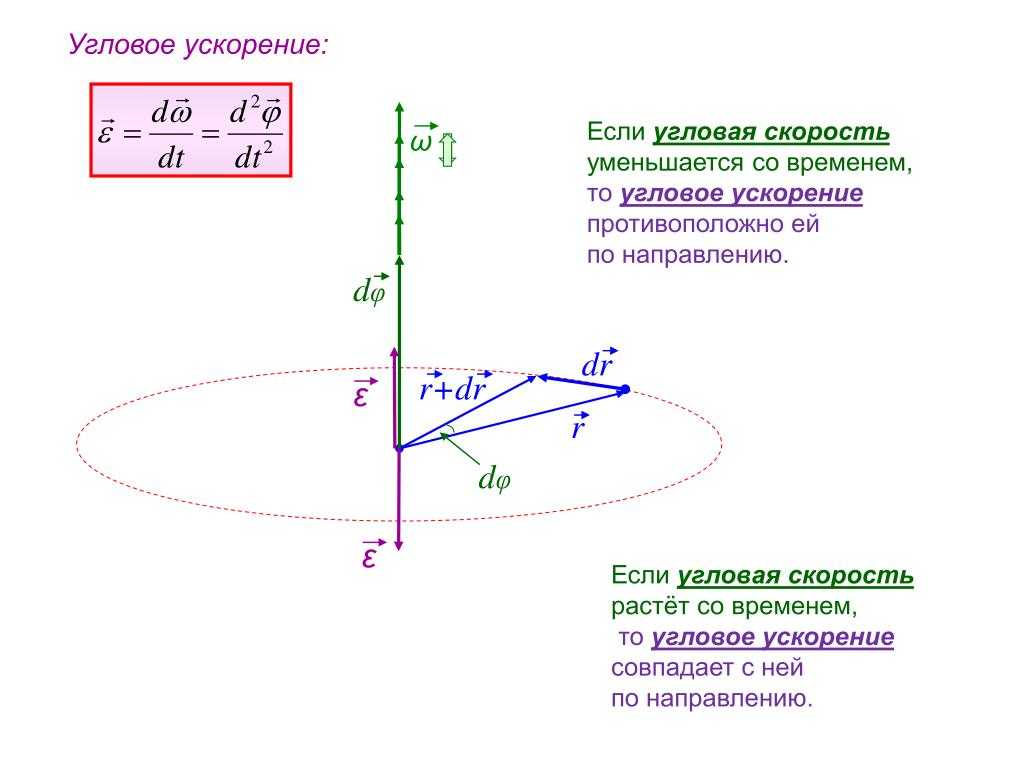
Быстроту изменения угла поворота $\varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $\omega $. Угловая скорость равна:

\[\omega =\frac{d\varphi }{dt}\left(3\right).\]

Вращение называют равномерным, если угловая скорость постоянна $\omega =const$.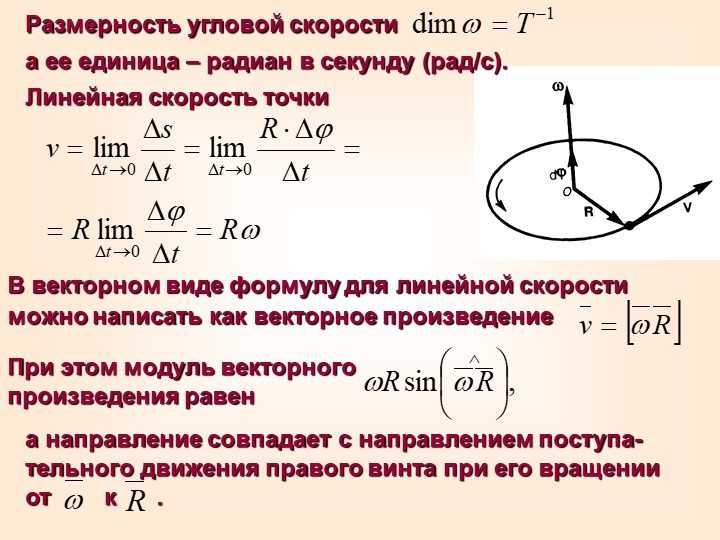 При равномерном вращении $\omega $ можно называть угловой частотой.

Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$\ R=const$, то длину дуги найдем как:

\[s=R\varphi \ \left(4\right).\]

Продифференцируем обе части выражения (4) по времени, имеем:

\[\frac{ds}{dt}=\frac{d\left(R\varphi \right)}{dt}=R\frac{d\varphi }{dt}\left(5\right).\]

Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:

\[v=R\omega \left(6\right).\]

Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ — радиус кривизны траектории в месте нахождения частицы.

В векторном виде выражение (6) записывают так:

\[\overline{v}=\overline{\omega }\times \overline{r}\left(7\right),\]

$\overline{r}$ — вектор, соединяющий ось вращения и движущуюся точку (рис.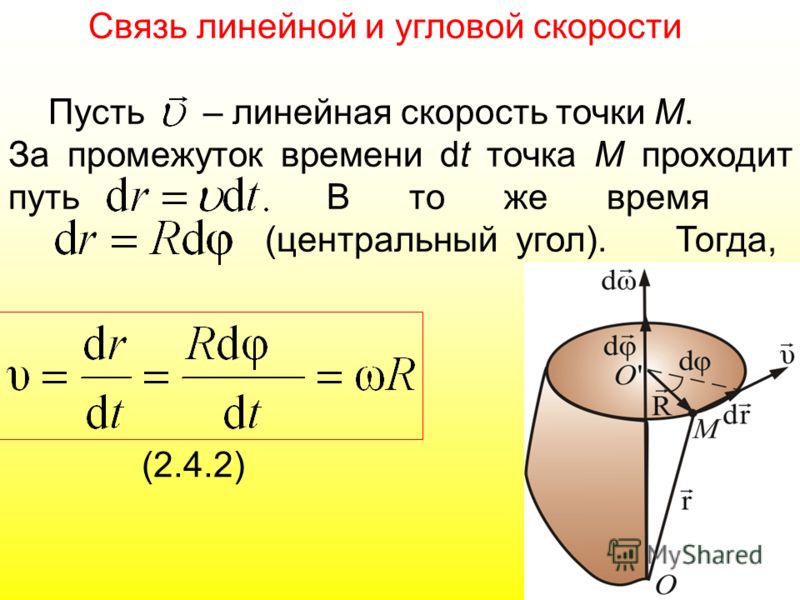 2). Модуль скорости, используя формулу (7) найдем как:

\[v=\omega r{\sin \alpha \ \left(8\right),\ }\]

где $\alpha $ — угол между вектором угловой скорости и $\overline{r}.$

Угловая скорость через линейную

Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:

\[\omega =\frac{v}{R}\left(9\right).\]

Или используя формулу (8) угловую скорость выразим как:

\[\omega =\frac{v}{r{\sin \alpha \ }}\left(10\right).\]

Примеры задач с решением

Пример 1

Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $\Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($\omega $)?

Решение.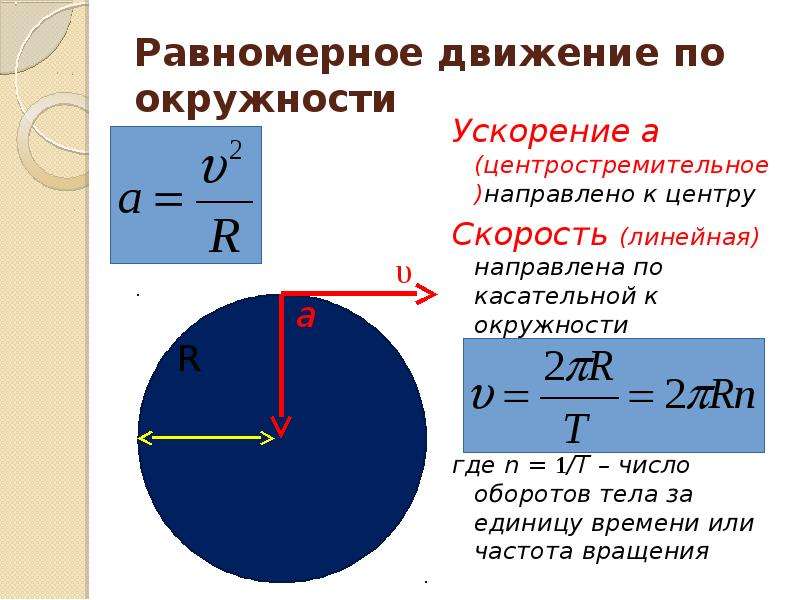 Основой для решения задачи будет формула:

\[\omega =\frac{v}{R}\left(1.1\right).\]

Угловые скорости движения точки A и B одинаковы (${\omega }_A={\omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):

\[{\omega }_A=\frac{v_1}{R_1};;\ {\omega }_B=\frac{v_2}{R_2}\left(1.2\right).\]

$R_1$ — расстояние от точки O до точки A; $R_2=R_1-\Delta l$ — расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:

\[\frac{v_1}{R_1}=\frac{v_2}{R_1-\Delta l}\to R_1=\frac{\Delta l\cdot v_1}{v_1-v_2}\left(1.3\right).\]

Найдем угловую скорость точки A:

\[{\omega }_A=v_1\cdot \frac{v_1-v_2}{\Delta l\cdot v_1}=\frac{v_1-v_2}{\Delta l}.\]

Ответ. Угловая скорость всех точек диска равна $\omega =\frac{v_1-v_2}{\Delta l}$

Пример 2

Задание. 2=15\ \left(\frac{м}{с}\right).\]

Ответ. $v\left(t’\right)=15\frac{м}{с}$

Читать дальше: масса и плотность вещества.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

4. Кинематика движения по окружности: задачи с ответами

(Все задачи по кинематике и ответы к ним находятся также в zip-архиве (332 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить все задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)

4.1.   Радиус рукоятки колодезного ворота в 3 раза больше радиуса вала, на который наматывается трос. Какова линейная скорость конца рукоятки, если ведро с глубины 10 м поднимается за 20 с?   [1,5 м/с]

4.2.   С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы центростремительное ускорение равнялось ускорению свободного падения?   [20 м/с]

4. 3.   Маховик делает 3 оборота в минуту. Найти угловую скорость вращения маховика.   [0,314 с⁻¹]

4.4.   Угловая скорость вращения лопастей колеса ветродвигателя 6 с⁻¹. Найти центростремительное ускорение концов лопастей, если их линейная скорость равна 20 м/с.   [120 м/с²]

4.5.   Период вращения платформы карусельного станка 3,14 с. Найти центростремительное ускорение крайних точек платформы, если ее диаметр 5 м.   [10 м/с²]

4.6.   Тело движется по окружности с постоянной скоростью 10 м/с. Определить изменение скорости тела за четверть периода; полпериода; период.   [14,15 м/с;  20 м/с;  0]

4.7.   Минутная стрелка часов в 1,5 раза длиннее часовой. Во сколько раз линейная скорость конца минутной стрелки больше конца часовой?   [в 18 раз]

4.8.   Какова скорость поезда, если его колеса, имеющие диаметр 1,2 м, делают 160 оборотов в минуту?   [10 м/с]

4. 9.   Определить скорость и ускорение точек поверхности Земли, находящихся на широте 30°. Радиус Земли равен 6400 км.   [400 м/с;  2,5 см/с²]

4.10.   Стержень длиной 50 см вращается вокруг оси перпендикулярной стержню. При этом линейные скорости концов стержня равны 10 см/с и 15 см/с. Найти угловую скорость вращения стержня.   [0,5 м/с]

4.11.   Через блок радиусом R = 50 мм, вращающийся вокруг горизонтальной оси, перекинута нить. Грузы, привязанные к концам нити, движутся с постоянной скоростью v = 20 см/с друг относительно друга. Определить угловую скорость вращения блока.   [2 Гц]

4.12.   Горизонтальная платформа радиусом 2 м равномерно вращается вокруг вертикальной оси с угловой скоростью 2,5 об/мин. По краю платформы шагает человек со скоростью 1 м/с относительно платформы. Определить ускорение человека, если он шагает; а) в направлении вращения; б) в противоположном направлении. [  1,15 м/с²;  0,12 м/с²]

4. 13.   Цилиндр радиусом R зажат между двумя параллельными рейками (рисунок слева). Рейки движутся параллельно самим себе с постоянными скоростями v₁ и v₂. Определить угловую скорость вращения цилиндра и линейную скорость его центра. Проскальзывания нет.

4.14.   Пропеллер самолета радиусом 1,5 м вращается с частотой 2000 об/мин. Скорость самолета относительно земли 162 км/ч. Определить скорость точки на конце пропеллера. Что представляет собой траектория движения этой точки?   [316 м/с]

4.15.   Скорость точки A вращающегося диска равна 50 см/с, а скорость точки B, находящейся на 10 см ближе к оси диска, равна 40 см/с. Определить угловую скорость вращения диска.   [1 с⁻¹]

4.16.   По горизонтальной дороге без проскальзывания катится тонкий обруч радиуса R со скоростью v_o (рисунок слева). Найти зависимость скорости точек обруча v от угла α.   [ v(α) = 2v_ocos α ]

4.17.   Диск катится без проскальзывания с постоянной скоростью v по горизонтальной дороге. Радиус диска равен R. Найти геометрическое место точек на диске, скорости которых в данный момент времени равны v.   [окружность радиусом R с центром в точке касания]

4.18.   Два диска связаны между собой шкивом. Левый диск крутится с угловой скоростью w. Определить линейную скорость точки A правого диска (рисунок слева).   [ v_A = wR₁R₂/R₃ ]

4.19.   Кривошип OA, вращаясь с угловой скоростью w = 2,5 с⁻¹, приводит в движение колесо радиусом r = 5 см, катящееся по неподвижному колесу радиусом R = 15 см. Найти скорость точки B (рисунок слева).   [ v_B = 2w(R + r) = 100 см/с ]

4.20.   Кривошип OA, вращаясь вокруг точки O, приводит в движение колесо 1 радиусом R = 20 см, катящееся по внутренней поверхности круга 2. Колесо 1, соприкасаясь с колесом 3, заставляет его вращаться вокруг точки O (рисунок слева). Во сколько раз угловая скорость колеса 3 больше угловой скорости кривошипа, если радиус колеса 3 равен r = 10 см?   [ w₃/w = 2(R + r)/r = 6 ]

4.21. Точка движется по окружности со скоростью v = at, где a = 0,5 м/с².   Найти ее полное ускорение в момент, когда она пройдет 0,1 длины окружности после начала движения.   [ a_p = a√(1 + 4π²)/5 = 0.8 м/с² ]

4.22.   Если колесо катится по горизонтальной дороге без проскальзывания, то траекторией любой точки обода колеса является линия, называемая циклоидой (рисунок слева). Определить радиус кривизны циклоиды в верхней точке, если радиус колеса R.   [ 4R ]

4. 23.   Малый радиус несущей части трамвайного колеса равен r, а большой радиус — R. Определить радиус кривизны циклоиды в верхней точке (рисунок слева).   [ (R + r)²/R ]

4.24.   По вертикальной цилиндрической проволочной спирали с постоянной скоростью v соскальзывает бусинка (рисунок слева). Определить ускорение бусинки, если радиус витков спирали равен R, а шаг спирали — h.   [ a = 4π²Rν²/(4π²R² + h²) ]

4.25.   Тело движется по окружности радиуса R со скоростью, которая зависит от времени по закону: v(t) = kt. Найти зависимость полного ускорения от времени.   [ a(t) = k√(1 + k²t⁴)/R) ]

4.26.   Через какое время встречаются минутная и часовая стрелки часов?   [около 1,09 ч; около 65,5 мин]

4.27.   Зависимость координат движущегося тела от времени имеют вид: x(t) = Rsin wt; y(t) = Rcos wt. Определить траекторию движения и ускорение тела.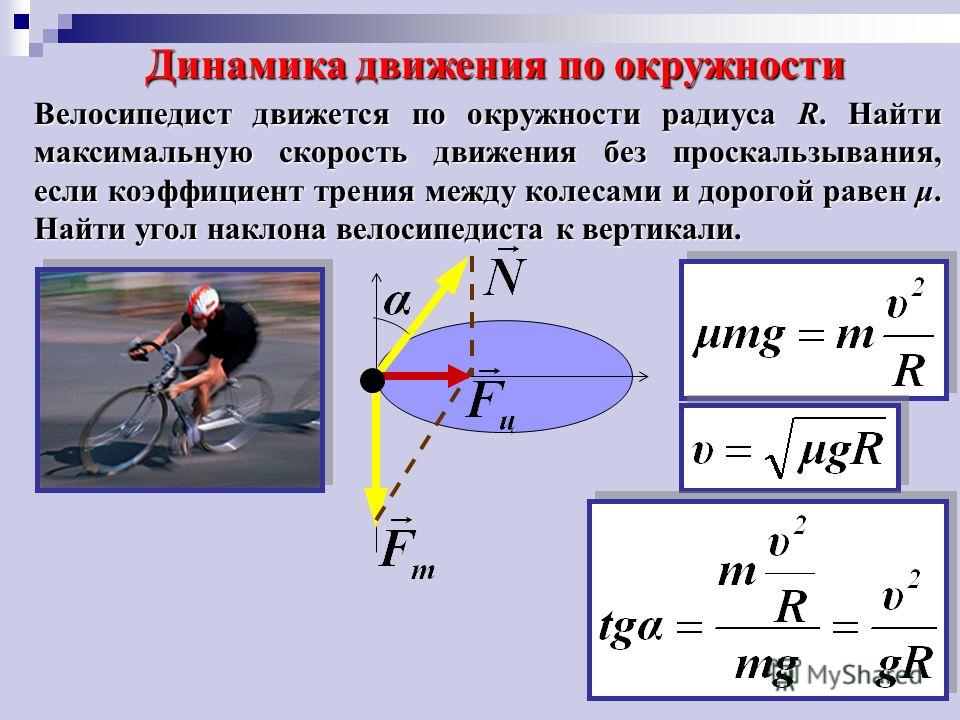   [окружность радиусом R; a = w²R ]

4.28.   Плоский обруч движется так, что в некоторый момент времени скорости концов диаметра AB лежат в плоскости обруча, перпендикулярны AB и равны v_A и v_B. Определить скорости точек C и D, если CD тоже диаметр перпендикулярный AB и эти скорости тоже лежат в плоскости обруча (рисунок слева).   [ v_С = v_D = √((v_A² + v_B²)/2) ]

4.29.   Точка начинает двигаться по окружности радиуса R с тангенциальным ускорением a. Как зависит от времени угол между векторами скорости и полного ускорения?   [ tg φ = at²/R ]

4.30.   При движении точки по окружности радиуса R центростремительное ускорение зависит от пройденного пути по закону a_ц = aS, где a — известная постоянная. Определить зависимость скорости точки от времени (v_o = 0).   [ v(t) = aRt/2 ]

4.31.   Тело брошено со скоростью v_o под углом α к горизонту. Определить среднюю за время полета угловую скорость вращения вектора скорости тела.   [ <w> = αg/(v_osin α) ]

4.32.   Направление вращения Земли вокруг своей оси совпадает с направлением ее вращения вокруг Солнца. Сколько суток было бы в году, если бы Земля вращалась вокруг своей оси в противоположную сторону?   [367 суток]

4.33.   Внешний радиус подшипника равен R, а радиус шариков — r. Подшипник катится по горизонтальной поверхности с постоянной скоростью v (рисунок слева). При этом внутренняя втулка не вращается. Определить угловую скорость вращения шариков. Проскальзывания нет.   [ w = v/(2r) ]

4.34.   Тело начинает двигаться по окружности из состояния покоя с равномерно возрастающей скоростью. Сколько оборотов сделает тело к моменту, когда центростремительное ускорение станет равно тангенциальному?   [ n = π/4;  примерно 0,8 оборота ] На правах рекламы: для специальной техники Volvo.

Далее: 40 задач по относительному движению и движению со связями.   |   Вернуться к списку разделов КИНЕМАТИКИ.

Связь угловой и линейной скорости с радиусом кругового пути

$\begingroup$

Линейная/тангенциальная скорость на круговой траектории увеличивается с увеличением радиуса и уменьшается с уменьшением радиуса. Следовательно, угловая скорость остается неизменной независимо от изменения радиуса (W=V/r). Однако, когда мы говорим о сохранении углового момента, мы говорим, что, поскольку импульс сохраняется, по мере увеличения радиуса линейная скорость должна уменьшаться, чтобы оставаться постоянной (поскольку L = mvr), из чего следует, что она обратно пропорциональна радиус, из чего следует, что угловая скорость обратно пропорциональна квадрату радиуса (когда фигурист сводит руки внутрь, они вращаются с большей угловой скоростью), но из сказанного выше ясно, что угловая скорость должна оставаться неизменной , независимо от того, каков радиус, не так ли? 92\омега\vec{e}_z,
$$
которую я написал здесь напрямую в зависимости от угловой скорости $\omega$.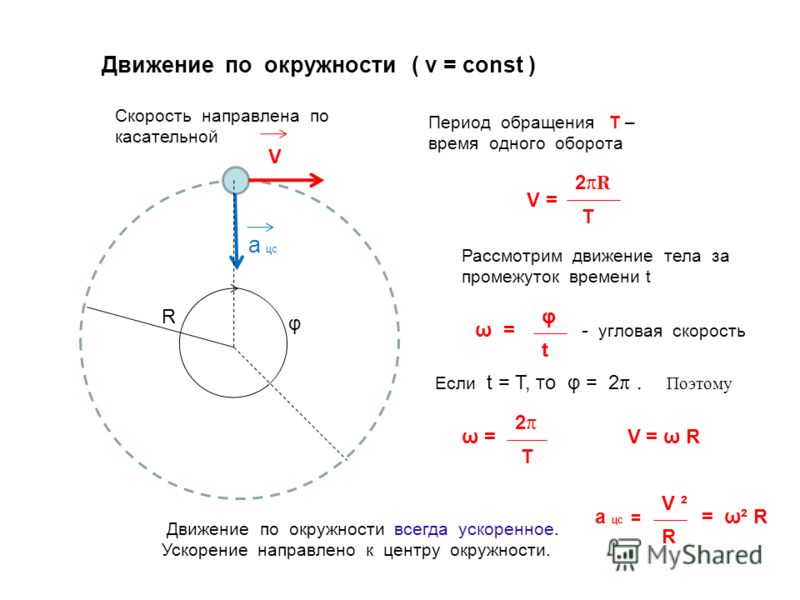 2}.
$$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

6.1 Угол поворота и угловая скорость

Цели обученияУгол вращенияУгловая скорость

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Определение длины дуги, угла поворота, радиуса кривизны и угловой скорости
• Рассчитать угловую скорость вращения колеса автомобиля

В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.

Угол поворота

Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (CD) на рис. 6.2 вращается вокруг своего центра — каждая точка объекта следует дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Определяем угол поворота
Размер ΔθΔθ 12{Δθ} {} должен быть отношением длины дуги к радиусу кривизны.

6.1 Δθ=Δср.Δθ=Δср. размер 12{Δθ= {{Δs} над {r} } } {}

Рис. 6.2 Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ размер 12{Δθ} {} за время ΔtΔt размер 12{Δt} {}.

Рисунок 6.3 Радиус окружности поворачивается на угол ΔθΔθ размером 12{Δθ} {}. Длина дуги ΔsΔs размером 12{Δs} {} описана на окружности.

Длина дуги ΔsΔs размер 12{Δs} {} — это расстояние, пройденное по круговому пути, как показано на рисунке 6.3. Обратите внимание, что rr размер 12{r} {} — это радиус кривизны кругового пути.

Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса rr размера 12{r} {}. Длина окружности равна 2πr2πr размера 12{2πr} {}. Таким образом, за один полный оборот угол поворота равен

.

6.2 Δθ=2πrr=2π.Δθ=2πrr=2π. size 12{Δθ= { {2πr} over {r} } =2π».»} {}

Этот результат является основой для определения единиц, используемых для измерения углов поворота, ΔθΔθ size 12{Δθ} {} в радианах (рад), определяемый таким образом, что

6,3 2πрад = 1 оборот. 2πрад = 1 оборот. размер 12{2π» рад «=» 1 оборот.»} {}

Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 6.1.

Таблица 6. 1 Сравнение угловых единиц

Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ размер 12{Δθ} {}), но точка 2 перемещается по дуге большей длины ΔsΔs размер 12{ влево (Δs вправо )} {}, поскольку она находится на большем расстояние от центра вращения (r)(r) размер 12{ \( r \) } {}.

Если Δθ=2πΔθ=2π size 12{Δθ=2π} {} рад, то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге или одном обороте есть 360º360º размера 12{«360″°} {}, соотношение между радианами и градусами, таким образом, равно

6,4 2πrad=360º2πrad=360º size 12{2π» rad»=»360″ rSup { size 8{ circ } } } {}

так, что

6,5 1rad=360º2π≈7π≈57,3º0,1rad . размер 12{1″ рад»= {{«360″ rSup {размер 8{круг} } } более {2π} } =»57» «.» 3 rSup { size 8{ circ } } «.»} {}

Угловая скорость

Как быстро вращается объект? Определим угловую скорость ωω величиной 12{ω} {} как скорость изменения угла. В символах это

6,6 ω=ΔθΔt,ω=ΔθΔt, размер 12{ω= {{Δθ} над {Δt} } «,»} {}

где угловой поворот ΔθΔθ размер 12{Δθ} {} происходит за время ΔtΔt размер 12{Δt} {}. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).

Угловая скорость ωω размера 12{ω} {} аналогична линейной скорости vv размера 12{v} {}. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается по дуге длиной ΔsΔs размером 12{Δs} {} за время ΔtΔt размером 12{Δt} {}, поэтому она имеет линейную скорость

6,7 v=ΔsΔt.v=ΔsΔt. размер 12{v= { {Δs} над {Δt} } «.»} {}

Из Δθ=ΔsrΔθ=Δsr размер 12{Δθ= {{Δs} над {r} } } {} мы видим, что Δs= rΔθΔs=rΔθ размер 12{Δs=rΔθ} {}. Подстановка этого выражения в выражение для размера vv 12{v} {} дает

6,8 v=rΔθΔt=rω.v=rΔθΔt=rω. size 12{v= {{rΔθ} над {Δt} } =rω». «} {}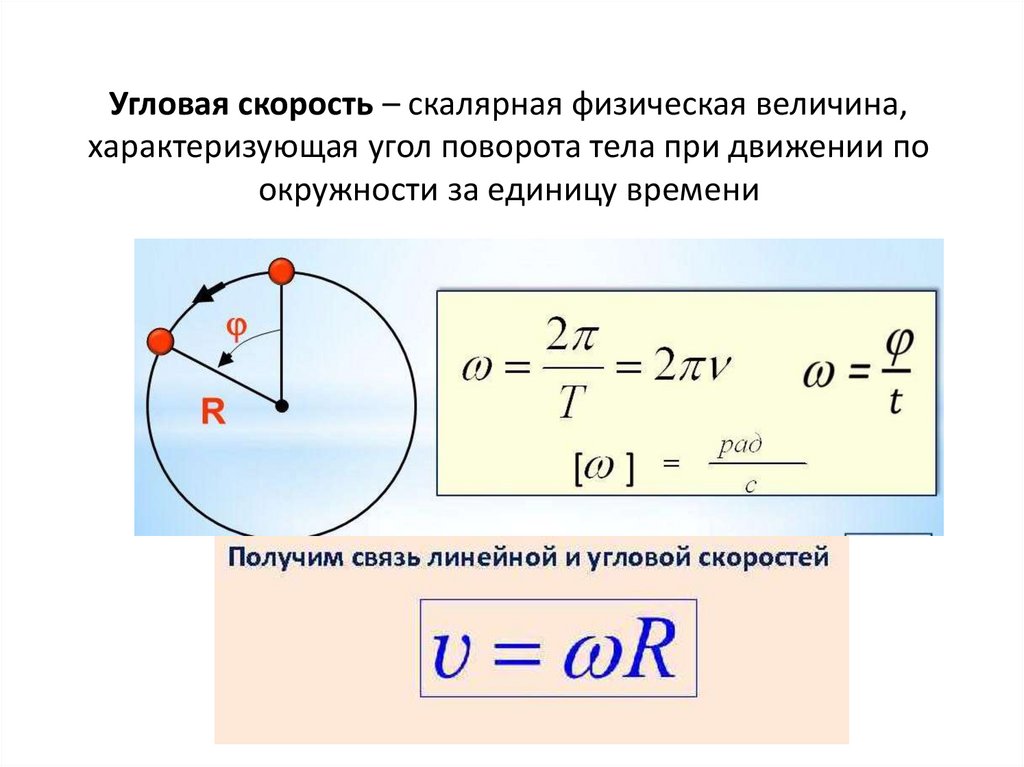

Мы запишем это соотношение двумя разными способами и получим два разных понимания

6,9 v=rω или ω=vr.v=rω или ω=vr. размер 12{v=rω«»или «ω= { {v} над {r} } «.»} {}

Первое соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω«»или «ω= { {v} over {r} } } {} утверждает, что линейная скорость vv размер 12{v} {} пропорционален расстоянию от центра вращения, поэтому он является наибольшим для точки на ободе (наибольший размер rr 12{r} {}), как и следовало ожидать. Мы также можем назвать эту линейную скорость vv размером 12{v} {} точки на ободе тангенциальной скоростью . Второе соотношение в v=rω или ω=vrv=rω или ω=vr size 12{v=rω«» или «ω= {{v} over {r}}} {} можно проиллюстрировать, рассмотрев шину движущаяся машина. Обратите внимание, что скорость точки на ободе шины такая же, как скорость vv размера 12{v} {} автомобиля. (см. рис. 6.5). Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой размер vv 12{v} {} означает большой размер ωω 12{ω} {}, потому что v=rωv=rω размер 12{v=rω} {}. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω размер 12{ω} {}), будет производить большую линейную скорость (vv размер 12{v} {}) для автомобиля.

Рисунок 6.5 Автомобиль, движущийся со скоростью vv размера 12{v} {} вправо, имеет шину, вращающуюся с угловой скоростью ωω размера 12{ω} {}. Скорость протектора шины относительно оси равна vv размер 12{v}{}, такой же, как если бы автомобиль был на домкрате. Таким образом, автомобиль движется вперед с линейной скоростью v=rωv=rω размер 12{v=rω} {}, где rr размер 12{r} {} — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.

Пример 6.1 Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с15,0 м/с Размер 12{«15» «.» 0`»м/с»} {} (около 54 км/ч54км/ч размер 12{«54″`»км/ч»} {}) (см. рис. 6.5.

Стратегия

Поскольку линейная скорость обод шины такой же, как скорость автомобиля, мы имеем
v=15,0 м/с. v=15,0 м/с. размер 12 {v} {}
Радиус шины принимается равным
r=0,300 м. r=0,300 м. размер 12{r} {} Зная
vv size 12{v} {} и rr size 12{r} {}, мы можем использовать второе соотношение в v=rω, ω=vrv=rω, ω=vr size 12{v=rω,«ω= { {v} над {r} } } {} для вычисления угловой скорости.

Решение

Для расчета угловой скорости воспользуемся следующим соотношением

6.10 ω=vr.ω=vr. размер 12{ω= { {v} над {r} } «.»} {}

Подстановка известных,

6,11 ω=15,0м/с0,300м=50,0рад/с.ω=15,0м/с0. 300 м = 50,0 рад/с. размер 12{ω= {{«15» «.» 0″ м/с»} более {0 «.» «300»» м»} } =»50″ «.» 0″ рад/с.»} {}

Обсуждение

Когда мы исключаем единицы измерения в приведенном выше расчете, мы получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны, поскольку определяются как отношение расстояния, мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с колесами гораздо большего размера, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, его колеса вращались бы медленнее.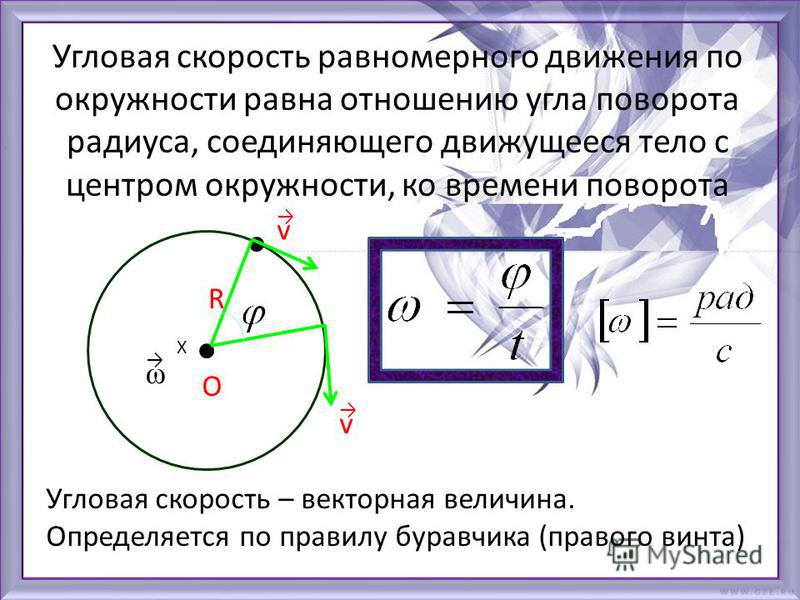 Они будут иметь угловую скорость

6,12 ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. ω=(15,0 м/с)/(1,20 м)=12,5 рад/с. размер 12{ω= \(«15» «.» 0`»м/с» \) / \( 1 «.» «20»`м \) =»12″ «.» 5`»рад/с.»} {}

Оба ωω размера 12{ω} {} и vv размера 12{v} {} имеют направления, следовательно, они являются угловой и линейной скоростями соответственно. Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рис. 6.6.

Эксперимент на вынос

Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (покачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.