Содержание
1.26. Среднее угловое ускорение
Из
анализа равенства (47) следует, что угловая
скорость
может изменяться как за счет изменения
линейной скорости v при вращении (в этом
случае угловая скорость изменяется по
величине), так и за счет поворота оси
вращения в пространстве. При неравномерном
вращении тела вокруг неподвижной оси
угловая скорость изменяется только по
величине, оставаясь постоянной по
направлению.
Если
при вращении (R = сonst) за некоторое время
t
угловая скорость получит приращение
,
то линейная скорость получит приращение
v,
т. е.
v
= R .
(51)
Разделим
правую и левую части равенствa (51) на
время t,
за которое произошло вращение, получим,
что
.
Отношение
(52)
– называют
средним угловым ускорением.
Средним угловым
ускорением тела называют отношение
изменения угловой скорости к промежутку
времени, в течение которого это изменение
произошло.
1.27. Мгновенное угловое ускорение
При
t
0 в пределе получим абсолютное значение
мгновенного углового ускорения:
(53)
т.
е. мгновенное угловое ускорение численно
равно первой производной угловой
скорости по времени или – второй
производной углового перемещения по
времени.
1.28. Связь линейного и углового ускорений
Используя равенство
(1.52) и переходя к пределу, получаем
.
Учитывая,
что
,
так как тангенциальное ускорение,
характеризует изменение скорости только
по величине имеем
а
= R
. (54)
(54)
В
СИ единицей измерения углового ускорения
является радиан на секунду в квадрате
(рад/c2
или с-2).
1.29. Связь линейных величин s, V, a c угловыми , ,
Полученные равенства
s
= R
,
v
= R
,
a
= R
(55)
показывают,
что линейные кинематические величины
s, v, a,
характеризующие
движение отдельных точек тела, получаются
умножением кинематических угловых
величин ,
,
,
отражающих
движение
всего тела в целом на расстояние от этих
точек до оси вращения (радиусы).
При вращательном
движении абсолютно твердого тела
линейные скорости точек тела направлены
по касательным к траекториям (окружности)
и непрерывно изменяют направление. При
равномерном вращении тела быстрота
изменения направления скорости
характеризуется нормальным ускорением
аn
==2
R. (56)
(56)
Вследствие
того, что для всех точек тела
= const,
аn
по абсолютной величине растет при
удалении от оси вращения. Используя
связь полного, нормального и касательного
ускорений и учитывая (1.54) и (1.56) имеем
.
(57)
Угловое ускорение
Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.
Основные понятия
Определение 1
Угловое ускорение – величина, характеризующая изменение скорости с течением времени.
Пусть рассматриваемый промежуток времени это: Δt=t1-t, а изменение угловой скорости составит Δω=ω1-ω, тогда числовое значение среднего углового ускорения за тот же интервал времени: ε=∆ω∆t=ε. Перейдем к пределу, когда Δt>0, тогда формула углового ускорения будет иметь вид: ε=lim∆t→0∆ω∆t=dωdt=d2φdt=ω˙=φ¨.
Определение 2
Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.
Размерность углового ускорения 1T2 (т.е. 1время2). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается рад/с2 или иначе: 1с2(с-2).
Определение 3
Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.
Определение 4
Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.
В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.
Рисунок 1. Вектор углового ускорения
Если мы представим угловое ускорение как вектор ε→=dω→dt, имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε→ и ω→ совпадут по направлениям (левая часть
рисунка 1) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка 1).
Закон равнопеременного вращения
Определение 5
Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным (ε=const).
Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t0 угол вращения равен ϕ=ϕ0; угловая скорость — ω=ω0 (т.е. ω0 является начальной угловой скоростью).
Выражение ε=dωdt=ω˙=φ¨ дает нам возможность сделать запись: dω=εdt. Проинтегрируем левую часть крайней записи в пределах от ω0 до ω, а правую – в пределах от 0 до t, тогда:
ω=ω0+εt, dφ=ω0dt+εtdt.
Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:
Определение 6
Закон равнопеременного вращения: φ=φ0+ωt+εt22.
Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.
Вращение является равнозамедленным, когда ω и ε противоположны по знаку.
Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R, тогда: αr=εR. Нормальное ускорение имеет также связь с угловым: an=ω2R. Учтем это выражение и для полного ускорения получим: a=ar2+an2=Rε2+ω4 Для равнопеременного движения: ω=εt; an=ω2R=ε2t2R и a=Rε2+ε4t4=Rε1+ε2t4.
Пусть некоторая точка вращается неравномерно по окружности с радиусом R, тогда: αr=εR. Нормальное ускорение имеет также связь с угловым: an=ω2R. Учтем это выражение и для полного ускорения получим: a=ar2+an2=Rε2+ω4 Для равнопеременного движения: ω=εt; an=ω2R=ε2t2R и a=Rε2+ε4t4=Rε1+ε2t4.
Практические примеры
Пример 1
На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.
Рисунок 2
Решение
Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки 2.1. и 2.3. показывают направление псевдовектора вверх, а рисунки 2.2. и 2.4. – вниз.
Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки 2.1. и 2.4.). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2. 2. и 2.3.). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
2. и 2.3.). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
Пример 2
Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом R. При этом выражение ϕ=αt3 отражает зависимость угла поворота от времени. Необходимо найти полное ускорение заданной точки как функцию времени.
Решение
Запишем выражения для угловой скорости и углового ускорения заданной точки:
ω=dφdt=3αt2; ε=6αt.
Полное ускорение запишем как:
a=ar2+an2=Rε2+ω4=R36a2t2+81a4t8=3atR4+9a2t6.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор:
Роман Адамчук
Преподаватель физики
10.1 Вращательные переменные | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Описывать физический смысл переменных вращения применительно к вращению с фиксированной осью
- Объясните, как угловая скорость связана с тангенциальной скоростью
- Рассчитать мгновенную угловую скорость с учетом функции углового положения
- Найти угловую скорость и угловое ускорение во вращающейся системе
- Рассчитать среднее угловое ускорение при изменении угловой скорости
- Рассчитать мгновенное угловое ускорение по функции угловой скорости
До сих пор в этом тексте мы в основном изучали поступательное движение, включая описывающие его переменные: смещение, скорость и ускорение. Теперь мы расширим наше описание движения до вращения, точнее, вращательного движения вокруг неподвижной оси. Мы обнаружим, что вращательное движение описывается набором связанных переменных, подобных тем, которые мы использовали в поступательном движении.
Теперь мы расширим наше описание движения до вращения, точнее, вращательного движения вокруг неподвижной оси. Мы обнаружим, что вращательное движение описывается набором связанных переменных, подобных тем, которые мы использовали в поступательном движении.
Угловая скорость
Равномерное круговое движение (обсуждавшееся ранее в разделе Движение в двух и трех измерениях) — это движение по окружности с постоянной скоростью. Хотя это простейший случай вращательного движения, он очень полезен во многих ситуациях, и мы используем его здесь, чтобы ввести вращательные переменные.
На (Рисунок) мы показываем частицу, движущуюся по кругу. Система координат фиксирована и служит в качестве системы отсчета для определения положения частицы. Его вектор положения от начала круга до частицы заметает угол [латекс]\тета[/латекс], который увеличивается в направлении против часовой стрелки по мере того, как частица движется по своей круговой траектории. Угол [латекс]\тета[/латекс] называется угловое положение частицы. Поскольку частица движется по круговой траектории, она также описывает дугу длиной с .
Поскольку частица движется по круговой траектории, она также описывает дугу длиной с .
Рисунок 10.2 Частица движется по круговой траектории. Двигаясь против часовой стрелки, он образует положительный угол [латекс] \тета [/латекс] по отношению к оси x и описывает дугу длиной s.
Угол связан с радиусом окружности и длиной дуги как
[латекс] \theta =\frac{s}{r}. [/latex]
Угол [латекс]\тета[/латекс], угловое положение частицы на ее пути, измеряется в радианах (рад). В [латексе] 360\текст{°} содержится [латекс] 2\пи [/латекс] радиан. [/latex] Обратите внимание, что мера радиана представляет собой отношение измерений длины и, следовательно, является безразмерной величиной. Когда частица движется по круговой траектории, ее угловое положение изменяется, и она испытывает угловые смещения [латекс] \text{Δ}\theta . [/латекс]
Мы можем присвоить векторы величинам на (Рисунок). Угол [латекс] \overset{\to }{\theta} [/латекс] представляет собой вектор вне страницы на (рис. ). Вектор углового положения [latex] \overset{\to }{r} [/latex] и длина дуги [latex] \overset{\to }{s} [/latex] лежат в плоскости страницы. Эти три вектора связаны друг с другом соотношением
). Вектор углового положения [latex] \overset{\to }{r} [/latex] и длина дуги [latex] \overset{\to }{s} [/latex] лежат в плоскости страницы. Эти три вектора связаны друг с другом соотношением
[латекс] \overset{\to }{s}=\overset{\to }{\theta}\,×\,\overset{\to }{r}. [/latex]
То есть длина дуги представляет собой векторное произведение вектора угла и вектора положения, как показано на (рис.).
Рисунок 10.3 Вектор угла указывает вдоль оси z, а вектор положения и вектор длины дуги лежат в плоскости xy. Мы видим, что [латекс] \overset{\to }{s}=\overset{\to }{\theta}\,×\,\overset{\to }{r} [/latex]. Все три вектора перпендикулярны друг другу.
Величина угловой скорости , обозначаемая [латекс] \омега [/латекс], представляет собой скорость изменения угла [латекс] \тета [/латекс] при движении частицы по круговой траектории. мгновенная угловая скорость определяется как предел, в котором [латекс] \текст{Δ}t\до 0 [/латекс] в средней угловой скорости [латекс] \overset{–}{\omega }=\frac{\ text{Δ}\theta}{\text{Δ}t} [/latex]:
[латекс] \omega =\underset{\text{Δ}t\to 0}{\text{lim}}\frac {\text{Δ}\theta}{\text{Δ}t}=\frac{d\theta}{dt}, [/latex]
, где [latex] \theta [/latex] — угол поворота ((Фигура)).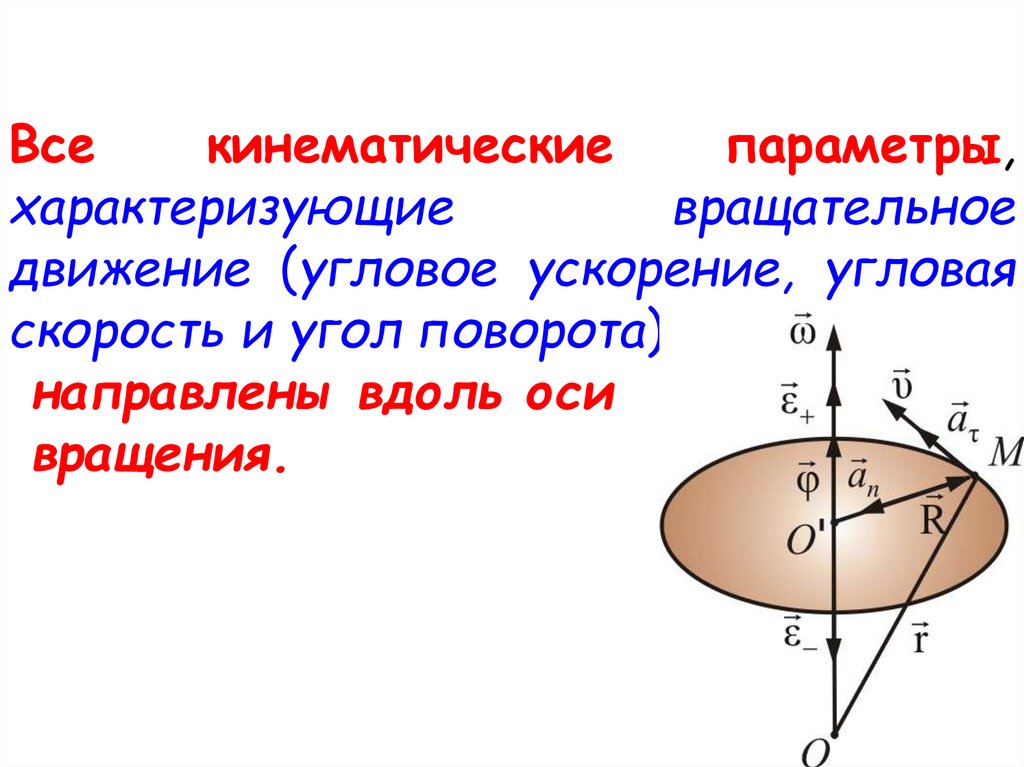 Единицами угловой скорости являются радианы в секунду (рад/с). Угловую скорость также можно назвать скоростью вращения в радианах в секунду. Во многих ситуациях нам дают скорость вращения в оборотах/с или циклах/с. Чтобы найти угловую скорость, мы должны умножить число оборотов/с на [латекс] 2\пи [/латекс], поскольку в одном полном обороте [латекс] 2\пи [/латекс] радиан. Поскольку направление положительного угла в окружности направлено против часовой стрелки, мы принимаем вращение против часовой стрелки как положительное, а вращение по часовой стрелке как отрицательное.
Единицами угловой скорости являются радианы в секунду (рад/с). Угловую скорость также можно назвать скоростью вращения в радианах в секунду. Во многих ситуациях нам дают скорость вращения в оборотах/с или циклах/с. Чтобы найти угловую скорость, мы должны умножить число оборотов/с на [латекс] 2\пи [/латекс], поскольку в одном полном обороте [латекс] 2\пи [/латекс] радиан. Поскольку направление положительного угла в окружности направлено против часовой стрелки, мы принимаем вращение против часовой стрелки как положительное, а вращение по часовой стрелке как отрицательное.
Мы можем увидеть, как угловая скорость связана с тангенциальной скоростью частицы, продифференцировав (рисунок) по времени. Перепишем (Рисунок) как
[латекс] s=r\theta . [/latex]
Взяв производную по времени и учитывая, что радиус r является константой, мы имеем
[латекс] \frac{ds}{dt}=\frac{d}{dt}( r\theta )=\theta \frac{dr}{dt}+r\frac{d\theta}{dt}=r\frac{d\theta}{dt} [/latex]
, где [латекс] \ theta \frac{dr}{dt}=0 [/latex]. Здесь [latex] \frac{ds}{dt} [/latex] просто тангенциальная скорость [латекс] {v}_{\text{t}} [/латекс] частицы на (рис.). Таким образом, используя (Рисунок), мы получаем
Здесь [latex] \frac{ds}{dt} [/latex] просто тангенциальная скорость [латекс] {v}_{\text{t}} [/латекс] частицы на (рис.). Таким образом, используя (Рисунок), мы получаем
[латекс] {v}_{\text{t}}=r\omega . [/latex]
То есть тангенциальная скорость частицы равна ее угловой скорости, умноженной на радиус окружности. Из (рис.) видно, что тангенциальная скорость частицы увеличивается с удалением ее от оси вращения при постоянной угловой скорости. Этот эффект показан на (Рисунок). Две частицы размещены на разных радиусах на вращающемся с постоянной угловой скоростью диске. При вращении диска тангенциальная скорость увеличивается линейно с радиусом от оси вращения. На (рис.) мы видим, что [латекс] {v}_{1}={r}_{1}{\omega }_{1} [/latex] и [латекс] {v}_{2}= {r}_{2}{\omega }_{2} [/latex]. Но диск имеет постоянную угловую скорость, поэтому [латекс] {\ омега } _ {1} = {\ омега } _ {2} [/латекс]. Это означает [латекс] \frac{{v}_{1}}{{r}_{1}}=\frac{{v}_{2}}{{r}_{2}} [/latex] или [латекс] {v}_{2}=(\frac{{r}_{2}}{{r}_{1}}){v}_{1} [/latex]. Таким образом, поскольку [латекс] {r}_{2}>{r}_{1} [/latex], [латекс] {v}_{2}>{v}_{1} [/latex].
Таким образом, поскольку [латекс] {r}_{2}>{r}_{1} [/latex], [латекс] {v}_{2}>{v}_{1} [/latex].
Рисунок 10.4 Две частицы на вращающемся диске имеют разные тангенциальные скорости в зависимости от их расстояния до оси вращения.
До сих пор мы обсуждали величину угловой скорости [латекс] \omega =d\theta \text{/}dt, [/latex], которая является скалярной величиной — изменением углового положения по отношению ко времени . Вектор [латекс] \overset{\to }{\omega} [/латекс] — это вектор, связанный с угловой скоростью и направленный вдоль оси вращения. Это полезно, потому что, когда твердое тело вращается, мы хотим знать как ось вращения, так и направление, в котором тело вращается вокруг оси, по часовой стрелке или против часовой стрелки. Угловая скорость [латекс] \overset{\to }{\omega} [/латекс] дает нам эту информацию. Угловая скорость [латекс] \overset{\to }{\omega} [/латекс] имеет направление, определяемое так называемым правилом правой руки. правило правой руки состоит в том, что если пальцы вашей правой руки вращаются против часовой стрелки от оси x (направление увеличения [латекс]\тета [/латекс]) к оси у-, ваш большой палец указывает в направлении положительной оси z ((Рисунок)). Таким образом, угловая скорость [латекс] \overset{\to }{\omega} [/latex], которая указывает вдоль положительной оси z , соответствует вращению против часовой стрелки, тогда как угловая скорость [латекс] \overset{\to } {\ omega } [/latex], указывающий на минус z — ось соответствует вращению по часовой стрелке.
Таким образом, угловая скорость [латекс] \overset{\to }{\omega} [/latex], которая указывает вдоль положительной оси z , соответствует вращению против часовой стрелки, тогда как угловая скорость [латекс] \overset{\to } {\ omega } [/latex], указывающий на минус z — ось соответствует вращению по часовой стрелке.
Рисунок 10.5 При вращении против часовой стрелки в показанной системе координат угловая скорость указывает в положительном направлении z по правилу правой руки.
Мы можем проверить правило правой руки, используя векторное выражение для длины дуги [латекс] \overset{\to }{s}=\overset{\to }{\theta}\,×\,\overset{ \to}{r}[/latex], (Рисунок). Если мы продифференцируем это уравнение по времени, мы найдем
[латекс] \ frac {d \ overset {\ to {s}} {dt} = \ frac {d} {dt} (\ overset {\ to } {\ theta} \, × \, \ overset {\ to {r}) = (\ frac {d \ overset {\ to } {\ theta}} {dt} \, × \, \ overset {\ to} {r}) + (\ overset {\ to {\ theta} \, × \, \ frac {d \ overset {\ to {r}} {dt}) = \ frac {d \ overset {\ to} {\ theta}} {dt} \, × \, \ overset {\ to} {r}. [/латекс]
[/латекс]
Поскольку [латекс] \overset{\to }{r} [/latex] является константой, член [латекс] \overset{\to }{\theta}\,×\,\frac{d\overset{\ на {r}}{dt}=0 [/latex]. Поскольку [latex] \overset{\to }{v}=\frac{d\overset{\to }{s}}{dt} [/latex] — это тангенциальная скорость, а [latex] \overset{\to }{ \omega }=\frac{d\overset{\to }{\theta}}{dt} [/latex] — угловая скорость, у нас есть
[латекс] \overset{\to }{v}=\overset {\ к } {\ омега} \, × \, \ overset {\ к} {r}. [/latex]
То есть тангенциальная скорость представляет собой векторное произведение угловой скорости и вектора положения, как показано на (рис.). Из части (а) этого рисунка видно, что при угловой скорости в положительных z -направление, вращение в плоскости xy против часовой стрелки. В части (b) угловая скорость находится в отрицательном направлении z-, что дает вращение по часовой стрелке в плоскости xy-.
Рисунок 10.6 Показанные векторы представляют собой угловую скорость, положение и тангенциальную скорость. (a) Угловая скорость указывает в положительном направлении z, что дает вращение против часовой стрелки в плоскости xy. (b) Угловая скорость указывает в отрицательном направлении z, что дает вращение по часовой стрелке.
(a) Угловая скорость указывает в положительном направлении z, что дает вращение против часовой стрелки в плоскости xy. (b) Угловая скорость указывает в отрицательном направлении z, что дает вращение по часовой стрелке.
Пример
Вращение маховика
Маховик вращается так, что образует угол со скоростью [латекс] \theta =\omega t=(45,0\,\text{rad}\text{/}\ text{s)}t [/latex] радианы. Колесо вращается против часовой стрелки, если смотреть в плоскости страницы. а) Чему равна угловая скорость маховика? б) Куда направлена угловая скорость? в) Сколько радиан совершает оборот маховика за 30 с? г) Какова тангенциальная скорость точки маховика на расстоянии 10 см от оси вращения?
Стратегия
Функциональная форма углового положения маховика задается в задаче как [латекс] \тета (t)=\омега t [/латекс], поэтому, взяв производную по времени, мы можем найти угловую скорость. Воспользуемся правилом правой руки, чтобы найти угловую скорость. Чтобы найти угловое смещение маховика за 30 с, мы ищем угловое смещение [латекс] \текст{Δ}\тета [/латекс], где изменение углового положения находится в диапазоне от 0 до 30 с. Чтобы найти тангенциальную скорость точки на расстоянии от оси вращения, мы умножаем ее расстояние на угловую скорость маховика.
Чтобы найти тангенциальную скорость точки на расстоянии от оси вращения, мы умножаем ее расстояние на угловую скорость маховика.
Решение
- [латекс] \omega =\frac{d\theta }{dt}=45\,\text{rad}\text{/}\text{s} [/latex]. Мы видим, что угловая скорость постоянна.
- По правилу правой руки сгибаем пальцы в направлении вращения, то есть против часовой стрелки в плоскости страницы, а большой палец указывает в направлении угловой скорости, которая вне страницы.
- [латекс] \text{Δ}\theta =\theta (30\,\text{s})-\theta (0\,\text{s})=45.0(30.0\,\text{s})- 45,0(0\,\текст{с})=1350,0\,\текст{рад} [/латекс].
- [латекс] {v} _ {\ text {t}} = r \ omega = (0,1 \, \ text {m}) (45,0 \, \ text {rad} \ text{/} \ text {s}) =4,5\,\text{м/с} [/латекс].
Значение
За 30 с маховик сделал довольно много оборотов, около 215, если разделить угловое перемещение на [латекс] 2\пи [/латекс]. Таким образом можно использовать массивный маховик для накопления энергии, если потери на трение минимальны. В недавних исследованиях рассматривались сверхпроводящие подшипники, на которые опирается маховик, с нулевыми потерями энергии из-за трения.
В недавних исследованиях рассматривались сверхпроводящие подшипники, на которые опирается маховик, с нулевыми потерями энергии из-за трения.
Угловое ускорение
Мы только что обсудили угловую скорость для равномерного кругового движения, но не всякое движение является равномерным. Представьте фигуриста, вращающегося с вытянутыми руками — когда он тянет руки внутрь, его угловая скорость увеличивается. Или подумайте о жестком диске компьютера, который останавливается при уменьшении угловой скорости. Мы рассмотрим эти ситуации позже, но мы уже видим необходимость определения углового ускорения для описания ситуаций, когда меняется [латекс] \омега [/латекс]. Чем быстрее меняется [латекс]\омега[/латекс], тем больше угловое ускорение. Мы определяем 9{2} [/латекс].
Таким же образом, как мы определили вектор, связанный с угловой скоростью [латекс] \overset{\to }{\omega} [/latex], мы можем определить [латекс] \overset{\to }{\alpha} [ /латекс], вектор, связанный с угловым ускорением ((Рисунок)). Если угловая скорость направлена вдоль положительной оси z- , как на (рис.), а [латекс] \фрак{д\омега} {dt} [/латекс] положительна, то угловое ускорение [латекс] \оверсет {\to }{\alpha } [/latex] положительно и указывает вдоль оси [latex] +z\text{-} [/latex]. Точно так же, если угловая скорость [латекс] \overset{\to }{\omega} [/латекс] вдоль положительной 9Если ось 0029 z- и [латекс] \frac{d\omega }{dt} [/латекс] отрицательно, то угловое ускорение отрицательно и направлено вдоль оси [латекс] +z- [/латекс].
Если угловая скорость направлена вдоль положительной оси z- , как на (рис.), а [латекс] \фрак{д\омега} {dt} [/латекс] положительна, то угловое ускорение [латекс] \оверсет {\to }{\alpha } [/latex] положительно и указывает вдоль оси [latex] +z\text{-} [/latex]. Точно так же, если угловая скорость [латекс] \overset{\to }{\omega} [/латекс] вдоль положительной 9Если ось 0029 z- и [латекс] \frac{d\omega }{dt} [/латекс] отрицательно, то угловое ускорение отрицательно и направлено вдоль оси [латекс] +z- [/латекс].
Рисунок 10.7 Вращение против часовой стрелки как в (a), так и в (b) с угловой скоростью в том же направлении. (а) Угловое ускорение имеет то же направление, что и угловая скорость, что увеличивает скорость вращения. (b) Угловое ускорение противоположно угловой скорости, что уменьшает скорость вращения.
Вектор тангенциального ускорения можно выразить как векторное произведение углового ускорения и вектора положения. Это выражение можно найти, взяв производную по времени от [латекс] \overset{\to }{v}=\overset{\to }{\omega}\,×\,\overset{\to }{r} [/ латекс] и остается в качестве упражнения:
[латекс] \overset{\to }{\mathbf{\text{a}}}=\overset{\to }{\mathbf{\text{α}}}\ ,×\,\overset{\to }{\mathbf{\text{r}}}.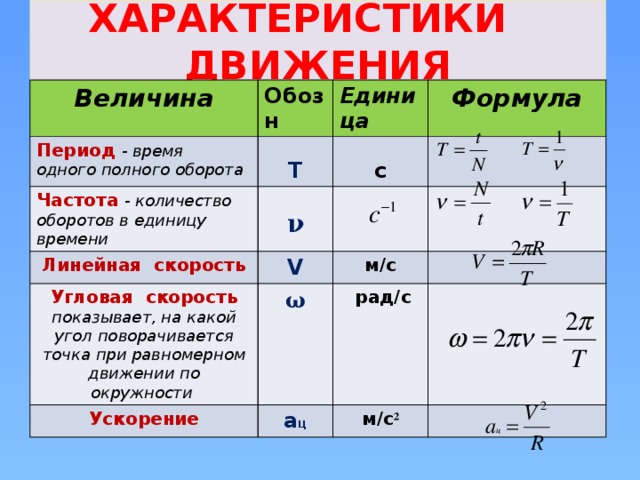 [/latex]
[/latex]
Векторные соотношения для углового ускорения и тангенциального ускорения показаны на (Рисунок).
Рис. 10.8 (a) Угловое ускорение является положительным направлением оси z и вызывает тангенциальное ускорение против часовой стрелки. (b) Угловое ускорение направлено в отрицательном направлении по оси z и создает тангенциальное ускорение по часовой стрелке.
Мы можем связать тангенциальное ускорение точки на вращающемся теле на расстоянии от оси вращения так же, как мы связали тангенциальную скорость с угловой скоростью. Если продифференцировать (рисунок) по времени, учитывая, что радиус r постоянно, получаем
[латекс] {a}_{\text{t}}=r\alpha . [/latex]
Таким образом, тангенциальное ускорение [латекс] {a}_{t} [/латекс] равно произведению радиуса на угловое ускорение. (Рисунок) и (Рисунок) важны для обсуждения качения (см. Угловой момент).
Давайте применим эти идеи к анализу нескольких простых сценариев вращения с фиксированной осью.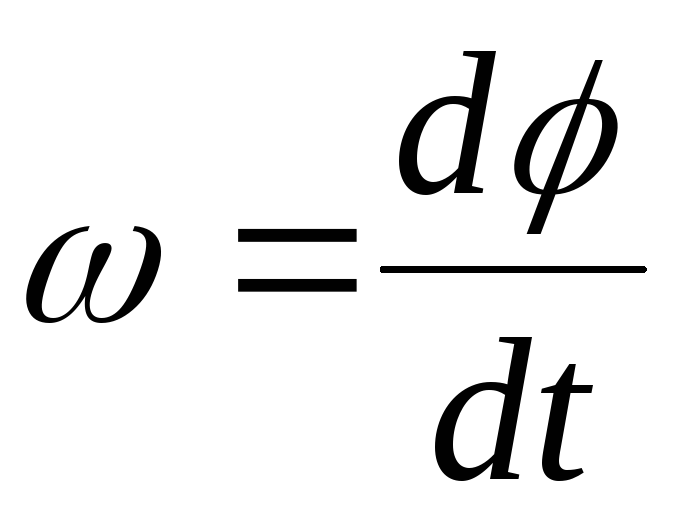 Прежде чем сделать это, мы представляем стратегию решения проблем, которая может быть применена к вращательной кинематике: описание вращательного движения.
Прежде чем сделать это, мы представляем стратегию решения проблем, которая может быть применена к вращательной кинематике: описание вращательного движения.
Стратегия решения проблем: вращательная кинематика
- Изучите ситуацию, чтобы определить, задействована ли вращательная кинематика (вращательное движение).
- Точно определите, что нужно определить в задаче (идентифицируйте неизвестные). Набросок ситуации полезен.
- Составьте полный список того, что дано или может быть выведено из заявленной проблемы (укажите известное).
- Решите соответствующее уравнение или уравнения для определяемой величины (неизвестной). Может быть полезно подумать в терминах поступательного аналога, потому что теперь вы знакомы с уравнениями поступательного движения.
- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численное решение с единицами измерения. Обязательно используйте радианы для углов.
 {2} [/латекс], сколько времени потребуется колесу, чтобы остановиться?
{2} [/латекс], сколько времени потребуется колесу, чтобы остановиться?
Стратегия
Среднее угловое ускорение можно найти непосредственно из его определения [латекс] \overset{–}{\alpha }=\frac{\text{Δ}\omega }{\text{Δ}t} [/ латекс], потому что заданы конечная угловая скорость и время. Мы видим, что [латекс] \text{Δ}\omega ={\omega }_{\text{final}}-{\omega }_{\text{initial}}=250\,\text{об/мин} [/latex] и [latex] \text{Δ}t [/latex] составляет 5,00 с. Для части (b) мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение среднего углового ускорения и решив [латекс] \текст{Δ}t [/латекс], что даст 9{2}}=0,300\,\текст{с}. [/латекс]
Значение
Обратите внимание, что угловое ускорение, когда механик вращает колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю.
Проверьте свои знания
Лопасти вентилятора турбовентиляторного реактивного двигателя (показанного ниже) разгоняются из состояния покоя до скорости вращения 40,0 об/с за 20 с. Увеличение угловой скорости вентилятора постоянно во времени. (GE9ТРДД 0-110В1, установленный на Boeing 777, как показано, в настоящее время является самым большим ТРД в мире, способным развивать тягу 330–510 кН.)
(а) Каково среднее угловое ускорение?
(b) Чему равно мгновенное угловое ускорение в любой момент времени в течение первых 20 с?
Рисунок 10.9 (кредит: «Bubinator»/Wikimedia Commons)
Показать ответ
Пример
Ветряная турбина
Ветряная турбина ((Рисунок)) на ветряной электростанции останавливается на техническое обслуживание. Турбине требуется 30 с, чтобы перейти от рабочей угловой скорости к полной остановке, при которой функция угловой скорости имеет вид [латекс] \omega (t)=[{(t{\text{s}}^{-1} -30.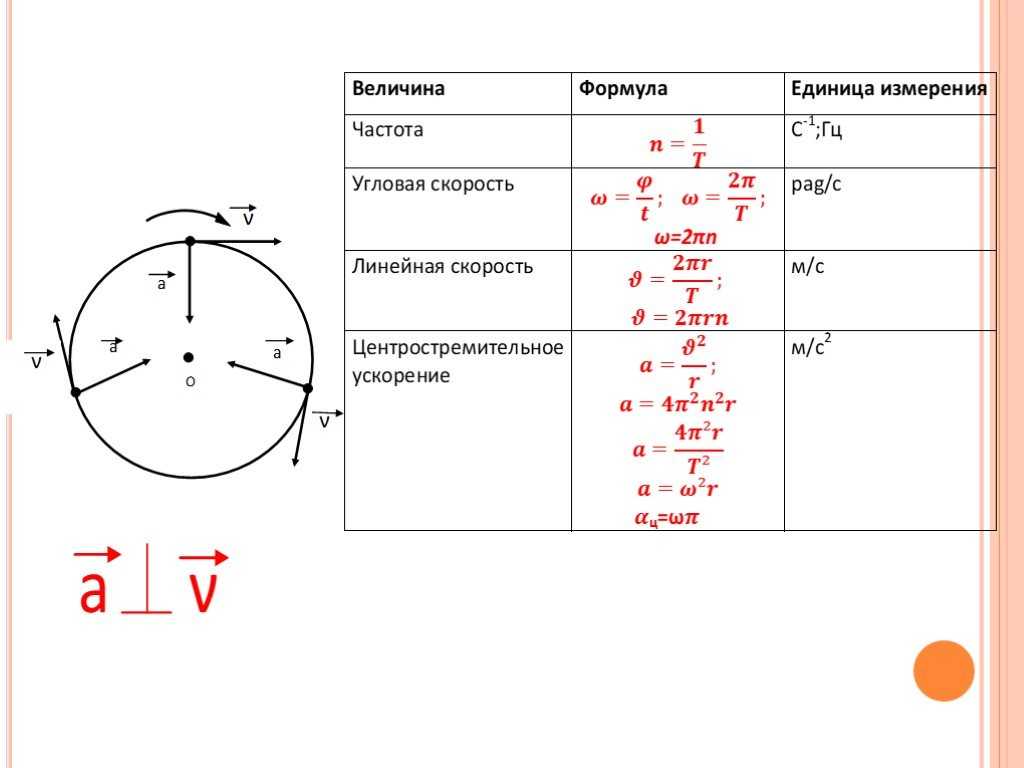 {2}\text{/}100.0]\text{rad}\text{/}\text{s} [/latex]. Если турбина вращается против часовой стрелки, глядя в страницу, а) каковы направления векторов угловой скорости и ускорения? б) Чему равно среднее угловое ускорение? (c) Каково мгновенное угловое ускорение при [латексе] t=0,0,15,0,30,0\,\text{s}? [/латекс]
{2}\text{/}100.0]\text{rad}\text{/}\text{s} [/latex]. Если турбина вращается против часовой стрелки, глядя в страницу, а) каковы направления векторов угловой скорости и ускорения? б) Чему равно среднее угловое ускорение? (c) Каково мгновенное угловое ускорение при [латексе] t=0,0,15,0,30,0\,\text{s}? [/латекс]
Рисунок 10.10 Ветряная турбина, вращающаяся против часовой стрелки, вид сверху.
Стратегия
- Нам дано направление вращения турбины, то есть против часовой стрелки в плоскости страницы. Используя правило правой руки ((Рисунок)), мы можем установить направления векторов угловой скорости и ускорения.
- Рассчитаем начальную и конечную угловые скорости, чтобы получить среднее угловое ускорение. Мы устанавливаем знак углового ускорения из результатов в (а).
- Нам дана функциональная форма угловой скорости, поэтому мы можем найти функциональную форму функции углового ускорения, взяв ее производную по времени.

Решение
- Поскольку турбина вращается против часовой стрелки, угловая скорость [латекс] \overset{\to }{\omega } [/латекс] указывает за пределы страницы. Но поскольку угловая скорость уменьшается, угловое ускорение [латекс] \overset{\to }{\alpha} [/латекс] указывает на страницу в противоположном угловой скорости направлении. 9{2},\,\текст{и}\,\альфа (30,0\,\текст{с})=0\,\текст{рад/с}. [/латекс]
Значение
Из расчетов в (a) и (b) мы обнаружили, что угловое ускорение [латекс] \alpha [/латекс] и среднее угловое ускорение [латекс] \overset{–}{\alpha } [/ латекс] отрицательны. Турбина имеет угловое ускорение, противоположное ее угловой скорости.
Теперь у нас есть базовый словарь для обсуждения кинематики вращения с фиксированной осью и отношений между вращательными переменными. Мы обсудим больше определений и связей в следующем разделе.
Резюме
- Угловое положение [латекс] \тета [/латекс] вращающегося тела — это угол, на который тело повернулось в фиксированной системе координат, которая служит системой отсчета.

- Угловая скорость тела, вращающегося вокруг неподвижной оси, определяется как [латекс] \омега (\текст{рад}\текст{/}\текст{с}) [/латекс], скорость вращения тела в радианах в секунду. Мгновенная угловая скорость вращающегося тела [латекс] \omega =\underset{\text{Δ}t\to 0}{\text{lim}}\frac{\text{Δ}\omega }{\text{Δ }t}=\frac{d\theta }{dt} [/latex] — производная по времени от углового положения [latex] \theta [/latex], найденная путем взятия предела [latex] \text{ Δ}t\to 0 [/latex] в средней угловой скорости [латекс] \overset{–}{\omega }=\frac{\text{Δ}\theta}}{\text{Δ}t} [/latex ]. Угловая скорость связана [латекс] {v}_{\text{t}} [/латекс] с тангенциальной скоростью точки на вращающемся теле через соотношение [латекс] {v}_{\текст{t}} =r\omega[/латекс], где r — радиус до точки, а [latex] {v}_{\text{t}} [/latex] — тангенциальная скорость в данной точке.
- Угловая скорость [латекс] \overset{\to }{\omega } [/латекс] находится по правилу правой руки. Если пальцы скручиваются в направлении вращения вокруг фиксированной оси, большой палец указывает в направлении [латекс] \ перенастройка {\ к {\ омега} [/латекс] (см.
 (Рисунок)).
(Рисунок)).
- Если угловая скорость системы непостоянна, то система имеет угловое ускорение. Среднее угловое ускорение за заданный интервал времени представляет собой изменение угловой скорости за этот интервал времени, [латекс] \overset{–}{\alpha}=\frac{\text{Δ}\omega}{\text{Δ} т} [/латекс]. Мгновенное угловое ускорение представляет собой производную угловой скорости по времени, [латекс] \ альфа = \ недооценка {\ текст {Δ} t \ to 0} {\ текст {lim}} \ гидроразрыва {\ текст {Δ} \ омега} { \text{Δ}t}=\frac{d\omega }{dt} [/latex]. Угловое ускорение [латекс] \overset{\to }{\alpha} [/латекс] находится путем определения угловой скорости. Если скорость вращения вращающегося тела уменьшается, угловое ускорение направлено в сторону, противоположную [латексу] \overset{\to }{\omega} [/латексу]. Если скорость вращения увеличивается, угловое ускорение имеет то же направление, что и [латекс] \overset{\to }{\omega} [/латекс].
- Тангенциальное ускорение точки на радиусе от оси вращения равно произведению углового ускорения на радиус до точки.

Концептуальные вопросы
На стене висят часы. Как вы на это смотрите, как направлен вектор угловой скорости секундной стрелки?
Показать решение
Чему равно угловое ускорение секундной стрелки настенных часов?
Размахивается бейсбольная бита. Все ли точки летучей мыши имеют одинаковую угловую скорость? Та же тангенциальная скорость?
Показать решение
Лопасти блендера на прилавке вращаются по часовой стрелке, если смотреть на него сверху. Если блендер разогнать до большей скорости, в каком направлении будет угловое ускорение лопастей?
Задачи
Вычислите угловую скорость Земли.
Звезда легкой атлетики бежит 400 м по круговой дорожке длиной 400 м за 45 с. Чему равна его угловая скорость, если предположить, что скорость постоянна?
Показать решение
Колесо вращается с постоянной скоростью [латекс] 2,0\,×\,{10}^{3}\,\текст{об}\текст{/}\текст{мин}\, [/латекс]. а) Какова его угловая скорость в радианах в секунду? б) На какой угол он повернется за 10 с? Выразите решение в радианах и градусах.
а) Какова его угловая скорость в радианах в секунду? б) На какой угол он повернется за 10 с? Выразите решение в радианах и градусах.
Частица движется на 3,0 м по окружности радиусом 1,5 м. а) На какой угол он повернется? б) Если частица совершает этот путь за 1,0 с с постоянной скоростью, какова ее угловая скорость? в) Чему равно его ускорение?
Показать решение
Компакт-диск вращается со скоростью 500 об/мин. Если диаметр диска 120 мм, а) какова тангенциальная скорость точки на краю диска? б) В точке на полпути к центру диска?
Необоснованные результаты. 9{2} [/latex] радианы от времени [latex] t=0 [/latex]. На стержне есть две бусины, как показано на следующем рисунке, одна на расстоянии 10 см от оси вращения, а другая — на расстоянии 20 см от оси вращения. а) Какова мгновенная угловая скорость стержня в [латекс] t=5\,\text{s}? [/latex] (b) Каково угловое ускорение стержня? (c) Каковы тангенциальные скорости шариков при [латексе] t=5\,\text{s}? [/latex] (d) Каковы тангенциальные ускорения шариков в [латекс] t=5\,\text{s}? [/latex] (e) Каковы центростремительные ускорения шариков в [латекс] t=5\,\text{s}? [/латекс]
Глоссарий
- угловое ускорение
- временная скорость изменения угловой скорости
- угловое положение
- угол, на который повернулось тело в фиксированной системе координат
- угловая скорость
- временная скорость изменения углового положения
- мгновенное угловое ускорение
- производная угловой скорости по времени
- мгновенная угловая скорость
- производная углового положения по времени
10.
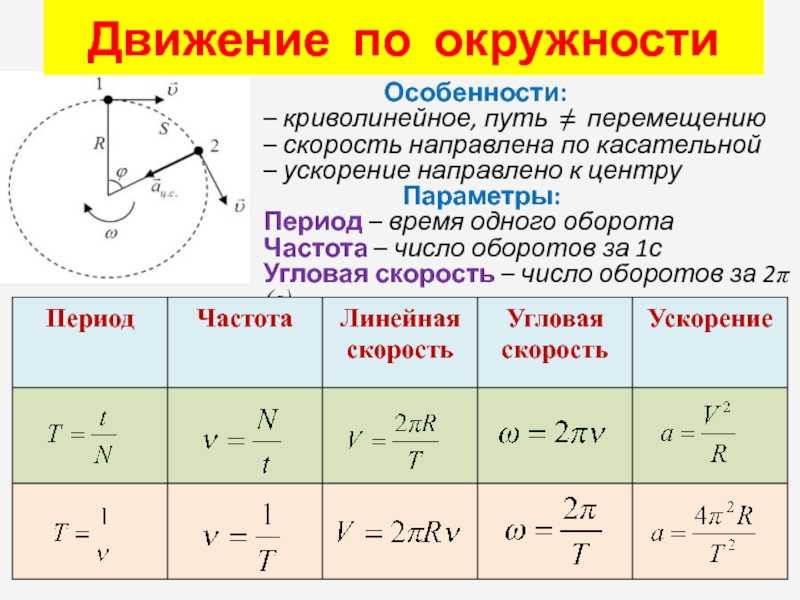 2 Вращение с постоянным угловым ускорением — University Physics Volume 1
2 Вращение с постоянным угловым ускорением — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Вывести кинематические уравнения для вращательного движения с постоянным угловым ускорением
- Выберите из кинематических уравнений для вращательного движения с постоянным угловым ускорением соответствующие уравнения для решения неизвестных при анализе систем, совершающих вращение с неподвижной осью
- Используйте решения, найденные с помощью кинематических уравнений, для проверки графического анализа вращения с фиксированной осью с постоянным угловым ускорением
В предыдущем разделе мы определили вращательные переменные углового смещения, угловой скорости и углового ускорения. В этом разделе мы работаем с этими определениями, чтобы вывести взаимосвязи между этими переменными и использовать эти взаимосвязи для анализа вращательного движения твердого тела вокруг фиксированной оси с постоянным угловым ускорением. Этот анализ формирует основу для кинематики вращения. Если угловое ускорение постоянно, уравнения кинематики вращения упрощаются, подобно уравнениям линейной кинематики, обсуждаемым в «Движении по прямой» и «Движении в двух и трех измерениях». Затем мы можем использовать этот упрощенный набор уравнений для описания многих приложений в физике и технике, где угловое ускорение системы является постоянным. Вращательная кинематика также является предпосылкой для обсуждения вращательной динамики далее в этой главе.
Этот анализ формирует основу для кинематики вращения. Если угловое ускорение постоянно, уравнения кинематики вращения упрощаются, подобно уравнениям линейной кинематики, обсуждаемым в «Движении по прямой» и «Движении в двух и трех измерениях». Затем мы можем использовать этот упрощенный набор уравнений для описания многих приложений в физике и технике, где угловое ускорение системы является постоянным. Вращательная кинематика также является предпосылкой для обсуждения вращательной динамики далее в этой главе.
Кинематика вращательного движения
Используя нашу интуицию, мы можем начать видеть, как величины вращения θ, θ, ω, ω, αα и t связаны друг с другом. Например, в предыдущем разделе мы видели, что если маховик имеет угловое ускорение в том же направлении, что и его вектор угловой скорости, его угловая скорость увеличивается со временем, и его угловое смещение также увеличивается. Наоборот, если угловое ускорение противоположно вектору угловой скорости, его угловая скорость уменьшается со временем.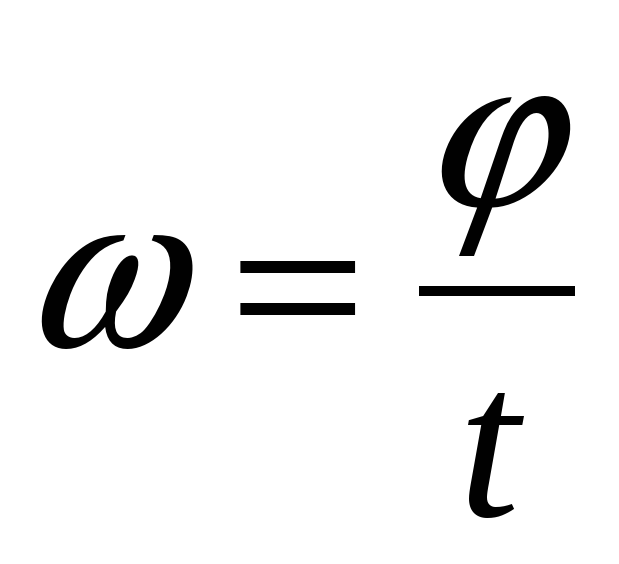 Мы можем описать эти физические ситуации и многие другие с помощью последовательного набора уравнений кинематики вращения при постоянном угловом ускорении. Такой метод исследования вращательного движения называется кинематикой вращательного движения.
Мы можем описать эти физические ситуации и многие другие с помощью последовательного набора уравнений кинематики вращения при постоянном угловом ускорении. Такой метод исследования вращательного движения называется кинематикой вращательного движения.
Для начала отметим, что если система вращается с постоянным ускорением, то средняя угловая скорость подчиняется простому соотношению, поскольку угловая скорость линейно возрастает со временем. Средняя угловая скорость равна половине суммы начального и конечного значений:
ω–=ω0+ωf2.ω–=ω0+ωf2.
10,9
Из определения средней угловой скорости можно найти уравнение, связывающее угловое положение, среднюю угловую скорость и время:
ω–=ΔθΔt.ω–=ΔθΔt.
Решая для θθ, мы имеем
θf=θ0+ω–t, θf=θ0+ω–t,
10,10
, где мы установили t0=0t0=0. Это уравнение может быть очень полезным, если мы знаем среднюю угловую скорость системы. Тогда мы могли бы найти угловое смещение за заданный период времени. Далее находим уравнение, связывающее ωω, αα и t . Чтобы определить это уравнение, начнем с определения углового ускорения:
Тогда мы могли бы найти угловое смещение за заданный период времени. Далее находим уравнение, связывающее ωω, αα и t . Чтобы определить это уравнение, начнем с определения углового ускорения:
α=dωdt.α=dωdt.
Мы преобразуем это, чтобы получить αdt=dωαdt=dω, а затем интегрируем обе части этого уравнения от начальных значений до конечных значений, то есть от t0t0 до t и от ω0 до ωfω0 до ωf. При равномерном вращательном движении угловое ускорение постоянно, поэтому его можно вынести из интеграла, что даст два определенных интеграла:
α∫t0tdt′=∫ω0ωfdω.α∫t0tdt′=∫ω0ωfdω.
Установка t0=0t0=0, имеем
αt=ωf−ω0.αt=ωf−ω0.
Переставляем это, чтобы получить
ωf=ω0+αt,ωf=ω0+αt,
10.11
, где ω0ω0 — начальная угловая скорость. Уравнение 10.11 является вращательным аналогом уравнения линейной кинематики vf=v0+atvf=v0+at. С помощью уравнения 10. 11 мы можем найти угловую скорость объекта в любое заданное время от 90 425 до 90 030, учитывая начальную угловую скорость и угловое ускорение.
11 мы можем найти угловую скорость объекта в любое заданное время от 90 425 до 90 030, учитывая начальную угловую скорость и угловое ускорение.
Теперь проведем аналогичную обработку, начиная с уравнения ω=dθdtω=dθdt. Мы перестраиваем его, чтобы получить ωdt=dθωdt=dθ, и снова интегрируем обе части от начального до конечного значения, отмечая, что угловое ускорение является постоянным и не зависит от времени. Однако на этот раз угловая скорость непостоянна (в общем случае), поэтому подставим в то, что мы вывели выше:
∫t0tf(ω0+αt′)dt′=∫θ0θfdθ;∫t0tω0dt+∫t0tαt′dt′=∫θ0θfdθ=[ω0t′+α((t′)22)]t0t=ω0t+α(t22)=θf− θ0,∫t0tf(ω0+αt′)dt′=∫θ0θfdθ;∫t0tω0dt+∫t0tαt′dt′=∫θ0θfdθ=[ω0t′+α((t′)22)]t0t=ω0t+α(t22)=θf −θ0,
, где мы установили t0=0t0=0. Теперь переставляем, чтобы получить
θf=θ0+ω0t+12αt2.θf=θ0+ω0t+12αt2.
10.12
Уравнение 10.12 представляет собой вращательный аналог уравнения линейной кинематики, найденного в книге «Движение вдоль прямой линии» для положения как функции времени.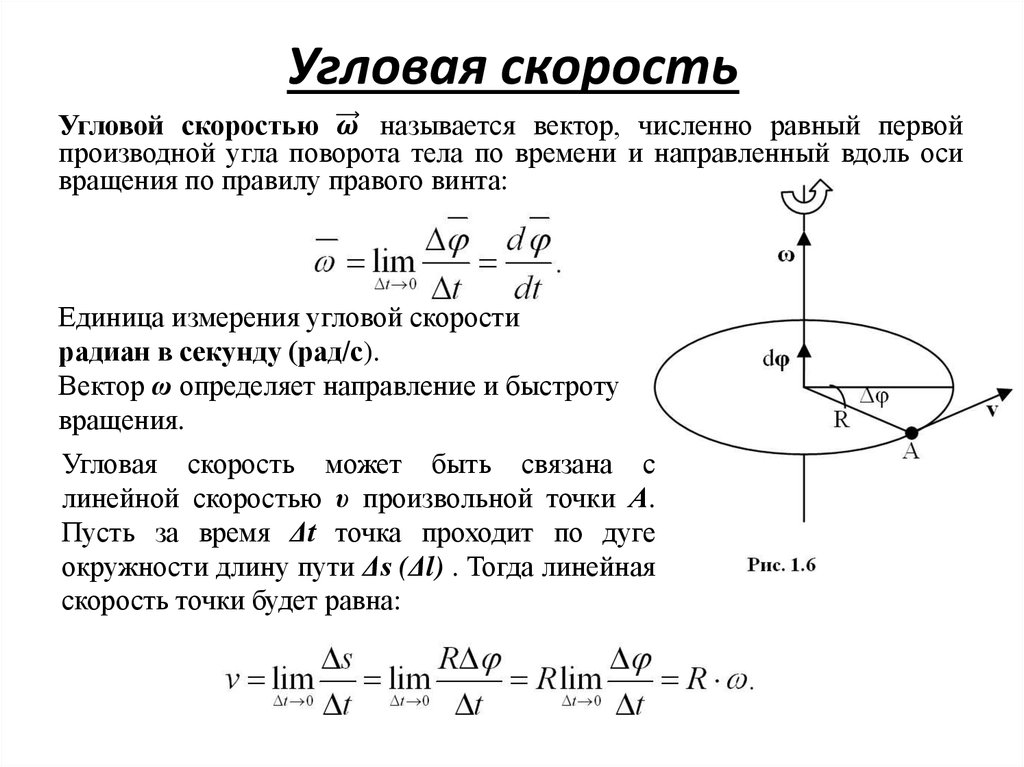 Это уравнение дает нам угловое положение вращающегося твердого тела в любой момент времени t заданы начальные условия (начальное угловое положение и начальная угловая скорость) и угловое ускорение.
Это уравнение дает нам угловое положение вращающегося твердого тела в любой момент времени t заданы начальные условия (начальное угловое положение и начальная угловая скорость) и угловое ускорение.
Мы можем найти уравнение, которое не зависит от времени, решив для t в уравнении 10.11 и подставив в уравнение 10.12. Уравнение 10.12 становится
?0005
или
ωf2=ω02+2α(Δθ).ωf2=ω02+2α(Δθ).
10.13
Уравнения с 10.10 по 10.13 описывают вращение с фиксированной осью для постоянного ускорения и сведены в Таблицу 10.1.
| Угловое смещение от средней угловой скорости | θf=θ0+ω–tθf=θ0+ω–t |
| Угловая скорость из углового ускорения | ωf=ω0+αtωf=ω0+αt |
| Угловое смещение от угловой скорости и углового ускорения | θf=θ0+ω0t+12αt2θf=θ0+ω0t+12αt2 |
| Угловая скорость по угловому смещению и угловому ускорению | ωf2=ω02+2α(Δθ)ωf2=ω02+2α(Δθ) |
Стол
10. 1
1
Кинематические уравнения
Применение уравнений вращательного движения
Теперь мы можем применить ключевые кинематические соотношения для вращательного движения к нескольким простым примерам, чтобы понять, как уравнения можно применять в повседневных ситуациях.
Пример
10.4
Расчет ускорения рыболовной катушки
Глубоководный рыбак ловит на крючок большую рыбу, которая уплывает от лодки, вытягивая леску из своей рыболовной катушки. Вся система изначально находится в покое, а леска разматывается с катушки на радиусе 4,50 см от ее оси вращения. Катушке придается угловое ускорение 110 рад/с2110 рад/с2 в течение 2,00 с (рис. 10.11).
а) Какова конечная угловая скорость барабана через 2 с?
(б) Сколько оборотов делает катушка?
Рисунок
10.11
Леска, сходящая с вращающейся катушки, движется линейно.
Стратегия
Определите известные и сравните с кинематическими уравнениями для постоянного ускорения. Найдите подходящее уравнение, которое можно решить относительно неизвестного, используя известные в описании задачи.
Найдите подходящее уравнение, которое можно решить относительно неизвестного, используя известные в описании задачи.
Решение
- Нам даны αα и t , и мы хотим определить ωω. Наиболее просто использовать уравнение ωf=ω0+αtωf=ω0+αt, поскольку известны все члены, кроме неизвестной переменной, которую мы ищем. Нам дано, что ω0=0ω0=0 (начинается из состояния покоя), поэтому
ωf=0+(110рад/с2)(2,00с)=220рад/с.ωf=0+(110рад/с2)(2,00с)=220рад/с.
- Нас просят найти количество оборотов. Поскольку 1 об = 2 π рад 1 об = 2 π рад, мы можем найти количество оборотов, найдя θθ в радианах. Нам даны αα и t , и мы знаем, что ω0ω0 равно нулю, поэтому мы можем получить θθ, используя
θf=θi+ωit+12αt2=0+0+(0,500)(110рад/с2)(2,00с)2=220рад.θf=θi+ωit+12αt2=0+0+(0,500)(110рад/с2)( 2.00с)2=220рад.
Преобразование радианов в обороты дает
Число оборотов=(220рад)1об2πрад=35.
 0об. Число оборотов=(220рад)1об2πрад=35.0об.
0об. Число оборотов=(220рад)1об2πрад=35.0об.
Значение
Этот пример показывает, что отношения между величинами вращения во многом аналогичны отношениям между линейными величинами. Ответы на вопросы реалистичны. После размотки в течение двух секунд обнаруживается, что катушка вращается со скоростью 220 рад/с, что составляет 2100 об/мин. (Неудивительно, что барабаны иногда издают высокие звуки.)
В предыдущем примере мы рассмотрели рыболовную катушку с положительным угловым ускорением. Теперь рассмотрим, что происходит при отрицательном угловом ускорении.
Пример
10,5
Расчет продолжительности замедления и остановки рыболовной катушки
Теперь рыбак тормозит спиннинговую катушку, достигая углового ускорения -300рад/с2-300рад/с2. Сколько времени требуется барабану, чтобы остановиться?
Стратегия
Нас просят найти время t , чтобы барабан остановился. Начальные и конечные условия отличаются от условий в предыдущей задаче, в которой использовалась та же рыболовная катушка. Теперь мы видим, что начальная угловая скорость ω0=220рад/sω0=220рад/с, а конечная угловая скорость ωω равна нулю. Угловое ускорение задается как α=-300 рад/с2.α=-300рад/с2. Исследуя имеющиеся уравнения, мы видим все величины, кроме t известны в ωf=ω0+αtωf=ω0+αt, что упрощает использование этого уравнения.
Начальные и конечные условия отличаются от условий в предыдущей задаче, в которой использовалась та же рыболовная катушка. Теперь мы видим, что начальная угловая скорость ω0=220рад/sω0=220рад/с, а конечная угловая скорость ωω равна нулю. Угловое ускорение задается как α=-300 рад/с2.α=-300рад/с2. Исследуя имеющиеся уравнения, мы видим все величины, кроме t известны в ωf=ω0+αtωf=ω0+αt, что упрощает использование этого уравнения.
Раствор
Уравнение утверждает
ωf=ω0+αt.ωf=ω0+αt.
Алгебраически решаем уравнение для t и затем, как обычно, подставляем известные значения, что дает 220,0 рад/с−300,0 рад/с2=0,733 с.
Значение
Обратите внимание, что необходимо соблюдать осторожность со знаками, указывающими направления различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда рвется из-за связанных с ней ускорений, и рыбаки часто позволяют рыбе немного поплавать, прежде чем затормозить катушку. Уставшая рыба медленнее, и ей требуется меньшее ускорение.
Леска иногда рвется из-за связанных с ней ускорений, и рыбаки часто позволяют рыбе немного поплавать, прежде чем затормозить катушку. Уставшая рыба медленнее, и ей требуется меньшее ускорение.
Проверьте свое понимание
10.2
Центрифуга, используемая для выделения ДНК, вращается с максимальной скоростью 7000 об/мин, создавая на образце «перегрузку», которая в 6000 раз превышает силу тяжести. Если центрифуге требуется 10 секунд, чтобы прийти в состояние покоя с максимальной скорости вращения: (a) Каково угловое ускорение центрифуги? б) Каково угловое перемещение центрифуги за это время?
Пример
10,6
Угловое ускорение воздушного винта
На рис. 10.12 показан график зависимости угловой скорости воздушного винта самолета от времени. Его угловая скорость начинается с 30 рад/с и линейно падает до 0 рад/с в течение 5 секунд. а) Найдите угловое ускорение объекта и проверьте результат с помощью кинематических уравнений. (b) Найдите угол, на который поворачивается пропеллер за эти 5 секунд, и проверьте свой результат, используя уравнения кинематики.
(b) Найдите угол, на который поворачивается пропеллер за эти 5 секунд, и проверьте свой результат, используя уравнения кинематики.
Рисунок
10.12
График зависимости угловой скорости винта от времени.
Стратегия
- Поскольку угловая скорость изменяется линейно со временем, мы знаем, что угловое ускорение постоянно и не зависит от временной переменной. Угловое ускорение представляет собой наклон графика зависимости угловой скорости от времени, α=dωdtα=dωdt. Чтобы рассчитать наклон, мы читаем непосредственно из рисунка 10.12 и видим, что ω0=30рад/sω0=30рад/с при t=0st=0с и ωf=0рад/sωf=0рад/с при t=5st=5с. Затем мы можем проверить результат, используя ω=ω0+αtω=ω0+αt.
- Используем уравнение ω=dθdt;ω=dθdt; поскольку производная угла по времени является угловой скоростью, мы можем найти угловое смещение, интегрируя угловую скорость, что на рисунке означает взятие площади под графиком угловой скорости. Другими словами:
∫θ0θfdθ=θf−θ0=∫t0tfω(t)dt.
 ∫θ0θfdθ=θf−θ0=∫t0tfω(t)dt.
∫θ0θfdθ=θf−θ0=∫t0tfω(t)dt.Затем мы используем кинематические уравнения для постоянного ускорения, чтобы проверить результат.
Решение
- Вычисляя наклон, получаем
α=ω−ω0t−t0=(0−30,0)рад/с(5,0−0)s=−6,0рад/с2.α=ω−ω0t−t0=(0−30,0)рад/с(5,0−0) )s=−6,0 рад/с2.
Мы видим, что это точно такое же уравнение 10.11 с небольшой перестановкой членов.
- Мы можем найти площадь под кривой, вычислив площадь прямоугольного треугольника, как показано на рис. 10.13.
Рисунок
10.13Площадь под кривой – это площадь прямоугольного треугольника.
Δθ=площадь(треугольник);Δθ=12(30рад/с)(5с)=75рад.Δθ=площадь(треугольник);Δθ=12(30рад/с)(5с)=75рад.
Мы проверяем решение, используя уравнение 10.12:
θf=θ0+ω0t+12αt2.θf=θ0+ω0t+12αt2.
Полагая θ0=0θ0=0, имеем
θf=(30,0рад/с)(5,0с)+12(−6,0рад/с2)(5,0рад/с)2=150,0−75,0=75,0рад.θf=(30,0рад/с)(5,0с)+ 12(−6,0рад/с2)(5,0рад/с)2=150,0−75,0=75,0рад.
Это подтверждает решение, найденное путем нахождения площади под кривой.

 {2} [/латекс], сколько времени потребуется колесу, чтобы остановиться?
{2} [/латекс], сколько времени потребуется колесу, чтобы остановиться?


 0об. Число оборотов=(220рад)1об2πрад=35.0об.
0об. Число оборотов=(220рад)1об2πрад=35.0об. ∫θ0θfdθ=θf−θ0=∫t0tfω(t)dt.
∫θ0θfdθ=θf−θ0=∫t0tfω(t)dt.