Содержание
Равномерное движение по окружности 11 класс онлайн-подготовка на Ростелеком Лицей
Величины, входящие в уравнения кинематики равномерного движения по окружности
В уравнения кинематики равномерного движения по окружности входят следующие понятия:
1. T (период) – время одного полного оборота.
2. – частота обращения.
Частота и период – обратно пропорциональные величины:
3. R – радиус окружности, по которому движется тело
4. – линейная скорость (скорость вдоль траектории). Так как за время, равное периоду, тело проходит путь, равный длине окружности, то:
5. – угловая скорость. Она равна отношению угла поворота за все время периода ко времени одного полного оборота.
Линейная скорость связана с угловой следующим соотношением:
6. Если происходит равномерное движение по окружности, то это не означает, что оно не имеет ускорения. Скорость по величине не меняется, но по направлению скорость меняется все время. Поэтому нормальное ускорение, которое характеризует быстроту изменения направления скорости, в данном случае называется центростремительным (направлено к центру окружности) и вычисляется по следующим формулам:
Поэтому нормальное ускорение, которое характеризует быстроту изменения направления скорости, в данном случае называется центростремительным (направлено к центру окружности) и вычисляется по следующим формулам:
Задача 1 (определение линейной скорости)
Найти линейную скорость точки при движении по окружности радиусом 1 м при угловой скорости . Варианты ответа: 1. ; 2. ; 3. ; 4. .
Дано: ;
Найти:
Решение
Линейная скорость находится по следующей формуле:
Ответ: 3. .
Задача 2 (определение периода вращения)
Найти период вращения вала при частоте 60 оборотов в минуту. Варианты ответа: 1. ; 2. ; 3. ; 4. .
Дано:
Найти:
Решение
Частота равна 60 оборотов в минуту, а минута – это 60 секунд, следовательно, за 60 секунд выполняется 60 оборотов, а за одну секунду выполняется один оборот. Одна секунда и есть искомый период вращения.
Одна секунда и есть искомый период вращения.
Ответ: 3. .
Задача 3 (определение отношения линейных скоростей)
Длина минутной стрелки часов в 1,5 раза больше длины часовой стрелки. Во сколько раз скорость конца минутной стрелки больше скорости конца часовой? Варианты ответа: 1. 12; 2. 18; 3. 24; 4. 36.
Дано: ;
Найти:
Решение
Скорость при движении по окружности вычисляется по формуле:
Следовательно:
Ответ: 2. 18.
Задача 4 (определение радиуса)
Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 4 раза больше линейной скорости точки, лежащей на 0,9 м ближе к оси колеса.
Дано: ; (см. Рис. 1)
Найти: R
Решение
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображено колесо. Точка A лежит на ободе, точка B ближе к оси колеса на
Точка A лежит на ободе, точка B ближе к оси колеса на
При вращении колеса общей кинематической величиной для всех точек является угловая скорость (все точки двигаются с одной и той же угловой скоростью).
Следовательно, линейная скорость точки A равна:
Линейная скорость точки B равна:
Поэтому, если:
то:
Ответ: .
Задача 5 (определение линейной скорости и центростремительного ускорения)
Найти скорость и ускорение Исаакиевского собора, обусловленные вращением Земли.
Дано: – радиус Земли; Исаакиевский собор находится в Санкт-Петербурге, который находится на северной широты ; – время обращения Земли вокруг своей оси (см. Рис. 2).
Найти: ;
Решение
Рис. 2. Иллюстрация к задаче
Исаакиевский собор вместе с Землей совершает движение по окружности, радиус которой равен:
Следовательно, скорость Исаакиевского собора будет равна отношению длины этой окружности к периоду:
Подставим в это выражение известные значения:
Центростремительное ускорение вычисляется по формуле:
Подставим в это выражение известные значения:
Ответ: ; .
Список литературы
- Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А. П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- О. Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А. В. Перышкин, В. В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
- Орлов В. А., Демидова М. Ю., Никифоров Г. Г., Ханнанов Н. К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «eduspb.com» (Источник)
- Интернет-портал «abramova.vitut.ru» (Источник)
- Интернет-портал «bambookes.ru» (Источник)
Домашнее задание
- Упражнение 5 (1,2) стр. 52 – Г. Я.
 Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10 (см. список рекомендованной литературы).
Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10 (см. список рекомендованной литературы). - Автомобиль движется по дороге со скоростью 72 км/час. Определите, с какой скоростью относительно Земли движется ось его колеса, его нижняя и верхняя точки.
- Период вращения лопастей ветряной мельницы равен 5 с. Определите число оборотов лопастей за 1 ч.
- ньютоновская механика
- Задайте длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Рассчитайте угловую скорость вращения колеса автомобиля.
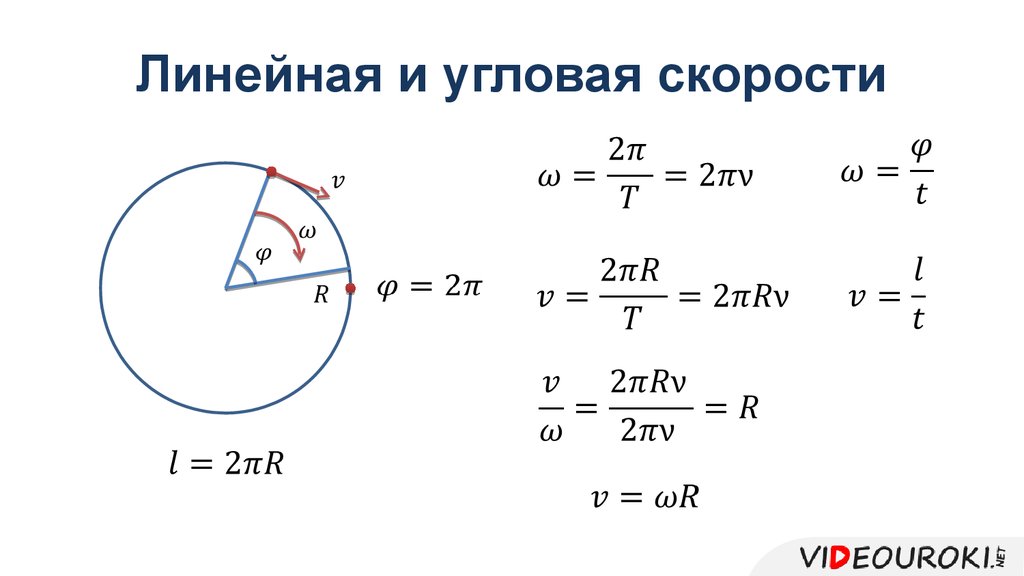
- Равномерное круговое движение – это движение по окружности с постоянной скоростью. Угол поворота определяется как отношение длины дуги к радиусу кривизны:
, где длина дуги — это расстояние, пройденное по круговому пути, и радиус кривизны кругового пути.

Угловая скорость
1. 54 Найти угловую скорость вращения электрона вокруг ядра
В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость ω вращения электрона вокруг ядра и его нормальное ускорение аn.
1. 55 Найти для точек на ободе колеса угловую скорость
Колесо радиусом R = 10 см вращается с угловым ускорением ε = 3,14 рад/с2.
1. 60 Найти через время после начала движения угловую скорость
Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ=А+B+Ct2, где В = 2 рад/с и С = 1 рад/с3.
1. 41 Найти угловую скоростью суточного вращения Земли
Найти угловую скоростью ω: а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин.
1. 46 Найти угловое ускорение колеса
Колесо, вращаясь равноускоренно, достигло угловой скорости ω = 20 рад/с через N = 10 об после начала вращения. Найти угловое ускорение ε колеса.
469 Определить максимальную мощность необходимую для вращения…
Проволочный контур площадью \(S = 500\) см2 и сопротивлением \(R = 0,1\) Ом равномерно вращается в однородном магнитном поле (\(B = 0,5\) Тл). Ось вращения лежит в плоскости кольца и перпендикулярна линиям магнитной индукции.
422 Определить магнитный момент при вращении диска…
Диск радиусом \(R = 8\) см несет равномерно распределенный по поверхности заряд (\(\sigma = 100\) нКл/м2). Определить магнитный момент \({P_m}\), обусловленный вращением диска, относительно оси, проходящей через его центр и перпендикулярной плоскости диска.
Определить магнитный момент \({P_m}\), обусловленный вращением диска, относительно оси, проходящей через его центр и перпендикулярной плоскости диска.
425 Найти магнитный момент обусловленный вращением…
Тонкое кольцо радиусом \(R = 10\) см несет равномерно распределенный заряд \(Q = 80\) нКл. Кольцо вращается с угловой скоростью \(\omega = 50\) рад/с относительно оси, совпадающей с одним из диаметров кольца. Найти магнитный момент \({P_m}\), обусловленный вращением кольца.
426 Найти магнитный момент обусловленный вращением стержня…
Заряд \(Q = 0,1\) мкКл равномерно распределен по стержню длиной \(L = 50\) см. Стержень вращается с угловой скоростью \(\omega = 20\) рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Найти магнитный момент \({P_m}\), обусловленный вращением стержня.
429 Определить магнитный момент P…
По поверхности диска радиусом \(R = 15\) см равномерно распределен заряд \(Q = 0,2\) мкКл. Диск вращается с угловой скоростью \(\omega = 30\) рад/с относительно оси, перпендикулярной плоскости диска и проходящей через его центр.
152 С какой угловой скоростью будет вращаться скамья…
На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω = 4 рад/с.
153 С какой угловой скоростью будет вращаться платформа…
Платформа в виде диска диаметром D = 3 м и массой m1 = 180 кг может вращаться вокруг вертикальной оси.
155 С какой скоростью станет вращаться скамья…
На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω = 25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского.
158 С какой угловой скоростью начнет вращаться скамья…
На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой m1 = 6 кг стоит человек массой m2 = 60 кг.
159 С какой угловой скоростью начнет вращаться платформа. ..
..
Горизонтальная платформа массой M = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой ν2 = 8 мин-1. Человек массой m = 70 кг стоит при этом на краю платформы.
168 Определить линейную и угловую скорости спутника…
Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте r = 1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус Rз считать известными.
107 Во сколько раз путь будет больше модуля перемещения…
Материальная точка движется по окружности с постоянной угловой скоростью ω = π/6 рад/с. Во сколько раз путь ΔS, пройденный точкой за время T = 4 с, будет больше модуля ее перемещения Δr ?
109 Каково наибольшее ускорение движения человека…
По краю равномерно вращающейся с угловой скоростью ω = 1 рад/с платформы идет человек и обходит платформу за время t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
143 Определить момент инерции маховика…
На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг.
ньютоновская механика — Определение угловой скорости по тангенциальной скорости и радиусу
спросил
Изменено
4 года, 3 месяца назад
Просмотрено
305 раз
$\begingroup$
У меня в голове не укладывается проблема, которую я пытаюсь решить. Мне даны тангенциальные скорости двух объектов, совершающих равномерное круговое движение, и разница их радиусов, и я должен каким-то образом найти угловую скорость. Задача примерно такая: две машины движутся по двум разным гоночным трассам. Радиус колеи для вагона 2 равен 0,9.умножить на радиус пути для автомобиля 1. Обе машины стартуют рядом, вдоль радиальной линии, и движутся с одинаковой скоростью против часовой стрелки. Сколько оборотов сделал автомобиль 2, когда скорости автомобиля 1 и автомобиля 2 в первый раз направлены в противоположные стороны.
Задача примерно такая: две машины движутся по двум разным гоночным трассам. Радиус колеи для вагона 2 равен 0,9.умножить на радиус пути для автомобиля 1. Обе машины стартуют рядом, вдоль радиальной линии, и движутся с одинаковой скоростью против часовой стрелки. Сколько оборотов сделал автомобиль 2, когда скорости автомобиля 1 и автомобиля 2 в первый раз направлены в противоположные стороны.
Будем признательны за любую помощь…
$\endgroup$
$\begingroup$
Сначала вспомним, что скорость определяется выражением
$$v(t)=\frac{dl}{dt}$$
а в случае кругового движения $l=r\\theta$, поэтому $v=r\frac{d\theta}{dt}$. Теперь вспомним, что $\frac{d\theta}{dt}=\omega$. Затем находим $\omega=v/r$.
Теперь, что касается машины, мы знаем, что $v$ одинакова для обеих машин. Пусть автомобиль 1 находится в радиусе $R$ . Тогда его угловая скорость будет $\omega_1=v/R$. С другой стороны, автомобиль 2 будет иметь угловую скорость $\omega_2=v/0.9R$. Теперь мы знаем угловые скорости обоих автомобилей.
С другой стороны, автомобиль 2 будет иметь угловую скорость $\omega_2=v/0.9R$. Теперь мы знаем угловые скорости обоих автомобилей.
Осталось выяснить, когда их скорости будут направлены в противоположные стороны. Должно быть очевидно, что это происходит, когда две машины находятся на противоположных концах круга. В частности, нам понадобится $$\theta_2(t)-\theta_1(t)=\pi$$
Затем пишем:
$$\omega_2t-\omega_1t=\frac{v}{R}(1-0,9)t=0,1\frac{v}{R}t=\pi$$
поэтому время, в которое это происходит, равно $t_0=10\pi R/v$.
Наконец, чтобы найти угловое расстояние, которое проедет автомобиль 2, мы возьмем $R\omega_2t_0$ и получим, что оно равно $9\pi R$. Это равно 4,5 окружности окружности, поэтому вторая машина совершит $\mathbf{4,5\ оборота}$ к тому моменту, когда они будут иметь противоположные скорости.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
6.1 Угол вращения и угловая скорость – Колледж физики
Резюме
В главе 2 «Кинематика» мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. В главе 3 «Двумерная кинематика» речь шла о движении в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Когда объекты вращаются вокруг некоторой оси — например, когда CD (компакт-диск) на рис. 1 вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Мы определяем угол поворота как отношение длины дуги к радиусу кривизны:
1 вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Мы определяем угол поворота как отношение длины дуги к радиусу кривизны:
Рисунок 1. Все точки на компакт-диске движутся по дугам окружности. Ямы вдоль линии от центра к краю все перемещаются на один и тот же угол Δ θ за время Δ t . Рис. 2. Радиус окружности повернут на угол Δ θ . Длина дуги Δ с описана на окружности.
Длина дуги — это расстояние, пройденное по круговой траектории, как показано на рисунке 2. Обратите внимание, что радиус кривизны кругового пути.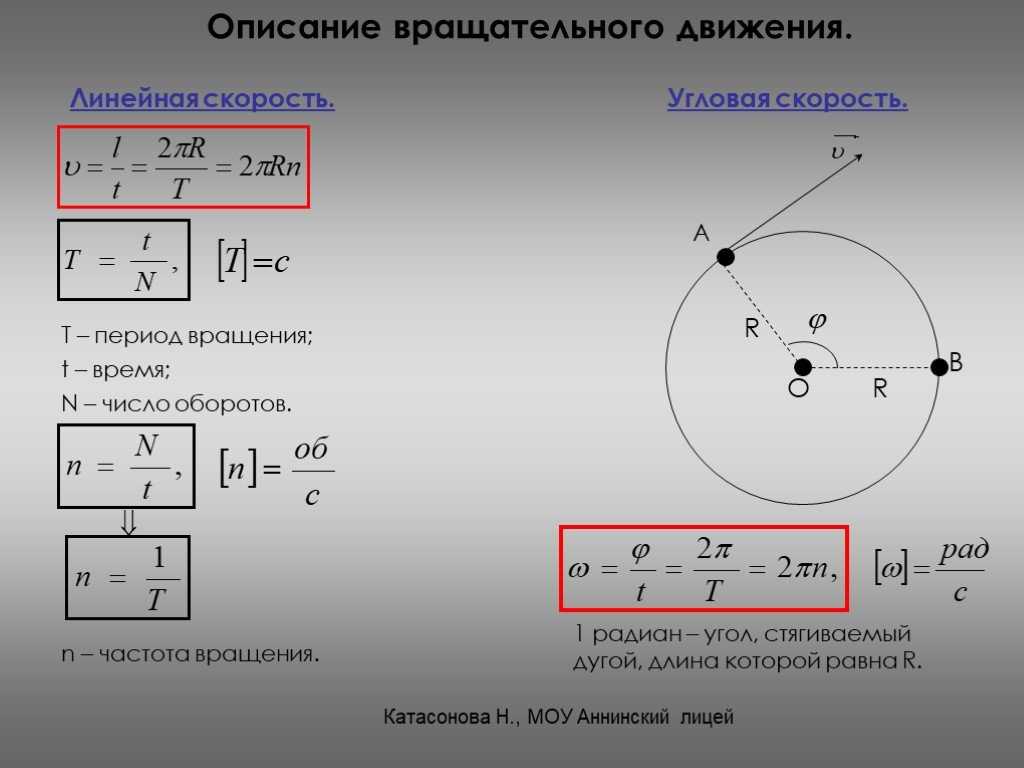
Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса Окружность окружности равна Таким образом, для одного полного оборота угол поворота равен
Этот результат является основой для определения единиц, используемых для измерения углов поворота, равных радиан (рад), определенных таким образом, что
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.
| Таблица 1. Сравнение угловых единиц. | |
Рис. 3. Точки 1 и 2 поворачиваются на один и тот же угол (Δ θ ) , но точка 2 движется по большей дуге (Δ s ) , потому что она находится на большем расстоянии от центра вращения ( r ) .
3. Точки 1 и 2 поворачиваются на один и тот же угол (Δ θ ) , но точка 2 движется по большей дуге (Δ s ) , потому что она находится на большем расстоянии от центра вращения ( r ) .
Если тогда компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге есть один оборот, отношение между радианами и градусами, таким образом, равно
.
так что
Как быстро вращается объект? Мы определяем угловая скорость как скорость изменения угла. В символах это
где угловой поворот происходит за время Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость аналогична линейной скорости Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается на длину дуги за время и поэтому имеет линейную скорость
Эта яма перемещается на длину дуги за время и поэтому имеет линейную скорость
Отсюда мы видим, что подставляя это в выражение для дает
Мы записываем это отношение двумя разными способами и получаем два разных понимания:
Первое соотношение в утверждает, что линейная скорость пропорциональна расстоянию от центра вращения, поэтому она наибольшая для точки на ободе (наибольшая), как и следовало ожидать. Мы также можем назвать эту линейную скорость точки на ободе тангенциальной скоростью . Второе соотношение можно проиллюстрировать, рассмотрев шину движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости автомобиля. См. рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большое значение означает большое, поскольку аналогично, шина большего радиуса, вращающаяся с той же угловой скоростью ( ), создает большую линейную скорость ( ) для автомобиля.
Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω . Скорость протектора шины относительно оси v , такая же, как если бы автомобиль был поднят на домкрат. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω , где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Скорость протектора шины относительно оси v , такая же, как если бы автомобиль был поднят на домкрат. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω , где r — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля.
Пример 1: Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью (около ). См. рис. 4.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, радиус шины принимается равным Зная, и мы можем использовать второе соотношение для рассчитать угловую скорость.
Решение
Для расчета угловой скорости воспользуемся следующим соотношением:
Подстановка известных,
Обсуждение
Когда мы исключаем единицы измерения в приведенном выше расчете, мы получаем 50,0/с. Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояния), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость
Но угловая скорость должна иметь единицы рад/с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояния), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землеройная машина с гораздо большими шинами, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, ее шины вращались бы медленнее. Они будут иметь угловую скорость
Оба и имеют направления (следовательно, они угловая и линейная скорости , соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на рисунке 5.
ВОЗМОЖНЫЙ ЭКСПЕРИМЕНТ
Привяжите какой-либо предмет к концу веревки и раскачайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке.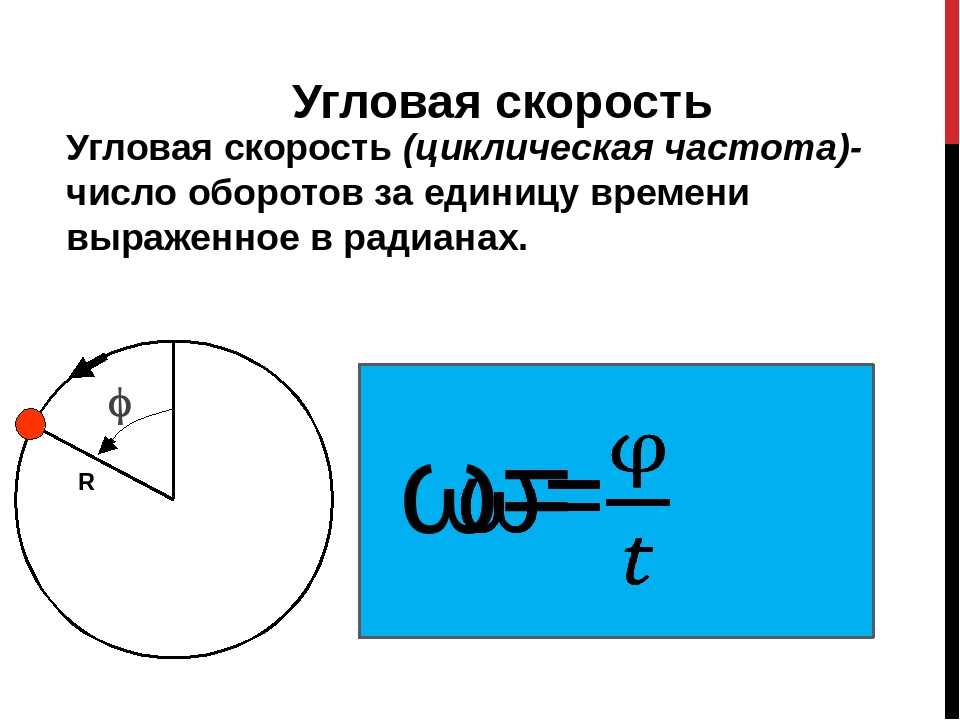 Определите другие круговые движения и измерьте их угловые скорости.
Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5. Поскольку объект движется по кругу, в данном случае муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.
ИССЛЕДОВАНИЯ PHET: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ
Рис. 6. Революция божьей коровки
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.
 Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10 (см. список рекомендованной литературы).
Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика 10 (см. список рекомендованной литературы).