Что такое угловая скорость и как ее рассчитывают?

Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а угловая скорость. Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.

Угловая скорость: понятие и формула

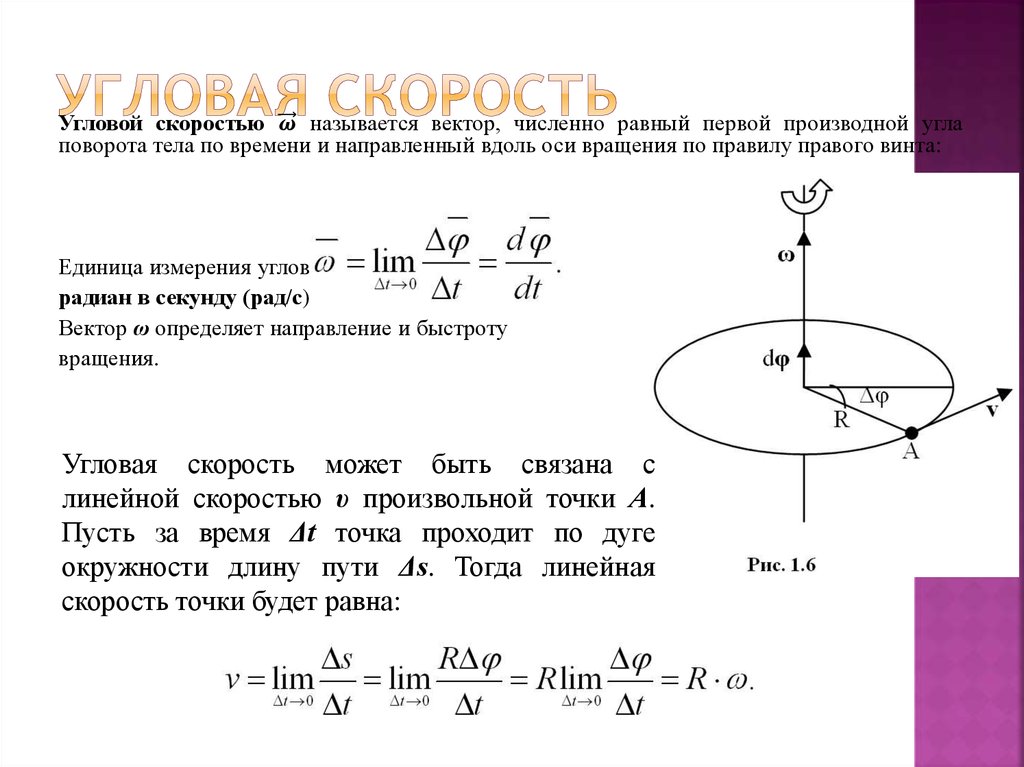
Когда материальная точка движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности. Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:

w = φ / t, где:

φ – угол поворота радиуса,

t – период времени вращения.

Единицы измерения величины

В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с – основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):

w = 2π*n,

где n – частота вращения.

В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют правило буравчика, которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит поступательное движение винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.

Примеры расчета

Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:

w = φ / t = 7t / t = 7 с^-1.

Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t. Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π — один полный оборот, получается следующее:

v = 2π*r / t = w * r = 7 * 0.5 = 3.5 м/с

Вот еще одна задачка на эту тему. Известно, что радиус Земли на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:

w = 2π*n = 2*3,14 *(1/(24*3600)) = 7,268 *10^-5 рад/с.

Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10^-5 *6370 * 1000 = 463 м/с.

Равномерное движение по окружности. Скорость, ускорение

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.

Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:

. (1)

Частота обращения — это величина, обратная периоду:

.

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.

Угловая скорость.

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

. (2)

Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому

. (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

. (4)

Закон движения.

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

.

Но из формулы (2) имеем: . Следовательно,

. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

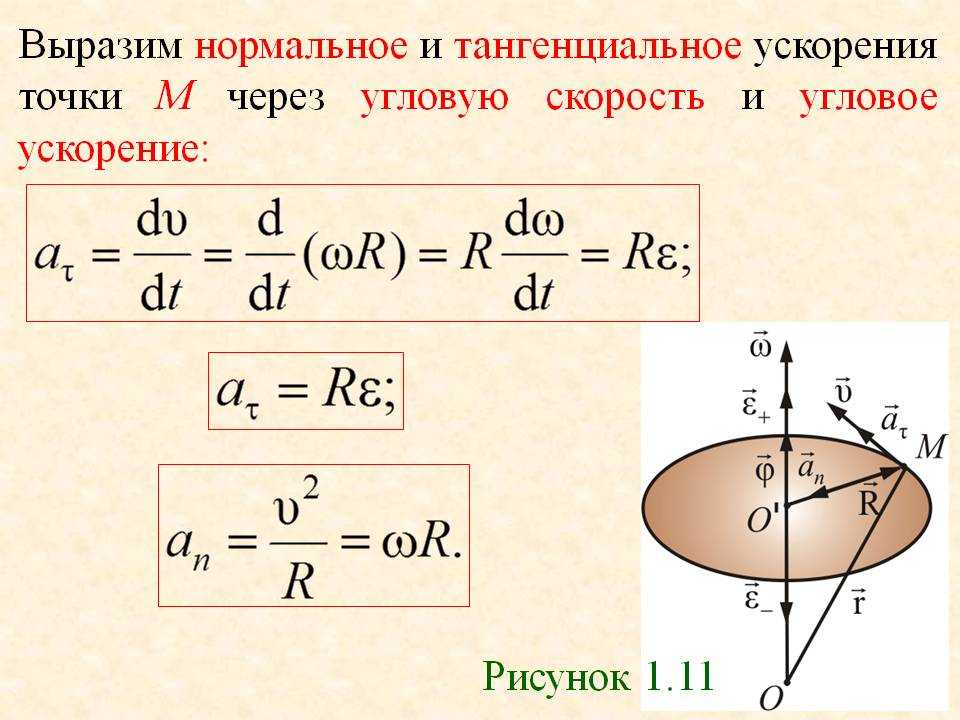
Центростремительное ускорение.

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

С учётом формул (5) имеем:

(6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

(7)

где — радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

(8)

Выразим угловую скорость из (4)

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

.

Формула угловой скорости — Определение скорости вращения и проблемы

Ранее мы изучали темы угловой скорости, поэтому здесь мы обсудим формулу угловой скорости. Формула угловой скорости используется для расчета расстояния, пройденного одним конкретным телом, с точки зрения оборотов или оборотов за затраченное время.

Скорость зависит от того, насколько медленно или быстро движется объект. Мы уже слышали о скорости, но знаем ли мы, что мы говорим о конкретном типе скорости здесь. Так что, если мы не слышали об угловой скорости, то мы попали по адресу. Более того, мы узнаем о разнице между угловой скоростью и угловой скоростью.

Угловая скорость, которую мы изучим, это скорость вращательного движения объекта. Формула угловой скорости обычно вычисляет расстояние, пройденное телом, в терминах оборотов или вращений за затраченное время. Говорят, что оно обозначается буквой или символом ω и задается следующим образом:

Угловая скорость = \[\frac{Общее пройденное расстояние}{Общее затраченное время}\]

Круговое или вращательное движение

Что именно делать мы подразумеваем под круговым движением или вращением? Вращательное движение — это круговое движение объекта вокруг оси вращения, когда объект движется по круговой траектории. Например, круговые движения включают в себя гоночный автомобиль, мчащийся по круговой кривой, или игрушку, которая прикреплена к веревке, раскачивающейся по кругу, или круговую петлю на американских горках. Другими примерами являются вращение колеса на своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступления на Олимпийских играх. Мы можем заметить, что иногда объекты будут вращаться во время кругового движения, как планета Земля, которая вращается вокруг своей оси, вращаясь вокруг Солнца.

Когда мы решаем задачи, связанные с вращательным движением, мы используем переменные, аналогичные линейным переменным, такие как расстояние, скорость, ускорение и сила. но мы должны заметить, что он учитывает кривизну вращения движения. Здесь мы обычно определяем угол поворота, который является угловой эквивалентностью расстояния, и угловой скоростью, которая является угловой эквивалентностью линейной скорости.

Как найти угловую скорость

Скорость, известная как угловая скорость, является мерой того, насколько быстро центральный угол вращающегося тела изменяется во времени. Формула угловой скорости — это отношение между угловой скоростью и скоростью, которое является линейным, наряду с несколькими проблемами угловой скорости.

Термин скорость, который ранее использовался в различных контекстах. Например, мы должны знать, с какой скоростью мы ведем машину или как быстро мы бросаем мяч. Точно так же скорость в основном относится к тому, насколько медленно или, как мы можем сказать, быстро движется объект. Таким образом, угловая скорость — это скорость вращения объекта. Другими словами, это описывается как изменение угла объекта в единицу времени.

Следовательно, если мы хотим рассчитать скорость вращательного движения, нам потребуется его угловая скорость. Формула угловой скорости вычисляет расстояние, которое преодолевает тело, в пересчете на число оборотов или оборотов за затраченное время.

Кроме того, здесь очень важен радиан. Для расчета угловой скорости мы измеряем угол в радианах. Говорят, что радианы — это способ измерения углов, где мы определяем прямой угол как пи/2 радиана. Следовательно, один полный оборот будет содержать около 6,28 радиана.

Мы видим, что угловая скорость — это скорость, с которой объект меняет свои углы, которые мы измеряем в радианах за заданное время. Угловая скорость имеет величину, которая является только значением.

Символ ω = \[\frac{\Theta}{t}\]

Где:

• Символ ω относится к угловой скорости в радианах/сек.

• Символ θ — это угол в радианах (2π радиан = 360 градусов).

• t относится ко времени, сек.

Важно отметить, что угловая скорость и угловая скорость используют одну и ту же формулу. Однако разница между ними заключается в том, что угловая скорость является скалярной величиной, тогда как угловая скорость является векторной величиной.

Формула угловой скорости

Линейная скорость, при которой мы уже имеем точку на вращающемся объекте, зависит от его расстояния от центра вращения. Угловая скорость, которую мы знаем, — это угол, на который обычно движется объект за определенный промежуток времени. Угловая скорость измеряется в радианах в секунду, рад/с. В полном круге 2π радиан. На расстоянии r от центра вращения находится точка объекта, которая имеет линейную скорость, равную угловой скорости, умноженной на расстояние r. Единицей линейной скорости является метр в секунду, м/с.

Линейная скорость = угловая скорость x радиус вращения

v = ωr

v = линейная скорость (м/с)

ω = угловая скорость (радиан/с)

r = радиус вращения вращение (м)

Преобразование градусов в радианы и радианы в градусы.

Угол поворота часто измеряется в радианах. (Радианы — безразмерные единицы, определяемые как отношение двух расстояний, радиуса и длины дуги.) 

Один полный оборот по окружности круглого объекта покрывает 2π радиан или 360 ^o градусов. Радиан и градус взаимопреобразуемы, и мы можем преобразовать их, используя это соотношение Скорость (или скорость) Формула

Пример 1: Земле требуется целый год (365 дней), чтобы совершить один оборот вокруг Солнца. Вычислите угловую скорость, с которой Земля вращается вокруг Солнца.

Решение: плоской Земле требуется целый год, чтобы совершить один оборот вокруг Солнца. Таким образом, время в секундах будет

t = 265 × 24 часа × 60 мин/час × 60 секунд/мин = 31,53,60,00 секунды.

Земля совершает один полный оборот, а один оборот охватывает 360°, поэтому можно записать как = 2π.

И после подстановки этих значений в формулу угловой скорости,

Угловая скорость (ω)    = \[\frac{Общее пройденное расстояние}{Общее затраченное время}\]= \[\frac{\Theta}{t} \]                               

        = \[\frac{2\pi }{31,53,60,00сек}\] = 1,9923 × 10-7 рад/сек.

Таким образом, угловая скорость Земли при движении по окружности будет равна 1,9923 × 10-7 рад/сек.

Пример 2: Колеса огромного грузовика радиусом 1 м движутся со скоростью 5 м в секунду. Вычислите его угловую скорость.

Решение: Скорость движения грузовика можно рассматривать как Линейная скорость = 5 м/с,

Радиус колеса грузовика (или круговой траектории) id r = 1 м (дан)

Формула для нахождения угловой скорости ω = r   

Подставляя значения, получаем

 ω = \[\frac{5}{1}\] = 5 рад/сек.

Отсюда угловая скорость колес этого грузовика будет равна 5 рад/сек.

Формула угловой скорости — GeeksforGeeks

Скорость — это просто, как вы знаете, мера того, насколько быстро или медленно движется объект, например, как быстро вы ведете машину. Здесь мы говорим о конкретном типе скорости. Угловая скорость — это только тип скорости, но здесь тело должно двигаться по круговой траектории.

Формула угловой скорости

Угловая скорость определяется как скорость изменения углового смещения, то есть угол, на который проходит тело по окружности. Угловая скорость рассчитывается как количество вращений/оборотов, сделанных телом за затраченное время. Угловая скорость обозначается греческой буквой «ω», известной как омега. Единицей угловой скорости в системе СИ является рад/с.

Угловая скорость рассчитывается по двум различным формулам:

• ω = θ/t
• ω = v/r

Вывод формулы

Рассмотрим тело, движущееся по окружности радиусом r, показанной выше, с линейной скоростью v. Предположим, что тело движется из точки А в точку В. пройти расстояние s по дуге окружности и пересечь угол θ за период времени t.

Круговой путь, пройденный телом

Как известно, угловая скорость есть скорость изменения смещения – Угловая скорость, ω = θ/t

Таким образом, формула для угловой скорости равна ω = θ/t .

Другая формула для угловой скорости

Несмотря на приведенную выше формулу, существует другая и более широко используемая формула для расчета угловой скорости с точки зрения конкурсных экзаменов.

Поскольку ω = θ/t ⇢ (1)

Теперь мы знаем, что расстояние, пройденное по дуге окружности, равно произведению радиуса на пройденный угол. Итак,

s = rθ

=> θ = s/r ⇢ (2)

Из (1) и (2)

ω = s/(rt) ⇢ (3)

Также из общего понимания линейных скоростей, 

v = с/т ⇢ (4)

Из (3) и (4),

ω = v/r

Примеры задач

3

3

3 1: Рассмотрим тело, движущееся по окружности радиусом 5 м. Он покрывает половину оборота за 5 с. Вычислите его угловую скорость.

Решение: 

При половине оборота пройденный угол составляет 180 градусов. В радианах это равно π радианам.

ω = θ/t

=> ω = π/5 = 0,628 рад/с

Вопрос 2: Колесо автомобиля радиусом 2 м вращается с линейной скоростью 10 м/с. Вычислите его угловую скорость.

Решение:

ω = v/r

ω = 10/2

= 5 рад/с

Вопрос 3. ч, а радиус пути 0,2 м. Вычислите угловую скорость автомобиля.

Solution: 

v = 18 km/hr = 5 m/s

r = 0.2 m

ω = v/r 

= 5/0.2 

= 25 rad/s

Вопрос 4: Автомобиль движется по окружности радиусом 2 м с угловой скоростью 2 рад/с. Вычислите угол в градусах, на который автомобиль повернется за 2 с.