Содержание
Угловая скорость
Ландсберг Г.С.
2010-03-24 22:32
(0)
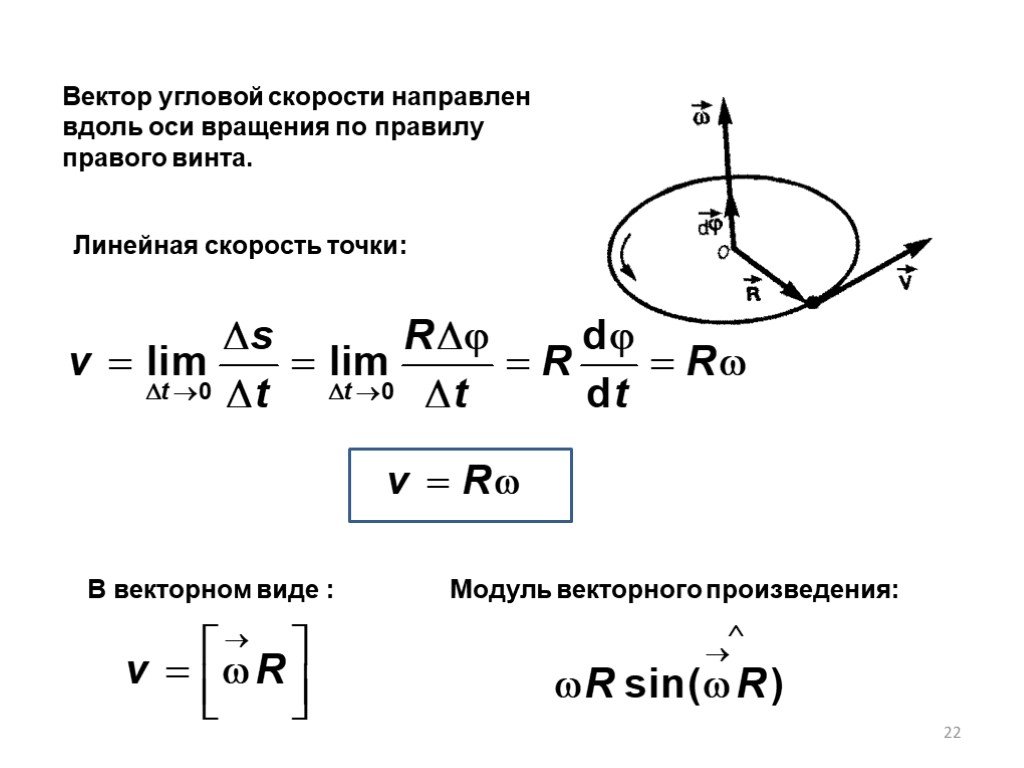
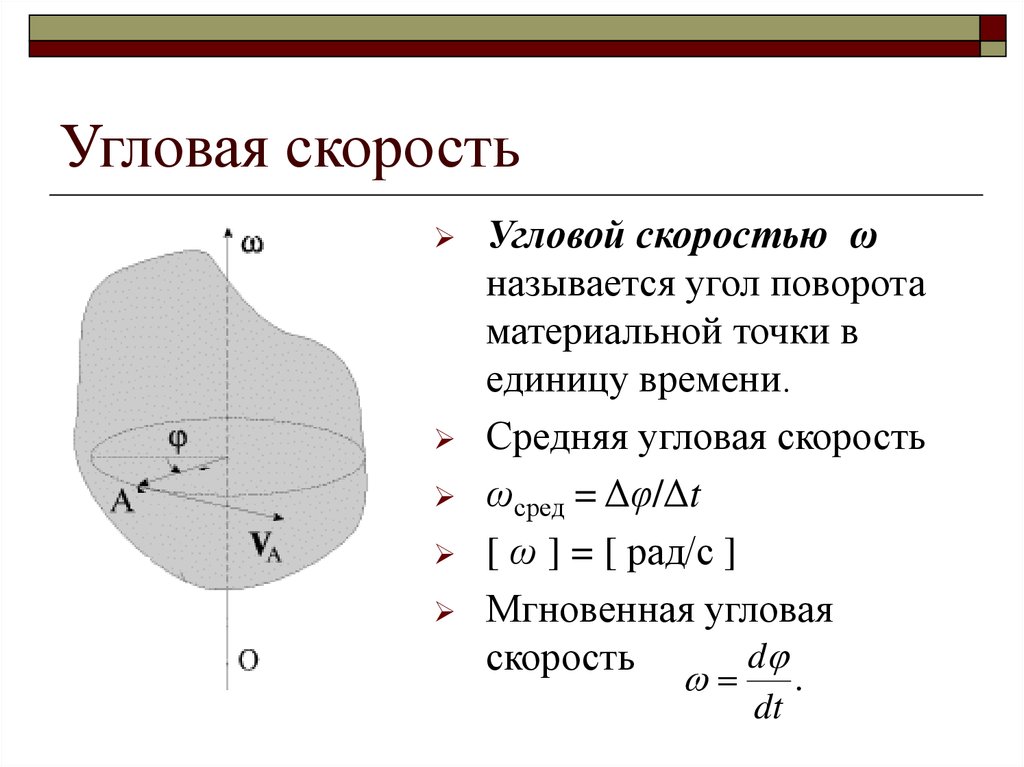
Движение точки по окружности можно характеризовать углом поворота радиуса, соединяющего движущуюся точку с центром окружности. Изменение этого угла с течением времени характеризуют угловой скоростью. Угловой скоростью точки называют отношение угла поворота радиус-вектора точки к промежутку времени, за который произошел этот поворот. Угловая скорость численно равна углу поворота радиус-вектора точки за единицу времени.
Угол поворота обычно измеряют в радианах (рад.). Единицей угловой скорости служит радиан в секунду (рад/с) — угловая скорость, при которой точка описывает дугу, опирающуюся на угол, равный одному радиану, за одну секунду.
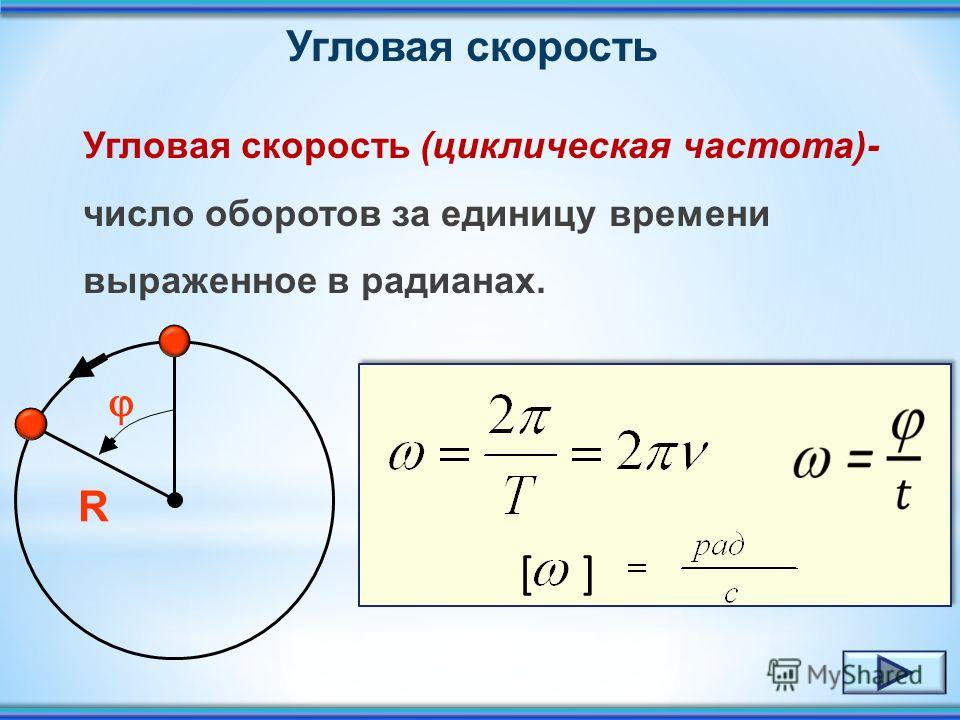
Полный оборот по окружности составляет
рад. Значит, если точка вращается с частотой
, то ее угловая скорость есть
рад/с.
Если движение точки по окружности неравномерно, то можно ввести понятие средней угловой скорости и мгновенной угловой скорости, как это делалось для обычной скорости в случае неравномерного движения, В дальнейшем, однако, будем рассматривать только равномерное движение по окружности.
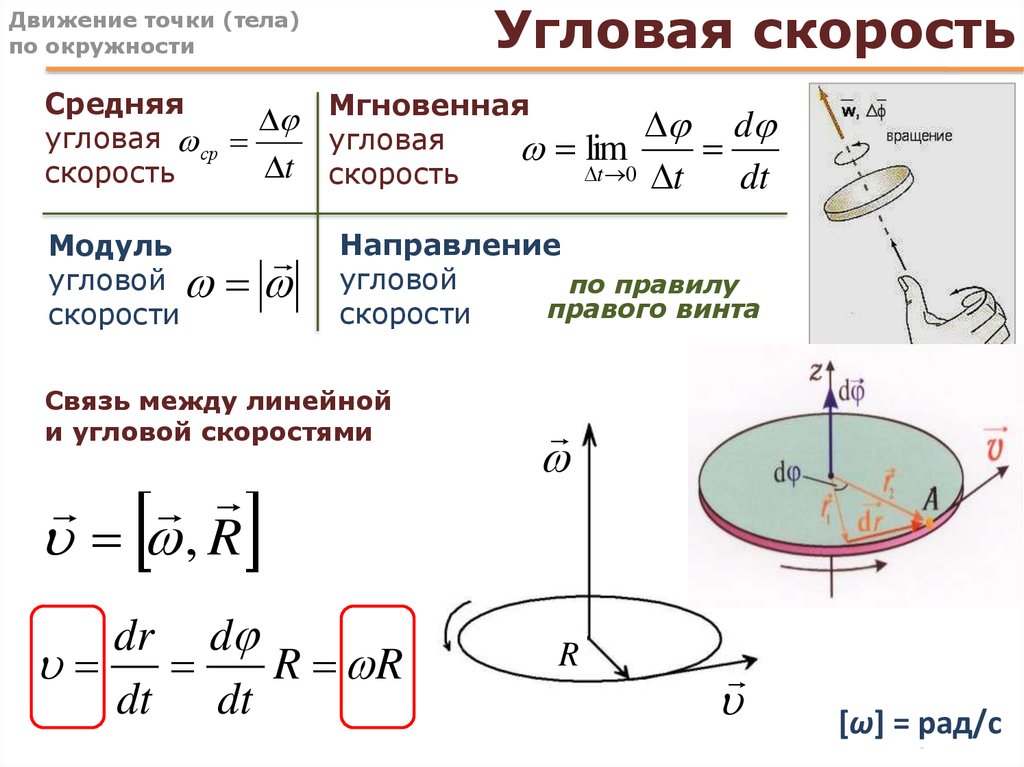
«Обычную» скорость будем, в отличие от угловой скорости, называть линейной скоростью. Легко найти связь между линейной скоростью точки
, ее угловой скоростью
и радиусом
окружности, по которой она движется. Так как, описав угол, равный одному радиану, точка пройдёт по окружности расстояние, равное радиусу, то
, (115.1)
т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности.
Пользуясь (115.1), можно выразить центростремительное ускорение точки при движении по окружности через угловую скорость. Подставляя выражение для скорости (115.1) в (27.1), найдем формулу, выражающую центростремительное ускорение через угловую скорость!
. (115.2)
При рассмотрении вращения твердого тела вокруг оси также используется понятие угловой скорости в этом случае угловая скорость у всех точек тела одинакова, так как все они поворачиваются на один и тот же угол. Таким образом, вращение твердого тела вокруг оси можно охарактеризовать угловой скоростью, с которой движутся все его точки.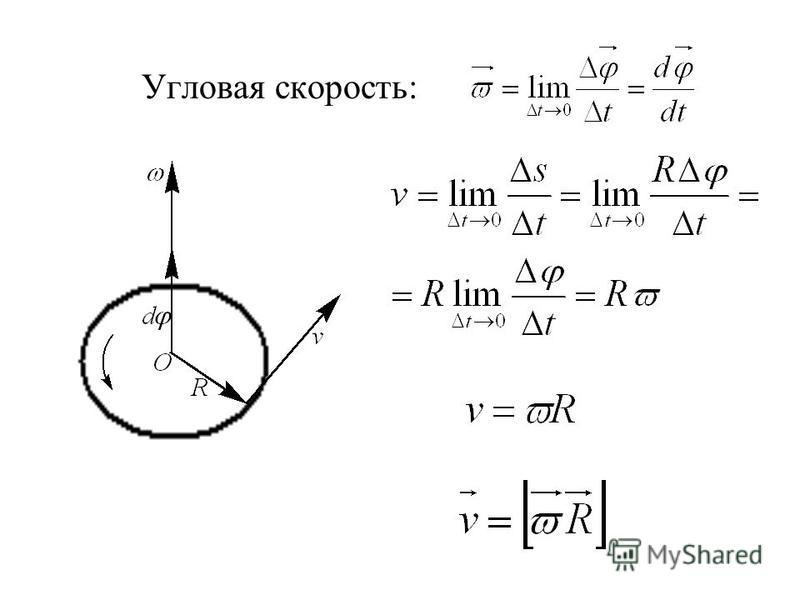 Поэтому будем называть ее угловой скоростью тела. Из формул (115.1) и (115.2) видно, что при вращении твердого тела линейные скорости его точек и их центростремительные ускорения пропорциональны расстоянию от этих точек до оси вращения.
Поэтому будем называть ее угловой скоростью тела. Из формул (115.1) и (115.2) видно, что при вращении твердого тела линейные скорости его точек и их центростремительные ускорения пропорциональны расстоянию от этих точек до оси вращения.
115.1
. Две точки движутся с одинаковыми угловыми скоростями по окружностям, радиусы которых относятся, как 1:2. Найдите отношение ускорений этих точек.
115.2.
Что больше: угловая скорость вращения часовой стрелки часов или угловая скорость вращения Земли?
Видео
-
Физика воздуха. Сжимаемость воздуха.
2020-05-23
-
Что такое электричество? | ПРОСТО ФИЗИКА с Алексеем Иванченко
2020-05-23
-
Курс подготовки к ЕГЭ. Физика. Урок №1 Кинематика равномерного движения
2018-12-22
-
Батавские слезки — опыты
2017-12-15
-
Тепловой рычаг — физические опыты
2017-12-15
-
Секрет ЖК-монитора — поляризационная пленка
2017-12-15
-
ЛАЗЕР В ВОДЕ — физические опыты
2017-12-15
-
ЭЛЕКТРОХРОМНАЯ ПЛЕНКА с токопроводящим слоем и жидкокристаллической основой
2017-12-15
-
Урок из космоса.
 Физика невесомости
Физика невесомости2017-12-12
-
Абсолютный ноль — погоня за абсолютным нулём
2017-12-12
5 ответов, которые вы должны знать
Обороты в минуту (обороты в минуту) и угловая скорость определяют скорость вращающегося тела. Давайте обсудим, как изменить обороты на угловую скорость.
Преобразование оборотов в угловую скорость или наоборот может быть выполнено просто для определения скорости объекта. В физике или машиностроении обе эти концепции определяют, насколько быстро частица или объект вращаются вокруг своей фиксированной оси или по круговой траектории.
Так же, как линейное движение, есть и вращательное движение. Быстрота вращающегося тела определяется его угловой скоростью. Например, колесо движущегося автомобиля вращается вокруг неподвижной оси и по круговой траектории. Благодаря этому движению угол продолжает изменяться, и угловая скорость возникает.
Изображение Фото: DNET на основе растровой версии, выпущенной под GFDL, Угловая скорость, CC BY-SA 3. 0
0
Угловая скорость или скорость вращающегося тела определяет, насколько быстро происходит вращение по круговой траектории. Его единица равна радианам в секунду. Полный круг имеет длину 360°, поэтому, если частица совершает 1 полный оборот за 1 секунду, то ее угловая скорость будет равна 360 градусам в секунду. В радианах на секунду угловая скорость будет равняться 2π радианам в секунду, так как 360° равно 2π радианам.
Число оборотов в минуту (оборотов в минуту) также определяет, насколько быстро тело вращается. 1 полный оборот объекта составляет 1 оборот. Скорость объекта становится совершенными оборотами в минуту.
Мы можем преобразовать обороты в угловую скорость всего за несколько простых шагов. Стандартная единица угловой составляющей скорости — радиан в секунду. Поэтому для преобразования количество оборотов в минуту необходимо изменить на радианы в секунду.
1 полный оборот, совершенный вращающимися объектами, равен 360 °. А 360 ° радиан равняется 2π радиан. Следовательно, 1 оборот равен 2π радианам;
1 оборот = 2π радиан
Кроме того, мы знаем, что 1 мин = 60 секунд.
Следовательно, обороты до угловой скорости становятся;
1 оборот/1минута=2π радиан/60 секунд
Таким образом, мы имеем;
1 об/мин=2π/60 рад.с-1
Соотношение между оборотами в минуту и угловой скоростью становится;
ω=2π/60 об/мин
Например, прялка вращается со скоростью 300 об / мин. Мы можем найти угловую скорость как;
Первый шаг — перевести количество оборотов в радианы.
1 оборот = 2π
300 оборотов = 300 x 2π = 600 π
Второй шаг — перевести минуты в секунды.
1 минута = 60 секунд
Теперь угловая скорость будет
ω=радиан/секунду
ω=600π/60
ω=10рад.с-1
Предположим, велосипедная шина диаметром 20 дюймов совершает 420 оборотов за 1 минуту. Тогда угловая скорость шин будет;
об/мин=обороты/время
ω=2π/60*об/мин
ω=2π/60*420
ω=4πрад.с-1
Часто задаваемые вопросы (FAQ)
Объясните угловую скорость на примере.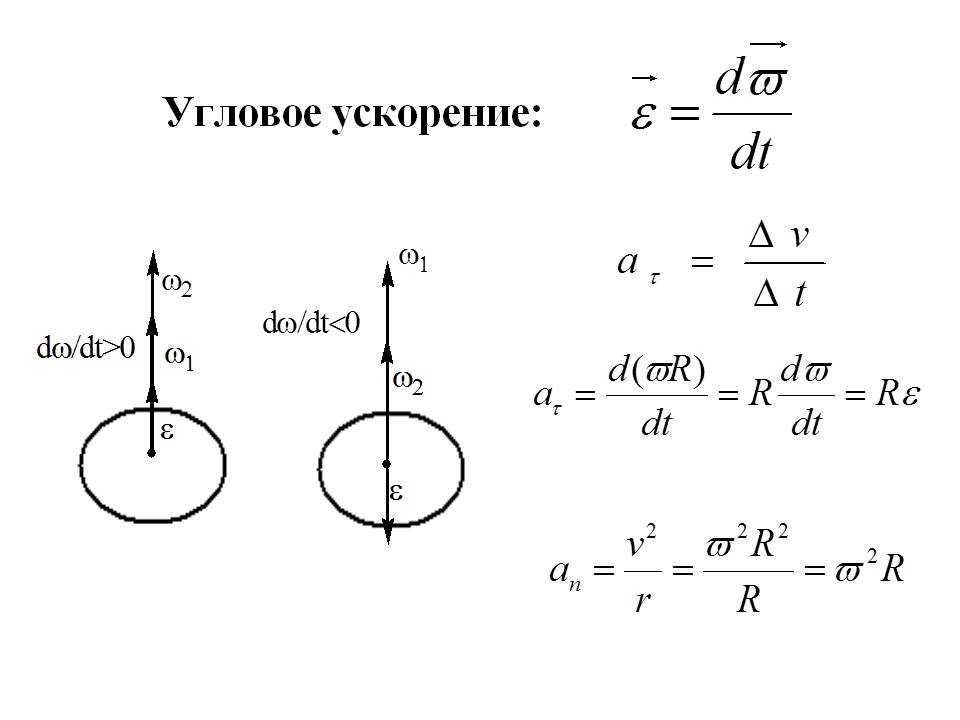
Изменение угла вращающегося тела составляет его угловую скорость.
Предположим, вращается прялка. При этом он будет двигаться по круговой траектории. Теперь он движется из точки А в точку В, делая угол тета за t секунд. Следовательно, угловая скорость колеса будет равна ω=θ/т . Единица угловой скорости — радиан в секунду.
Является ли угловая скорость векторной величиной?
Угловая скорость равна векторное количество с величиной и направлением. Направление угловой скорости действует вдоль оси вращения тела.
Что означает обороты?
Обороты обозначают оборот в минуту. Для вращающегося тела количество оборотов, совершаемых за одну минуту, определяет его скорость.
Какова угловая скорость секундной стрелки часов?
Секундная стрелка часов — это основной пример угловой скорости.
Секундная стрелка часов совершает полный оборот за одну минуту.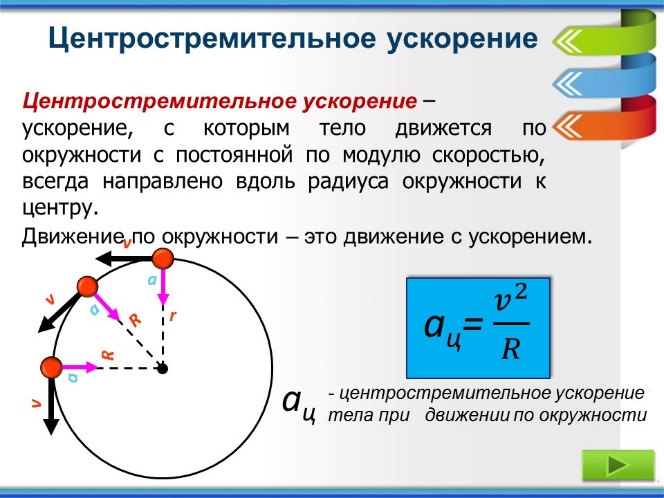 Мы знаем, что 1 оборот равен 2π радиан, а 1 минута равна 60 секундам. Следовательно, угловая скорость секундной стрелки равна:
Мы знаем, что 1 оборот равен 2π радиан, а 1 минута равна 60 секундам. Следовательно, угловая скорость секундной стрелки равна:
ω=2π/60
ω=π/30
ω=0.105рад.с-1
Как преобразовать обороты в угловую скорость?
Число оборотов в минуту можно преобразовать в угловую скорость за несколько простых шагов.
Обороты — это количество оборотов в минуту. 1 оборот равен 360 °, а 360 ° равняется 2π радианам. Поэтому у нас есть;
1 оборот = 2π радиан
Во-вторых, 1 минута равна 60 секундам.
Таким образом, мы имеем;
1 об/мин=2π/60 рад.с-1
ω=2π/60*об/мин
Угловая скорость и ускорение — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты
170 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 Следующая →
AP Physics 1 Справка »
Ньютоновская механика »
Круговое, вращательное и гармоническое движение »
Круговое и вращательное движение »
Угловая скорость и ускорение
Горизонтально установленное колесо радиуса сначала находится в состоянии покоя, а затем начинает постоянно ускоряться, пока не достигнет угловой скорости после 5 полных оборотов. Чему равно угловое ускорение колеса?
Чему равно угловое ускорение колеса?
Возможные ответы:
Правильный ответ:
Пояснение:
Вы можете вспомнить кинематическое уравнение, которое связывает конечную скорость, начальную скорость, ускорение и расстояние соответственно:
Что ж, для вращательного движения (например, в этой задаче) есть аналогичное уравнение, за исключением того, что оно связывает конечную угловую скорость, начальную угловую скорость, угловое ускорение и угловое расстояние соответственно:
Колесо начинает в состоянии покоя, поэтому начальная угловая скорость равна нулю. Общее количество оборотов колеса равно 5 оборотам. Каждый оборот эквивалентен угловому расстоянию в радианах. Таким образом, мы можем преобразовать общее количество оборотов в угловое расстояние, чтобы получить:
Конечная угловая скорость дана как в тексте вопроса. Таким образом, мы должны использовать приведенное выше уравнение для решения углового ускорения.
Таким образом, мы должны использовать приведенное выше уравнение для решения углового ускорения.
Сообщить об ошибке
Объект движется с постоянной скоростью по окружности радиусом 1,5 м. Чему равно угловое ускорение тела?
Возможные ответы:
Правильный ответ:
Объяснение:
Для вращающегося объекта или объекта, движущегося по круговой траектории, отношение между угловым ускорением и линейным ускорением составляет
Линейное ускорение определяется выражением , угловое ускорение равно , а радиус круговой траектории равен .
Для кругового/центростремительного движения линейное ускорение связано с линейной скоростью объекта как
Мы знаем, что линейная скорость равна , а радиус равен 1,5 м, поэтому мы можем найти линейное ускорение…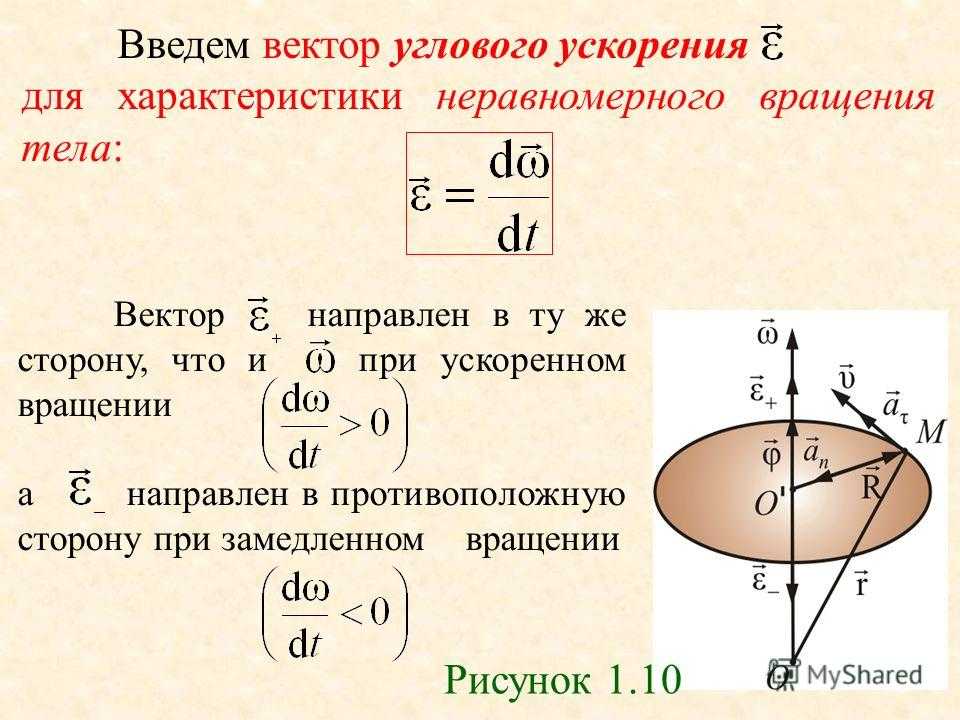
Теперь, когда у нас есть линейное ускорение, мы можем использовать его в уравнении вверху, чтобы найти угловое ускорение…
Сообщить об ошибке
Если велосипедному колесу требуется 3 секунды, чтобы завершить одно оборот, чему равна угловая скорость колеса?
Возможные ответы:
Правильный ответ:
Объяснение:
Определение угловой скорости .
Идентифицируя данную информацию как и , мы можем включить это в уравнение для расчета угловой скорости:
Сообщить об ошибке
Какова угловая скорость секундной стрелки часов?
Возможные ответы:
Правильный ответ:
Пояснение:
Угловую скорость секундной стрелки часов можно найти, разделив число радиан, которое секундная стрелка пройдет за известный период времени. К счастью для часов, мы знаем, что секундная стрелка сделает один оборот, т. е. пройдет за одну минуту или 60 сек. Формула угловой скорости: 9
К счастью для часов, мы знаем, что секундная стрелка сделает один оборот, т. е. пройдет за одну минуту или 60 сек. Формула угловой скорости: 9
Сообщить об ошибке 5 метров на большой башне с часами?
Возможные ответы:
Без разницы
Секундная стрелка башенных часов имеет угловую скорость в 500 раз медленнее, чем у наручных часов
Секундная стрелка башенных часов имеет угловую скорость в 5 раз больше, чем наручные часы
Секундная стрелка башни с часами имеет угловую скорость в 500 раз больше, чем скорость наручных часов
Секундная стрелка башни с часами имеет угловую скорость в 20 раз больше, чем скорость наручных часов
Правильный ответ:
Нет разница
Объяснение:
Угловая скорость не должна изменяться в зависимости от радиуса секундной стрелки. Неважно, какого размера секундная стрелка, она все равно будет делать один оборот в минуту или 60 секунд. Линейная скорость будет больше, и угловой момент также будет больше для башни с часами, но ее угловая скорость будет той же. Это можно увидеть, взглянув на уравнение для угловой скорости:
Линейная скорость будет больше, и угловой момент также будет больше для башни с часами, но ее угловая скорость будет той же. Это можно увидеть, взглянув на уравнение для угловой скорости:
Сообщить об ошибке
Продолжительность поездки колеса обозрения составляет 3 минуты, то есть ему требуется три минуты, чтобы совершить один полный оборот. Какова угловая скорость колеса обозрения, если оно перевозит пассажиров только один раз за ?
Возможные ответы:
Правильный ответ:
Объяснение:
Угловая скорость, дюйм, равна пройденному расстоянию, деленному на время, затраченное на прохождение этого участка:
Нам говорят, что время, необходимое для совершения одного оборота, составляет 3 минуты. Один оборот равен , а 3 минуты равны 180 секундам. Разделите значение в радианах на значение в секундах, чтобы получить угловую скорость.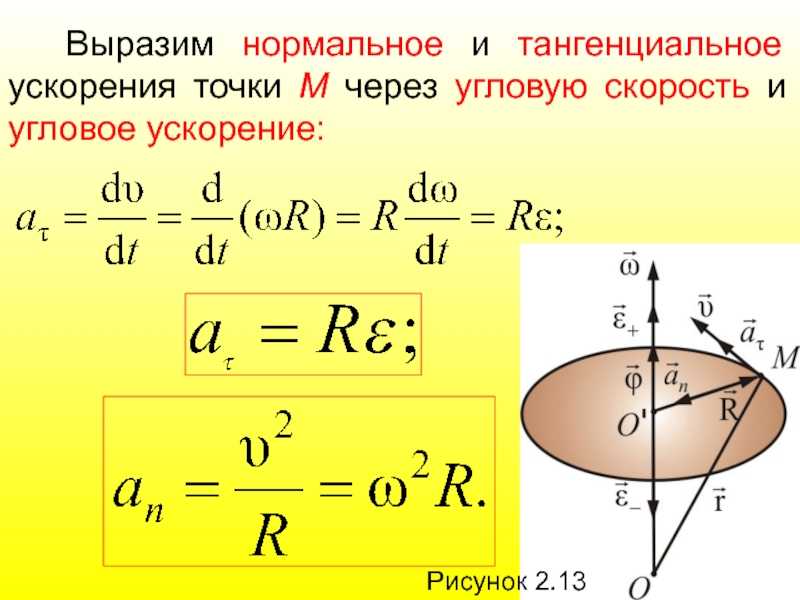
Сообщить об ошибке
Колесо совершает один полный оборот каждую секунду и имеет радиус . Определите его угловую скорость.
Возможные ответы:
Правильный ответ:
Объяснение:
Для этого вопроса угловая скорость может быть задана уравнением:
, где это угол, а это время, затрачиваемое на этот угол.
В этой задаче колесо делает один полный оборот() за секунды.
Следовательно:
Сообщить об ошибке
Компакт-диск вращается со скоростью в положительном направлении против часовой стрелки. После нажатия кнопки воспроизведения диск ускоряется со скоростью . Какова угловая скорость компакт-диска через 4 секунды?
Возможные ответы:
Правильный ответ:
Объяснение:
Учитывая начальную угловую скорость, угловое ускорение и время, мы можем легко найти конечную угловую скорость с помощью:
Сообщить об ошибке
Если колесо обозрения имеет высоту 100 м, найдите угловую скорость в оборотах. в минуту, если едут всадники в телегах.
в минуту, если едут всадники в телегах.
Возможные ответы:
Ничего из перечисленного
Объяснение:
Если колесо обозрения имеет высоту, то оно должно иметь и радиус .
Окружность колеса обозрения, или расстояние одного оборота, тогда:
Преобразуйте заданную скорость в метры в минуту, или :
Найдите число оборотов в минуту:
Сообщить об ошибке
Массовый человек едет на колесе обозрения радиусом . Колесо вращается с постоянной угловой скоростью . Определить линейную скорость наездника.
Возможные ответы:
Правильный ответ:
Объяснение:
Преобразовать в:
Сообщить об ошибке
← Назад 1 2 Далее →
Уведомление об авторских правах
Все ресурсы AP Physics 1
7 Диагностические тесты
170 практических тестов
Вопрос дня
Карточки
Learn by Concept
Физика — Кинематика — Угловая скорость
Резюме
Когда мы работаем в двухмерной плоскости, мы можем представить угловую скорость одним числом. В трех измерениях мы можем представить угловую скорость как трехмерную векторную величину (w x , w y , w z ). В этой форме угловые скорости можно комбинировать с помощью сложения векторов.
В трех измерениях мы можем представить угловую скорость как трехмерную векторную величину (w x , w y , w z ). В этой форме угловые скорости можно комбинировать с помощью сложения векторов.
Это отличается от конечных вращений (как описано на этой странице), которым нужны дополнительные измерения, чтобы избежать сингулярностей и правильно комбинировать конечные вращения.
Двухмерный случай
С линейным движением все относительно просто, мы просто используем v = dx/dt, скорость ‘v’ — это скорость изменения расстояния во времени, мы рассматриваем ее как то же самое, что и dx/dt
Если мы работаем в двух измерениях, то мы можем определить угловую скорость ‘w’ аналогичным образом:
w = d angle/dt
Другими словами, если мы измеряем угловую скорость движущейся точки, — это скорость изменения угла, который он делает, по сравнению с некоторым исходным направлением. Конечно, это будет зависеть от точки, от которой мы измеряем угол.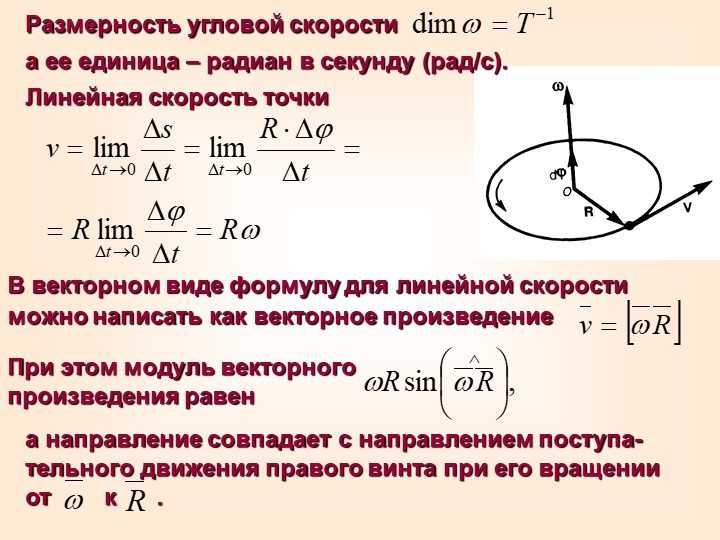 В некоторых случаях это легко понять, например, если мы измеряем угловую скорость твердого тела, вращающегося вокруг своего центра масс, то мы обычно измеряем угол некоторой точки относительно центра масс. Однако не всегда очевидно, откуда мы измеряем, поэтому мы должны быть осторожны, определяя его.
В некоторых случаях это легко понять, например, если мы измеряем угловую скорость твердого тела, вращающегося вокруг своего центра масс, то мы обычно измеряем угол некоторой точки относительно центра масс. Однако не всегда очевидно, откуда мы измеряем, поэтому мы должны быть осторожны, определяя его.
Скорости тела ()
Для трехмерного твердого тела это скорости вращения, которые могут быть измерены с помощью гироскопов скорости, когда оси их датчиков совмещены с соответствующими осями координат тела; они также могут быть рассчитаны из динамических уравнений движения.
Угловая скорость может быть задана трехмерным вектором:
| w x |
| ш у |
| ш я |
Компоненты этого вектора представляют собой векторную сумму:
- w x : скорость изменения угла (в радианах)
относительно абсолютной координаты x.
- w y : скорость изменения угла (в радианах)
относительно абсолютной координаты y. - w z : скорость изменения угла (в радианах)
относительно абсолютной координаты z.
с x ,w y и w z не зависят друг от друга,
поэтому угловые скорости могут быть добавлены, если это необходимо, без каких-либо проблем
связаны с углами Эйлера. Это потому, что мы добавляем бесконечно малые углы
которые обладают теми же свойствами, что и векторы. Видеть
этот пример, который включает добавление угловых скоростей.
Коэффициенты Эйлера
Коэффициенты Эйлера — это то, что мы получаем, когда дифференцируем углы Эйлера, например:
d курс / d t
д отношение / д т
d bank / d t
На первый взгляд может показаться, что коэффициенты Эйлера совпадают с коэффициентами тела, описанными выше, однако это не так. Если твердый объект вращается с постоянной скоростью, то скорость его тела (w x , w y , w z ) будет постоянной, однако скорости Эйлера будут все время меняться в зависимости от некоторой триггерной функции мгновенный угол между телом и абсолютными координатами. Таким образом, коэффициенты Эйлера очень запутаны, у них есть особенности, и они не имеют большого практического применения.
Таким образом, коэффициенты Эйлера очень запутаны, у них есть особенности, и они не имеют большого практического применения.
Таким образом, основная причина упоминания коэффициентов Эйлера здесь состоит в том, чтобы провести различие с коэффициентами тела и предупредить людей, чтобы они избегали использования коэффициентов Эйлера.
Представление угловой скорости с помощью оси-угла
См. эту страницу для обозначения оси-угла для конечных поворотов.
Представьте твердый объект, который одновременно вращается вокруг осей x, y и z,
угловая скорость относительно этих осей составляет w x , w y и w z .
Это вращение также может быть представлено одним вращением вокруг оси
(ж x , w y , w z) .
- угловая скорость = d угол/d t = |w(t)| = √(w x 2 +w y 2 +w z 2 ).
- нормализованная ось = (w x , w y , w z )/
|ш(т)|
| где: |
другие определения |
||
|
символ |
описание |
тип |
шт. |
| ω | угловая скорость | бивектор | с -1 |
| уголок | угол в радианах | скаляр | нет |
| т | время | скаляр | с |
| д … /дт | скорость изменения | ||
Угол оси применим только для таких непрерывных вращений, когда вращение происходит только вокруг оси, в этом случае вращение происходит в одной плоскости, и это эквивалентно случаю 2D, другими словами, ось представляет плоскость 2D, в которой мы работаем in.
На самом деле мы не можем использовать угол оси для объединения угловых скоростей в разных направлениях.
Дифференцирование матриц вращения и кватернионов
Когда мы работаем с матрицами или кватернионами, уравнение усложняется:
- для матриц это: (т)]
- для кватернионов это: d q(t) /dt = ½ * W(t) q(t)
Эти уравнения доказаны и определены ниже на этой странице.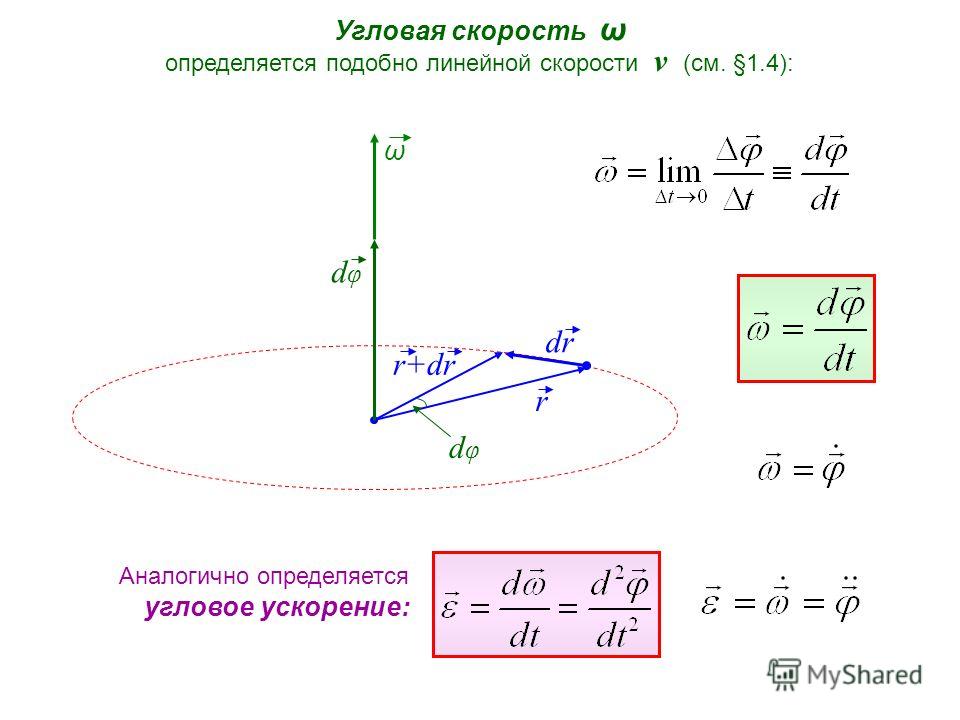
Каковы более глубокие причины этой дополнительной сложности. Я думаю, что это включает в себя следующие факторы:
- Это величины, изменяющиеся во времени, конечно, v = dx/dt также работает для величин, изменяющихся во времени, но, по крайней мере, если у нас есть постоянная скорость (и, следовательно, постоянный линейный импульс), тогда dx/dt будет постоянным. Но если [R(t)] представляет собой ориентацию объекта, вращающегося с постоянной угловой скоростью (и постоянным угловым моментом), то [d R(t)/dt] все равно будет меняться со временем, но [~w] и W(t ), используемые в приведенных выше уравнениях, не будут меняться со временем и, следовательно, являются лучшим представлением угловой скорости.
- Дифференцирование связано с операцией сложения, но повороты комбинируются с использованием матричного умножения, а не сложения. Когда я говорю «дифференцирование связано с операцией сложения», я имею в виду: когда мы прибавляем маленькое приращение ко времени, мы получаем малое приращение к расстоянию, дифференцирование есть предел при этих прибавлениях.
 Итак, существует ли математическая теория, которая связывает небольшие инкрементальные умножения с обычным дифференцированием?
Итак, существует ли математическая теория, которая связывает небольшие инкрементальные умножения с обычным дифференцированием?
Даже если мы используем матрицы или кватернионы для представления трехмерных ориентаций и вращений, когда мы переводим их в угловые скорости, мы, вероятно, захотим выразить их в виде трехмерных векторов. Значения W(t) и [~w] в приведенных выше уравнениях могут быть легко преобразованы в трехмерные векторы, W(t) уже фактически является трехмерным вектором, а кососимметричная матрица [~w] имеет все элементы трехмерного вектора. .
Причина выражения угловых скоростей в терминах трехмерных векторов заключается в том, что часто допустимо комбинировать угловые скорости путем сложения их трехмерных векторов. Таким образом, свойства угловых скоростей совершенно отличны от свойств конечных вращений.
Угловая скорость частицы
Здесь мы получаем значения вращения от точечной массы (частицы). Точка
масса не обязательно вращается вокруг своей оси (хотя могла бы, субатомная
частицы имеют спин).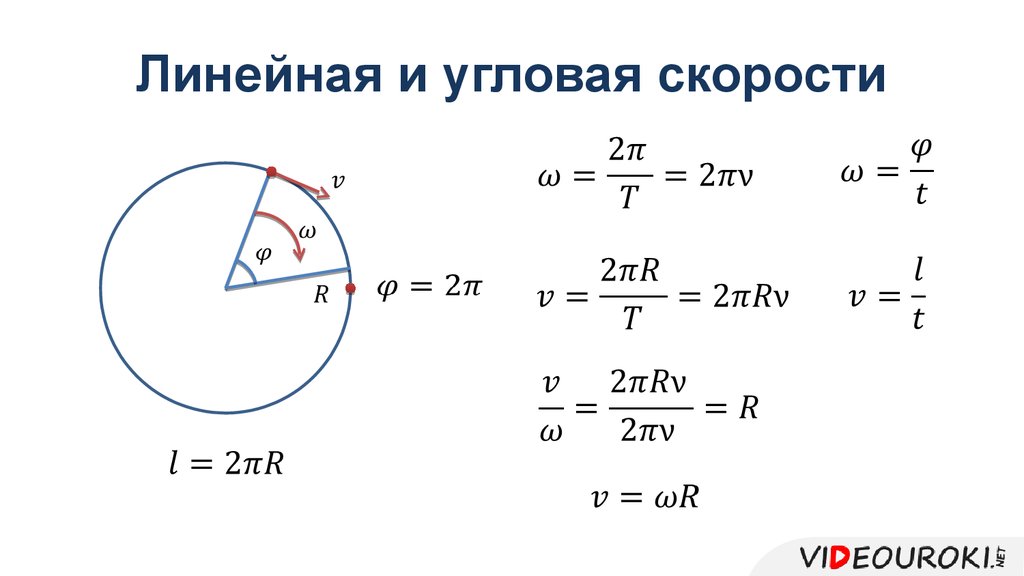 Нас здесь интересует вклад
Нас здесь интересует вклад
частица к вращательным свойствам большей массы вокруг некоторой фиксированной точки.
Для дальнейшего объяснения попробуйте прочитать числовой
методы.
Рассмотрим точку с массой .
Его линейная скорость является векторным произведением его угловой скорости относительно и его расстояния от .
dP = r dθ
Таким образом, дифференцирование обеих сторон по времени и представление в векторе
обозначение с перпендикуляром к обоим и ( находится за пределами экрана/бумаги по направлению к зрителю, обратите внимание, что мы используем правое
ручная система координат и правая
ручная линейка для положительного направления вращения)
= ×
| где: |
другие определения |
||
|
символ |
описание |
тип |
шт. |
| мгновенная линейная скорость частицы | вектор | м/с | |
| мгновенная угловая скорость о. (дθ/дт) | бивектор | с -1 | |
| мгновенное положение частицы относительно точки. — | вектор | м | |
| × | оператор векторного векторного произведения (см. здесь для определения) |
||
Таким образом, скорость вращения точки не является абсолютной величиной, а зависит
в какой точке измеряется вращение. Также частица не
должен двигаться по кругу, чтобы иметь угловую скорость, он может иметь
ненулевая угловая скорость о ,
даже если частица движется прямолинейно, при условии, что она не находится на этой прямой.
- Угловой
Скорость твердого тела - Угловой
Скорость в движущейся системе отсчета
Угловая скорость твердого объекта()
На следующих страницах будут получены величины для конечного твердого тела
тел путем интегрирования по объему. Большинство этих величин являются векторами
Большинство этих величин являются векторами
размерности 3, которая имеет компонент в направлениях x, y и z. Для обозначения
векторную величину мы показываем стрелкой над величиной, для получения дополнительной информации
о векторах см. здесь.
Рассмотрим точку массы в .
Его линейная скорость является векторным произведением его угловой скорости относительно и его расстояния от .
Как видно из раздела Угловая скорость частицы,
угловая скорость зависит от точки, вокруг которой мы измеряем вращение.
Так для твердого тела угловая скорость всех частиц, от которых
он состоит, разные.
Только когда мы измеряем вращение вокруг центра вращения,
поворот всех точек на объекте одинаковый. Итак, по этой причине, когда мы
говорят об угловой скорости твердого тела, мы имеем в виду угловую
скорость относительно его центра вращения.
Если объект движется в свободном пространстве без внешних сил или крутящих моментов
на нем, то он будет вращаться вокруг своего центра масс. Таким образом, мы можем представить
Таким образом, мы можем представить
полное мгновенное движение твердого тела за счет комбинации линейной скорости
своего центра масс и вращения вокруг своего центра масс.
Вектор угловой скорости W(t) может быть получен из углового положения как функции времени с использованием различных обозначений:
90 338 Вт (t) = d тета / dt 90 341
| в 2D (или 3D с фиксированной осью) | |
| в 3D с использованием матрицы | [~w] = [ d T(t) / dt] [T(t)] -1 |
| в 3D с использованием кватерниона | W(t) = 2 *d q(t) /dt*conj(q(t)) |
Эти выражения получены позже на этой странице.
На страницах о кинематике положение
неограниченное твердое тело было представлено 6-мерным вектором следующим образом:
| Ш x | угловая скорость относительно оси x (радиан в секунду) |
| ш у | угловая скорость относительно оси Y (радиан в секунду) |
| с с | угловая скорость относительно оси z (радиан в секунду) |
| v x | линейная скорость центра масс по оси x (метры в секунду) |
| в г | линейная скорость центра масс по оси Y (метры в секунду) |
| v з | линейная скорость центра масс по оси z (метры в секунду) |
Дополнительная информация об угловой скорости.
- Угловая скорость частицы
- Угловая скорость в движущейся системе отсчета
Представление угловой скорости с использованием матриц
Для получения информации о дифференцировании матрицы см. эту страницу.
Мы уже видели, что трехмерного вектора достаточно для хранения всех необходимых
информацию об угловой скорости. Однако могут быть ситуации, когда мы
может захотеть сохранить эту информацию в матрице. В этом случае мы можем использовать
следующая матрица:
| [~w]= |
|
Эта матрица угловой скорости связана с дифференциалом матрицы вращения следующим образом:
[~w] = [ d T(t) / dt] [T(t)] -1
Марк Иоффе любезно прислал мне вывод, который я адаптировал для использования обозначений, используемых на этом сайте.
Пусть X(t) представляет любую точку на твердом теле как вектор от начала координат и пусть:
X(t) = [T(t)] X(0)
| где: |
другое определения |
||
|
символ |
описание |
тип |
шт. |
| Х(т) | любая точка твердого тела в момент времени t как вектор от начала координат | вектор | м |
| [Т(т)] | поворот (ортогональный), который преобразует векторы при t=0 в векторы при t | матрица | нет |
| Х(0) | тот же момент времени t=0, что и вектор из начала координат | вектор | м |
дифференцирование этого уравнения дает линейную скорость точки твердого тела:
v(t) = d X(t) / dt = [ d T(t) / dt] X(0)
поскольку (0) не является функцией времени.
Обращение первого уравнения дает:
X(0) = [T(t)] -1 X(t)
, поэтому их объединение дает:
v(t) = [ d T(t) / dt] [T(t)] -1 X(t)
Из начала этой страницы мы знаем, что v(t) = w × X(t)
| где: |
другие определения |
||
|
символ |
описание |
тип |
шт. |
| в(т) | вектор линейной скорости данной частицы | вектор | м/с |
| ω | вектор угловой скорости | бивектор | с -1 |
| × | векторное перекрестное произведение | ||
| Х(т) | позиция данной частицы | вектор | м |
Мы можем преобразовать это выражение перекрестного произведения в эквивалентное матричное выражение, заменив вектор w эквивалентной матрицей [~w], известной как кососимметричная или антисимметричная матрица. который связан с вектором ω следующим образом:
который связан с вектором ω следующим образом:
| [~ω]= |
|
Объединение этих выражений для v(t) дает:
[~w] X(t) = [ d T(t) / dt] [T(t)] -1 X(t)
удаление X(t) с обеих сторон превращает это в матричное выражение для w:
[~w] = [ d T(t) / dt] [T(t)] -1
Дополнительную информацию об этом см.
здесь.
Представление угловой скорости с помощью кватернионов
Для получения информации о дифференцировании кватернионов см. эту страницу.
Если объект вращается, то кватернион, представляющий его ориентацию, будет функцией времени, поэтому мы обозначаем его q(t). Дифференциация этого определяется следующим образом:
Дифференциация этого определяется следующим образом:
d q(t) /dt = 1/2 * W(t) q(t)
| где: |
другие определения |
||
|
символ |
описание |
тип |
шт. |
| кв(т) | нормализованный кватернион, представляющий ориентацию как функцию времени | кватернион | |
| Вт(т) | вектор угловой скорости, представленный в виде кватерниона с нулевой скалярной частью, т.е. W(t) = (0, Wx(t), Wy(t), Wz(t)) |
бивектор | с -1 |
| т | время | скаляр | с |
Вывод этого любезно прислал мне Марк Иоффе здесь: pdf файл
Это расширяется с помощью правила кватерниона: ) q 2 (т) + W z (т) q 3 (т))
d q 1 (t) / dt = 1/2* (W x (t) q 0 (t) + W y (t) q 3 (t) − W z ( т) q 2 (т))
d q 2 (t) / dt = 1/2* (W y (t) q 0 (t) + W z (t) q 1 (t) − W x (t) q 3 (t))
d q 3 (t) / dt = 1/2* (W z (t) q 0 (t) + W x (t) q 2 (t) − W y ( t) q 1 (t))
ПримерПредставьте себе объект, вращающийся с постоянной скоростью w радиан в секунду вокруг оси z. q = cos(a/2) + i (x * sin(a/2)) + j (y * sin(a/2)) + k (z * sin(a/2)) где:
Таким образом, в этом случае a=w*t и x,y,z=0,0,1, поэтому q(t) = cos(вес/2) + k sin(вес/2) и, Вт(т) = кВт поэтому d q(t) /dt = 1/2 * W(t) q(t) = 1/2 * k*w*(cos(wt/2) + k sin(wt/2)) = 1/2 * w*(-sin(wt/2) + k cos(wt/2)) |
Что я действительно хочу сделать, так это показать простой способ переключения между использованием кватернионов для представления ориентации и векторов для представления угловой скорости. Я думаю, что так оно и есть, но было бы понятнее перевернуть пример, т. е.
q(t) = cos(wt/2) + k sin(wt/2)
вывести d q(t) /dt = 1/2 * w*(-sin(wt/2) + k cos(wt/2)) просто путем дифференцирования членов в приведенном выше уравнении.
затем выведите W(t) = k w из d q(t) /dt = 1/2 * W(t) q(t)
Это показывает, что, дифференцируя кватернион, мы получаем вектор.
моя предыдущая попытка вычислить это
Угловая скорость в терминах угловых скоростей Эйлера
Вектор угловой скорости в координатах тела:
Wx = скорость крена — скорость рыскания * sin(pitch)
Wy = скорость тангажа * cos (крен) + скорость рыскания * sin (крен) * cos (шаг)
Wz = yawrate * cos(roll) * cos(pitch) — pitchrate * sin(roll)
Дженни любезно прислала мне вывод этого в этом документе: pdrderivation.pdf.
Использование векторного исчисления для анализа вращения твердотельных объектов
Векторное исчисление
часто используется для анализа движения жидкостей, но нет причин, по которым
мы не должны использовать его для анализа твердых объектов при условии, что мы применяем его к
области пространства, где векторное поле непрерывно..
Если мы возьмем поле скорости вращающегося объекта, мы можем получить поле, которое
выглядит так:
Если взять завиток
этого поля мы получили бы другое векторное поле
Каждый из этих векторов имеет значение w2 в линию вдоль оси вращения
(как показано здесь)
Представление угловой скорости в программе
Угловая скорость в трехмерном пространстве может содержаться в кватернионе (см.
 Физика невесомости
Физика невесомости
 Итак, существует ли математическая теория, которая связывает небольшие инкрементальные умножения с обычным дифференцированием?
Итак, существует ли математическая теория, которая связывает небольшие инкрементальные умножения с обычным дифференцированием?
 Из этой страницы мы знаем, что:
Из этой страницы мы знаем, что: