Содержание
Угловая скорость: формула частоты вращения
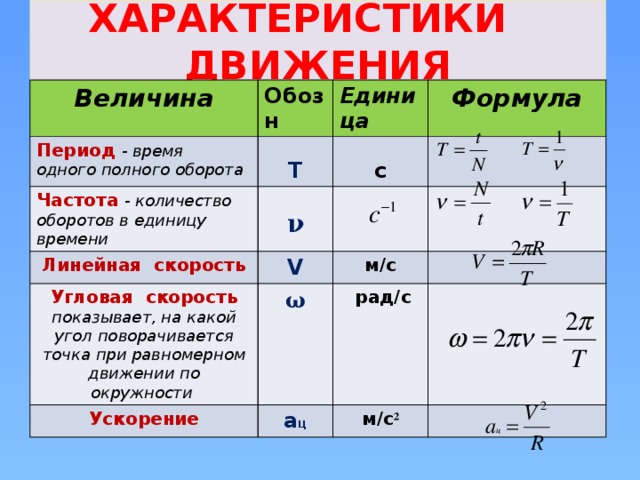
Иногда применительно к автомобилям всплывают вопросы из математики и физики. В частности, одним из таких вопросов является угловая скорость. Она имеет отношение как к работе механизмов, так и к прохождению поворотов. Разберёмся же, как определить эту величину, в чём она измеряется и какими формулами тут нужно пользоваться.
Содержание
- Как определить угловую скорость: что это за величина?
- Формула времени, за которое вращается точка по окружности заданного радиуса
- Угол поворота и период обращения
- Чему равна угловая скорость в конкретных случаях?
- Связь угловой и линейной скоростей
- Ускорение, момент и связь их с массой
- Шарнир как пример передачи импульса
Как определить угловую скорость: что это за величина?
С физико-математической точки зрения эту величину можно определить следующим образом: это данные, которые показывают, как быстро некая точка осуществляет оборот вокруг центра окружности, по которой она движется.
ПОСМОТРЕТЬ ВИДЕО
Эта, казалось бы, чисто теоретическая величина, имеет немалое практическое значение при эксплуатации автомобиля. Вот лишь несколько примеров:
- Необходимо правильно соотносить движения, с которыми вращаются колёса при повороте. Угловая скорость колеса автомобиля, движущегося по внутренней части траектории, должна быть меньше, чем у внешнего.
- Требуется рассчитывать, насколько быстро в автомобиле вращается коленвал.
- Наконец, сама машина, проходя поворот, тоже имеет определённую величину параметров движения – и от них на практике зависит устойчивость автомобиля на трассе и вероятность опрокидывания.
Формула времени, за которое вращается точка по окружности заданного радиуса
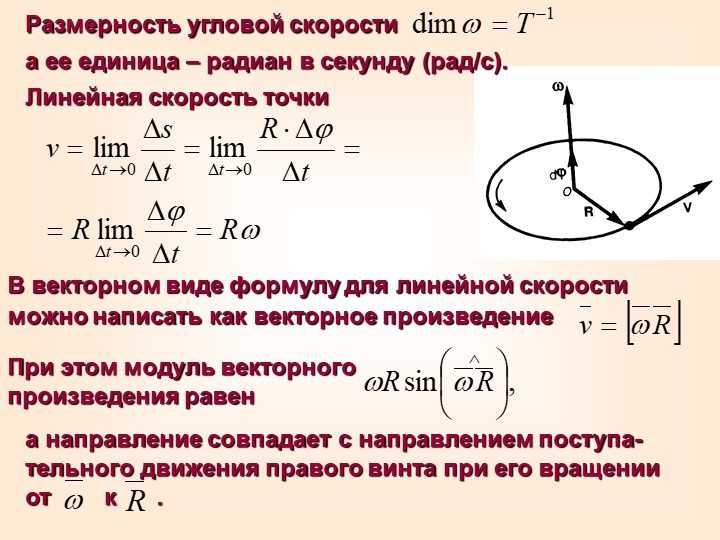
Для того, чтобы рассчитывать угловую скорость, используется следующая формула:
ω = ∆φ /∆t
Где:
- ω (читается «омега») – собственно вычисляемая величина.

- ∆φ (читается «дельта фи») – угол поворота, разница между угловым положением точки в первый и последний момент времени измерения.
- ∆t
(читается «дельта тэ») – время, за которое произошло это самое смещение. Точнее, поскольку «дельта», это означает разницу между значениями времени в момент, когда было начато измерение и когда закончено.
Приведённая выше формула угловой скорости применяется лишь в общих случаях. Там же, где речь идёт о равномерно вращающихся объектах или о связи между движением точки на поверхности детали, радиусом и временем поворота, требуется использовать другие соотношения и методы. В частности, тут уже будет необходима формула частоты вращения.
Угловая скорость измеряется в самых разных единицах. В теории часто используется рад/с (радиан в секунду) или градус в секунду. Однако эта величина мало что означает на практике и использоваться может разве что в конструкторской работе. На практике же её больше измеряют в оборотах за секунду (или минуту, если речь идёт о медленных процессах). В этом плане она близка к частоте вращения.
В этом плане она близка к частоте вращения.
Угол поворота и период обращения
Гораздо более часто, чем угол поворота, используется частота вращения, которая показывает, сколько оборотов делает объект за заданный период времени. Дело в том, что радиан, используемый для расчётов – это угол в окружности, когда длина дуги равна радиусу. Соответственно в целой окружности находится 2 π радианов. Число же π – иррациональное, и его нельзя свести ни к десятичной, ни к простой дроби. Поэтому в том случае, если происходит равномерное вращение, проще считать его в частоте. Она измеряется в об/мин – оборотах в минуту.
Если же дело касается не длительного промежутка времени, а лишь того, за который происходит один оборот, то здесь используется понятие периода обращения. Она показывает, как быстро совершается одно круговое движение. Единицей измерения здесь будет выступать секунда.
Связь угловой скорости и частоты вращения либо периода обращения показывает следующая формулы:
ω = 2 π / T = 2 π *f,
где:
- ω – угловая скорость в рад/с;
- T – период обращения;
- f – частота вращения.

Получить любую из этих трёх величин из другой можно с помощью правила пропорций, не забыв при этом перевести размерности в один формат (в минуты либо секунды)
Чему равна угловая скорость в конкретных случаях?
Приведём пример расчёта на основе приведённых выше формул. Допустим, имеется автомобиль. При движении на 100 км/ч его колесо, как показывает практика, делает в среднем 600 оборотов за минуту (f = 600 об/мин). Рассчитаем угловую скорость.
Для начала переведем об/мин в об/с. Для этого разделим 600 на 60 (число секунд в минуте) и получим 10 об/с . Попутно мы получили и период обращения: эта величина является обратной по отношению к частоте и при измерении в секундах 0,1 с.
Далее используем формулу:
ω = 2 π *f
Поскольку точно выразить π десятичными дробями невозможно, результат примерно равен будет 62,83 рад/с.
Связь угловой и линейной скоростей
На практике часто приходится проверять не только ту скорость, с какой изменяется угловое положение у вращающейся точки, но и скорость её самой применительно к линейному движению. В приведённом выше примере были сделаны расчёты для колеса – но колесо движется по дороге и либо вращается под действием скорости автомобиля, либо само ему эту скорость обеспечивает. Значит, каждая точка на поверхности колеса помимо угловой будет иметь и линейную скорость.
В приведённом выше примере были сделаны расчёты для колеса – но колесо движется по дороге и либо вращается под действием скорости автомобиля, либо само ему эту скорость обеспечивает. Значит, каждая точка на поверхности колеса помимо угловой будет иметь и линейную скорость.
Рассчитать её проще всего через радиус. Поскольку скорость зависит от времени (которым будет период обращения) и пройденного расстояния (которым является длина окружности), то, учитывая приведённые выше формулы, угловая и линейная скорость будут соотноситься так:
V = ωR
Где:
- V – линейная скорость;
- R – радиус.
Из формулы очевидно, что чем больше радиус, тем выше и значение такой скорости. Применительно к колесу с самой большой скоростью будет двигаться точка на внешней поверхности протектора (R максимален), но вот точно в центре ступицы линейная скорость будет равна нулю.
Ускорение, момент и связь их с массой
Помимо приведённых выше величин, с вращением связано ещё несколько моментов. Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.
Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.
Равномерное вращение – это важная вещь. Вот только нет ни одной детали, которая бы всё время крутилась равномерно. Число оборотов любого крутящегося узла, от коленвала до колеса, всегда в конечном итоге растёт, а затем падает. И та величина, которая показывает, насколько выросли обороты, называется угловым ускорением. Поскольку она производная от угловой скорости, измеряется она в радианах на секунду в квадрате (как линейное ускорение – в метрах на секунду в квадрате).
С движением и её изменением во времени связан и другой аспект – момент импульса. Если до этого момента мы могли рассматривать только чисто математические особенности движения, то здесь уже нужно учитывать то, что каждая деталь имеет массу, которая распределена вокруг оси. Он определяется соотношением начального положения точки с учётом направления движения – и импульса, то есть произведения массы на скорость.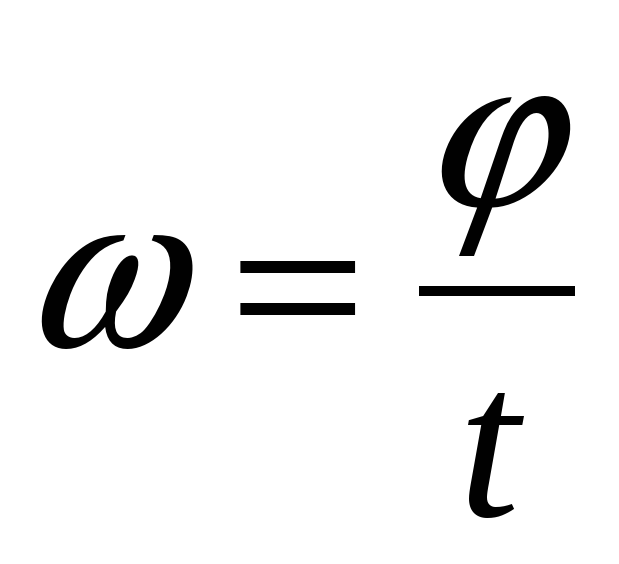 Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой
Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой
Шарнир как пример передачи импульса
Характерным примером того, как применяются все перечисленные выше данные, является шарнир равных угловых скоростей (ШРУС) . Эта деталь используется прежде всего на переднеприводных автомобилях, где важно не только обеспечить разный темп вращения колёс при повороте – но и при этом их управляемость и передачу на них импульса от работы двигателя.
ПОСМОТРЕТЬ ВИДЕО
Конструкция этого узла как раз и предназначена для того, чтобы:
- уравнивать между собой, как быстро вращаются колёса;
- обеспечивать вращение в момент поворота;
- гарантировать независимость задней подвеске.

В результате все формулы, приведённые выше, учитываются в работе ШРУС.
формула через радиус и ускорение, угловую скорость
Содержание:
-
Угловое ускорение – что это? -
Угловая скорость-
Основные формулы для вычисления угловой скорости -
Связь между угловой скоростью и нормальным (центростремительным) ускорением
-
-
Основные формулы для расчета углового ускорения-
Угловое ускорение маховика
-
-
Среднее угловое ускорение -
Тангенциальное ускорение -
Мгновенное угловое ускорение
Содержание
-
Угловое ускорение – что это? -
Угловая скорость-
Основные формулы для вычисления угловой скорости -
Связь между угловой скоростью и нормальным (центростремительным) ускорением
-
-
Основные формулы для расчета углового ускорения-
Угловое ускорение маховика
-
-
Среднее угловое ускорение -
Тангенциальное ускорение -
Мгновенное угловое ускорение
Угловое ускорение – что это?
Угловое ускорение \(\varepsilon\) – физическая величина, характеризующая изменение угловой скорости при движении тела. {-2}\)
{-2}\)
Угловая скорость
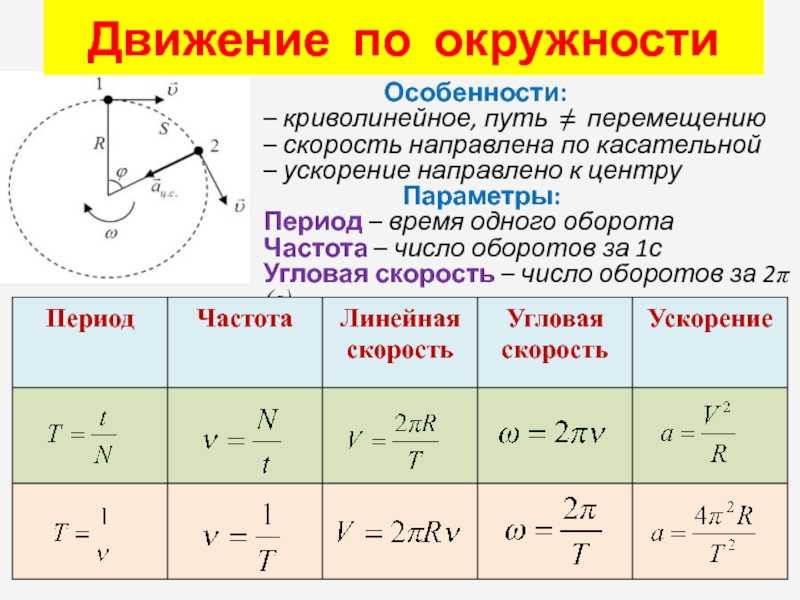
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
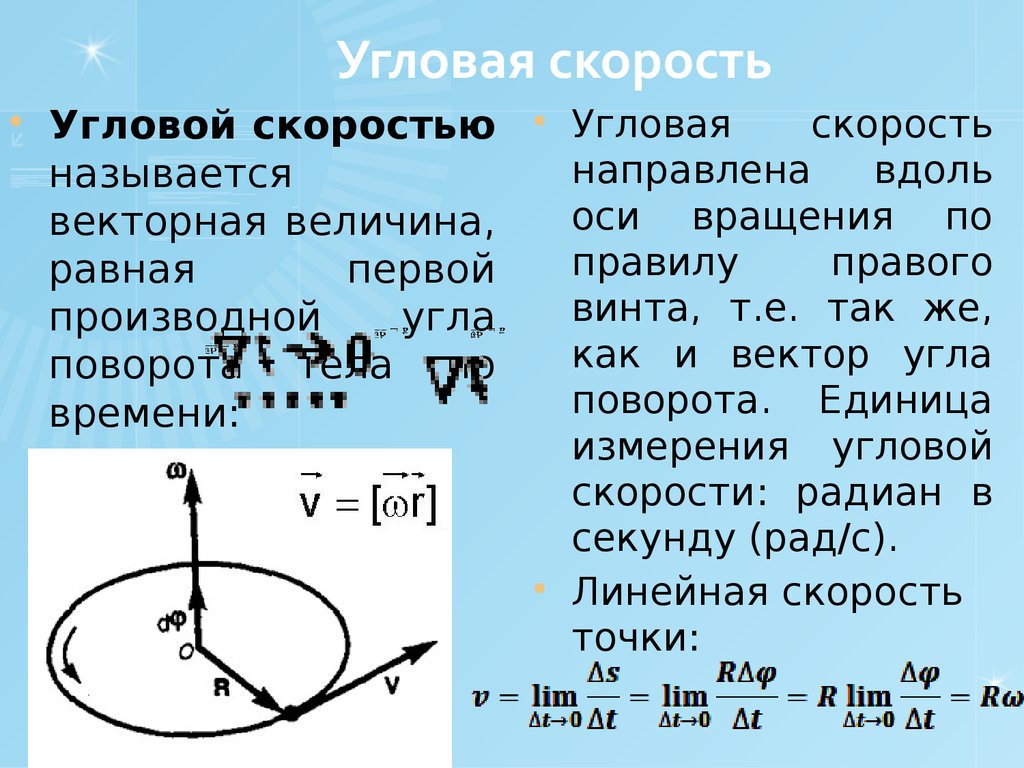
Угловая скорость \(\omega\) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- \(\omega=\frac nt\), где \(n\) – количество оборотов за единицу времени \(t\).
 2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)
2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)
Угловое ускорение маховика
\(\varepsilon=\frac\omega t=\frac{2\pi n}t\), где \(n\) – количество оборотов за единицу времени \(t\).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
\(\left\langle\varepsilon\right\rangle=\frac{\triangle\omega}{\triangle t}\)
Тангенциальное ускорение
Тангенциальным (касательным) ускорением \(a_\tau\) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.
\(a_\tau=\varepsilon r\), где \(\varepsilon\) – угловое ускорение, \(r\) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение \(\alpha\) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
 2}\)
2}\)
Насколько полезной была для вас статья?
Рейтинг: 2.30 (Голосов: 20)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Калькулятор угловой скорости
Создано Wojciech Sas, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 02 ноября 2022 г.
Содержание:
- Что такое угловая скорость?
- Формулы угловой скорости
- Единицы измерения угловой скорости
- Зависимость угловой скорости от угловой частоты
- Как найти угловую скорость Земли?
- Физические величины, зависящие от угловой скорости
- Сохранение углового момента
Этот калькулятор угловой скорости представляет собой простой в использовании инструмент, который дает немедленный ответ на вопрос « Как найти угловую скорость? «. В тексте вы найдете несколько формул угловой скорости , узнаете о различных единицах угловой скорости и, наконец, оцените угловую скорость Земли!
Задумывались ли вы когда-нибудь какова связь между угловой скоростью и угловой частотой или где применяется угловая скорость? Читайте дальше, чтобы узнать, и стать экспертом в области кругового движения.

🙋 Перейдите к нашему калькулятору кругового движения, чтобы также узнать о других важных величинах для вращающегося тела.
Что такое угловая скорость?
Угловая скорость описывает вращательное движение тел. Он измеряет, насколько быстро они движутся вокруг некоторого центра вращения. Мы можем думать о двух разных видах вращения. Первый описывает движение центра масс данного объекта вокруг определенной точки в пространстве , которую мы можем описать как начало координат. Некоторые примеры включают планеты, движущиеся вокруг Солнца, или автомобиль, съезжающий с шоссе.
Второй рассказывает о вращении тела вокруг собственного центра масс — спине (не путать с квантовым свойством частиц, также называемым спином). Наверняка вы видели, как баскетболист крутит мяч на пальце.
В целом можно сказать, что чем быстрее движение, тем выше угловая скорость. Мы должны перейти к уравнениям угловой скорости, описанным в следующем разделе, чтобы определить некоторые конкретные значения.

Формулы угловой скорости
Этот калькулятор угловой скорости использует две разные формулы угловой скорости в зависимости от ваших входных параметров.
Первое уравнение угловой скорости аналогично уравнению для линейной скорости:
ω = (α₂ - α₁) / t = Δα / t,где
α₁иα₁ 9005 круг, аΔα— их разность.t– время, за которое происходит изменение угла. Как видите, для нормальной скорости есть отношение смещения положения за период, а здесь мы используем угол вместо расстояния.Мы можем вывести вторую формулу угловой скорости из соотношения линейной скорости и радиуса, используя векторное произведение, которое равно:
v = ω × r.Мы можем переписать это выражение, чтобы получить уравнение угловой скорости:
ω = r × v / |r|²,где все эти переменные являются векторами , а
|r|обозначает абсолютное значение радиуса. Фактически угловая скорость представляет собой псевдовектор, направление которого перпендикулярно плоскости вращательного движения.
Фактически угловая скорость представляет собой псевдовектор, направление которого перпендикулярно плоскости вращательного движения.Единицы измерения угловой скорости
Существует несколько единиц измерения угловой скорости, и те, которые мы используем в нашем калькуляторе угловой скорости, перечислены ниже:
-
рад/сили радиан в секунду - Определение исходит прямо из первой формулы угловой скорости. Он показывает, насколько велик поворот (или угол), на который тело движется за заданное время, -
об/минили оборотов в минуту - Единица, наиболее часто встречающаяся в практическом применении. С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между10и100 RPM. -
Гцили герц - Те же единицы, которые используются для частоты, но редко используются в контексте угловой скорости. Это чем-то похоже на
Это чем-то похоже на об/мин, говорящее нам, сколько полных оборотов сделано за заданное время. Разница в том, что раньше основной единицей времени была минута, а здесь – секунда.
Естественно, все эти единицы угловой скорости пересчитываются между собой с использованием следующих соотношений:
1 RMP = 0,10472 рад/с = 0,01667 Гц,или наоборот:
,2 3 = рад /с = 60 об/мин.Угловая скорость в зависимости от угловой частоты
Посмотрите определение угловой частоты:
ω = 2·π·f,, где
f– частота. Как мы видим, он обозначается той же буквой. Кроме того, единицей угловой частоты являетсярад/с, точно так же, как и для угловой скорости. Поэтому может возникнуть вопрос: «Чем отличается угловая скорость от угловой частоты?».Ответ относительно прост. Связь между угловой частотой и угловой скоростью аналогична связи между скоростью и скоростью .
 Первое есть величина второго; другими словами, угловая частота является скаляром, тогда как угловая скорость является (псевдо)вектором.
Первое есть величина второго; другими словами, угловая частота является скаляром, тогда как угловая скорость является (псевдо)вектором.Мы обычно используем угловую частоту, когда говорим о гармоническом движении, примером которого является простой маятник. Как вы понимаете, движение не обязательно должно быть представлено стандартным вращением, а просто движением, которое периодически повторяет свое положение. Однако угловая скорость строго связана с движением вокруг некоторой точки. Следовательно, мы можем сказать, что угловая частота является более общей величиной, и мы можем использовать ее для описания широкого круга физических задач. Напротив, угловая скорость включает только вращательное движение.
🙋 У нас есть специальный инструмент, который объясняет, как рассчитать угловую частоту. Обязательно проверьте калькулятор угловой частоты!
Как найти угловую скорость Земли?
Как насчет того, чтобы воспользоваться нашим калькулятором угловой скорости? Оценим угловую скорость Земли! Во-первых, мы учитываем скорость вращения.
 Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за
Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с, что составляет примерно23,934 ч. Весь поворот составляет угол2π рад, поэтому результирующая угловая скорость равна:ω₁ = 2π рад / 23,934 ч = 0,2625 рад/ч = 0,00007292 рад/с /s(в экспоненциальном представлении).Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. Для этого нам нужен радиус Земли, примерно
6371 км. Нам осталось только подставить значения во вторую формулу угловой скорости:v₁ = r₁ · ω₁ = 6 371 км · 7,292·10⁻⁵ рад/с = 0,4646 км/с = 464,6 м/с.Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить этот результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно стартуют с космодромов, расположенных вблизи экватора, а не с полюсов? Ну, почти
500 м/сускорение в начале составляет значительную долю его конечной скорости. Таким образом, перемещение точки старта как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты.
Таким образом, перемещение точки старта как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты.После этого можно еще раз спросить, как найти угловую скорость Земли, но на этот раз орбитальную. Все расчеты аналогичны, но мы должны изменить время с
23,943 чна один год, что составляет около365,25дней. Изменение угла такое же, полный оборот.ω₂ = 2π рад / 23,934 ч = 0,0000001991 рад/с = 1,991·10⁻⁷ рад/с,и линейная скорость Земли относительно Солнца (для среднего радиуса
1,496·10⁸ км) равно:v₂ = 1,496·10⁸ км · 1,991·10⁻⁷ рад/с = 29,785 км/с.Мы движемся довольно быстро, не так ли?
Физические величины, зависящие от угловой скорости
Существует множество физических величин, связанных с угловой скоростью, некоторые из которых перечислены ниже:
-
Угловое ускорение - Описывает, как угловая скорость изменяется со временем.
 Чем выше разница угловых скоростей, тем больше значение углового ускорения. Не стесняйтесь проверить, как это работает на практике, с помощью нашего калькулятора углового ускорения.
Чем выше разница угловых скоростей, тем больше значение углового ускорения. Не стесняйтесь проверить, как это работает на практике, с помощью нашего калькулятора углового ускорения. -
Кинетическая энергия вращения - мера энергии при круговом движении. Как и в случае с кинетической энергией, зависимость (угловой) скорости является квадратичной.
-
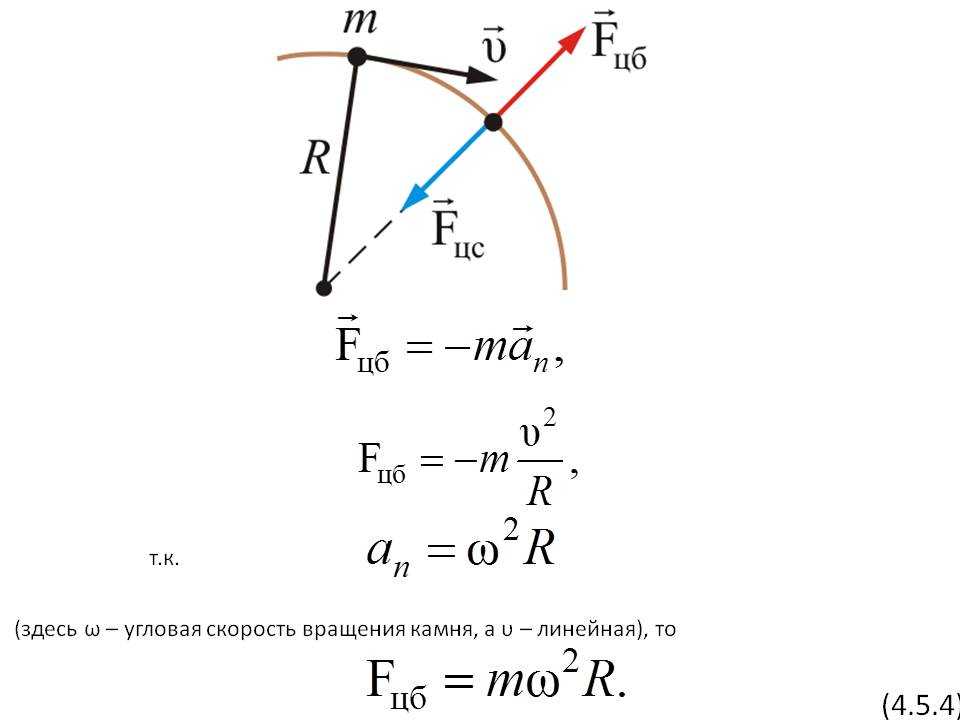
Центробежная сила. Ее можно почувствовать в машине, когда она поворачивается. Чем быстрее вы выполняете поворот или чем он круче, тем выше становится центробежная сила, которую мы отчетливо чувствуем.
-
Эффект Кориолиса. Это заставляет объекты вращаться, если они находятся на вращающемся теле (например, на Земле), а не двигаться по прямой линии.
-
Система шкивов - Это не физическая величина, точнее говоря, это интересное устройство, которое связано с угловой скоростью. Простейшая система состоит из двух шкивов, обычно с разными окружностями или радиусами. Их соединяет пояс, поэтому их линейные скорости одинаковы , но так как они разного размера, их угловые скорости изменяются пропорционально .
 Зная это и имея какой-нибудь двигатель с вполне определенной скоростью вращения, мы можем с хорошей точностью задавать угловую скорость выходного элемента, просто регулируя его размер.
Зная это и имея какой-нибудь двигатель с вполне определенной скоростью вращения, мы можем с хорошей точностью задавать угловую скорость выходного элемента, просто регулируя его размер.
Сохранение углового момента
Несколько фундаментальных правил говорят нам о величинах, сохраняющихся в изолированных системах. Наиболее известны законы сохранения энергии и сохранения импульса. Вместе с ними существует также сохранение момента количества движения . Если мы рассмотрим два момента времени, мы можем записать правило как:
I₁ · ω₁ = I₂ · ω₂,, где
I₁иI₂— начальный и конечный моменты инерции масс соответственно. , величины, описывающие распределение массы относительно центра тел.Мы видим, что при увеличении момента инерции угловая скорость уменьшается, и наоборот . Итак, каковы последствия этого явления? Представим, что вы фигурист. Когда вы вращаетесь, вы обладаете некоторой угловой скоростью.
 Если ваши руки широко раскрыты, момент инерции масс относительно велик . Затем вы приближаете руки к остальной части тела. Как следствие, ваш момент инерции уменьшается на , поэтому, поскольку общий угловой момент должен сохраняться, ваш угловая скорость увеличивается - значит крутиться будешь быстрее! Это не магия, просто физика!
Если ваши руки широко раскрыты, момент инерции масс относительно велик . Затем вы приближаете руки к остальной части тела. Как следствие, ваш момент инерции уменьшается на , поэтому, поскольку общий угловой момент должен сохраняться, ваш угловая скорость увеличивается - значит крутиться будешь быстрее! Это не магия, просто физика!Если вам не нравится кататься на коньках, можно попробовать проверить правило на обычном вращающемся стуле. Просто помните, безопасность превыше всего! Убедитесь, что есть достаточно места для проведения этого эксперимента. После этого просто начните вращаться и посмотрите, как изменится ваша угловая скорость, когда вы двигаете руками вперед и назад. Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете совместить и тренировки, и развлечения в одно целое!
Wojciech Sas, PhD
#1 Угловая разность
Изменение угла (Δα)
Время (t)
Угловая скорость (ω)
#2 Радиальная скорость
)
Скорость (
) Скорость (
)
Угловая скорость (ω)
Посмотрите 20 похожих калькуляторов вращательного и периодического движения 🌎
Угловое ускорениеУгловое смещениеУгловая частота… Еще 17
Формула угловой скорости - GeeksforGeeks
Средняя угловая скорость определяется как отношение углового смещения ко времени, затраченному объектом на смещение.
 Обозначается ω av .
Обозначается ω av .ω AV = угловое смещение / перемещение во времени
Рассмотрим движение частицы на круговой пути с центром в O.
. Предположим, что во время ΔT DESPLACE под углом Δθ .
тогда средняя угловая скорость ω av = Δθ/ Δt
Поскольку Δθ является скалярной величиной, средняя угловая скорость является скалярной величиной.
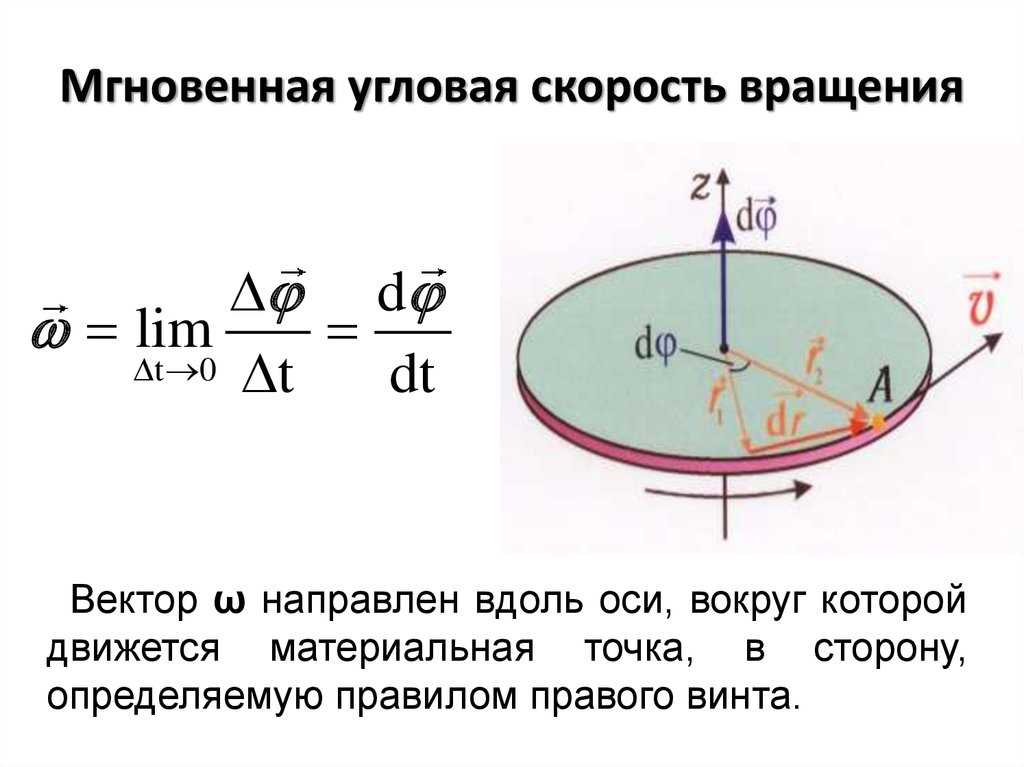
Мгновенная угловая скорость
Это предельное значение средней угловой скорости объекта в малом интервале времени, когда интервал времени приближается к нулю. Обозначается ω.
ω = Lt t -> 0 Δθ/ Δt = dθ/dt
Угловая скорость измеряется в радианах в секунду, и ее единица измерения составляет рад/с.
Поскольку dθ является вектором, ω также является вектором.

Связь между угловой скоростью и линейной скоростью.
Линейная скорость представляет собой векторное произведение угловой скорости и радиуса кругового пути.
v = ω x r
где,
v = линейная скорость,
ω = угловая скорость &
r = вектор положения от центра кругового пути (радиус).
Термины период времени и частота являются синонимами угловой скорости, поэтому их необходимо определять вместе с угловой скоростью.
Период времени
Время, необходимое для совершения одного оборота или смещения на угол 2π радиан, называется периодом времени и обозначается T .
, так как угловая скорость ω равна угловому смещению/времени, следовательно, период времени связан с угловой скоростью как
ω = 2π/ T
T = 2π/ω
Частота
Частота
Число оборотов объекта в секунду.
 Обозначается греческой буквой nu ( ν ).
Обозначается греческой буквой nu ( ν ).ν = 1/T = ω/2π
Примеры задач
Задача 1. Вычислить угловую скорость минутной стрелки часов.
Минутная стрелка совершает один оборот за 60 минут.
=> смещается на 2π радиан за 60*60 секунд
=> ω = 2π/3600 = 1,74 * 10 -3 рад/сек.
Задача 2. Шарик вращается по окружности диаметром 4 м со скоростью 20 м/с. Найдите его угловую скорость.
радиус окружности = диаметр/2 = 4/2 = 2 м
линейная скорость = 20 м/с
угловая скорость = v / r
ω = 20 / 2 = 10 рад/с
Задача 3: Объект вращается по горизонтальной окружности радиусом 12 м с частотой 4 Гц. Найдите его линейную скорость.
Линейная скорость v = ω * r
частота (f) = ω/2π
=> ω = 2π * f
=> v = 2π * f * r
=> v = 301,59 м/59 с.

 2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)
2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)
 2}\)
2}\)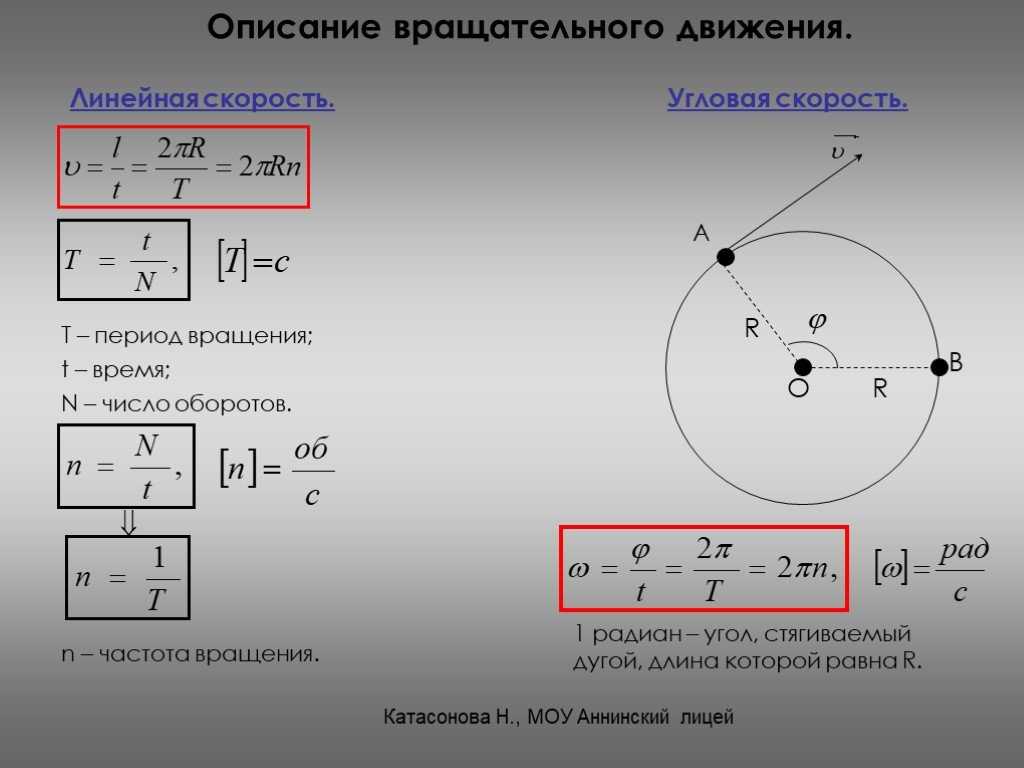
 Фактически угловая скорость представляет собой псевдовектор, направление которого перпендикулярно плоскости вращательного движения.
Фактически угловая скорость представляет собой псевдовектор, направление которого перпендикулярно плоскости вращательного движения. Это чем-то похоже на
Это чем-то похоже на  Первое есть величина второго; другими словами, угловая частота является скаляром, тогда как угловая скорость является (псевдо)вектором.
Первое есть величина второго; другими словами, угловая частота является скаляром, тогда как угловая скорость является (псевдо)вектором. Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за
Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за  Таким образом, перемещение точки старта как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты.
Таким образом, перемещение точки старта как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты. Чем выше разница угловых скоростей, тем больше значение углового ускорения. Не стесняйтесь проверить, как это работает на практике, с помощью нашего калькулятора углового ускорения.
Чем выше разница угловых скоростей, тем больше значение углового ускорения. Не стесняйтесь проверить, как это работает на практике, с помощью нашего калькулятора углового ускорения. Зная это и имея какой-нибудь двигатель с вполне определенной скоростью вращения, мы можем с хорошей точностью задавать угловую скорость выходного элемента, просто регулируя его размер.
Зная это и имея какой-нибудь двигатель с вполне определенной скоростью вращения, мы можем с хорошей точностью задавать угловую скорость выходного элемента, просто регулируя его размер.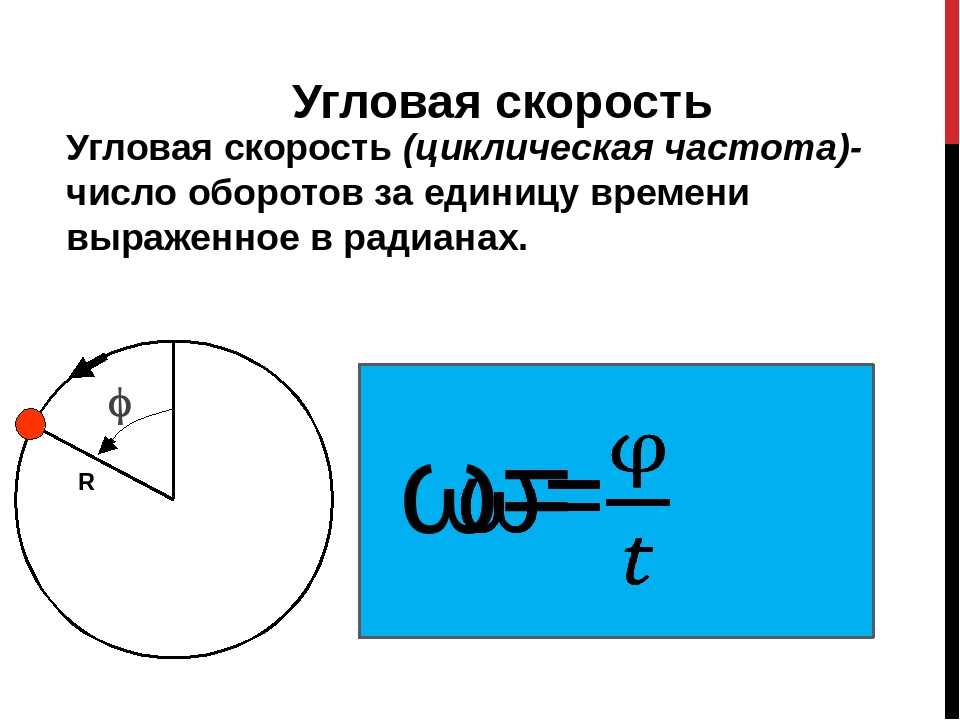 Если ваши руки широко раскрыты, момент инерции масс относительно велик . Затем вы приближаете руки к остальной части тела. Как следствие, ваш момент инерции уменьшается на , поэтому, поскольку общий угловой момент должен сохраняться, ваш угловая скорость увеличивается - значит крутиться будешь быстрее! Это не магия, просто физика!
Если ваши руки широко раскрыты, момент инерции масс относительно велик . Затем вы приближаете руки к остальной части тела. Как следствие, ваш момент инерции уменьшается на , поэтому, поскольку общий угловой момент должен сохраняться, ваш угловая скорость увеличивается - значит крутиться будешь быстрее! Это не магия, просто физика! Обозначается ω av .
Обозначается ω av .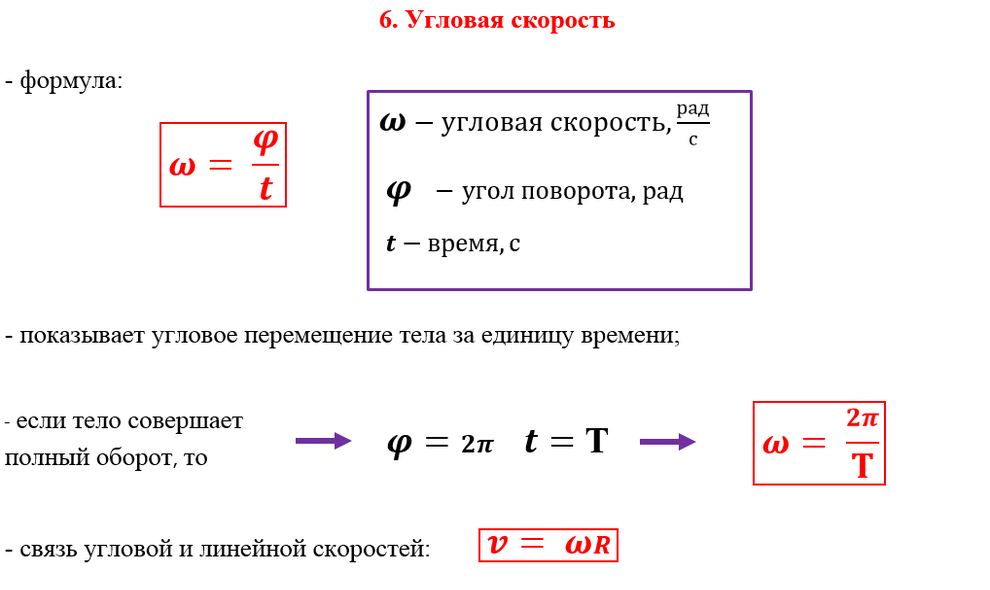
 Обозначается греческой буквой nu ( ν ).
Обозначается греческой буквой nu ( ν ).