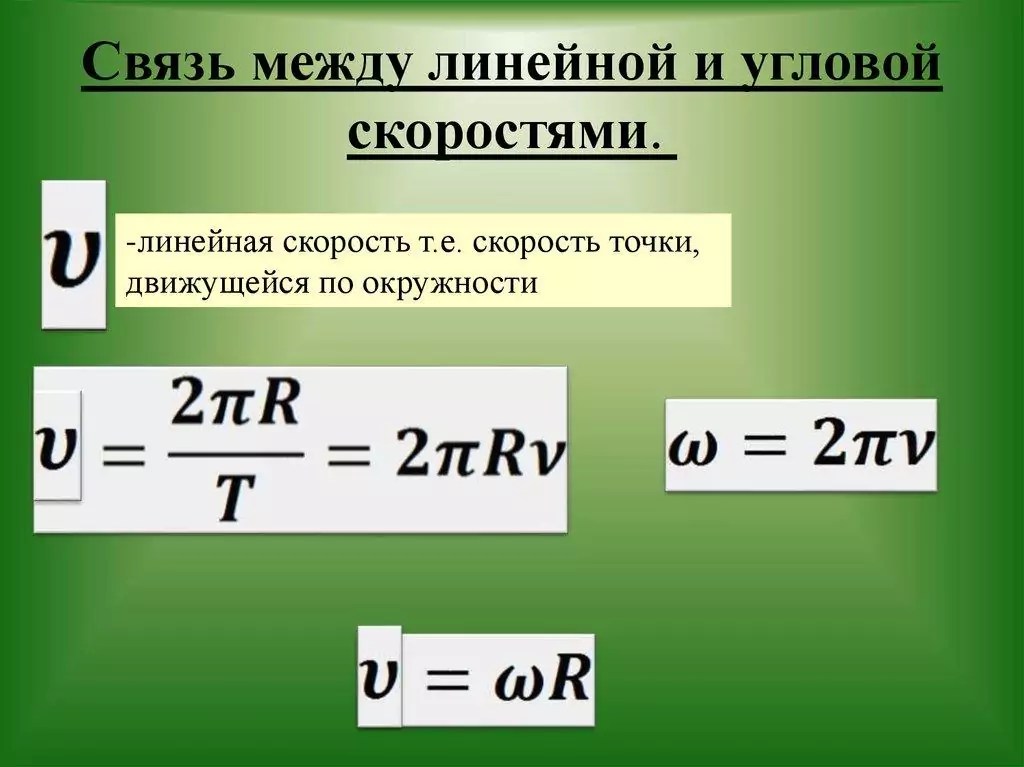
Содержание
Угловая скорость
Положение материальной точки на окружности определяется радиусом-вектором $ \overrightarrow {r}$, проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).
Рисунок 1. Радиус-вектор, перемещение, путь и угол поворота при движении точки по окружности
При этом движение тела по окружности можно однозначно описать с помощью таких кинематических характеристик, как угол поворота, угловая скорость и угловое ускорение.
За время ∆t тело, двигаясь из точки А в точку В, совершает перемещение $\triangle r$, равное хорде АВ, и проходит путь, равный длине дуги l. Радиус-вектор поворачивается на угол ∆$ \varphi $.
Угол поворота можно характеризовать вектором углового перемещения $d\overrightarrow{{\mathbf \varphi }}$, модуль которого равен углу поворота ∆$ \varphi $, а направление совпадает с осью вращения, причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора $d\overrightarrow{{\mathbf \varphi }}$.
Вектор $d\overrightarrow{{\mathbf \varphi }}$ называется аксиальным вектором (или псевдо-вектором), тогда как вектор перемещения $\triangle \overrightarrow{r}$ является полярным вектором (к ним также относятся векторы скорости и ускорения). Они отличаются тем, что полярный вектор кроме длины и направления имеет точку приложения (полюс), а аксиальный вектор имеет только длину и направление (ось — по латыни axis), но не имеет точки приложения. Векторы такого типа часто применяются в физике. К ним, например, относятся все вектора, являющиеся векторным произведением двух полярных векторов.
Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется средней угловой скоростью: $\left\langle \omega \right\rangle =\frac{\triangle \varphi }{\triangle t}$. В СИ единицей угловой скорости является радиан в секунду $( \frac {рад} {c})$.
Определение
Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
\[\overrightarrow{{\mathbf \omega }}\left(t\right)={\mathop{lim}_{\triangle t\to 0} \frac{\triangle {\mathbf \varphi }}{\triangle t}=\frac{d\overrightarrow{{\mathbf \varphi }}}{dt}\ }\]
При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ${\mathbf \omega }=const$; $v=const$. 2R$
2R$
При неравномерном движении по окружности вектор угловой скорости является векторной функцией от времени $\overrightarrow{\omega }\left(t\right)={\overrightarrow{\omega }}_0+\overrightarrow{\varepsilon }\left(t\right)t$, где ${\overrightarrow{{\mathbf \omega }}}_0$ — начальная угловая скорость, $\overrightarrow{{\mathbf \varepsilon }}\left(t\right)$ — угловое ускорение. В случае равнопеременного движения, $\left|\overrightarrow{{\mathbf \varepsilon }}\left(t\right)\right|=\varepsilon =const$, и $\left|\overrightarrow{{\mathbf \omega }}\left(t\right)\right|=\omega \left(t\right)={\omega }_0+\varepsilon t$.
Задача 1
Опишите движение вращающегося твердого тела в случаях, когда угловая скорость изменяется согласно графикам 1 и 2, изображенным на рис.2.
Рисунок 2.
Решение
Вращение бывает в двух направлениях — по часовой стрелке и против. С направлением вращения связан псевдовектор угла поворота и угловой скорости.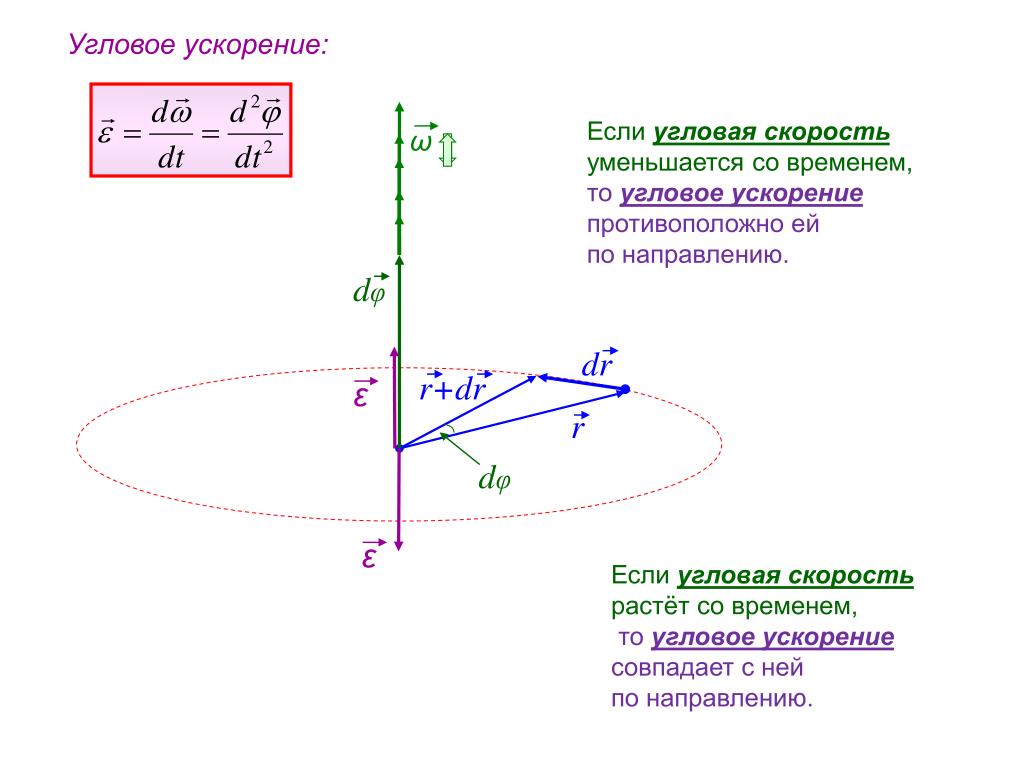 Пусть положительным будем считать направление вращения по часовой стрелке.
Пусть положительным будем считать направление вращения по часовой стрелке.
Для движения 1 угловая скорость возрастает, но угловое ускорение $\varepsilon $=d$\omega $/dt (производная) уменьшается, оставаясь положительным. Следовательно, это движение является ускоренным по часовой стрелке с уменьшающимся по величине ускорением.
Для движения 2 угловая скорость уменьшается, затем достигает в точке пересечения с осью абсцисс нуля, а далее становится отрицательной и возрастает по модулю. Угловое ускорение отрицательно и уменьшается по модулю. Таким образом, сначала точка двигалась по часовой стрелке замедленно с уменьшающимся по модулю угловым ускорением, остановилась и стала вращаться ускоренно с уменьшающимся по модулю ускорением.
Задача 2
Найти радиус R вращающегося колеса, если известно, что линейная скорость $v_1$ точки, лежащей на ободе, в 2,5 раза больше линейной скорости $v_2$ точки, лежащей на расстоянии $r = 5 см$ ближе к оси колеса.
Решение
Рисунок 3.
Дано:
$$R_2 = R_1 — 5$$
$$v_1 = 2,5v_2$$
$$R_1 = ?$$
Точки движутся по концентрическим окружностям, вектора их угловых скоростей равны, $\left|{\overrightarrow{\omega }}_1\right|=\left|{\overrightarrow{\omega }}_2\right|=\omega $ , следовательно, можно записать в скалярной форме:
\[v_1=\omega R_1; v_2=\omega R_2;\frac{v_1}{v_2}=\frac{\omega R_1}{\omega R_2}=\frac{R_1}{R_1-5}=2,5;;\ R_1=\frac{5\times 2,5}{1.5}=8,3\ см\ \ \]
Ответ: радиус колеса R = 8,3 см
Сообщество экспертов Автор24
Автор этой статьи
Дата последнего обновления статьи: 17.11.2021
Выполнение любых типов работ по
физике
Онлайн помощь по физике
Заказать решение задач по термодинамике
Отчет по практике по физике
Контрольная работа по теме кинематика
Презентация на тему термодинамика
Реферат на тему термодинамика
Контрольная работа на тему термодинамика
Контрольная работа по физике на тему термодинамика
Презентация на тему физика атомного ядра
Презентация на тему атомная физика
Подбор готовых материалов по теме
Дипломные работы
Курсовые работы
Выпускные квалификационные работы
Рефераты
Сочинения
Доклады
Эссе
Отчеты по практике
Решения задач
Контрольные работы
1.
 4 Угловая скорость и угловое ускорение
4 Угловая скорость и угловое ускорение
Рассмотрим
твердое тело, которое вращается вокруг
неподвижной оси. Тогда отдельные точки
этого тела будут описывать окружности
разных радиусов, центры которых лежат
на оси вращения. Пусть некоторая
точка движется по окружности радиуса
R
(рис.6). Ее положение через промежуток
времени Δ t
зададим углом .
Элементарные (бесконечно малые) углы
поворота рассматриваются как векторы.
Модуль вектора dφ
равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется
правилу
правого винта
(рис.6).
|
Рис. |
Векторы, |
Угловой
скоростью
называется векторная величина, равная
первой производной угла поворота тела
по времени:
Вектор
направлен вдоль оси вращения по правилу
правого винта, т.е. так же, как и вектор(рис.7).
В векторном виде
формулу для линейной скорости можно
написать как векторное произведение:
.
|
Рис. |
Размерность т.е. v=R. |
Если
=const,
то вращение равномерное и его можно
характеризовать периодом
вращения
Т – временем, за которое точка
совершает один полный оборот, т.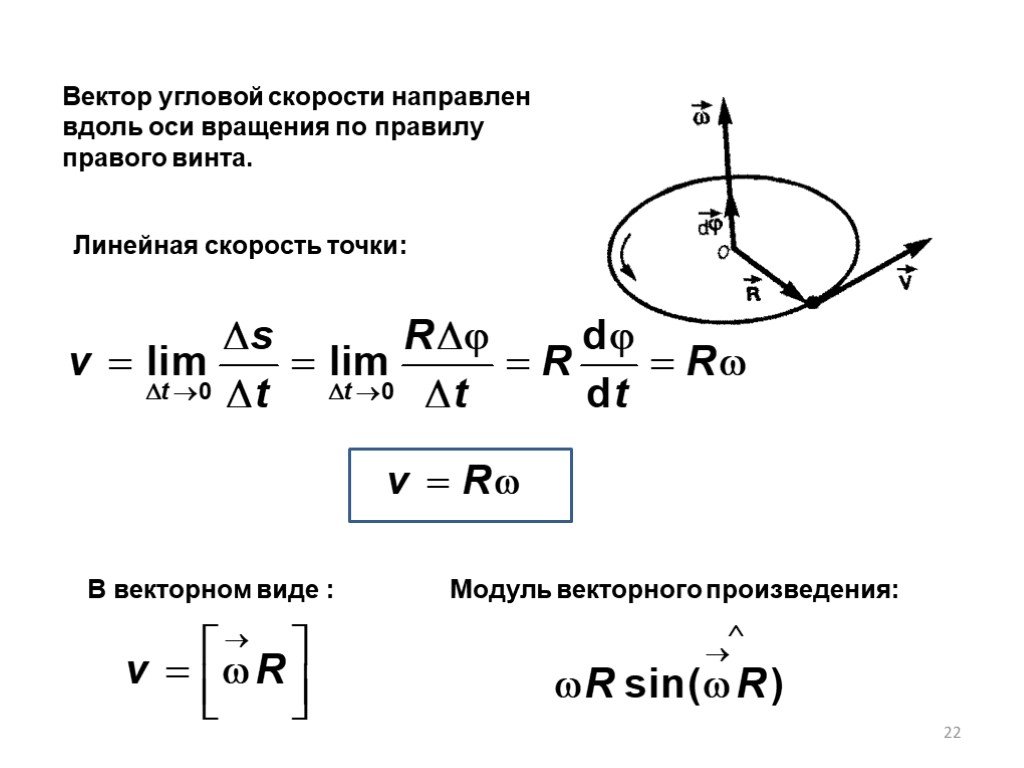 е.
е.
поворачивается на угол 2
.Так
как промежуток времени Δt=Т
соответствует
,
то,
откуда
Число
полных оборотов, совершаемых телом при
равномерном его
движении по окружности
в единицу времени, называется частотой
вращения
,
откуда
Угловым
ускорением
называется векторная величина, равная
первой производной угловой скоростипо времени:
.
При
вращении тела вокруг неподвижной оси
вектор углового ускорения направлен
вдоль оси вращения в сторону вектора
элементарного приращения угловой
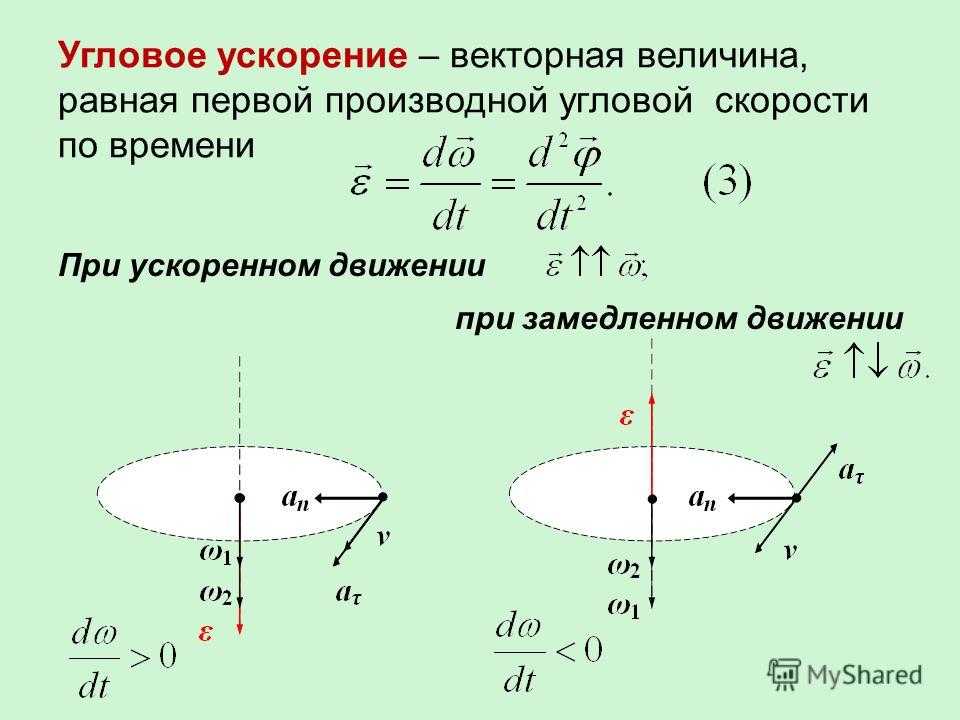
скорости. При ускоренном движении
вектор
сонаправлен
вектору
(рис. 8), при замедленном — противонаправлен
ему (рис.9).
Тангенциальная
составляющая ускорения
и
.
Нормальная
составляющая ускорения
Таким
образом, связь между линейными (длина
пути s,
пройденного точкой по дуге окружности
радиуса R,
линейная скорость
,
тангенциальное ускорение а, нормальное
ускорение аn)
и угловыми величинами (угол поворота
,
угловая скорость ,
угловое ускорение )
выражается следующими формулами:
s=Rφ,
=R,
ат=R,
аn=2R.
В
случае равнопеременного движения точки
по окружности (=const):
=o
±t,
,
где0
—
начальная угловая скорость.
2. Динамика материальной точки и поступательного движения твердого тела
2.1. Первый закон Ньютона. Масса. Сила
Динамика
является основным разделом механики,
в ее основе лежат три закона Ньютона,
сформулированные им в 1687 г. Законы
Ньютона играют исключительную роль
в механике и являются (как и все физические
законы) обобщением результатов всего
человеческого опыта.
Первый
закон Ньютона:
всякая материальная точка (тело)
сохраняет состояние покоя или
равномерного прямолинейного движения
до тех пор, пока воздействие со стороны
других тел не заставит ее изменить
это состояние.
Стремление
сохранять состояние покоя или равномерного
прямолинейного движения называется
инертностью.
Поэтому первый закон Ньютона называют
также законом
инерции.
Механическое
движение относительно, и его характер
зависит от системы отсчета. Первый закон
Ньютона выполняется не во всякой системе
отсчета, а те системы, по отношению, к
которым он выполняется, называются
инерциальными
системами отсчета.
Инерциальной системой отсчета является
такая система, которая либо покоится,
либо движется равномерно и прямолинейно
относительно какой-то другой
инерциальной системы. Первый закон
Ньютона утверждает существование
инерциальных систем отсчета.
Опытным
путем установлено, что инерциальной
можно считать гелиоцентрическую
(звездную) систему отсчета (начало
координат находится в центре Солнца,
а оси проведены в направлении определенных
звезд). Система отсчета, связанная с
Землей, строго говоря, неинерциальна,
однако эффекты, обусловленные ее
неинерциальностью (Земля вращается
вокруг собственной оси и вокруг Солнца),
при решении многих задач пренебрежимо
малы, и в этих случаях ее можно считать
инерциальной .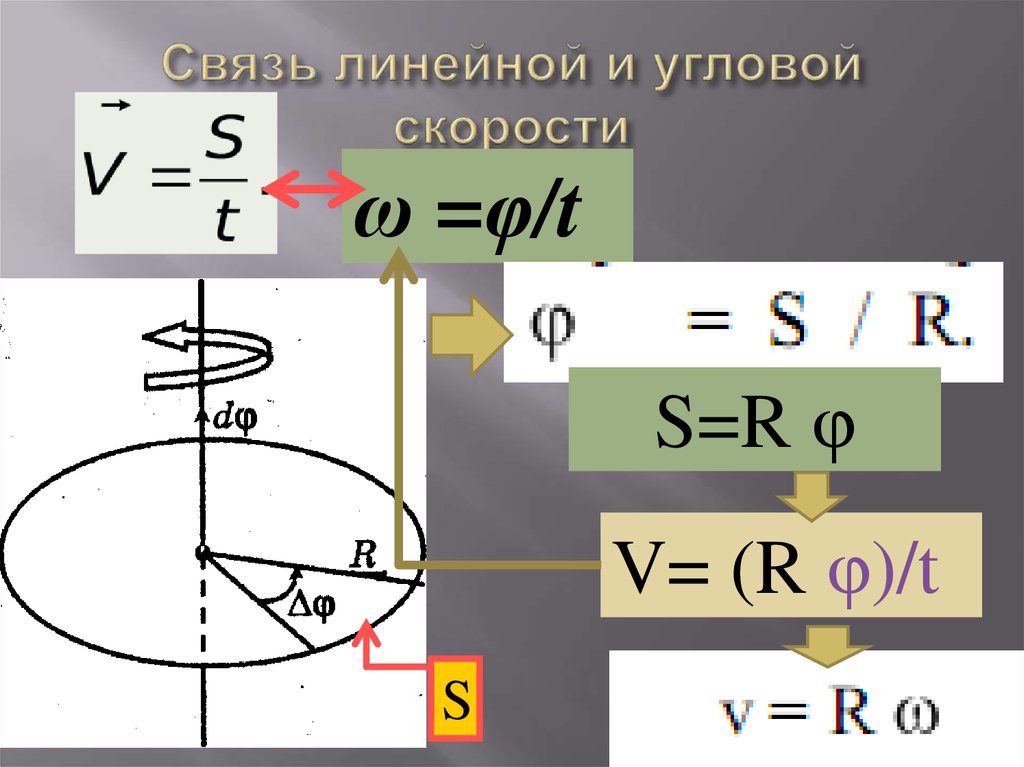 Из опыта известно, что
Из опыта известно, что
при одинаковых воздействиях различные
тела неодинаково изменяют скорость
своего движения, т.е., иными словами,
приобретают различные ускорения.
Ускорение зависит не только от
величины воздействия, но и от свойств
самого тела (от его массы). Масса
тела — физическая величина, являющаяся
одной из основных характеристик
материи, определяющая ее инерционные
и гравитационные свойства.
В
настоящее время можно считать доказанным,
что инертная и гравитационная массы
равны друг другу (с точностью, не меньшей
10-12
их значения).
Чтобы
описать воздействия, упоминаемые в
первом законе Ньютона, вводят понятие
силы. Под действием сил тела либо изменяют
скорость движения, т.е. приобретают
ускорения, либо деформируются, т.е.
изменяют свою форму и размеры. В каждый
момент времени сила характеризуется
числовым значением, направлением в
пространстве и точкой приложения. Итак,
сила
— это векторная величина, являющаяся
мерой механического воздействия на
тело со стороны других тел или полей, в
результате, которого тело приобретает
ускорение или изменяет свою форму и
размеры.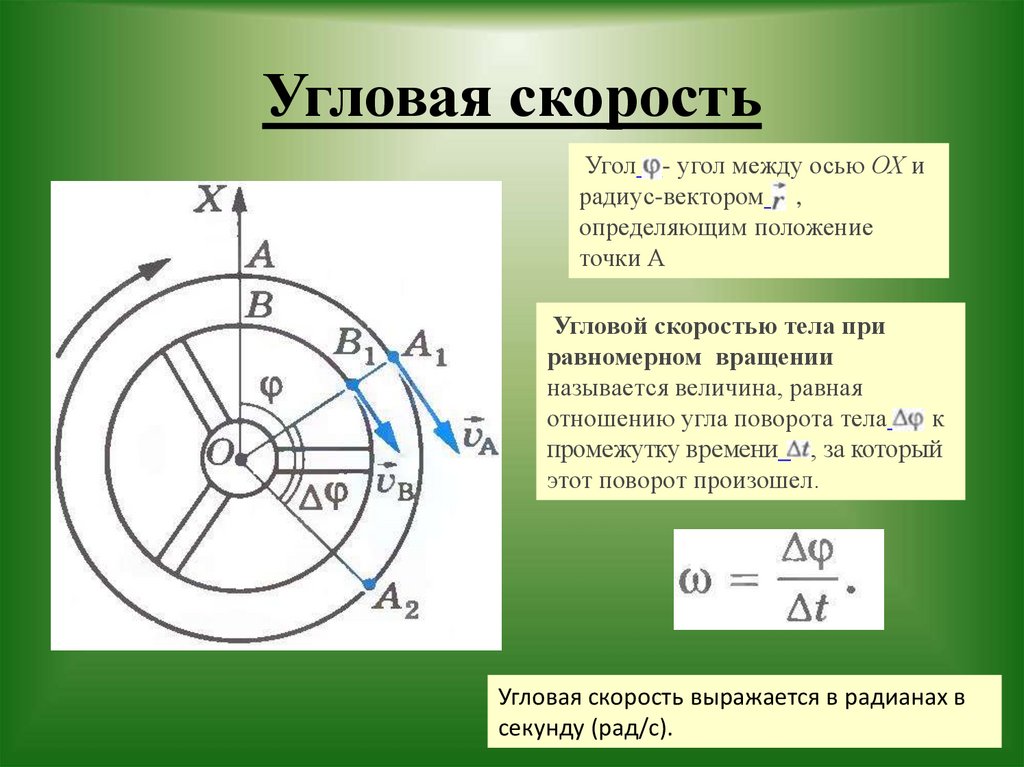
Количество оборотов
Количество оборотов
Стандартный угол направленной величины принимается равным против часовой стрелки от положительной оси x. |
Индекс
Центростремительное ускорение |
|||||||||||||||||||||||||||||||||||||||||||||||||
2
6.1 Угол вращения и угловая скорость — College Physics 2eЦели обученияК концу этого раздела вы сможете:
В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения. Угол поворотаКогда объекты вращаются вокруг некоторой оси — например, когда CD (компакт-диск) на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по дуге окружности. Рассмотрим линию от центра компакт-диска к его краю. Каждая яма, используемая для записи звука вдоль этой линии, проходит под одним и тем же углом за одно и то же время. Угол поворота представляет собой величину поворота и аналогичен линейному расстоянию. Δθ=Δср.Δθ=Δср. 6.1 Рисунок Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt. Рисунок Радиус окружности повернут на угол ΔθΔθ. Длина дуги ΔsΔs описана на окружности. Длина дуги ΔsΔs — это расстояние, пройденное по круговому пути, как показано на рис. 6.3. Обратите внимание, что rr — это радиус кривизны кругового пути. Мы знаем, что для одного полного оборота длина дуги равна длине окружности радиуса rr. Длина окружности равна 2πr2πr. Таким образом, за один полный оборот угол поворота равен . Δθ=2πrr=2π.Δθ=2πrr=2π. 6.2 Этот результат является основой для определения единиц, используемых для измерения углов поворота, ΔθΔθ – радианы (рад), определенные таким образом, что 2πрад = 1 оборот. 6.3 Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 6.1.
Стол Сравнение угловых единиц Рисунок Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги ΔsΔs, поскольку она находится на большем расстоянии от центра вращения (r)(r). Если Δθ=2πΔθ=2π рад, то компакт-диск совершил один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку существует 360º360º по кругу или одной революции, взаимосвязь между радианами и градусами, таким образом, 2πrad = 360º2πrad = 360º 6,4 , так что 1RAD = 360º2π поездки 3º.1rad = 360º2πt. 6,5 Угловая скоростьКак быстро вращается объект? Мы определяем угловую скорость ωω как скорость изменения угла. В символах это ω=ΔθΔt,ω=ΔθΔt, 6.6 где угловой поворот ΔθΔθ происходит за время ΔtΔt. Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Угловая скорость ωω аналогична линейной скорости vv. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске. Эта яма перемещается на длину дуги ΔsΔs за время ΔtΔt, поэтому она имеет линейную скорость v=ΔsΔt.v=ΔsΔt. 6,7 Из Δθ=ΔsrΔθ=Δsr мы видим, что Δs=rΔθΔs=rΔθ. Подстановка этого в выражение для vv дает v=rΔθΔt=rω.v=rΔθΔt=rω. 6,8 Мы запишем это отношение двумя разными способами и получим два разных понимания: v=rω или ω=vr.v=rω или ω=vr. 6,9 Первое соотношение в v=rω или ω=vrv=rω или ω=vr утверждает, что линейная скорость vv пропорциональна расстоянию от центра вращения, поэтому она наибольшая для точки на ободе (самый большой rr), как и следовало ожидать. Мы также можем назвать эту линейную скорость vv точки на ободе тангенциальная скорость . Рисунок Автомобиль, движущийся со скоростью vv вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси равна vv, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v=rωv=rω, где rr — радиус шины. Большая угловая скорость шины означает большую скорость автомобиля. Пример
|

 Средние значения скорости и ускорения определяются соотношениями:
Средние значения скорости и ускорения определяются соотношениями: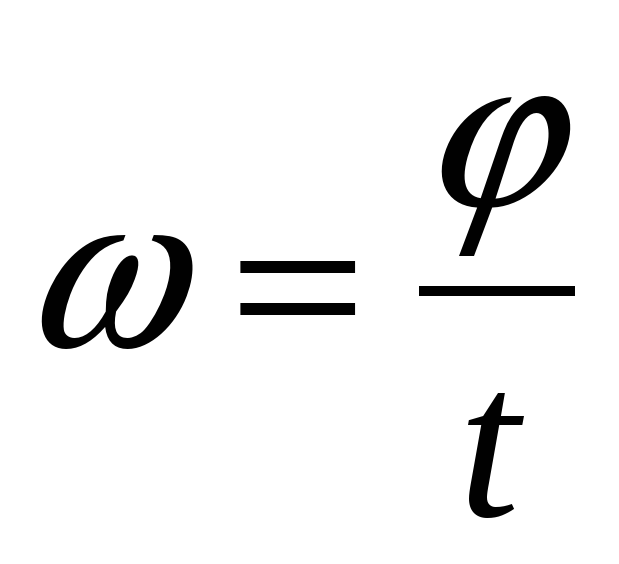

 Определим угол поворота ΔθΔθ как отношение длины дуги к радиусу кривизны:
Определим угол поворота ΔθΔθ как отношение длины дуги к радиусу кривизны: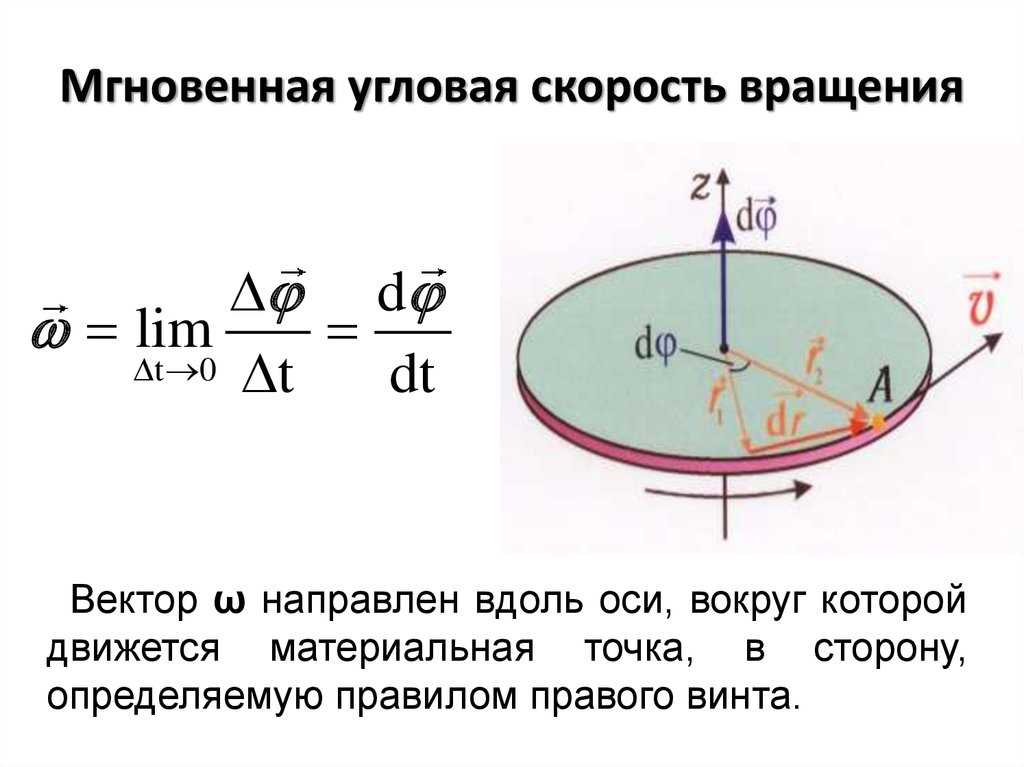 2πрад = 1 оборот.
2πрад = 1 оборот.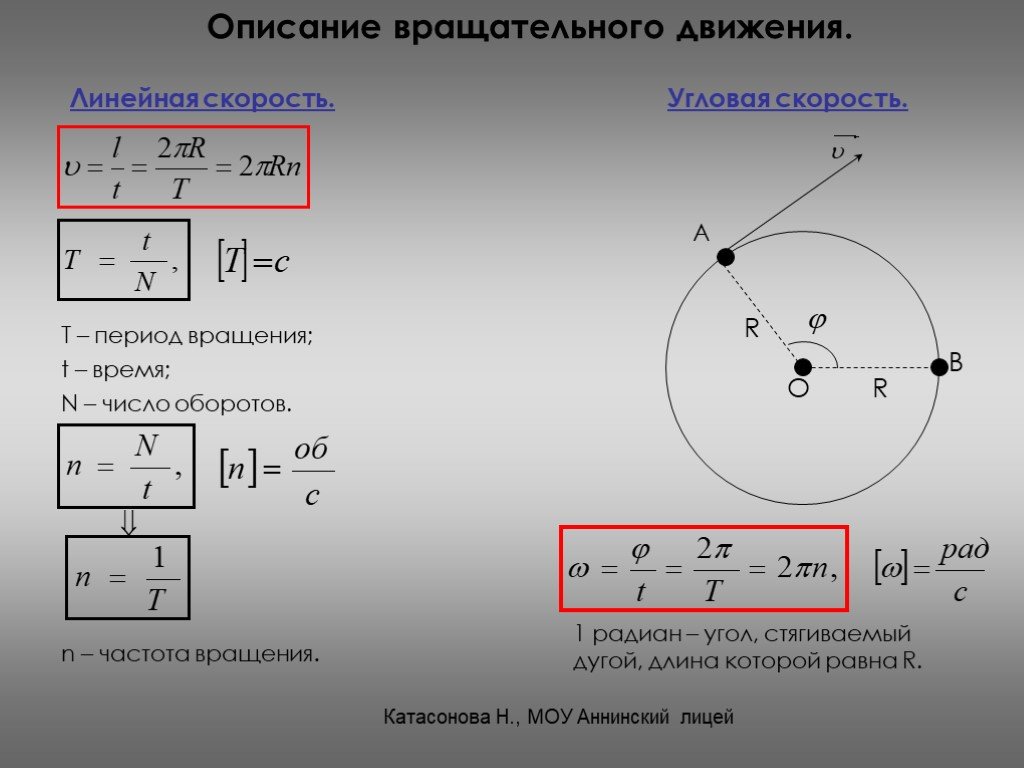 Второе соотношение в v=rω или ω=vrv=rω или ω=vr можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости vv автомобиля. См. рисунок 6.5. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большое vv означает большое ωω, потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω), будет производить большую линейную скорость (vv) автомобиля.
Второе соотношение в v=rω или ω=vrv=rω или ω=vr можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости vv автомобиля. См. рисунок 6.5. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большое vv означает большое ωω, потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ωω), будет производить большую линейную скорость (vv) автомобиля. См. рисунок 6.5.
См. рисунок 6.5. Они будут иметь угловую скорость
Они будут иметь угловую скорость