Содержание
Поступательное и вращательное движение твёрдого тела: определение, скорость, ускорение
Физика
12.11.21
14 мин.
При изменении положения физической точки относительно выбранной системы говорят о выполнении механического перемещения. Существуют разнообразные способы его совершения. Одним из них является поступательное движение твёрдого тела. Вращательное перемещение интересно тем, что размерами объекта пренебречь нельзя. Значит, в описании процесса нужно использовать дополнительные величины, которые требуют понимания и изучения.
Оглавление:
- Общие сведения
- Период и частота
- Линейная и угловая скорость
- Ускорение движения
Общие сведения
Механическим движением называют изменение положения тела относительно других объектов с течением времени. Например, езда на велосипеде, полёт мяча, бег спортсмена. При рассматривании таких процессов формы тел не учитываются. Это связано с тем, что их размеры по сравнению с пройденным расстоянием не имеют значения. Для таких случаев вводится понятие — материальная точка. То есть объекта, размерами которого можно пренебречь.
При рассматривании таких процессов формы тел не учитываются. Это связано с тем, что их размеры по сравнению с пройденным расстоянием не имеют значения. Для таких случаев вводится понятие — материальная точка. То есть объекта, размерами которого можно пренебречь.
Описывают механическое движение с помощью трёх простейших величин:
- пути;
- скорости;
- времени перемещения.
Пусть имеется некое объёмное тело, например, книга. Если её взять и помахать ею в пространстве, то, можно сказать, что точки из которых она состоит движутся по-разному. Они имеют разную скорость, проходят различный путь. Следовательно, описать движение такого тела сложно. Именно поэтому вводят понятие материальной точки.
Но бывают такие ситуации, когда объект проходит путь, соизмеримый с размерами самого тела. В этом случае принимать его за точку нельзя. Можно представить, что предмет движется по дуге. Тогда скорости точек, из которых он состоит будут одинаковыми.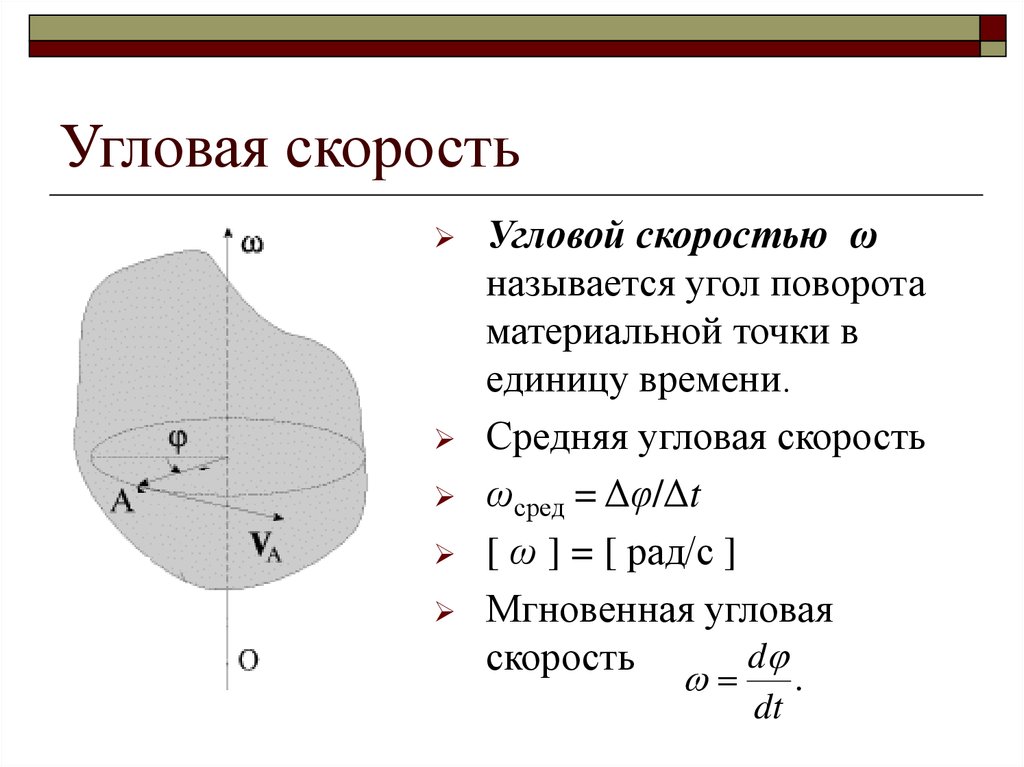 Равным окажется и пройденный ими путь. Этот простейший вид движения называют поступательным. Другими словами, перемещением, при котором все его точки движутся одинаково.
Равным окажется и пройденный ими путь. Этот простейший вид движения называют поступательным. Другими словами, перемещением, при котором все его точки движутся одинаково.
Частным случаем такого изменения положения является вращательное движение. Из наиболее яркого примера можно привести вращение колеса. Рассматривая его, нужно отметить, что точки, расположенные ближе к центру, будут проходить меньшее расстояние, чем те, что находятся возле обода. Значит, и их скорости будут разными, поэтому в этом случае нужно учитывать размеры тела.
Так как для описания процесса использовать материальную точку нельзя, то и рассматривать движение с помощью скорости и расстояния будет неудобно и очень сложно. Вот почему изучают не траектории отдельных величин, а углы, на которые поворачиваются радиусы, количество оборотов. Следует отметить, что при вращательном движении все точки тела движутся по окружности, центры лежат на одной прямой. Называется она — осью.
Таким образом, под вращательным движением понимают такое изменение положение в пространстве, при котором все его точки перемещаются по окружностям с центрами, лежащими на одной прямой.
При этом происходит этот процесс за время t.
Период и частота
Пусть имеется тело цилиндрической формы. На нём можно выделить две точки: A и B. Они вращаются по окружности с разным радиусом. Первая расположена ближе к центру, значит, длина её траектории будет меньше, чем второй. Центры их движения лежат на одной прямой — оси вращения, проходящей через точку O.
За одно и то же время как A, так и B совершают поворот на один и тот же угол за равное время. Это утверждение справедливо, так как рассматривается вращение единого твёрдого тела. То есть такого предмета, расстояние между любыми точками которого всегда остаётся одинаковым. При движении цилиндра происходит одновременно поступательное и вращательное перемещение, поэтому сложное движение представляют как комбинацию этих двух видов изменений положения. Характеризуется оно двумя величинами:
- периодом;
- частотой.

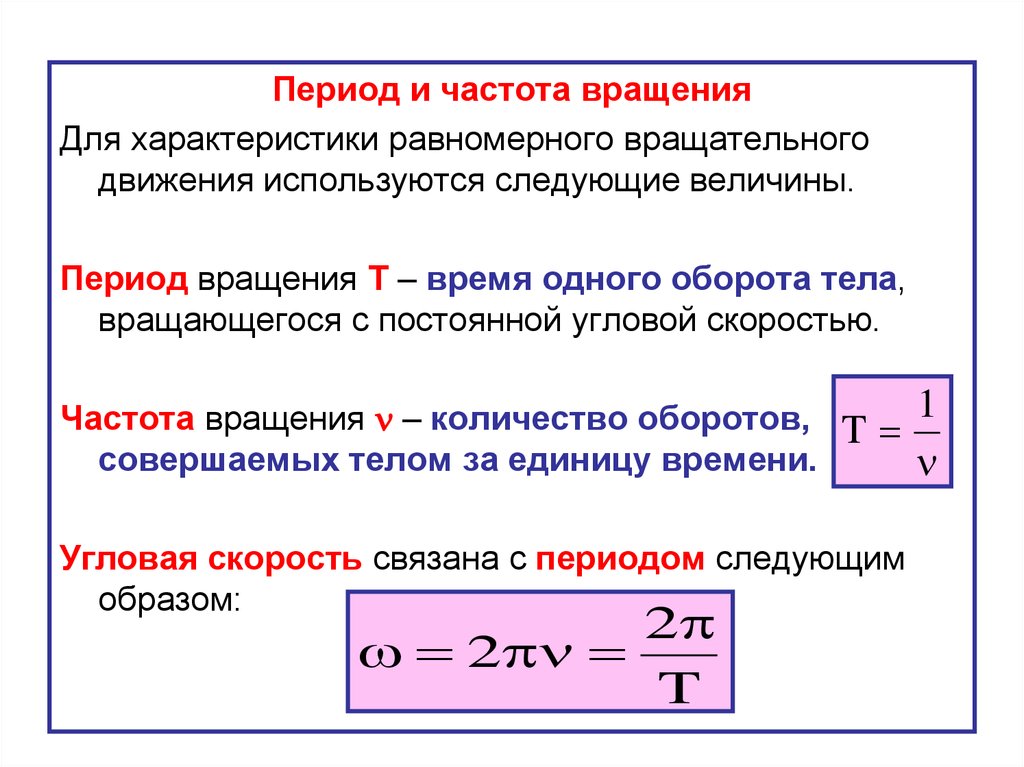
Поворот на один оборот занимает определённое время. У него есть своё название — период вращения. Обозначается он буквой T. Измеряется в любых единицах времени. В СИ в их качестве приняты секунды [с]. Например, период вращения минутной стрелки составляет один час. Число оборотов, совершённых телом, обозначают буквой N.
Допустим, за 10 секунд тело совершит пять оборотов. Чтобы найти период, нужно время, за которое произошло одно вращение, поделить на совершённое их число. Значит, формула, связывающая обороты со временем и периодом, будет выглядеть так: T = t / N.
Можно представить, что тело совершает 10 оборотов за пять секунд. Для того чтобы найти, сколько понадобится времени для совершения одного вращения, нужно число всех оборотов разделить на время. Полученное значение называют частотой вращения (n). По сути, это величина, равняющаяся числу оборотов, совершаемых телом за единицу времени: n = N / t. Измеряется она в СИ в оборотах / секунду. Так как в числителе стоит безразмерная величина, то частоту измеряют в [c-1]. Например, частота вращения Земли равняется одному обороту в сутки.
Так как в числителе стоит безразмерная величина, то частоту измеряют в [c-1]. Например, частота вращения Земли равняется одному обороту в сутки.
Между частотой и периодом существует связь. Если сравнить формулы, описывающие их, то можно заметить, что в них числитель и знаменатель поменялись местами. Значит, частота — это величина, обратная периоду: n = 1 / T. Соответственно, верным будет и равенство: T = 1 / n.
Линейная и угловая скорость
Любая точка, движущаяся вокруг оси, проходит определённый путь, который можно определить, зная её скорость и затраченное время. Пусть имеются две точки A и B, определяющиеся радиусами r1 и r2. При этом r2 больше r1. Скорость — это векторная величина. Она имеет направление. Поскольку за один оборот B проходит больше путь, то скорость её вращения будет превышать показатель для точки A, то есть V2 > V1. Параметр, определяющий скорость точек на вращающемся теле, называют линейным.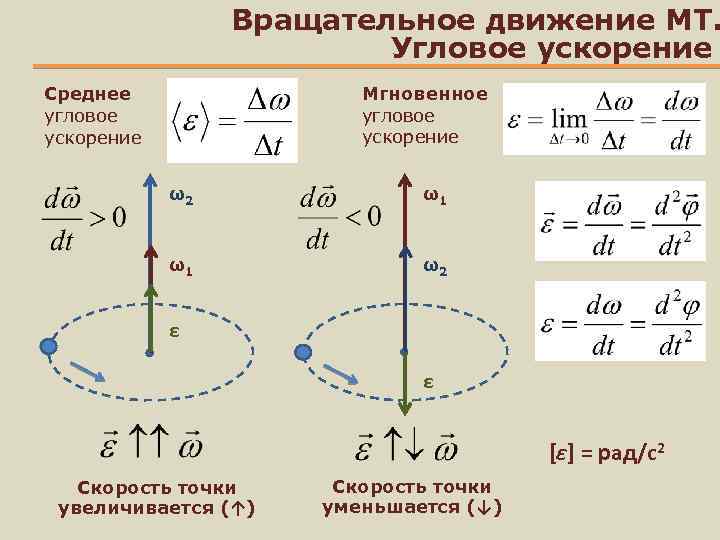 Именно такими и являются V1 и V2.
Именно такими и являются V1 и V2.
Очевидно, что при вращательном движении линейные скорости постоянно изменяют своё направление. Но если рассматривать модуль величин, то для одних случаев перемещения он будет постоянным, а для других нет. Самый простой случай, который позволяет исследовать вращение является поступательный. Чтобы дать такому перемещению определение, нужно понимать, что равномерным в физике называют движение, при котором тело проходит равные участки пути за любые одинаковые промежутки времени.
Следовательно, равномерное вращение твёрдого предмета — это движение по окружности, при котором за любые равные промежутки времени тело поворачивается на одну и ту же величину угла. Другими словами, совершается одинаковое количество оборотов в выбранном временном интервале. Допустим, тело за секунду совершит один оборот. Если взять промежуток в десять раз больше, то отношение величин не изменится. То есть период и частота при равномерном вращении остаются постоянными.
Константой будет оставаться и линейная скорость. Но её значение зависит от расстояния, на котором находится точка от оси вращения. Когда A совершит один оборот, то пройденный ею путь будет равен длине окружности L. Чтобы найти скорость, нужно L разделить на время, затраченное на выполнение действия. Фактически им является период. Отсюда следует, что формулу для линейной скорости можно записать так: V = L / T. Так как длина окружности равняется 2pr, то выражение примет вид: V = 2pr / T. Но вращательное движение можно охарактеризовать и частотой. Поскольку T = 1 /n, формулу можно переписать: V = n * 2pr.
Охарактеризовать количественно вращение можно угловой скоростью. Это физическая величина, равная отношению угла поворота тела ко времени, за которое он произошёл.
Обозначается она ω и равняется ω = φ / t. Измеряется в радианах, делённых на секунду. При этом угол поворота радиуса φ одинаковый для любой точки в поворачивающимся твёрдом теле.
youtube.com/embed/_YVo7BtcvRE» allowfullscreen=»allowfullscreen»>
Ускорение движения
Если движение равномерное, то скорость тела направлена по касательной и связана с угловой соотношением V = ω * r. При этом точка испытывает ускорение, направленное к центру окружности. Вычисляется она по формуле: a = V2 / r или a = ω 2 * r. При повороте тела на небольшой угол φ угловую скорость можно определить из соотношения ω = Δ φ / Δ t, где:
- Δφ — угол поворота тела;
- Δt — время, за которое точка совершила поворот.
Если вращение абсолютно-равномерное, то Δt может быть любым. В ином случае ω является мгновенной угловой скоростью. При неравномерном движении V ≠ const, тогда ω тоже не будет постоянной величиной. Изменение Δω определяется разностью между принятым положением и начальным: Δω = ω — ω0.
Учитывая, что ускорение a = (V — V0) / Δt, по аналогии можно записать выражение: ω — ω0 / Δt. Это отношение называется угловым ускорением. Обозначают греческой буквой E. Находят же по формуле: E = Δ ω / Δ t. Измеряется ускорение в радианах, делённых на секунду в квадрате [рад/ с2]. Таким образом, угловым ускорением тела при вращательном движении называют физическую величину, равную отношению изменения угловой скорости за небольшой интервал времени к длительности этого промежутка.
Обозначают греческой буквой E. Находят же по формуле: E = Δ ω / Δ t. Измеряется ускорение в радианах, делённых на секунду в квадрате [рад/ с2]. Таким образом, угловым ускорением тела при вращательном движении называют физическую величину, равную отношению изменения угловой скорости за небольшой интервал времени к длительности этого промежутка.
Поскольку ускорение представляет собой изменение скорости ко времени, то можно записать: ΔV / Δt = ΔVr / Δt + Δ Ve / Δt, где: ΔVr — радиальное значение, ΔVe — угловое. Получается, что в выражении справа стоит ускорение a, а слева две составляющие, обусловленные криволинейностью и неравномерностью движения. Таким образом, полное ускорение представляет собой сумму двух взаимно перпендикулярных ускорений: a = ar + ae.
Следует отметить, что приведённые формулы справедливы не только для вращательного перемещения, но также и для возвратно-поступательного.
Если тело ускоряется, то угол между векторами ar и ae будет острым, при замедлении же он станет тупым. При этом вращение с постоянным угловым ускорение описывается выражением: ω(t) = ω0 + E * t.
При этом вращение с постоянным угловым ускорение описывается выражением: ω(t) = ω0 + E * t.
Кинематика. Основные кинематические характеристики прямолинейного и криволинейного движения
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Лекция 1
1. Механика
1.1. Кинематика
Основные кинематические характеристики
прямолинейного и криволинейного движения: путь,
перемещение, скорость и ускорение. Нормальное,
Нормальное,
тангенциальное и полное ускорения. Кинематика
вращательного движения: угловой путь, угловая
скорость и угловое ускорение, их связь с линейными
величинами. Период и частота вращения.
Механика
Механическое движение
Механическим движением тела называется изменение его
положения в пространстве относительно других тел с течением
времени.
Система отсчета
Тело, которое считается неподвижным, и по отношению к которому
определяется положение других тел, называют телом отсчета. Тело
отсчета вместе со связанной с ним системой координат образуют
систему отсчета.
Относительность механического движения
Зависимость характера движения от выбора тела, относительно
которого это движение определяется, называется
относительностью движения. Всякое движение, и покой в
частности, является относительным.
Кинематика
Абсолютно твердое тело
Абсолютно твердым называется тело, деформацией которого
можно пренебречь. В таком теле расстояние между двумя точками
В таком теле расстояние между двумя точками
неизменно во времени.
Поступательное движение тела
Движение тела, при котором все его точки движутся одинаково,
называется поступательным. При таком движении любая прямая,
жестко связанная с телом, перемещается в пространстве,
оставаясь параллельной самой себе.
Материальная точка
Тело, размерами которого в данных условиях можно пренебречь
(по сравнению с масштабом движения), называется материальной
точкой.
Траектория движения
Траекторией движения материальной точки называется линия,
которую эта точка описывает в пространстве при своем движении.
Путь
Путь — скалярная физическая величина, численно равная длине
отрезка траектории, пройденного телом за время движения.
S S (t )
S S (t2 ) S (t1 )
t t2 t1
Перемещение
Перемещением тела (материальной точки) называется
направленный отрезок прямой (вектор), соединяющий начальное и
конечное положение тела.
r r r
2
z
r1
Прямолинейное движение
S
A
r
B
r2
y
x
1
Движение называется прямолинейным,
если его траектория представляет
собой прямую линию.
При прямолинейном движении путь и
перемещение совпадают: r S
При криволинейном движении они
совпадают в пределе для бесконечно
малого перемещения:
dr dS
Линейная скорость
Линейной скоростью перемещения тела называют векторную
физическую величину, характеризующую процесс изменения
пространственного положения тела относительно выбранной
системы отсчета, численно равную перемещению тела в единицу
времени и совпадающую по направлению с этим перемещением.
Единица скорости
За единицу скорости (м/сек) принимают скорость такого движения,
при котором тело за 1 сек перемещается на расстояние 1 м.
r
v
t
vA
z
A
r
B
vB
y
x
Мгновенная скорость:
r
d
r
v lim
t 0 t
dt
d
r
dS
v v
dt
dt
Мгновенная скорость
Мгновенная скорость, или скорость в данной точке, равна
отношению достаточно малого перемещения на участке
траектории, включающем эту точку, к малому промежутку времени,
в течение которого это перемещение совершается.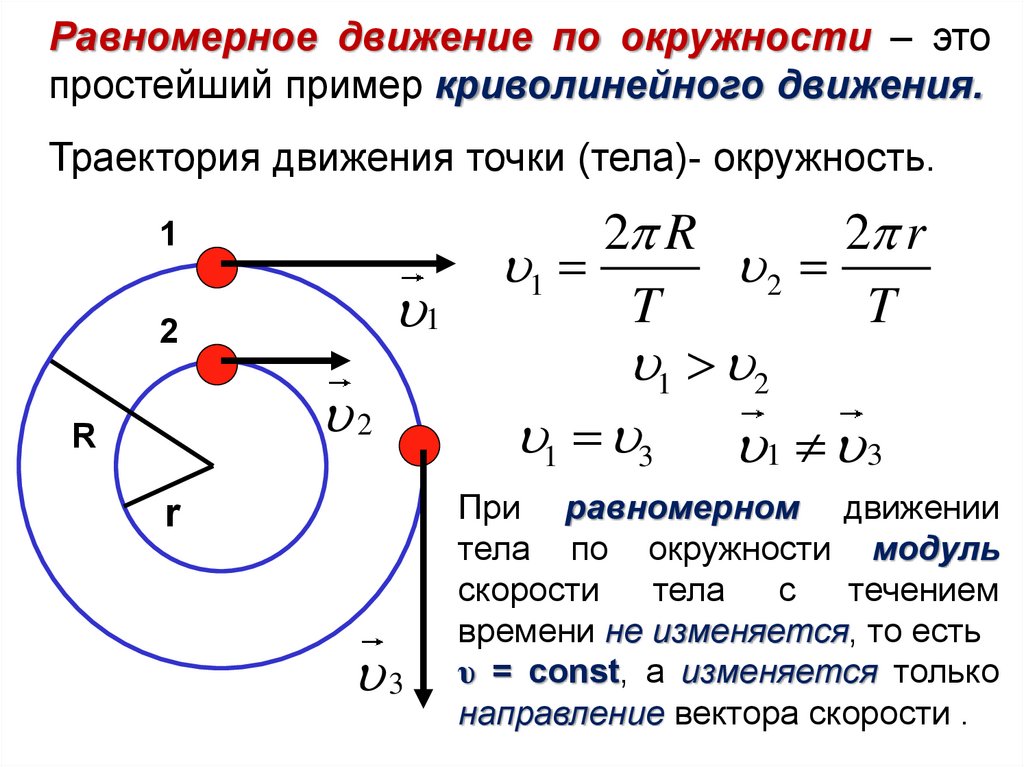 Направлена по
Направлена по
касательной к траектории в данной точке.
Равномерное прямолинейное движение
Равномерным прямолинейным называется такое прямолинейное
движение, при котором тело (материальная точка) за любые
равные промежутки времени проходит одинаковый путь.
Средняя скорость
Средней скоростью движения на данном участке пути называется
отношение длины этого участка пути к промежутку времени, за
которой этот участок пройден.
Средняя скорость есть скорость такого равномерного движения,
при котором тело прошло бы данный участок пути за тот же
промежуток времени.
S ( S S )
v ср v v
t
2
1
(t 2 t1 )
Принцип независимости движений
Если тело участвует одновременно в нескольких движениях, то
каждое из них совершается независимо от остальных.
n
r r1 r2 rn rn
i 1
Сложение скоростей
Скорость тела относительно неподвижной системы координат
равна геометрической (векторной) сумме скорости тела
относительно подвижной системы координат и скорости подвижной
системы координат относительно неподвижной.
n
drn
dr dr1 dr2
v
v1 v 2 v n v n
dt dt dt
dt
i 1
При движении вдоль одной прямой скорости направленные по
направлению движения берутся со знаком «+», против движения со
знаком «–».
Линейное ускорение
Линейное ускорение — векторная физическая величина,
характеризующая процесс изменения линейной скорости с
течением времени, численно равная изменению скорости в единицу
времени и совпадающая по направлению с направлением этого
изменения.
v
Единица ускорения
a
t
За единицу ускорения (м/сек2) в системе СИ принимают ускорение
такого движения, при котором тело за 1 сек изменяет свою скорость
на 1 м/сек.
Мгновенное ускорение
Мгновенное ускорение, или ускорение в данной точке, равно
отношению достаточно малого изменения скорости на участке
траектории, включающем эту точку, к малому промежутку времени,
в течении которого это изменение совершается.
v d v
a lim
t 0 t
dt
d 2 r
d 2S
dv
a a
2 2
dt
dt
dt
A
Тангенциальное ускорение
vА
v
B
Тангенциальным (касательным) ускорением называется
составляющая ускорения, обусловленная изменением
модуля вектора скорости.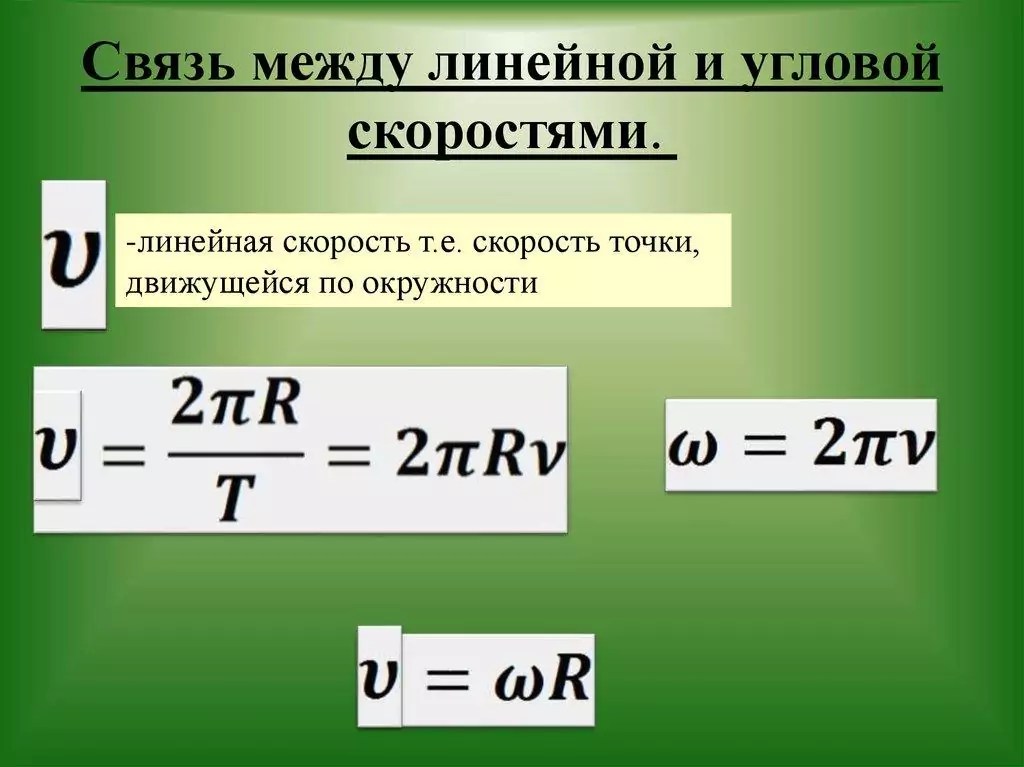
dv
vB
a
Нормальное ускорение
vA
A
Нормальным (центростремительным) ускорением
называется составляющая ускорения, обусловленная
изменение направления вектора скорости.
a
an
a
vA
r
О
dt
B
v
vB
v AB
v
АO
v r v t
v
R
R
v v 2
t
R
v2
an
R
v v 2
an lim
t 0 t
R
dv v
2
2
a a a an
dt R
2
2
2
Частные случаи криволинейного движения
1.
a 0
an 0
Равномерное прямолинейное движение
2.
a const
an 0
Равнопеременное прямолинейное движение
3.
a 0
an const
Равномерное движение по окружности
4. a const
an const
Равнопеременное движение по окружности
Кинематические уравнения и графики
Равномерное движение
v const
S v t
a 0
При равномерном движении график зависимости пути от времени
есть прямая линия, проходящая через начало системы координат.
При равномерном движении график зависимости скорости от
времени есть прямая линия, проходящая параллельно оси
времени.
При равномерном движении ускорение тела равно нулю.
v
v
S
t
t
t1
t2
t
Равнопеременное движение
a t2
S v0 t
2
v v0 a t
a const
При равнопеременном движении график зависимости скорости от
времени есть прямая линия.
При равнопеременном движении график зависимости ускорения от
времени есть прямая, параллельная оси времени.
a
v
S
a 0
a 0
a 0
a 0
t
t
t
Вращательное движение
Вращательным движением твердого тела вокруг неподвижной оси
называется такое движение, при котором все точки тела двигаются
по окружности, центры которых лежат на одной прямой,
называемой осью вращения. Ось вращения перпендикулярна
плоскости, в которой лежат эти окружности.
Вращение тела
Радиусы-векторы, соединяющие все точки твердого тела с
центрами описываемых ими окружностей, поворачиваются за один
и тот же промежуток времени на одинаковый угол, т. е. описывают
е. описывают
одинаковый угловой путь.
Угловой путь
Угловой путь тела — векторная физическая величина,
характеризующая вращение тела вокруг неподвижной оси,
численно равная углу поворота за определенный промежуток
времени и направленная вдоль оси вращения так, что из конца
вектора вращение видно происходящим против часовой стрелки.
Единица угла поворота
За единицу угла поворота в системе СИ принимают
1 радиан (рад) — такой угол, длина дуги которого
равна радиусу. В полном обороте 2 радиан.
Угловая скорость
Угловой скоростью вращения тела называют векторную
физическую величину, характеризующую быстроту вращения тела
вокруг неподвижной оси, численно равную угловому пути в единицу
времени и направленную вдоль оси вращения. Направление
угловой скорости вдоль оси вращения определяется по правилу
«буравчика», т.е. таким образом, чтобы получился правый винт.
d
dt
Единица угловой скорости
За единицу угловой скорости рад/сек в системе СИ принимают
угловую скорость такого вращения, при котором тело за 1 сек
поворачивается на угол равный 1 рад.
Угловое ускорение
Угловым ускорением вращения тела называют векторную
физическую величину, характеризующую быстроту изменения
угловой скорости и численно равную изменению угловой скорости в
единицу времени. Вектор углового ускорения направлен по оси
вращения либо в сторону угловой скорости (при ускоренном
вращении), либо противоположно ей (при замедленном вращении).
d d 2
2
dt
dt
Единица углового ускорения
За единицу углового ускорения рад/сек2 в системе СИ принимают
угловое ускорение такого вращения, при котором угловая скорость
вращения тела за 1 сек изменяется 1 рад/сек.
Равномерное вращение
Равномерным вращением твердого тела называется такое
вращение, при котором тело за любые равные промежутки
поворачивается на одинаковый угол поворота.
Период обращения
Периодом обращения называют скалярную физическую величину,
численно равную промежутку времени, в течение которого тело
совершает полный оборот,
2
2
T
т. е. поворачивается на угол 2 .
е. поворачивается на угол 2 .
t
Частота обращения
T
Частотой обращения называют скалярную физическую величину,
численно равную числу оборотов, совершаемых за единицу
времени.
N 1
t
T
2
2
Связь между линейными и угловыми единицами
Вращательное движение
Поступательное движение
Путь S
S R
Угол поворота
v R
Угловая скорость
Угловое ускорение
Тангенциальное ускорение a R
2
v
Нормальное ускорение
an
2 R
R
Линейная скорость v
Кинематические уравнения и графики
Равномерное вращение
t
const
0
При равномерном вращении график зависимости угла поворота от
времени есть прямая линия, проходящая через начало системы
координат.
При равномерном вращении график зависимости угловой скорости
от времени есть прямая линия, проходящая параллельно оси
времени.
При равномерном вращении угловое ускорение тела равно нулю.
t
t
t1
t2
t
Равнопеременное вращение
0 t
t2
0 t
2
const
При равнопеременном вращении график зависимости угловой
скорости от времени есть прямая линия.
При равнопеременном вращении график зависимости углового
ускорения от времени есть прямая, параллельная оси времени.
0
0
0
0
t
t
t
English
Русский
Правила
6.3: Равномерное круговое движение — Physics LibreTexts
-
- Последнее обновление
- Сохранить как PDF
-
- Идентификатор страницы
- 19400
- Howard Martin пересмотрено Аланом Нг
- University of Wisconsin-Madison
- Вектор скорости \(\vec v\) всегда касается окружности.
- Вектор ускорения \(\vec a\) всегда перпендикулярен вектору скорости, потому что величина вектора скорости не меняется.
92/р\). - Угловая скорость \(\omega\) связана с величиной вектора скорости соотношением \(v=\omega R\) и является постоянной.
- Угловое ускорение \(\alpha\) равно нулю при равномерном круговом движении, так как угловая скорость не меняется.
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec N\), нормальная сила, действующая на поверхность.
- \(\vec T\), сила натяжения струны.
- А
- Б
- С
- Д
- Ответить
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec N\), нормальная сила, приложенная дорогой вверх.
- \(\vec f_s\), сила трения покоя между шинами и дорогой. Это статическое трение, потому что поверхность шины не двигается относительно поверхности дороги, если автомобиль не буксует. Сила трения покоя имеет величину не более \(f_s\leq\mu_sN\).
 2 &\ leq \ mu_s g R \\ \ поэтому v &\ leq \ sqrt {\ mu_s g R} \ end {align} \ ] Таким образом, если скорость меньше \(\sqrt{\mu_s g R}\), автомобиль не будет скользить и величина силы трения покоя, приводящая к ускорению по направлению к центру окружности, будет быть меньше или равно его максимально возможному значению.
2 &\ leq \ mu_s g R \\ \ поэтому v &\ leq \ sqrt {\ mu_s g R} \ end {align} \ ] Таким образом, если скорость меньше \(\sqrt{\mu_s g R}\), автомобиль не будет скользить и величина силы трения покоя, приводящая к ускорению по направлению к центру окружности, будет быть меньше или равно его максимально возможному значению.
Обсуждение:
Модель максимальной скорости, с которой автомобиль может двигаться по кривой, имеет смысл, потому что:
- Размерность \(\sqrt{\mu_s g R}\) — это скорость.
- Скорость тем больше, чем больше радиус кривой (можно двигаться быстрее по более широкой кривой без заноса).
- Скорость больше, если коэффициент трения велик (чем больше сила трения, тем больше может поддерживаться радиальное ускорение).
Пример \(\PageIndex{2}\)
Рисунок \(\PageIndex{6}\): Шарик, прикрепленный к веревке, совершает круговое движение в вертикальной плоскости.
Мяч прикреплен к невесомой нити и совершает круговое движение по окружности радиуса \(R\), лежащей в вертикальной плоскости, как показано на рисунке \(\PageIndex{6}\).
 Может ли скорость мяча быть постоянной? Какова минимальная скорость мяча в верхней части круга, если он в состоянии сделать это вокруг круга?
Может ли скорость мяча быть постоянной? Какова минимальная скорость мяча в верхней части круга, если он в состоянии сделать это вокруг круга?Решение :
Силы, действующие на шар:
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec T\), сила натяжения струны.
На рисунке \(\PageIndex{7}\) показана диаграмма свободного тела для сил, действующих на мяч в трех разных точках вдоль траектории окружности.
Рисунок \(\PageIndex{7}\): Шарик, прикрепленный к веревке, совершает круговое движение в вертикальной плоскости.
Для того, чтобы мяч двигался по кругу, на мяче должна быть по крайней мере составляющая чистой силы, которая всегда направлена к центру круга. В нижней половине окружности (позиции 1 и 2) только натяжение может иметь составляющую, направленную к центру окружности.
Рассмотрим, в частности, положение, обозначенное цифрой 2, когда струна горизонтальна и натяжение равно \(\vec T_2\).
 Диаграмма свободного тела на рисунке \(\PageIndex{7}\) также показывает векторную сумму веса и напряжения в положении 2 (красная стрелка, обозначенная \(\sum \vec F\)), которая указывает вниз и к слева. Таким образом, очевидно, что вектор ускорения не может быть направлен к центру окружности, и ускорение будет иметь компоненты, которые являются как тангенциальными (\(a_T\)) к окружности, так и радиальными (\(a_R\)), как показано вектором \(\vec a_2\) на рисунке \(\PageIndex{7}\).
Диаграмма свободного тела на рисунке \(\PageIndex{7}\) также показывает векторную сумму веса и напряжения в положении 2 (красная стрелка, обозначенная \(\sum \vec F\)), которая указывает вниз и к слева. Таким образом, очевидно, что вектор ускорения не может быть направлен к центру окружности, и ускорение будет иметь компоненты, которые являются как тангенциальными (\(a_T\)) к окружности, так и радиальными (\(a_R\)), как показано вектором \(\vec a_2\) на рисунке \(\PageIndex{7}\).Радиальная составляющая ускорения изменит направление вектора скорости так, что мяч останется на окружности, а тангенциальная составляющая уменьшит величину вектора скорости. Таким образом, согласно нашей модели, мяч не может двигаться по окружности с постоянной скоростью, а скорость должна уменьшаться по мере перехода от положения 2 к положению 3, как бы ни тянули за нитку (вы можете убедиться в этом сами). это путем рисования диаграммы свободного тела в любой точке между точками 2 и 3).
Минимальная скорость мяча в верхней части круга определяется условием, что натяжение нити равно нулю только в верхней части траектории (позиция 3).
 2}{R}\\ \поэтому v_{min}&=\sqrt{\frac{gR}{m}}\end{aligned}\] — это минимальная скорость в верхней части траектории, при которой мяч может двигаться по кругу. Натяжение нити будет меняться по мере того, как мяч будет двигаться по кругу, и будет самым высоким в нижней части траектории, поскольку натяжение должно быть больше силы тяжести, чтобы результирующая сила в нижней части траектории была направлена вверх (к центр круга).
2}{R}\\ \поэтому v_{min}&=\sqrt{\frac{gR}{m}}\end{aligned}\] — это минимальная скорость в верхней части траектории, при которой мяч может двигаться по кругу. Натяжение нити будет меняться по мере того, как мяч будет двигаться по кругу, и будет самым высоким в нижней части траектории, поскольку натяжение должно быть больше силы тяжести, чтобы результирующая сила в нижней части траектории была направлена вверх (к центр круга).Обсуждение:
Модель минимальной скорости мяча в верхней части круга имеет смысл, потому что:
- \(\sqrt{\frac{gR}{m}}\) имеет размерность скорость.
- Минимальная скорость больше, если окружность имеет больший радиус (попробуйте это с грузом, прикрепленным к концу нити).
- Минимальная скорость тем больше, чем больше масса (опять же, попробуйте дома!).
Упражнение \(\PageIndex{2}\)
Рассмотрим мяч, прикрепленный к веревке, который вращается по вертикальному кругу (например, изображенному на рисунке \(\PageIndex{6}\)).
 Если вы укоротите нить, как изменится минимальная угловая скорость (измеренная в верхней части траектории), необходимая для того, чтобы мяч совершил движение по кругу?
Если вы укоротите нить, как изменится минимальная угловая скорость (измеренная в верхней части траектории), необходимая для того, чтобы мяч совершил движение по кругу?- Уменьшится
- Он останется прежним
- Увеличится
- Ответить
Кривые с наклоном
Как мы видели в примере 6.3.1 , существует максимальная скорость, с которой автомобиль может пройти поворот, прежде чем он начнет скользить. Вы, наверное, заметили, что дороги, особенно автомагистрали, имеют крен там, где есть повороты. Гоночные трассы для автомобилей, которые движутся по овалу (скучный вид автомобильных гонок), также имеют виражи. Как мы увидим, это позволяет увеличить скорость транспортных средств при движении по кривой; или, скорее, делает повороты безопаснее, чем скорость, с которой транспортные средства бы салазки повыше. В Примере 6.3.1 мы видели, что именно сила статического трения между шинами автомобиля и дорогой обеспечивала единственную силу с составляющей, направленной к центру круга.
 Идея использования кривой с наклоном состоит в том, чтобы изменить направление нормальной силы между дорогой и автомобильными шинами так, чтобы она тоже имела составляющую, направленную к центру круга.
Идея использования кривой с наклоном состоит в том, чтобы изменить направление нормальной силы между дорогой и автомобильными шинами так, чтобы она тоже имела составляющую, направленную к центру круга.Рассмотрим автомобиль, изображенный на рисунке \(\PageIndex{8}\), который, если смотреть сзади, совершает левый поворот по кривой, наклоненной под углом \(\theta\) по отношению к горизонтали и поддающейся моделированию как дуга из окружности радиуса \(R\).
Рисунок \(\PageIndex{8}\): Автомобиль, въезжающий на страницу и объезжающий вираж, поворачивает влево (центр круга находится слева).
Силы, воздействующие на автомобиль, такие же, как и в Пример 6.3.1 , за исключением того, что они направлены в разные стороны. Силы равны:
- \(\vec F_g\), его вес с величиной \(мг\).
- \(\vec N\), нормальная сила, действующая на дорогу перпендикулярно поверхности дороги.
- \(\vec f_s\), сила трения покоя между шинами и дорогой.
 Это статическое трение, потому что поверхность шины не двигается относительно поверхности дороги, если автомобиль не буксует. Сила трения покоя имеет величину не более \(f_s\leq\mu_sN\) и перпендикулярна нормальной силе. Сила может быть направлена либо вверх, либо вниз, , в зависимости от других сил, действующих на автомобиль .
Это статическое трение, потому что поверхность шины не двигается относительно поверхности дороги, если автомобиль не буксует. Сила трения покоя имеет величину не более \(f_s\leq\mu_sN\) и перпендикулярна нормальной силе. Сила может быть направлена либо вверх, либо вниз, , в зависимости от других сил, действующих на автомобиль .
Диаграмма свободного тела для сил, действующих на автомобиль, показана на рис. 6.3.9., а также ускорение (которое находится в радиальном направлении, к центру круга) и наш выбор системы координат (выбор \(x\) параллельно ускорению). Направление силы трения покоя неизвестно априори и зависит от скорости автомобиля:
- Если скорость автомобиля равна нулю, сила трения покоя направлена вверх. При нулевой скорости радиальное ускорение равно нулю, и поэтому сумма сил должна быть равна нулю. Препятствующим движению автомобиля будет скольжение по кривой с наклоном (точно так же, как блок на наклонной поверхности).

- Если скорость автомобиля очень велика, сила трения покоя направлена вниз, так как препятствующее движению автомобиля движение будет скользить вверх по берегу. Естественным движением автомобиля является прямолинейное движение (первый закон Ньютона). Если компоненты нормальной силы и силы трения покоя, направленные к центру круга, слишком малы, чтобы позволить машине повернуться, то машина будет скользить вверх по берегу (поэтому препятствующее движение будет движением вверх по берегу, а сила трения покоя направлена вниз).
Рисунок \(\PageIndex{9}\): Диаграмма свободного тела для сил, действующих на автомобиль. Направление силы трения покоя определить невозможно, так как оно зависит от ускорения автомобиля, поэтому оно показано дважды (пунктирными линиями).
Таким образом, существует «идеальная скорость» при в котором сила трения покоя точно равна нулю, а составляющая \(х\) нормальной силы отвечает за радиальное ускорение. На более высоких скоростях сила трения покоя направлена вниз и увеличивается по величине, чтобы удерживать ускорение автомобиля по направлению к центру круга.
 При некоторой максимальной скорости сила трения достигнет своего максимального значения и больше не сможет удерживать ускорение автомобиля, направленное к центру круга. На скоростях ниже идеальной сила трения направлена вверх, чтобы предотвратить скольжение автомобиля по берегу. Если коэффициент статического трения слишком низкий, возможно, что на низких скоростях автомобиль начнет скользить по берегу (поэтому будет минимальная скорость, ниже которой автомобиль начнет скользить вниз). 92}{gR}\\ \therefore v_{ideal} &=\sqrt{gR\tan\theta}\end{aligned}\] При этой скорости сила трения покоя равна нулю. На практике можно использовать это уравнение, чтобы определить, какой угол крена использовать при проектировании дороги, чтобы идеальная скорость была около ограничения скорости или средней скорости движения. Мы оставляем в качестве упражнения определение максимальной скорости, с которой автомобиль может двигаться по кривой, прежде чем выскользнуть из нее.
При некоторой максимальной скорости сила трения достигнет своего максимального значения и больше не сможет удерживать ускорение автомобиля, направленное к центру круга. На скоростях ниже идеальной сила трения направлена вверх, чтобы предотвратить скольжение автомобиля по берегу. Если коэффициент статического трения слишком низкий, возможно, что на низких скоростях автомобиль начнет скользить по берегу (поэтому будет минимальная скорость, ниже которой автомобиль начнет скользить вниз). 92}{gR}\\ \therefore v_{ideal} &=\sqrt{gR\tan\theta}\end{aligned}\] При этой скорости сила трения покоя равна нулю. На практике можно использовать это уравнение, чтобы определить, какой угол крена использовать при проектировании дороги, чтобы идеальная скорость была около ограничения скорости или средней скорости движения. Мы оставляем в качестве упражнения определение максимальной скорости, с которой автомобиль может двигаться по кривой, прежде чем выскользнуть из нее.Силы инерции при круговом движении
Когда вы сидите в автомобиле, который движется по кривой, вы почувствуете, что вас толкает наружу, в сторону от центра круга, по которому движется автомобиль.
 Это происходит из-за вашей инерции (Первый закон Ньютона), и ваше тело двигалось бы по прямой линии, если бы машина не оказывала на вас суммарной силы по направлению к центру круга. Вы не столько ощущаете силу, толкающую вас наружу, сколько эффект от автомобильного кресла, толкающего вас внутрь; если бы вы прислонились к стороне автомобиля, которая находится снаружи кривой, вы бы почувствовали, как сторона автомобиля толкает вас внутрь к центру кривой, даже если «чувствуется», что вы толкаете наружу против поворота. сторона автомобиля.
Это происходит из-за вашей инерции (Первый закон Ньютона), и ваше тело двигалось бы по прямой линии, если бы машина не оказывала на вас суммарной силы по направлению к центру круга. Вы не столько ощущаете силу, толкающую вас наружу, сколько эффект от автомобильного кресла, толкающего вас внутрь; если бы вы прислонились к стороне автомобиля, которая находится снаружи кривой, вы бы почувствовали, как сторона автомобиля толкает вас внутрь к центру кривой, даже если «чувствуется», что вы толкаете наружу против поворота. сторона автомобиля.Если мы смоделируем ваше движение, глядя на вас с земли, мы включим силу трения между автомобильным сиденьем (или боковой частью автомобиля, или обоими) и вами, которая указывает на центр круга, так что сумма сил, действующих на вас, направлена к центру круга. Мы также можем смоделировать ваше движение по неинерциальной раме автомобиля. Как вы помните, поскольку это неинерциальная система отсчета, нам нужно включить дополнительную инерционную силу, \(\vec F_I\), которая указывает направление, противоположное ускорению автомобиля, с величиной \(F_I=ma_R\ ) (если чистое ускорение автомобиля равно \(a_R\)).
 2}{R} &= 0\end{ выровнены}\] что, конечно, математически точно эквивалентно. Сила инерции не является реальной силой в том смысле, что на нее ничто не действует. Это вступает в игру только потому, что мы пытаемся использовать законы Ньютона в неинерциальной системе отсчета. Тем не менее, он обеспечивает хорошую модель для описания ощущения, которое мы испытываем, когда автомобиль выталкивает наружу, когда машина проходит поворот. Иногда люди называют эту силу «центробежной» силой, что означает «сила, направленная от центра». Однако вы должны помнить, что это не реальная сила, действующая на объект, а результат моделирования движения в неинерциальной системе отсчета.
2}{R} &= 0\end{ выровнены}\] что, конечно, математически точно эквивалентно. Сила инерции не является реальной силой в том смысле, что на нее ничто не действует. Это вступает в игру только потому, что мы пытаемся использовать законы Ньютона в неинерциальной системе отсчета. Тем не менее, он обеспечивает хорошую модель для описания ощущения, которое мы испытываем, когда автомобиль выталкивает наружу, когда машина проходит поворот. Иногда люди называют эту силу «центробежной» силой, что означает «сила, направленная от центра». Однако вы должны помнить, что это не реальная сила, действующая на объект, а результат моделирования движения в неинерциальной системе отсчета.Упражнение \(\PageIndex{3}\)
Джейми едет на своем трехколесном велосипеде вокруг круглого пруда. Джейми чувствует центробежную силу с величиной \(F_I\). Если Джейми будет крутить педали в два раза быстрее, какой будет величина центробежной силы, которую он будет испытывать?
- \(\sqrt{2}F_I\)
- \(\frac{1}{2}F_I\)
- \(2F_I\)
- \(4F_I\)
- Ответить
Сноски
1.
 Сумма сил часто называется «чистой силой», действующей на объект, а в конкретном случае равномерного кругового движения эту результирующую силу иногда называют «центростремительной силой», однако это не сила. сама по себе, и это всегда сумма сил, направленных к центру круга.
Сумма сил часто называется «чистой силой», действующей на объект, а в конкретном случае равномерного кругового движения эту результирующую силу иногда называют «центростремительной силой», однако это не сила. сама по себе, и это всегда сумма сил, направленных к центру круга.
Эта страница под названием 6.3: Равномерное круговое движение распространяется под лицензией CC BY-SA, автором, ремиксом и/или куратором выступил Ховард Мартин, редактируемый Аланом Нг.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- Райан Мартин и др.
- Лицензия
- CC BY-SA
- Показать оглавление
- нет
-
- Теги
-

Момент инерции
Момент инерции
Больше сравнений линейного и углового движения Индекс Понятия момента инерции
Гиперфизика***** Механика ***** Вращение R Ступица Назад Сохранение линейного количества движения диктует, что, когда масса сталкивается с равной массой в состоянии покоя и прилипает к ней, комбинация должна двигаться с половиной скорости, потому что произведение массы и скорости должно оставаться постоянным.
С помощью веревки через трубку груз перемещается по горизонтальной окружности с угловой скоростью ω.
 Если нить натянута вниз так, что радиус равен половине первоначального радиуса, то закон сохранения углового момента диктует, что мяч должен иметь четырехкратную угловую скорость. Это связано с тем, что произведение момента инерции и угловой скорости должно оставаться постоянным, а уменьшение радиуса вдвое уменьшает момент инерции в четыре раза.
Если нить натянута вниз так, что радиус равен половине первоначального радиуса, то закон сохранения углового момента диктует, что мяч должен иметь четырехкратную угловую скорость. Это связано с тем, что произведение момента инерции и угловой скорости должно оставаться постоянным, а уменьшение радиуса вдвое уменьшает момент инерции в четыре раза.При соответствующем балансе сил круговая орбита может быть создана силой, действующей к центру. Действуя перпендикулярно скорости, он создает необходимую центростремительную силу, чтобы удерживать его по окружности.
Если вращающееся колесо и ось поддерживаются одним концом оси, то крутящий момент, создаваемый весом колеса и оси, создает крутящий момент, перпендикулярный угловому моменту колеса. Это изменяет его направление, но не его величину, в результате чего кончик оси очерчивает круг. Это называется прецессией и аналогично орбите массы под действием центральной силы.

Индекс Понятия момента инерции
Гиперфизика***** Механика ***** Вращение R Ступица Назад Момент инерции — это название, данное вращательной инерции, вращательному аналогу массы для линейного движения. Он появляется в соотношениях для динамики вращательного движения. Момент инерции должен быть указан относительно выбранной оси вращения. Для точечной массы момент инерции равен произведению массы на квадрат расстояния по перпендикуляру к оси вращения, I = mr 2 . Это отношение точечных масс становится основой для всех других моментов инерции, поскольку любой объект может быть построен из набора точечных масс.
Общие формы Примеры Общая форма Развертка для точечной массы Индекс Понятия момента инерции
Гиперфизика***** Механика ***** Вращение R Ступица Назад Индекс Понятия момента инерции
Гиперфизика***** Механика ***** Вращение R Ступица Назад Момент инерции определяется относительно определенной оси вращения.
 Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл.
Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл.Моменты инерции для обычных форм
Где момент инерции появляется в физических величинах Индекс Понятия момента инерции
Гиперфизика***** Механика ***** Вращение R Ступица Вернуться Поскольку момент инерции обычного объекта включает в себя непрерывное распределение массы на постоянно меняющемся расстоянии от любой оси вращения, расчет моментов инерции обычно включает исчисление, дисциплину математики, которая может обрабатывать такие непрерывные переменные.
 Поскольку момент инерции точечной массы определяется как
Поскольку момент инерции точечной массы определяется как, то момент инерции, вносимый бесконечно малым элементом массы dm, имеет такой же вид. Такой элемент массы называется дифференциальным элементом массы, а его момент инерции равен
Обратите внимание, что дифференциальный элемент момента инерции dI всегда должен определяться относительно конкретной оси вращения. Сумма по всем этим элементам массы называется интегралом по массе.
Обычно элемент массы dm выражается через геометрию объекта, чтобы интегрирование можно было проводить по объекту в целом (например, по длинному однородному стержню).
Назвав это общей формой, вероятно, уместно указать, что это общая форма только для осей, которые могут быть названы «главными осями», термин, который включает все оси симметрии объектов. Понятие момента инерции для общих объектов относительно произвольных осей — гораздо более сложный предмет. Момент инерции в таких случаях принимает форму математической тензорной величины, для полного определения которой требуется девять компонентов.

Как мы видели в главе 4, «равномерное круговое движение» определяется как движение по окружности с постоянной скоростью. Сейчас самое время вернуться к разделу 4.4, посвященному кинематике движения по окружности. В частности, для равномерного кругового движения объекта по окружности радиуса \(R\) следует вспомнить, что:
В частности, для равномерного кругового движения объекта по окружности радиуса \(R\) следует вспомнить, что:
В частности, следует помнить, что даже если скорость постоянна, вектор ускорения всегда отличен от нуля при равномерном круговом движении, потому что скорость меняет направление 92/р\). Поскольку ускорение направлено к центру окружности, мы иногда называем его «радиальным» ускорением (параллельным радиусу), \(a_R\), или «центростремительным» ускорением (направленным к центру), \(a_c \).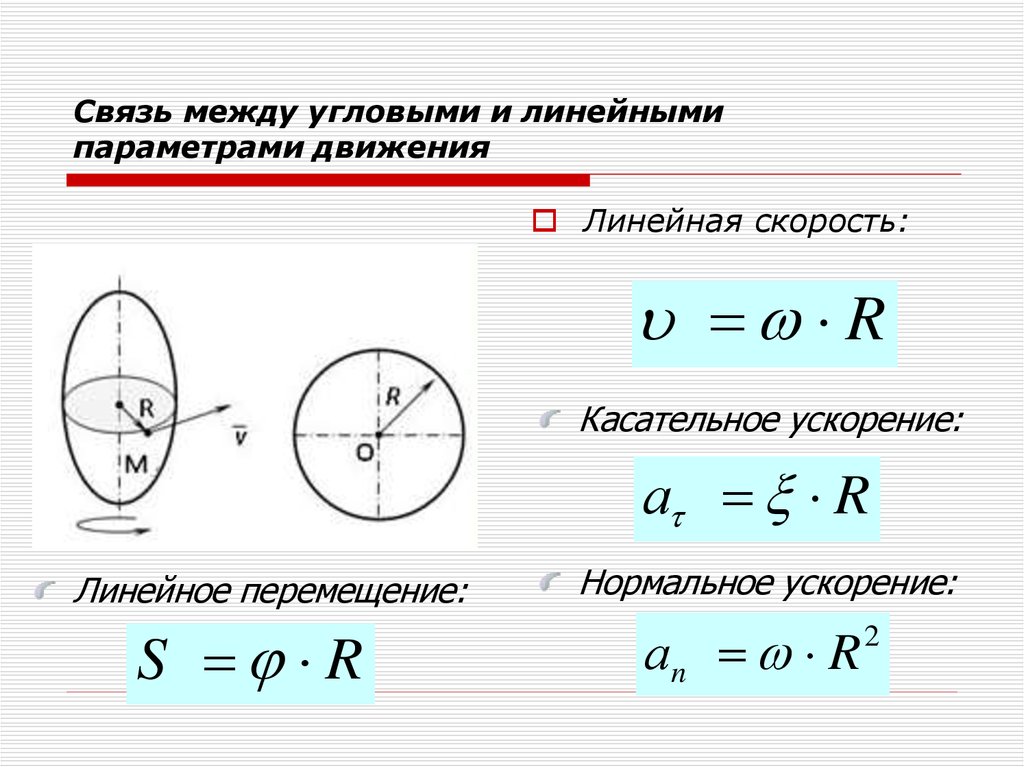
Рассмотрим объект, совершающий равномерное круговое движение в горизонтальной плоскости на поверхности без трения, как показано на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Объект, совершающий равномерное круговое движение по поверхности без трения, вид сверху.
Единственный способ для объекта совершить равномерное круговое движение, как показано, — это если результирующая сила, действующая на объект, направлена к центру круга. Один из способов получить силу, направленную к центру круга, — это прикрепить веревку между центром круга и объектом, как показано на рисунке \(\PageIndex{1}\). Если струна натянута, сила натяжения всегда будет направлена к центру окружности. Таким образом, силы, действующие на объект, равны:
Силы изображены на диаграмме свободного тела, показанной на рисунке \(\PageIndex{2}\) (вид сбоку), где мы также нарисовали вектор ускорения. 2}{R}\\\end{aligned} \] Таким образом, мы находим, что натяжение нити увеличивается пропорционально квадрату скорости и уменьшается пропорционально радиусу окружности.
2}{R}\\\end{aligned} \] Таким образом, мы находим, что натяжение нити увеличивается пропорционально квадрату скорости и уменьшается пропорционально радиусу окружности.
Упражнение \(\PageIndex{1}\)
Рисунок \(\PageIndex{3}\): Возможные траектории (выделены красным), по которым будет следовать блок в случае разрыва строки.
Объект совершает равномерное круговое движение в горизонтальной плоскости, когда внезапно обрывается нить, соединяющая объект с центром вращения. По какому пути пойдет блок после разрыва нити?
Пример \(\PageIndex{1}\)
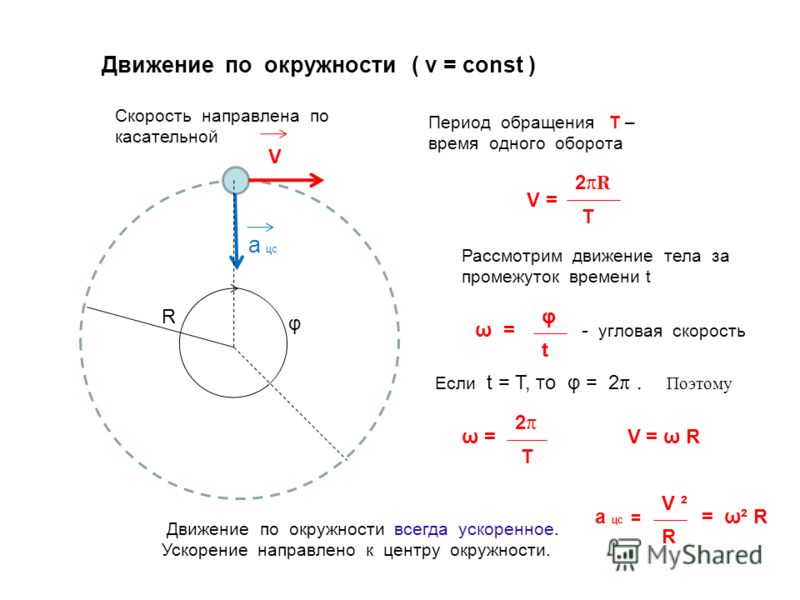
Рисунок \(\PageIndex{4}\): Автомобиль движется по кривой, которую можно аппроксимировать дугой окружности радиусом \(R\).
Автомобиль движется по кривой, которую можно аппроксимировать дугой окружности радиуса \(R\), как показано на рисунке \(\PageIndex{4}\). Коэффициент статического трения между шинами автомобиля и дорогой равен \(µ_{s}\). С какой максимальной скоростью автомобиль может пройти поворот без заноса?
Коэффициент статического трения между шинами автомобиля и дорогой равен \(µ_{s}\). С какой максимальной скоростью автомобиль может пройти поворот без заноса?
Решение :
Если автомобиль движется с постоянной скоростью по кругу, то сумма сил, действующих на автомобиль, должна быть направлена к центру круга. Единственная сила, действующая на автомобиль, которая может быть направлена к центру круга, — это сила трения между шинами и дорогой. Если бы дорога была идеально гладкой (представьте себе вождение в условиях гололеда), было бы невозможно объехать поворот, поскольку не было бы силы трения. Силы на автомобиль:
 При этом происходит этот процесс за время t.
При этом происходит этот процесс за время t.
 2 &\ leq \ mu_s g R \\ \ поэтому v &\ leq \ sqrt {\ mu_s g R} \ end {align} \ ] Таким образом, если скорость меньше \(\sqrt{\mu_s g R}\), автомобиль не будет скользить и величина силы трения покоя, приводящая к ускорению по направлению к центру окружности, будет быть меньше или равно его максимально возможному значению.
2 &\ leq \ mu_s g R \\ \ поэтому v &\ leq \ sqrt {\ mu_s g R} \ end {align} \ ] Таким образом, если скорость меньше \(\sqrt{\mu_s g R}\), автомобиль не будет скользить и величина силы трения покоя, приводящая к ускорению по направлению к центру окружности, будет быть меньше или равно его максимально возможному значению.
 Может ли скорость мяча быть постоянной? Какова минимальная скорость мяча в верхней части круга, если он в состоянии сделать это вокруг круга?
Может ли скорость мяча быть постоянной? Какова минимальная скорость мяча в верхней части круга, если он в состоянии сделать это вокруг круга? Диаграмма свободного тела на рисунке \(\PageIndex{7}\) также показывает векторную сумму веса и напряжения в положении 2 (красная стрелка, обозначенная \(\sum \vec F\)), которая указывает вниз и к слева. Таким образом, очевидно, что вектор ускорения не может быть направлен к центру окружности, и ускорение будет иметь компоненты, которые являются как тангенциальными (\(a_T\)) к окружности, так и радиальными (\(a_R\)), как показано вектором \(\vec a_2\) на рисунке \(\PageIndex{7}\).
Диаграмма свободного тела на рисунке \(\PageIndex{7}\) также показывает векторную сумму веса и напряжения в положении 2 (красная стрелка, обозначенная \(\sum \vec F\)), которая указывает вниз и к слева. Таким образом, очевидно, что вектор ускорения не может быть направлен к центру окружности, и ускорение будет иметь компоненты, которые являются как тангенциальными (\(a_T\)) к окружности, так и радиальными (\(a_R\)), как показано вектором \(\vec a_2\) на рисунке \(\PageIndex{7}\). 2}{R}\\ \поэтому v_{min}&=\sqrt{\frac{gR}{m}}\end{aligned}\] — это минимальная скорость в верхней части траектории, при которой мяч может двигаться по кругу. Натяжение нити будет меняться по мере того, как мяч будет двигаться по кругу, и будет самым высоким в нижней части траектории, поскольку натяжение должно быть больше силы тяжести, чтобы результирующая сила в нижней части траектории была направлена вверх (к центр круга).
2}{R}\\ \поэтому v_{min}&=\sqrt{\frac{gR}{m}}\end{aligned}\] — это минимальная скорость в верхней части траектории, при которой мяч может двигаться по кругу. Натяжение нити будет меняться по мере того, как мяч будет двигаться по кругу, и будет самым высоким в нижней части траектории, поскольку натяжение должно быть больше силы тяжести, чтобы результирующая сила в нижней части траектории была направлена вверх (к центр круга). Если вы укоротите нить, как изменится минимальная угловая скорость (измеренная в верхней части траектории), необходимая для того, чтобы мяч совершил движение по кругу?
Если вы укоротите нить, как изменится минимальная угловая скорость (измеренная в верхней части траектории), необходимая для того, чтобы мяч совершил движение по кругу? Идея использования кривой с наклоном состоит в том, чтобы изменить направление нормальной силы между дорогой и автомобильными шинами так, чтобы она тоже имела составляющую, направленную к центру круга.
Идея использования кривой с наклоном состоит в том, чтобы изменить направление нормальной силы между дорогой и автомобильными шинами так, чтобы она тоже имела составляющую, направленную к центру круга.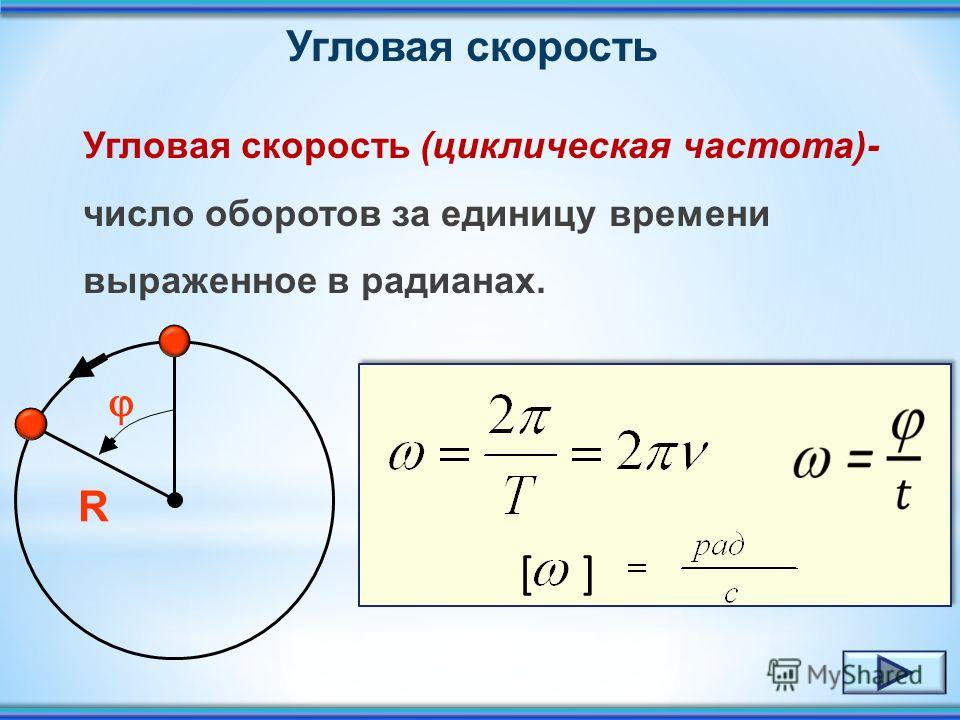 Это статическое трение, потому что поверхность шины не двигается относительно поверхности дороги, если автомобиль не буксует. Сила трения покоя имеет величину не более \(f_s\leq\mu_sN\) и перпендикулярна нормальной силе. Сила может быть направлена либо вверх, либо вниз, , в зависимости от других сил, действующих на автомобиль .
Это статическое трение, потому что поверхность шины не двигается относительно поверхности дороги, если автомобиль не буксует. Сила трения покоя имеет величину не более \(f_s\leq\mu_sN\) и перпендикулярна нормальной силе. Сила может быть направлена либо вверх, либо вниз, , в зависимости от других сил, действующих на автомобиль .

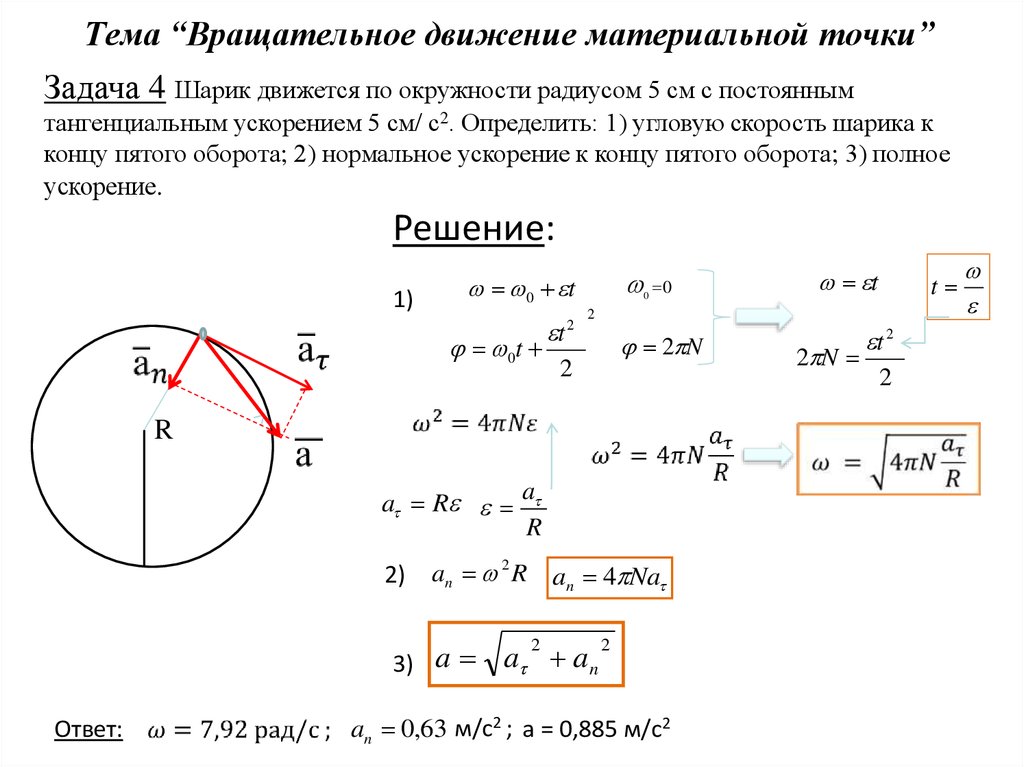 При некоторой максимальной скорости сила трения достигнет своего максимального значения и больше не сможет удерживать ускорение автомобиля, направленное к центру круга. На скоростях ниже идеальной сила трения направлена вверх, чтобы предотвратить скольжение автомобиля по берегу. Если коэффициент статического трения слишком низкий, возможно, что на низких скоростях автомобиль начнет скользить по берегу (поэтому будет минимальная скорость, ниже которой автомобиль начнет скользить вниз). 92}{gR}\\ \therefore v_{ideal} &=\sqrt{gR\tan\theta}\end{aligned}\] При этой скорости сила трения покоя равна нулю. На практике можно использовать это уравнение, чтобы определить, какой угол крена использовать при проектировании дороги, чтобы идеальная скорость была около ограничения скорости или средней скорости движения. Мы оставляем в качестве упражнения определение максимальной скорости, с которой автомобиль может двигаться по кривой, прежде чем выскользнуть из нее.
При некоторой максимальной скорости сила трения достигнет своего максимального значения и больше не сможет удерживать ускорение автомобиля, направленное к центру круга. На скоростях ниже идеальной сила трения направлена вверх, чтобы предотвратить скольжение автомобиля по берегу. Если коэффициент статического трения слишком низкий, возможно, что на низких скоростях автомобиль начнет скользить по берегу (поэтому будет минимальная скорость, ниже которой автомобиль начнет скользить вниз). 92}{gR}\\ \therefore v_{ideal} &=\sqrt{gR\tan\theta}\end{aligned}\] При этой скорости сила трения покоя равна нулю. На практике можно использовать это уравнение, чтобы определить, какой угол крена использовать при проектировании дороги, чтобы идеальная скорость была около ограничения скорости или средней скорости движения. Мы оставляем в качестве упражнения определение максимальной скорости, с которой автомобиль может двигаться по кривой, прежде чем выскользнуть из нее. Это происходит из-за вашей инерции (Первый закон Ньютона), и ваше тело двигалось бы по прямой линии, если бы машина не оказывала на вас суммарной силы по направлению к центру круга. Вы не столько ощущаете силу, толкающую вас наружу, сколько эффект от автомобильного кресла, толкающего вас внутрь; если бы вы прислонились к стороне автомобиля, которая находится снаружи кривой, вы бы почувствовали, как сторона автомобиля толкает вас внутрь к центру кривой, даже если «чувствуется», что вы толкаете наружу против поворота. сторона автомобиля.
Это происходит из-за вашей инерции (Первый закон Ньютона), и ваше тело двигалось бы по прямой линии, если бы машина не оказывала на вас суммарной силы по направлению к центру круга. Вы не столько ощущаете силу, толкающую вас наружу, сколько эффект от автомобильного кресла, толкающего вас внутрь; если бы вы прислонились к стороне автомобиля, которая находится снаружи кривой, вы бы почувствовали, как сторона автомобиля толкает вас внутрь к центру кривой, даже если «чувствуется», что вы толкаете наружу против поворота. сторона автомобиля. 2}{R} &= 0\end{ выровнены}\] что, конечно, математически точно эквивалентно. Сила инерции не является реальной силой в том смысле, что на нее ничто не действует. Это вступает в игру только потому, что мы пытаемся использовать законы Ньютона в неинерциальной системе отсчета. Тем не менее, он обеспечивает хорошую модель для описания ощущения, которое мы испытываем, когда автомобиль выталкивает наружу, когда машина проходит поворот. Иногда люди называют эту силу «центробежной» силой, что означает «сила, направленная от центра». Однако вы должны помнить, что это не реальная сила, действующая на объект, а результат моделирования движения в неинерциальной системе отсчета.
2}{R} &= 0\end{ выровнены}\] что, конечно, математически точно эквивалентно. Сила инерции не является реальной силой в том смысле, что на нее ничто не действует. Это вступает в игру только потому, что мы пытаемся использовать законы Ньютона в неинерциальной системе отсчета. Тем не менее, он обеспечивает хорошую модель для описания ощущения, которое мы испытываем, когда автомобиль выталкивает наружу, когда машина проходит поворот. Иногда люди называют эту силу «центробежной» силой, что означает «сила, направленная от центра». Однако вы должны помнить, что это не реальная сила, действующая на объект, а результат моделирования движения в неинерциальной системе отсчета. Сумма сил часто называется «чистой силой», действующей на объект, а в конкретном случае равномерного кругового движения эту результирующую силу иногда называют «центростремительной силой», однако это не сила. сама по себе, и это всегда сумма сил, направленных к центру круга.
Сумма сил часто называется «чистой силой», действующей на объект, а в конкретном случае равномерного кругового движения эту результирующую силу иногда называют «центростремительной силой», однако это не сила. сама по себе, и это всегда сумма сил, направленных к центру круга.
 Если нить натянута вниз так, что радиус равен половине первоначального радиуса, то закон сохранения углового момента диктует, что мяч должен иметь четырехкратную угловую скорость. Это связано с тем, что произведение момента инерции и угловой скорости должно оставаться постоянным, а уменьшение радиуса вдвое уменьшает момент инерции в четыре раза.
Если нить натянута вниз так, что радиус равен половине первоначального радиуса, то закон сохранения углового момента диктует, что мяч должен иметь четырехкратную угловую скорость. Это связано с тем, что произведение момента инерции и угловой скорости должно оставаться постоянным, а уменьшение радиуса вдвое уменьшает момент инерции в четыре раза.
 Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл.
Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл. Поскольку момент инерции точечной массы определяется как
Поскольку момент инерции точечной массы определяется как