Поисков объектов с пространственным отношением к пересечению—ArcMap

Доступно с лицензией Data Reviewer.

Объекты внутри карты могут пересекаться, например, когда дорога пересекает железную дорогу, или река пересекает дорогу. Проверка пересечения геометрии ищет объекты, находящиеся в пределах заданного допуска пересечения двух других объектов. Например, поиск точек зданий в пределах определенного расстояния от пересечения дорог. Объекты, найденные в пределах допуска, создаются в виде результата с точечным типом геометрии. И наоборот, можно искать объекты, чья точка пересечения выходит за пределы заданного допуска объекта.

Проверка может быть проведена для целого класса пространственных объектов, подтипа, или набора объектов, выбранного с помощью SQL-запроса.

После того как определен критерий проверки, можно настроить примечания и рейтинг степени серьезности. Примечания позволяют уточнять описание для объекта, который был записан в таблицу Reviewer, и копировать их в поле Примечания таблицы Reviewer. Рейтинг степени серьезности позволяет вам отметить степень важности для результатов Reviewer с терминами вашего процесса обеспечения/контроля качества. Чем меньше значение показателя, тем выше приоритет результата проверки.

1. Запустите ArcMap.
2. В главном меню щелкните Настройка > Панели инструментов > Data Reviewer.
3. Щелкните стрелку ниспадающего списка Выбрать проверку данных (Select Data Check) на панели инструментов обозревателя Data Reviewer, щелкните знак плюс (+) рядом с Проверки объекта на объект (Feature on Feature Checks), затем нажмите Проверка пересечения на геометрии (Intersection on Geometry Check).

   Откроется диалоговое окно Свойства проверки пересечения к геометрии (Intersection on Geometry Check Properties).

4. При необходимости введите уникальное имя для проверки в текстовом поле Название проверки.

   Примечание:

   В заголовке можно использовать описание условий, которые находятся с помощью данной проверки. Это может быть полезным, когда есть несколько экземпляров одной проверки для оценки одних и тех же классов пространственных объектов или таблиц, с разными оценочными параметрами.

5. Щелкните стрелку раскрывающегося списка Класс пространственных объектов/Подтип (Feature Class/Subtype) в области Класс пространственных объектов 1 (Feature Class 1) и выберите класс пространственных объектов и подтип, для которых будет запущена проверка.

   Объекты из этого класса пространственных объектов сравниваются с пересечениями между объектами из второго и третьего классов пространственных объектов.

6. Чтобы запустить проверку для целого класса пространственных объектов и сохранить это в настройках, отметьте опцию Всегда запускать для всей базы данных.
7. Чтобы запустить проверку для отдельных объектов в классе пространственных объектов, нажмите SQL для создания SQL-запроса.
8. Повторите шаги 5-7 в областях Класс пространственных объектов 2 (Feature Class 2) и Класс пространственных объектов 3 (Feature Class 3).
9. Если нужно найти объекты, которые не пересекают Класс пространственных объектов 1 (Feature Class 1), поставьте флажок для Не искать объекты, не имеющие пересечений (Not – find features that do not intersect) в области Опция класса пространственных объектов 1 ( Feature Class 1 Option).
10. Укажите значение допуска в текстовом поле Допуск (Tolerance).
11. Щелкните на стрелке ниспадающего списка Единицы измерения (Units) и выберите единицы измерения, которые будут использоваться для допуска.
12. При необходимости введите описание для результатов проверки в текстовом поле Примечания в области примечаний Reviewer.
13. При необходимости щелкните стрелку ниспадающего списка Важность и выберите значение, указывающее на приоритет результатов проверки в области Примечания Reviewer.

    Важность указывает на серьезность результата проверки. Диапазон этих значений от 1 до 5, где 1 обозначает высший приоритет, а 5 — низший.

14. Нажмите ОК.
15. Щелкните кнопку Запустить проверку данных на панели инструментов Data Reviewer.

    Откроется диалоговое окно Объекты для проверки.

16. Выберите опцию в области Объекты для проверки.
    • Выбранный набор – проверка выполняется на объектах, выбранных в данный момент на карте.
    • Текущий экстент – проверка выполняется для текущего экстента карты, управляемого масштабом карты.
    • Определяющий запрос – проверка выполняется на объектах, отображаемых в соответствии с определяющими запросами, которые были созданы для класса пространственных объектов.
    • Вся база данных – проверка выполняется по всем объектам класса пространственных объектов.
17. Чтобы выполнить проверку только на объектах, которые были отредактированы в версионной рабочей области, отметьте Только измененные объекты.

    Примечание:

    Параметр Только измененные объекты доступен только для версионной базы данных.

18. Щелкните ОК.

    Проверка выполняется на экстенте, указанном в диалоговом окне Объекты для оценки.

    После окончания проверки появляется диалоговое окно результатов Reviewer.

19. Вы можете сделать это одним из следующих способов:
    • Если вы хотите просмотреть результаты в окне Просмотр объектов, выберите опцию Просмотр результатов.
    • Если вы начали сеанс Reviewer и хотите записать результаты в таблицу Reviewer, выберите опцию Записать в таблицу Reviewer.
20. Нажмите ОК.

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2 / Хабр

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение

Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости.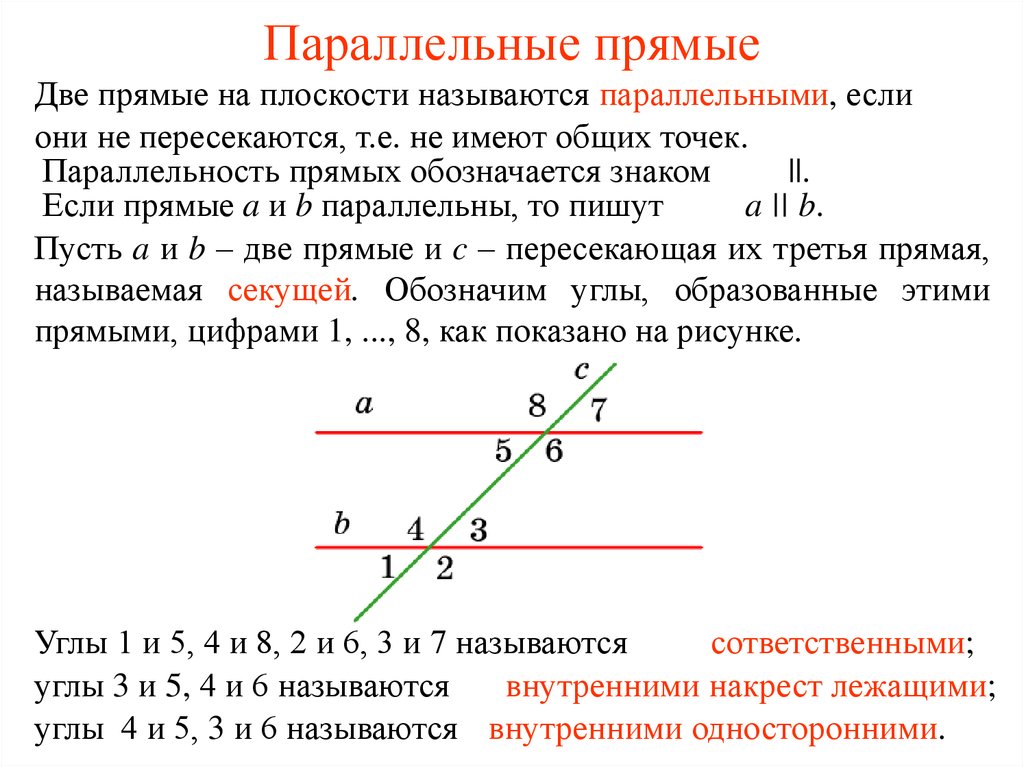 Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение

Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:

1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)

2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение

Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:

1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)

2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение

В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.

Итак:

1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] < 0 – точки лежат по разные стороны.

2. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] > 0 – точки лежат по одну сторону.

3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение

Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.

Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.

Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение

Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] < 0 => [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] < 0. Аналогично

[M₁M₂, M₁P₁] * [M₁M₂, M₁P₂] < 0. Вы наверно думаете, почему не меньше либо равно. А потому, что возможен следующий случай, при котором векторное произведение как раз и равно нулю, но отрезки не пересекаются:

Поэтому нам необходимо сделать еще одну проверку, а именно: принадлежит ли хотя бы один конец каждого отрезка другому (принадлежность точки отрезку). Эту задачу мы уже решали.

Итак, для того чтобы отрезки имели общие точки необходимо и достаточно:

1. Концы отрезков лежат по разные стороны относительно другого отрезка.

2. Хотя бы один из концов одного отрезка принадлежит другому отрезку.

Задача №7

Расстояние от точки до прямой.

Решение

Пусть прямая задана двумя точками P₁(x₁, y₁) и P₂(x₂, y₂).

В предыдущей статье мы говорили о том, что геометрически косое произведение — это ориентированная площадь параллелограмма, поэтому S_P1P2M = 0,5*[P₁P₂, P₁M]. С другой стороны каждому школьнику известна формула для нахождения площади треугольника: половина основание на высоту.

S_P1P2M = 0,5*h*P₁P₂.

Приравнивая эти площади, находим

По модулю взяли потому, что первая площадь ориентированная.

Если же прямая задана уравнением ax + by + c = 0, то уравнение прямой проходящей через точку M перпендикулярной заданной прямой есть: a(y — y₀) – b(x — x₀) = 0. Теперь спокойно можно решить систему из полученных уравнений, найти их точку пересечения и вычислить расстояние от исходной точки до найденной: оно будет ровно ρ = (ax₀ + by₀ + c)/√(a² + b²).

Задача №8

Расстояние от точки до луча.

Решение

Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:

1. (P₁M, P₁P₂) < 0 перпендикуляр не попадает на луч

2. (P₁M, P₁P₂) ≥ 0 перпендикуляр попадает на луч

Задача №9

Расстояние от точки до отрезка.

Решение

Рассуждаем аналогично предыдущей задаче. Если перпендикуляр не падает на отрезок, то ответом будет минимальное из расстояний от данной точки до концов отрезка.

Чтобы определить попадает ли перпендикуляр на отрезок нужно по аналогии с предыдущей задачей использовать скалярное произведение векторов. Если перпендикуляр не падает на отрезок, то либо угол MP₁P₂ либо угол MP₂P₁ будут тупыми. Поэтому по знаку скалярных произведений мы можем определить попадает ли перпендикуляр на отрезок или нет:

Если (P₁M, P₁P₂) < 0 или (P₂M, P₂P₁) < 0 то перпендикуляр не падает на отрезок.

Задача №10

Определить количество точек прямой и окружности.

Решение

Прямая и окружность может иметь нуль, одну или две точки пересечения. Давайте посмотрим на рисунки:

Здесь из рисунков и так все понятно. Мы имеем две точки пересечения, если расстояние от центра окружности до прямой меньше радиуса окружности. Одну точку касания, если расстояние от центра до прямой равно радиусу. И наконец, ни одной точки пересечения, если расстояние от центра окружности до прямой больше радиуса окружности. Поскольку задача нахождения расстояние от точки до прямой была уже нами решена, то и эта задача тоже решена.

Задача №11

Взаимное расположение двух окружностей.

Решение

Возможные случаи расположения окружностей: пересекаются, касаются, не пересекаются.

Рассмотрим случай, когда окружности пересекаются, и найдем площадь их пересечения. Эту задачу я очень люблю, так как потратил на ее решение изрядное количество времени (было это давно — на первом курсе).

Вспомним теперь, что такое сектор и сегмент.

Пересечение кругов состоит из двух сегментов O₁AB и O₂AB.

Казалось бы необходимо сложить площади этих сегментов и все. Однако, все не так просто. Необходимо еще определить всегда ли эти формулы верны. Оказывается, нет!

Рассмотрим случай, когда центр второго круга O₂ совпадает с точкой C. В этом случае d₂ = 0 и за значение α примем α = π. В этом случае имеем полукруг с площадью 1/2 πR₂².

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Надеюсь, Вам понравилось.

sql server 2008 — Почему эта геометрическая точка не пересекается с многоугольником?

спросил
9 лет, 6 месяцев назад

Изменено
9 лет, 6 месяцев назад

Просмотрено
931 раз

Почему эта геометрическая точка не пересекается с многоугольником? Я точно знаю, что точка существует в данном многоугольнике. Любая причина, по которой он возвращает 0?

 ЗАЯВИТЬ геометрию @point
DECLARE @полигеометрия
SET @point = геометрия::STGeomFromText('POINT (-79.393967 43.640056)', 4326)
DECLARE @minY varchar(20) = N'-79.37776573850101'
ОБЪЯВИТЬ @maxY varchar(20) = N'-79.41055306149906'
ОБЪЯВИТЬ @minX varchar(20) = N'43.63590433545648'
ОБЪЯВИТЬ @maxX varchar(20) = N'43.64460037532088'
ОБЪЯВИТЬ @boundingRect varchar (250)
SET @boundingRect = 'POLYGON((' + @minX + ' ' + @minY + ', ' +
                                                   @maxX + ' ' + @minY + ', ' +
                                                   @maxX + ' ' + @maxY + ', ' +
                                                   @minX + ' ' + @maxY + ', ' +
                                                   @minX + ' ' + @minY + '))'
SET @poly = геометрия::STGeomFromText(@boundingRect, 4326)
ВЫБЕРИТЕ @point. STIntersects(@poly)
 

• sql-server-2008
• пространственный
• sqlgeography

1

Я не знаком с этой нотацией SQL, поэтому я могу ошибаться, но я вижу, что ваши значения X, кажется, связаны с широтой 43N, а Y с долготой 79W. Однако ваши записи POINT могут быть отменены?

Просто мысль: когда точка пересекается с многоугольником? Если он лежит ВНУТРИ полигона? Нет. Только если он лежит прямо на одном из ребер многоугольника, верно?
Попробуйте следующее: Пересеките точку с многоугольником, которая лежит непосредственно на одном из ребер многоугольника. Если он возвращает else, то 0, у вас есть ответ.

Точка должна быть объявлена ​​как:

 SET @point = геометрия::STGeomFromText('POINT (43.640056 -79.393967)', 4326)
 

Затем Intersect показывает ожидаемый результат: 1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Параллельные линии (геометрия) | Brilliant Math & Science Wiki

Содержание

• Основные свойства параллельных линий
• Обходы параллельных линий

Параллельные прямые никогда не пересекаются. На языке линейных уравнений это означает, что они имеют одинаковый наклон. Другими словами, при некотором изменении независимой переменной каждая строка будет иметь идентичное друг другу изменение зависимой переменной.

В трехмерном пространстве параллельные линии — это (неподвижные) линии, лежащие в одной плоскости и не пересекающиеся. Важно отметить, что некоторые другие линии в трехмерном пространстве могут не пересекаться, но и не лежать в одной плоскости; они известны как наклонные линии.

Imgur

На этом рисунке добавлена ​​поперечная (линия PQ↔\overleftrightarrow{PQ}PQ​). Пусть XXX и YYY будут точками пересечения секущей с AB↔\overleftrightarrow{AB}AB и CD↔,\overleftrightarrow{CD},CD соответственно. Теперь, учитывая, что AB↔∥CD↔,\overleftrightarrow{AB}\parallel\overleftrightarrow{CD},AB∥CD, всегда следует, что ∠PXB=∠PYD.\angle PXB=\angle PYD.∠PXB=∠PYD . Углы в этом виде отношений известны как соответствующие углы . Обратите внимание, что ∠PXB=∠AXY,\угол PXB=\угол AXY,∠PXB=∠AXY, так как они являются противоположными углами. Тогда мы имеем ∠AXY=∠XYD,\угол AXY=\угол XYD,∠AXY=∠XYD, которые называются альтернативными углами .

Обратные свойства вышеприведенных также верны. Если две прямые имеют соответствующие углы, то эти две прямые параллельны. Кроме того, если две прямые имеют альтернативные углы, то мы можем сказать, что эти две прямые параллельны.

Изображение

Теперь представьте, что вы рисуете поперечную (линия PQ↔\overleftrightarrow{PQ}PQ​), которая пересекается перпендикулярно двум параллельным линиям, как показано на рисунке выше. Тогда длина XY‾\overline{XY}XY будет кратчайшим расстоянием между двумя параллельными прямыми. Теперь мы проводим дополнительную секущую (прямая P′Q′↔\overleftrightarrow{P’Q’}P’Q′​), которая также перпендикулярно пересекается с двумя параллельными прямыми. Обратите внимание, что PQ↔\overleftrightarrow{PQ}PQ​ и P′Q′↔\overleftrightarrow{P’Q’}P′Q′​ параллельны (попробуйте доказать это, используя понятие соответствующих углов и альтернативных углов!). Теперь у нас также есть длина P′Q′‾\overline{P’Q’}P′Q′​ как кратчайшее расстояние между двумя параллельными прямыми, и, следовательно, верно, что ∣PQ‾∣=∣P′Q ′‾∣.\lvert\overline{PQ}\rvert=\lvert\overline{P’Q’}\rvert.∣PQ​∣=∣P′Q′​∣. Это означает, что две параллельные линии всегда находятся на постоянном расстоянии друг от друга, что является еще одной важной характеристикой параллельных линий.

Рассуждая более интуитивно, это должно быть правдой, поскольку, если бы линии отдалялись друг от друга, то на противоположной стороне линии сближались бы (и, в конце концов, встречались), что противоречит определению, согласно которому две параллельные линии никогда не встретиться. Обратите внимание, что расстояние между двумя отдельными линиями можно определить, только если линии параллельны. Если линии не параллельны, то расстояние будет продолжать изменяться.

Обсуждение чуть выше, к вашему сведению, на самом деле соответствует Пятый постулат Евклида , или параллельный постулат . Он гласит, что если отрезок пересекает две прямые линии, образующие два внутренних угла на одной стороне, сумма которых меньше 180 градусов, то две прямые, если их продолжить на неопределенный срок, пересекутся на той стороне, на которой сумма углов меньше 180 градусов. . Другими словами, две прямые параллельны, если сумма внутренних углов на одной стороне равна ровно 180 градусам.

Итак,

• Углы, лежащие на одной и той же стороне секущей и между параллелями (называемые соответственными углами), равны. Верно и обратное: если две прямые имеют равные соответствующие углы, то прямые параллельны.

• Углы, лежащие на противоположных сторонах секущей и между параллелями (называемые параллельными углами), равны. Верно и обратное: если противоположные углы равны, прямые параллельны.

• Две параллельные прямые находятся на постоянном расстоянии друг от друга, поэтому любая пара прямых, пересекающих их под одним и тем же углом, образует отрезки одинаковой длины.

Если на следующей диаграмме отрезки QUQUQU и RTRTRT параллельны, что мы можем сказать об углах PVQPVQPVQ и TWSTWSTWS?

---

У нас есть

∠PVQ=∠PWR (соответствующие углы) =∠TWS. (противоположные углы)  \begin{array} { l l l } \angle PVQ & = \angle PWR & \text{ (соответствующие углы) } \\ & = \angle TWS. & \text{ (противоположные углы) } \\ \end{массив} ∠PVQ​=∠PWR=∠TWS.​ (соответствующие углы)  (противоположные углы) ​

Следовательно, эти углы равны. □ _\квадрат □​

Изображение 9\circ.x=45∘+65∘=110∘. □_\квадрат□​

Имгур

На рисунке выше две линии XY↔\overleftrightarrow{XY}XY и AD↔\overleftrightarrow{AD}AD параллельны. Если площадь △ABY\треугольника ABY△ABY равна 5, то какова площадь △CDX?\треугольника CDX?△CDX?

---

Поскольку XY↔\overleftrightarrow{XY}XY и AD↔\overleftrightarrow{AD}AD параллельны, высоты двух треугольников будут равны.