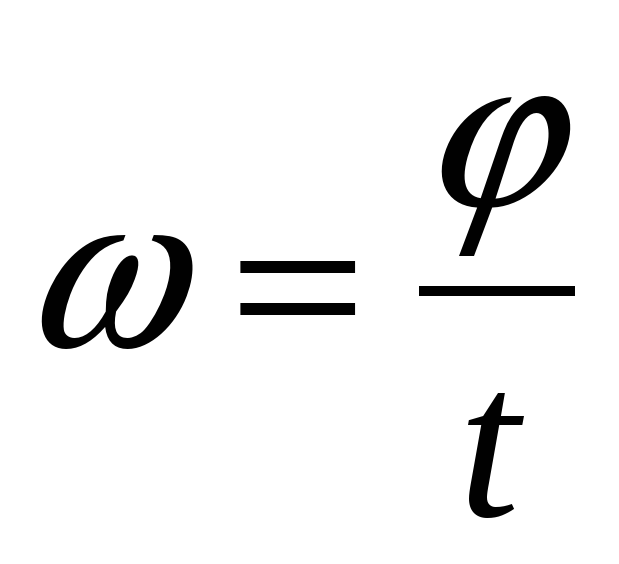Равномерное движение по окружности | Физика

1. Основные характеристики равномерного движения по окружности

Движение по окружности часто встречается в природе и технике: по траекториям, близким к окружностям, движутся планеты вокруг Солнца, Луна и искусственные спутники Земли, точки колес и вращающихся деталей механизмов.

Мы ограничимся в нашем курсе равномерным движением по окружности. Напомним, что равномерным называют движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.

Каковы же основные характеристики равномерного движения по окружности?

Прежде всего, это радиус окружности r и модуль скорости тела v (рис. 8.1). Далее мы увидим, что мгновенная скорость в каждой точке траектории направлена по касательной к траектории.

Следующей характеристикой равномерного движения по окружности является период обращения T. Он равен промежутку времени, в течение которого тело совершает один оборот.

? 1. Во сколько раз период обращения секундной стрелки меньше периода обращения часовой стрелки?

? 2. Докажите, что период обращения T, радиус окружности r и модуль скорости тела v связаны соотношением

T = 2πr/v. (1)

Частотой обращения ν называют число оборотов за единицу времени (секунду). Значение частоты не всегда целое число: например, если тело совершает 10 оборотов в секунду, то ν = 10 с^-1, а если оно совершает пол-оборота в секунду, то ν = 0,5 с^-1.

Чем больше частота обращения, тем меньше период.

? 3. Докажите, что период T и частота обращения ν связаны соотношением

ν = 1/T (2).

? 4. Чему равна частота обращения секундной стрелки, ми- К. нутной стрелки, часовой стрелки, Земли при ее суточном вращении и при ее движении вокруг Солнца?

2. Направление мгновенной скорости при движении по окружности

Поставим опыт
Затачивая инструмент с по: мощью точильного круга, можно заметить, что искры летят по касательной к кругу в точке, которой касается инструмент (рис. 8.2). Это раскаленные кусочки, оторвавшиеся от круга, поэтому их скорость в момент отрыва равна (по модулю и направлению) скорости точек диска, соприкасающихся с инструментом.

Этот опыт показывает, что при движении по окружности мгновенная скорость тела v_vec направлена по касательной к окружности в точке, где в данный момент находится тело.

Чтобы лучше осознать это, рассмотрим движение тела в течение времени Δt, малого по сравнению с периодом T. Пройденная за это время дуга окружности почти сливается с участком касательной к окружности (эта касательная показана голубой линией на рис. 8.3). А это как раз и означает, что мгновенная скорость тела направлена по касательной.

Заметим, что касательная к окружности в некоторой точке перпендикулярна радиусу окружности, проведенному в эту точку. Следовательно,
при движении по окружности мгновенная скорость тела v_vec направлена перпендикулярно радиусу, проведенному в точку, где находится тело в данный момент (см. рис. 8.1).

? 5. На рисунке 8.4 изображена траектория тела, движущегося по окружности. Перенесите рисунок в тетрадь и отметьте на нем:
а) вектор скорости тела, когда оно находится в точках А и В;
б) точку С, в которой скорость тела составляет угол 45º со скоростью тела в момент, когда оно находится в точке А.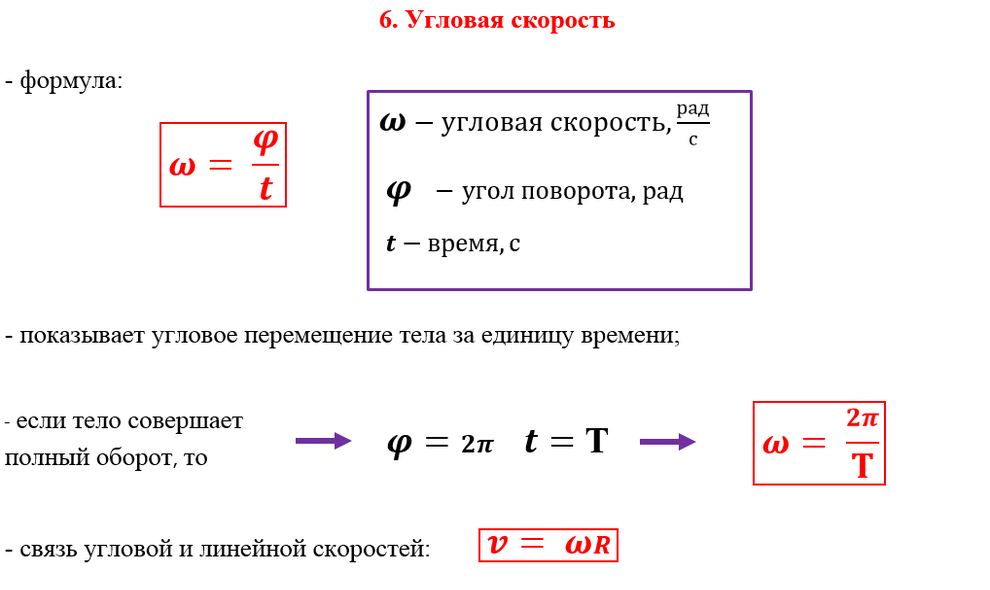

3. Ускорение при равномерном движении по окружности

Поскольку мгновенная скорость тела направлена по касательной в каждой точке траектории, направление скорости тела при его движении по окружности изменяется. А если скорость тела изменяется любым образом (пусть даже только по направлению), то это тело движется с ускорением. Итак, при равномерном движении по окружности тело движется с ускорением.

Докажем, что
при равномерном движении тела со скоростью v по окружности радиуса r:
а) ускорение тела в каждый момент времени направлено по радиусу к центру окружности,
б) модуль ускорения a = v2/r.

Направление ускорения

Поскольку

направление вектора ускорения совпадает с направлением вектора изменения скорости Δ.

Найдем изменение скорости Δ за промежуток времени Δt, малый по сравнению с периодом T.
Обозначим ₁ скорость тела в момент времени t, а ₂ скорость тела в момент времени t + Δt. Тогда

Δ =₂ – ₁.

Обозначим Δα угол, на который повернется за время Δt радиус, проведенный в точку, где находится тело (рис. 8.5, а). Угол Δα мал, если Δt мало по сравнению с T.

На такой же угол Δα повернется за время Δt и вектор скорости тела (скорость остается все время перпендикулярной радиусу).

На рисунке 8.5, б показано, как найти изменение скорости Δ.

Векторы ₁, ₂ и Δ образуют равнобедренный треугольник с основанием Δ и малым углом Δα при вершине. Поэтому углы при основании этого треугольника близки к прямым углам (это следует из того, что сумма углов треугольника 180º).

Значит, изменение скорости Δ за очень малое время Δt направлено перпендикулярно скорости, то есть по радиусу, причем к центру окружности, как показано на рисунке 8.5, в. Ускорение направлено так же, как изменение скорости Δ, следовательно, ускорение тела направлено к центру окружности.

По этой причине ускорение тела при его движении по окружности часто называют центростремительным.

Из курса физики основной школы вы уже знаете, что ускорение тела обусловлено действующими на него силами. Например, при движении Земли вокруг Солнца силой, вызывающей центростремительное ускорение Земли, является сила тяготения со стороны Солнца.

? 6. Автомобиль поворачивает на 90º по дуге окружности. Изобразите на чертеже в тетради векторы скорости и ускорения автомобиля в середине дуги поворота.

Модуль ускорения

За промежуток времени Δt тело, движущееся со скоростью v, проходит по дуге окружности путь Δl = v * Δt (это красная сплошная линия на рисунке 8.6, а).

Если Δt мало по сравнению с T, эта дуга почти не отличается от отрезка прямой. Поэтому фигура, образованная двумя радиусами r и этим отрезком, представляет собой равнобедренный треугольник с основанием Δl = v * Δt.

Этот треугольник подобен равнобедренному треугольнику, образованному скоростями Δ₁, Δ₂ и изменением скорости Δ = * Δt (он изображен на рисунке 8.6, б), поскольку углы при вершинах этих треугольников равны.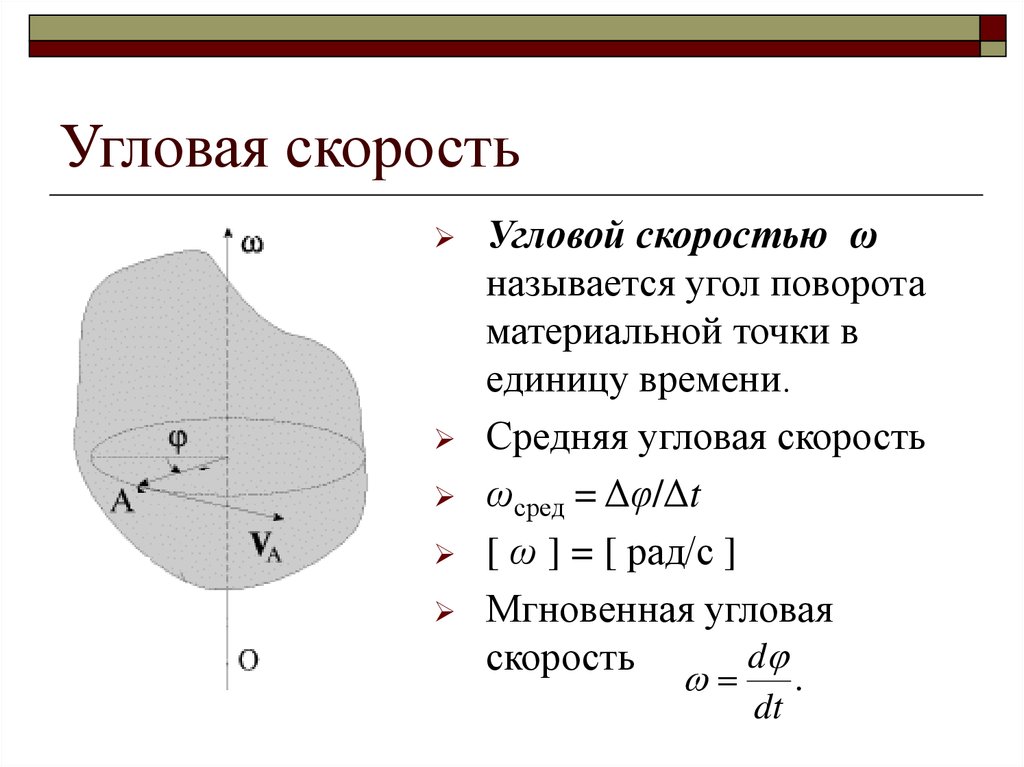 Следовательно, основания указанных двух треугольников относятся, как их боковые стороны:

(a * Δt) / (v * Δt) = v/r,

откуда получаем:

a = v2/r, (4)

Центростремительное ускорение можно выразить также через ν и r или через T и r.

? 7. Докажите, что центростремительное ускорение выражается также формулами

Подсказка. Воспользуйтесь формулами (4), (1), (2).

Можно подумать, что центростремительное ускорение, обусловленное изменением только направления скорости, не может быть значительным. Убедимся, что это не всегда так.

? 8. Чтобы космонавты без вреда для здоровья переносили большие перегрузки во время старта и посадки космического корабля, их тренируют с помощью специального аппарата – огромной центрифуги (рис. 8.7). Во время тренировки в Центре подготовки космонавтов им. Ю. А. Гагарина космонавт движется в капсуле (она изображена в левой части фотографии) по окружности радиусом 18 м.

а) С каким ускорением движется космонавт, когда центрифуга делает шесть оборотов в минуту?
б) При какой частоте обращения космонавт движется с ускорением, превышающим ускорение свободного падения в 10 раз? Чему равна при этом его линейная скорость?

Чтобы испытать на себе ощущения при движении с ускорением, в несколько раз превышающем ускорение свободного падения, можно покататься на центрифуге в парке (рис. 8.8).

? 9. Радиус колеса аттракциона 10 м. Чему равен период его обращения, когда пассажиры движутся с ускорением, в 2,5 раза превышающим ускорение свободного падения?

4. Угловая скорость

Иногда используют еще одну характеристику равномерного движения по окружности – угловую скорость ω. Ее определяют соотношением

ω = Δα/t,

где Δα – угол, на который за время t поворачивается радиус, проведенный к телу из центра окружности (рис. 8.9).

При атом угол измеряют в радианах, то есть одному полному обороту соответствует поворот на угол 2π. Единица угловой скорости совпадает с единицей частоты (1 с^-1). (Напомним, что один радиан (рад) равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности; 1 рад ≈ 57º.)

? 10. Какая скорость одинакова для всех точек минутной стрелки – линейная или угловая?

? 11. Во сколько раз угловая скорость секундной стрелки больше угловой скорости минутной стрелки?

? 12. Докажите, что угловая скорость связана с периодом обращения, частотой, радиусом окружности и скоростью соотношениями

ω = 2π/T, (7)
ω = 2πν, (8)
v = ωr. (9)

? 13.Чему равна угловая скорость движения точки поверхности Земли, обусловленная суточным вращением? Одинакова ли эта скорость для всех точек земной поверхности, находящихся: а) на одной параллели; б) на одном меридиане; в) на различных параллелях и меридианах?

? 14. Докажите, что центростремительное ускорение выражается через угловую скорость и радиус окружности формулой

a = ω2r. (10)

5. Катящееся колесо

Рассмотрим движение различных точек колеса автомобиля.

Пусть автомобиль едет со скоростью (рис. 8.10), причем его колеса катятся без проскальзывания.

Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют четкие следы). Этот факт – отправная точка для нахождения скорости всех других точек колеса – например, точек В, С, D на рисунке 8. 10.

Чтобы найти скорость этих точек, удобно перейти в систему отсчета, связанную с автомобилем, а потом вернуться в систему отсчета, связанную с дорогой.

В системе отсчета, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим v_вр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля v и скорость вращения v_вр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.
Заметим, что скорость _Aвр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).

Выразим через v и v_вр скорость v_А точки А в системе отсчета, связанной с дорогой. Согласно правилу сложения скоростей скорость точки А относительно дороги

A = _Aвр + .

Итак, скорости _Aвр и направлены противоположно, а их сумма _A = 0.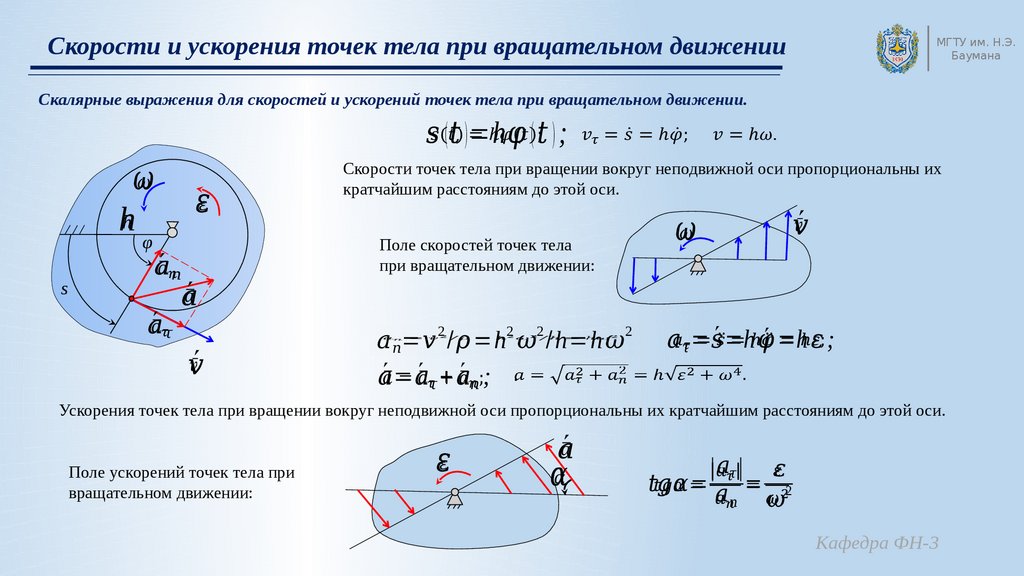 Следовательно,

v_вр = v,

то есть скорость движения точек обода колеса в системе отсчета, связанной с автомобилем, равна но модулю скорости автомобиля.

? 15.Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2v.

? 16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.

? 17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью v = u(R/(R+r)).

Подсказка. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.

? 18.С какой скоростью v и в каком направлении будет двигаться катушка в случае, изображенном на рисунке 8.14?

Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.

? 19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.

Подсказка. Перейдите в систему отсчета, связанную с велосипедистом.

Дополнительные вопросы и задания

Необходимые для решения задач справочные данные, не приведенные в условии задачи, вы можете найти в конце учебника (под обложкой).

20. Длина минутной стрелки настенных часов 15 см, а часовой стрелки – 10 см. Какие величины можно определить из этого условия? Чему они равны?

21. Чему равна обусловленная суточным вращением скорость точек поверхности Земли, расположенных на экваторе? Длину экватора примите равной 40000 км.

22. Две шестеренки сцеплены, как показано на рисунке 8.16. Радиусы шестеренок 60 см и 30 см. Большая шестеренка вращается с частотой 2 с^-1.

а) С какой скоростью движутся зубцы большой шестеренки?
б) По часовой стрелке или против нее движутся зубцы маленькой шестеренки? С какой скоростью они движутся?
в) Чему равна частота обращения маленькой шестеренки?

23. Диск радиусом 2 м равномерно вращается вокруг своей оси с периодом 0,5 с. Начертите графики зависимости скорости v и ускорения a точки диска от расстояния r до центра диска.

24. Наблюдения колец Сатурна (рис. 8.17) показали, что чем дальше от планеты находится участок кольца, тем меньше его скорость. Могут ли кольца Сатурна быть сплошными? Обоснуйте свой ответ.

Самолет летит вдоль 60-й параллели. Во время всего полета его пассажиры наблюдают Солнце в одной и той же точке небосвода. Длину экватора примите равной 40000 км.
а) В каком направлении летит самолет?
б) За какое время он совершит полный круг?
в) Какой путь самолет пролетит за это время?
г) С какой скоростью летит самолет?

26. Два тела равномерно движутся по окружностям радиусом 10 см и 1 м соответственно. У какого тела ускорение больше и во сколько раз, если:
а) скорости тел равны?
б) периоды обращения тел равны?

27. Во сколько раз ускорение точек земной поверхности на экваторе меньше ускорения свободного падения g? Во сколько раз надо было бы уменьшить продолжительность суток, чтобы оно стало равным g?

2.

Кинематические характеристики вращательного движения вокруг неподвижной оси: угловая скорость, угловое ускорение.

Вопросы к экзамену
по физике
(ч. I,
2011 г).

1. Кинематика
   поступательного движения. Системы
   отсчета. Траектория, длина пути,
   перемещение. Скорость и ускорение.
   Средняя, средняя путевая, мгновенная
   скорость. Нормальное, тангенциальное
   и полное ускорение.

2. Кинематические
   характеристики вращательного движения
   вокруг неподвижной оси: угловая
   скорость, угловое ускорение.

3. Динамика
   поступательного движения. Законы
   Ньютона. (Савельев И.В. Т.1 § 7, 9, 11).
   Основные физические величины и их
   размерности. (Савельев И.В. Т.1 § 10).
   Виды сил в механике. (Савельев И.В. Т.1
   § 13–16).

4. Кинетическая и
   потенциальная энергия. Механическая
   работа и мощность. Консервативные и
   неконсервативные силы. Работа в поле
   этих сил. Закон сохранения энергии.

5. Импульс механической
   системы. Закон сохранения импульса.

6. Момент силы
   относительно точки и относительно оси
   вращения.

7. Момент импульса
   материальной точки относительно точки
   и относительно оси вращения. Момент
   импульса тела относительно оси. Закон
   сохранения момента импульса.

8. Основной закон
   динамики вращательного движения.
   Моменты инерции однородных тел
   правильной геометрической формы.
   Теорема Штейнера о параллельных осях.

9. Кинетическая
   энергия, работа и мощность при
   вращательном движении. Сопоставление
   основных формул и законов поступательного
   и вращательного движения.

10. Кинематика
    гармонических колебаний. Величины,
    характеризующие гармонические
    колебания: период, частота, амплитуда,
    фаза. Связь между периодом колебаний
    и циклической частотой. Зависимости
    смещения, скорости и ускорения от
    времени. Соответствующие графики.

11. Уравнение
    гармонических колебаний в дифференциальной
    форме. Зависимость смещения от времени.
    Связь между циклической частотой и
    массой колеблющейся точки. Энергия
    гармонических колебаний (кинетическая,
    потенциальная и полная). Соответствующие
    графики.

12. Математический
    и физический маятники. Формулы для
    периода малых колебаний. (Савельев
    И.В. Т.1 § 54).

13. Сложение
    гармонических колебаний одинакового
    направления и одинаковой частоты.
    Векторная диаграмма. (Савельев Т.1 §
    55).

14. Затухающие
    колебания. Уравнение затухающих
    колебаний в дифференциальной форме.
    Зависимость смещения и амплитуды
    затухающих колебаний от времени.
    Коэффициент затухания. Логарифмический
    декремент колебаний. (Савельев И.В. Т.1
    § 58).

15. Вынужденные
    колебания. Уравнение вынужденных
    колебаний в дифференциальной форме.
    Смещение, амплитуда и частота вынужденных
    колебаний. Явление резонанса. График
    зависимости амплитуды от частоты.

16. Волны. Распространение
    волн в упругой среде. Поперечные и
    продольные волны. Фронт волны и волновые
    поверхности. Длина волны. Уравнение
    бегущей волны. (Савельев Т.2 § 93-95).

17. Образование
    стоячих волн. Уравнение стоячей волны.
    Амплитуда стоячей волны. (Савельев
    И.В. Т.2 § 99)

18. Два подхода к
    изучению макросистем: молекулярно-кинетический
    и термодинамический. Основные параметры
    макросистем. Уравнение состояния
    идеального газа (уравнение
    Клапейрона-Менделеева). (Савельев И.В.
    Т.1 § 79–81, 86).

19. Уравнение состояния
    реального газа (уравнение Ван-дер-Ваальса).
    Теоретическая изотерма Ван-дер-Ваальса
    и экспериментальная изотерма реального
    газа. Критическое состояние вещества.
    (Савельев И.В. Т.1 § 91, § 123–124).

20. Внутренняя энергия
    системы. Внутренняя энергия идеального
    газа. Два способа изменения внутренней
    энергии. Количество теплоты. Теплоемкость.
    Связь удельной и молярной теплоемкостей.

21. Работа при изменении
    объема. Первое начало термодинамики.
    Формула Майера. Применение первого
    начала термодинамики к изопроцессам
    идеального газа.

22. Классическая
    теория теплоемкости идеального газа.
    Теорема Больцмана о равномерном
    распределении энергии по степеням
    свободы молекулы. Вычисление внутренней
    энергии идеального газа и его
    теплоемкостей через число степеней
    свободы. (Савельев И.В. Т.1 § 97).

23. Применение первого
    начала термодинамики к адиабатическому
    процессу. Уравнение Пуассона. (Савельев
    И.В. Т.1 § 88).

1.
Кинематика
поступательного движения. Системы
отсчета. Траектория, длина пути,
перемещение. Скорость и ускорение.
Средняя, средняя путевая, мгновенная
скорость. Нормальное, тангенциальное
и полное ускорение.

Кинематика
поступательного движения

При поступательном
движении тела все точки тела движутся
одинаково, и, вместо того чтобы
рассматривать движение каждой точки
тела, можно рассматривать движение
только одной его точки.

Основные
характеристики движения материальной
точки: траектория движения, перемещение
точки, пройденный ею путь, координаты,
скорость и ускорение.

Линию, по которой
движется материальная точка в
пространстве, называют траекторией.

Перемещением материальной
точки за некоторый промежуток времени
называется вектор перемещения ∆r=r-r₀,
направленный от положения точки в
начальный момент времени к ее положению
в конечный момент.

Скорость материальной
точки представляет собой вектор,
характеризующий направление и быстроту
перемещения материальной точки
относительно тела отсчета. Вектор
ускорения характеризует
быстроту и направление изменения
скорости материальной точки относительно
тела отсчета.

Средняя скорость —
векторная физическая величина равная
отношению вектора перемещения к
промежутку времени, за который происходит
это перемещение:

Мгновенная скорость —
векторная физическая величина, равная
первой производной от
радиус-вектора по времени:

Мгновенная
скорость v есть
векторная величина, равная первой
производной радиуса — вектора движущейся
точки по времени. Так как секущая в
пределе совпадает с касательной,
то вектор
скорости v направлен
по касательной к
траектории в сторону движения (рисунок
1. 2).

По мере уменьшение
∆t путь ∆S все больше будет приближаться
к |∆r|, поэтому модуль
мгновенной скорости:

Нормальное
ускорение –
это составляющая вектора ускорения,
направленная вдоль нормали к траектории
движения в данной точке на траектории
движения тела. То есть вектор нормального
ускорения перпендикулярен линейной
скорости движения (см. рис. 1.10). Нормальное
ускорение характеризует изменение
скорости по направлению и обозначается
буквой а_n.
Вектор нормального ускорения направлен
по радиусу кривизны траектории.

Тангенциальное
(касательное) ускорение –
это составляющая вектора ускорения,
направленная вдоль касательной к
траектории в данной точке траектории
движения. Тангенциальное ускорение
характеризует изменение скорости по
модулю при криволинейном движении.

Полное
ускорение при
криволинейном движении складывается
из тангенциального и нормального
ускорений по правилу
сложения векторов и
определяется формулой:

(согласно
теореме Пифагора для прямоугольно
прямоугольника).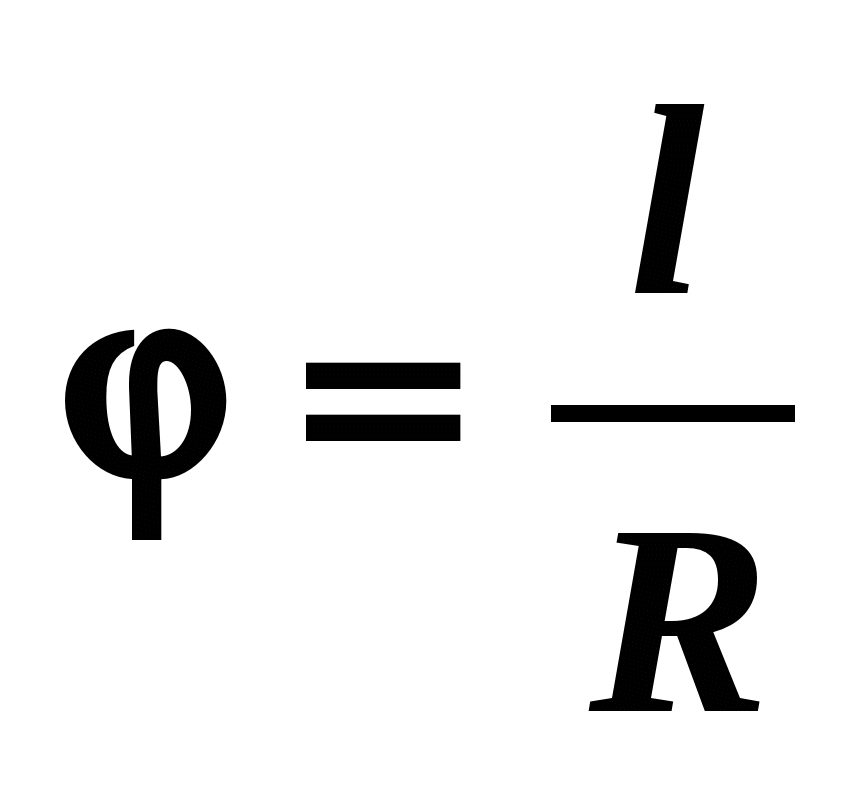

Направление
полного ускорения также определяется правилом
сложения векторов:

а=
а_τ
+ а_n

Ускорение –
это величина, которая характеризует
быстроту изменения скорости.

Например,
автомобиль, трогаясь с места, увеличивает
скорость движения, то есть движется
ускоренно. Вначале его скорость равна
нулю. Тронувшись с места, автомобиль
постепенно разгоняется до какой-то
определённой скорости. Если на его пути
загорится красный сигнал светофора,
то автомобиль остановится. Но остановится
он не сразу, а за какое-то время. То есть
скорость его будет уменьшаться вплоть
до нуля – автомобиль будет двигаться
замедленно, пока совсем не остановится.
Однако в физике нет термина «замедление».
Если тело движется, замедляя скорость,
то это тоже будет ускорение тела, только
со знаком минус (как вы помните, скорость –
это векторная величина).

Среднее
ускорение>
– это отношение изменения скорости к
промежутку времени, за который это
изменении произошло. Определить среднее
ускорение можно формулой:

где a – вектор
ускорения.

Направление
вектора ускорения совпадает с направлением
изменения скорости ΔV = V — V₀ (здесь ₀ –
это начальная скорость, то есть скорость,
с которой тело начало ускоряться).

В момент времени
t1 (см. рис 1.8) тело имеет скорость V₀.
В момент времени t2 тело имеет скорость V.
Согласно правилу вычитания векторов
найдём вектор изменения скорости
ΔV = V — V₀ 
Тогда определить ускорение
можно так:

Рис.
1.8. Среднее ускорение.

В СИ единица
ускорения –
это 1 метр в секунду за секунду (или метр
на секунду в квадрате), то есть

Метр на секунду
в квадрате равен ускорению прямолинейно
движущейся точки, при котором за одну
секунду скорость этой точки увеличивается
на 1 м/с. Иными словами, ускорение
определяет, насколько изменяется
скорость тела за одну секунду. Например,
если ускорение равно 5 м/с²,
то это означает, что скорость тела
каждую секунду увеличивается на 5 м/с.

Можно также
ввести среднюю
скорость по перемещению,
которая будет вектором,
равным отношению перемещения ко
времени, за которое оно совершено:

Средняя скорость,
определённая таким образом, может
равняться нулю даже в том случае, если
точка (тело) реально двигалась (но в
конце промежутка времени вернулась в
исходное положение).

Если перемещение
происходило по прямой (причём в одном
направлении), то средняя путевая скорость
равна модулю средней скорости по
перемещению.

Движение тел
происходит в пространстве и во времени.
Поэтому для описания движения материальной
точки надо знать, в каких местах
пространства эта точка находилась и в
какие моменты времени она проходила
то или иное положение.

Тело отсчета —
произвольно выбранное тело, относительно
которого определяется положение
остальных тел.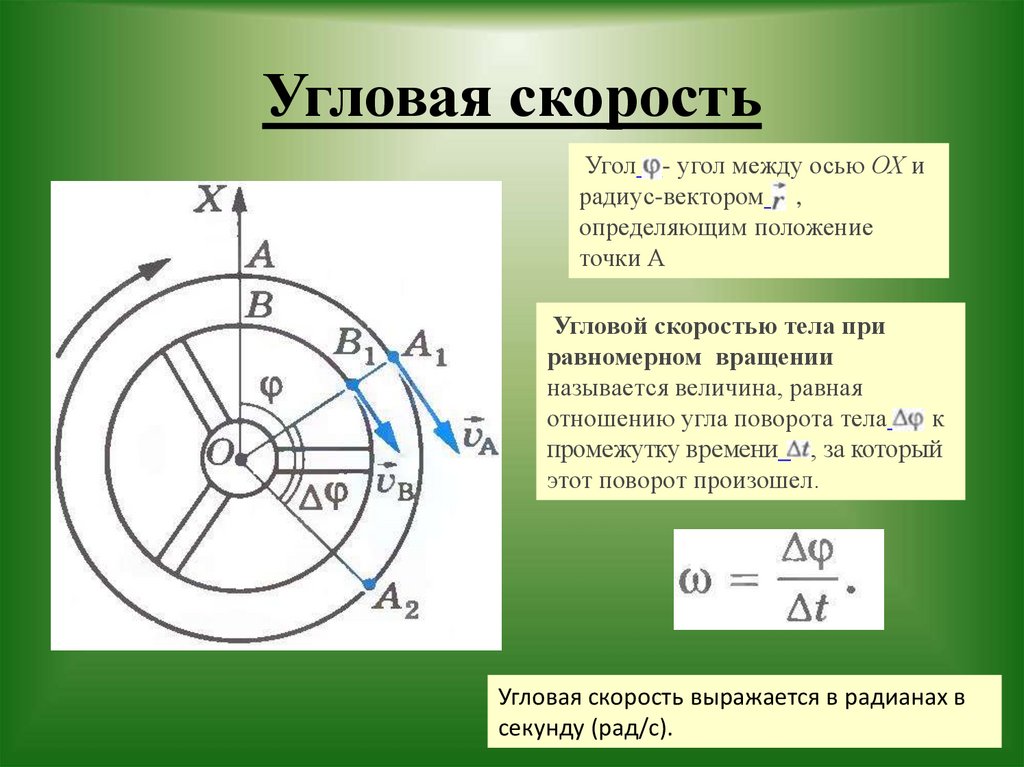

Система
отсчета —
совокупность системы координат и часов,
связанных с телом отсчета.

Наиболее
употребительная система координат
— декартовая —
ортонормированный базис которой
образован тремя единичными по модулю
и взаимно ортогональными векторами i
j k r
r r ,
, ,
проведенными из начала координат.

Положение
произвольной
точки M характеризуется радиусом-вектором Rr ,
соединяющим начало координат O с
точкой M . r
x i y j z k r
r r r = + + , r = r = x2 + y2+ z2 r

Движение материальной
точки полностью определено, если
декартовы координаты материальной
точки заданы в зависимости от времени:
x = x(t) y = y(t) z =z(t)

Эти уравнения
называются кинематическими
уравнениями движения точки.
Они эквивалентны одному векторному
уравнению движения точки.

Линия, описываемая
движущейся материальной точкой (или
телом) относительно выбранной системы
отсчета называется траекторией.
Уравнение траектории можно получить,
исключив параметр t из
кинематических уравнений. В зависимости
от формы траектории движение может
быть прямолинейным или криволинейным.

Длиной
пути точки
называется сумма длин всех участков
траектории, пройденных этой точкой за
рассматриваемый промежуток
времени s = s(t) .
Длина пути — скалярная функция
времени.

Вектор
перемещения r
r r0 r
r r = —
вектор, проведенный из начального
положения движущейся точки в положение
ее в данный момент времени (приращение
радиуса-вектора точки за рассматриваемый
промежуток времени).

Линию,
по которой движется материальная точка
в пространстве, называют траекторией
ее движения.
Иными словами, траекторией
движения называют
совокупность всех последовательных
положений, занимаемых материальной
точкой при ее движении в пространстве.

Одним
из основных понятий механики является
понятие материальной точки,
что означает тело, обладающее массой,
размерами которого можно пренебречь
при рассмотрении его движения. Движение
материальной точки — простейшая задача
механики, которая позволит рассмотреть
более сложные типы движений.

Перемещение
материальной точки происходит в
пространстве и изменяется со временем.
Реальное пространство трехмерно, и
положение материальной точки в любой
момент времени полностью определяется
тремя числами — ее координатами в
выбранной системе отсчета. Число
независимых величин, задание которых
необходимо для однозначного определения
положения тела, называется числом его
степеней свободы. В качестве системы
координат выберем прямоугольную, или
декартову, систему координат. Для
описания движения точки, кроме системы
координат, необходимо еще иметь
устройство, с помощью которого можно
измерять различные отрезки времени.
Такое устройство назовем часами.
Выбранная система координат и связанные
с ней часы образуют систему отсчета.

Декартовы
координатыX,Y,Z
определяют
в пространстве радиус-вектор z,
острие которого описывает при его
изменении со временем траекторию
материальной точки. Длина траектории
точки представляет собой величину
пройденного пути S(t).
Путь S(t)—
скалярная величина. Наряду с величиной
пройденного пути, перемещение точки
характеризуется направлением, в котором
она движется. Разность двух радиус-векторов,
взятых в различные моменты времени,
образует вектор перемещения точки
(рис.).

Для
того чтобы характеризовать, как быстро
меняется положение точки в пространстве,
пользуются понятием скорости. Под
средней скоростью движения по траектории
за конечное время t
понимают
отношение пройденного за это время
конечного пути S
ко времени:

. (1.1)

Скорость
движения точки по траектории — скалярная
величина. Наряду с ней можно говорить
о средней скорости перемещения точки.
Эта скорость — величина, направленная
вдоль вектора перемещения,

. (1.2)

Если
моменты времени t₁,
и t₂
бесконечно
близки, то время t
бесконечно
мало и в этом случае обозначается через
dt.
За время dt
точка
проходит бесконечно малое расстояние
dS.
Их отношение образует мгновенную
скорость точки

. (1.3)

Производная
радиус-вектора r
по
времени определяет мгновенную скорость
перемещения точки.

. (1.4)

Поскольку
перемещение совпадает с бесконечно
малым элементом траектории dr
= dS,
то вектор скорости направлен по
касательной к траектории, а его величина:

. (1.5)

На
рис. показана зависимость пройденного
путиS
от
времени t.
Вектор скорости v(t)
направлен по касательной к кривой S(t)
в момент времени t.
Из рис. видно, что угол наклона касательной
к оси t
равен

.

Интегрируя
выражение (1.5) в интервале времени от
t₀
до t,
получим формулу, позволяющую вычислить
путь, пройденный телом за время t—t₀
если
известна зависимость от времени его
скорости v(t)

. (1.6)

Геометрический
смысл этой формулы ясен из рис. По
определению интеграла пройденный путь
представляет собой площадь, ограниченную
кривойv
=v(t)
в интервале от t₀
до t.В
случае равномерного движения, когда
скорость сохраняет свое постоянное
значение во все время движе­ния,
v=const;
отсюда следует выражение

, (1. 7)

где
S₀
‑ путь,
пройденный к начальному времени t₀.

Производную
скорости по времени, которая является
второй производной по времени от
радиус-вектора, называют ускорением
точки:

. (1.8)

Вектор
ускорения а направлен вдоль вектора
приращения скорости dv.
Пусть а = const.
Этот важный и часто встречаемый случай
носит название равноускоренного или
равнозамедленного (в зависимости от
знака величины а) движения. Проинтегрируем
выражение (1.8) в пределах от t
= 0 до t:

(1.9)

(1.10)

и
используем следующие начальные условия:
.

Таким
образом, при равноускоренном движении

. (1.11)

В
частности, при одномерном движении,
например вдоль оси X,
.
Случай прямолинейного движения изображен
на рис. При больших временах зависимость
координаты от времени представляет
собой параболу.

Вобщем случае движение точки может быть
криволинейным.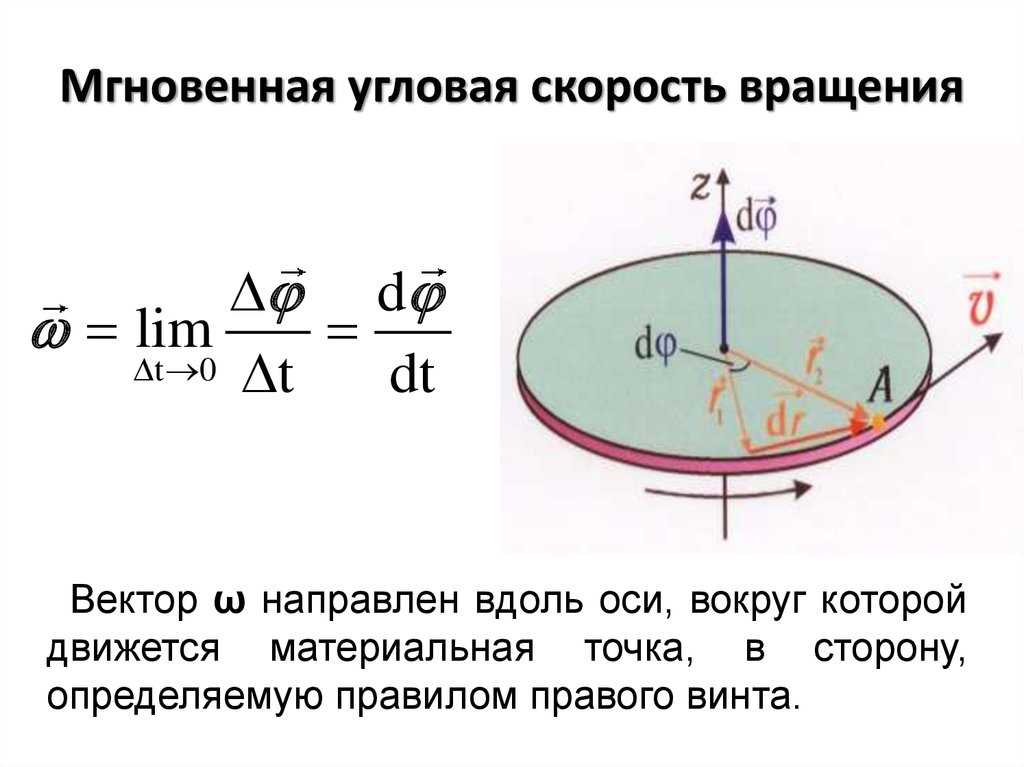 Рассмотрим этот тип
движения. Если траектория точки
произвольная кривая, то скорость и
ускорение точки при ее движении по этой
кривой меняются по величине и направлению.

Выберем
произвольную точку на траектории. Как
всякий вектор, вектор ускорения можно
представить в виде суммы его составляющих
по двум взаимно перпендикулярным осям.
В качестве одной из осей возьмем
направление касательной в рассматриваемой
точке траектории, тогда другой осью
окажется направление нормали к кривой
в этой же точке. Составляющая ускорения,
направленная по касательной к траектории,
носит название тангенциального
ускорения
a_t,
а направленная ей перпендикулярно —
нормального
ускорения
a_n.

Получим
формулы, выражающие величины a_t,
и a_n
через
характеристики движения. Для простоты
рассмотрим вместо произвольной
криволинейной траектории плоскую
кривую. Окончательные формулы остаются
справедливыми и в общем случае неплоской
траектории.

Благодаря
ускорению скорость точки приобретает
за времяdt
малое
изменение dv.
При этом тангенциальное ускорение,
направленное по касательной к траектории,
зависит только от величины скорости,
но не от ее направления. Это изменение
величины скорости равно dv.
Поэтому тангенциальное ускорение может
быть записано как производная по времени
от величины скорости:

. (1.12)

С
другой стороны, изменение dv_n,
направленное перпендикулярно к v,
характеризует только изменение
направления вектора скорости, но не
его величины. На рис. показано изменение
вектора скорости, вызванное действием
нормального ускорения. Как видно из
рис.
,
и, таким образом, с точностью до величины
второго порядка малости величина
скорости остается неизменнойv=v’.

Найдем
величину a_n.
Проще всего это сделать, взяв наиболее
простой случай криволинейного движения
— равномерное движение по окружности.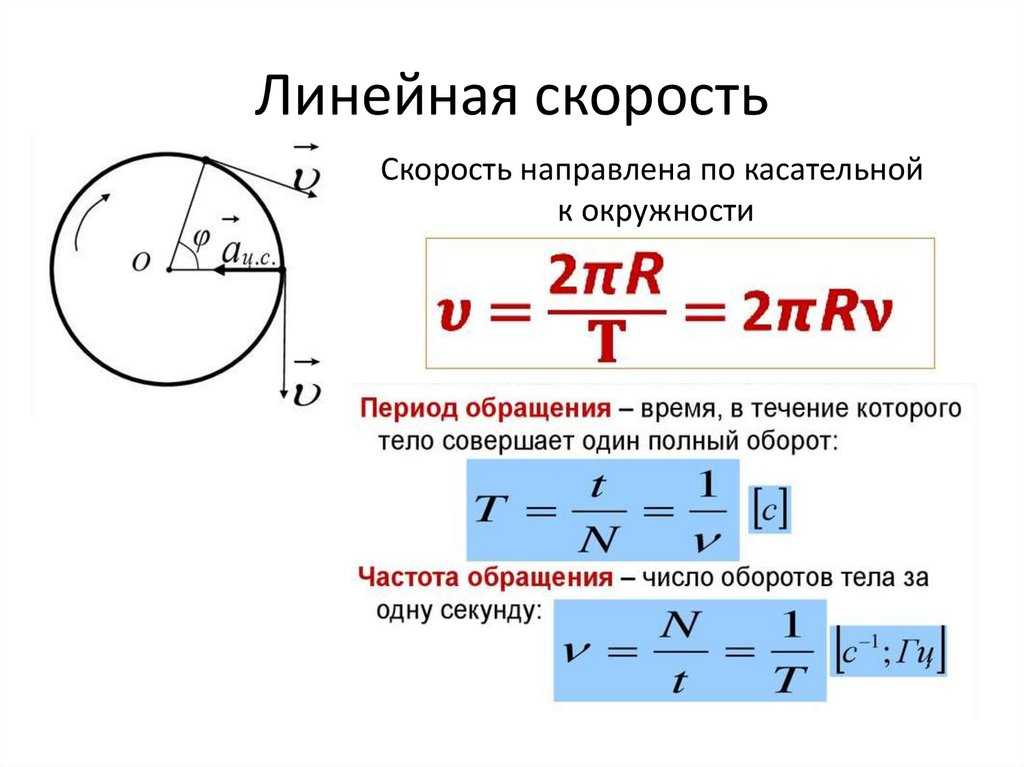
При этом a_t=0.
Рассмотрим перемещение точки за время
dt
по дуге
dS
окружности
радиуса R.

Скоростиv и
v’ ,
как отмечалось, остаются равными по
величине. Изображенные на рис. треугольники
оказываются, таким образом, подобными
(как равнобедренные с равными углами
при вершинах). Из подобия треугольников
следует
,
откуда находим выражение для нормального
ускорения:

. (1.13)

Формула
для полного ускорения при криволинейном
движении имеет вид:

. (1.14)

Подчеркнем,
что соотношения (1.12), (1.13) и (1.14) справедливы
для всякого криволинейного движения,
а не только для движения по окружности.
Это связано с тем, что всякий участок
криволинейной траектории в достаточно
малой окрестности точки можно приближенно
заменить дугой окружности. Радиус этой
окружности, называемый радиусом кривизны
траектории, будет меняться от точки к
точке и требует специального вычисления.
Таким образом, формула (1. 14) остается
справедливой и в общем случае
пространственной кривой.

Движение
твердого тела, при котором две его
точки О и О‘
остаются неподвижными, называется вращательным
движением вокруг
неподвижной оси, а неподвижную прямую ОО‘
называют осью
вращения. 
      
Пусть абсолютно твердое тело вращается
вокруг неподвижной оси ОО‘
(рис. 2.12).

Рис.
2.12

      
Проследим за
некоторой точкой М этого
твердого тела. За время  dt 
точка М совершает
элементарное перемещение  dr. 
      
При том же самом угле поворота  dφ,
другая точка, отстоящая от оси на большее
или меньшее расстояние, совершает
другое перемещение. Следовательно, ни
само перемещение некоторой точки
твердого тела, ни первая производная ,
ни вторая производная  не
могут служить характеристикой движения
всего твердого тела. 
      
За это же время dt радиус-вектор R,
проведенный из точки 0‘
в точку М,
повернется на угол  dφ.
На такой же угол повернется радиус-вектор
любой другой точки (т.к. тело абсолютно
твердое, в противном случае расстояние
между точками должно измениться). 
      
Угол поворота  dφ 
характеризует перемещение всего тела
за время dt. 
      
Удобно ввести  –
вектор элементарного поворота тела,
численно равный  dφ 
и направленный вдоль оси вращения ОО‘
так, чтобы, глядя вдоль вектора, мы
видели вращение по часовой стрелке
(направление вектора  и
направление вращения связаны «правилом
буравчика»). 
      
Элементарные повороты удовлетворяют
обычному правилу сложения векторов:

Угловая
скорость вращения
тела

Угловой
скоростью тела
в данный момент t называется величина,
к которой стремится средняя угловая
скорость ,
если  стремится
к нулю.

Угловая
скорость твердого тела является первой
производной от угла поворота по времени.

Размерность:
[радиан/время]; [1/время]; [1/сек =].

Угловую
скорость можно изображать вектором.
Вектор угловой скорости направляют
по оси вращения в ту сторону, откуда
вращение видно против хода часовой
стрелки.

Если
угловая скорость не является постоянной
величиной, то вводят еще одну характеристику
вращения — угловое ускорение.

Угловое
ускорение характеризует изменение
угловой скорости тела с течением
времени.

Если
за промежуток времени  угловая
скорость получает приращение ,
то среднее угловое ускорение равно

вращение, — один
из простейших видов движения твёрдого
тела. В. д. вокруг неподвижной оси —
движение, при к-ром все точки тела,
двигаясь в параллельных плоскостях,
описывают окружности с центрами,
лежащими на одной неподвижной прямой,
перпендикулярной к плоскостям этих
окружностей и наз. осью вращения.
Скорость произвольной точки тела v =
[w, r], где w — угловая
скорость тела,
г — радиус-вектор, проведённый в точку
из центра описываемой ею окружности.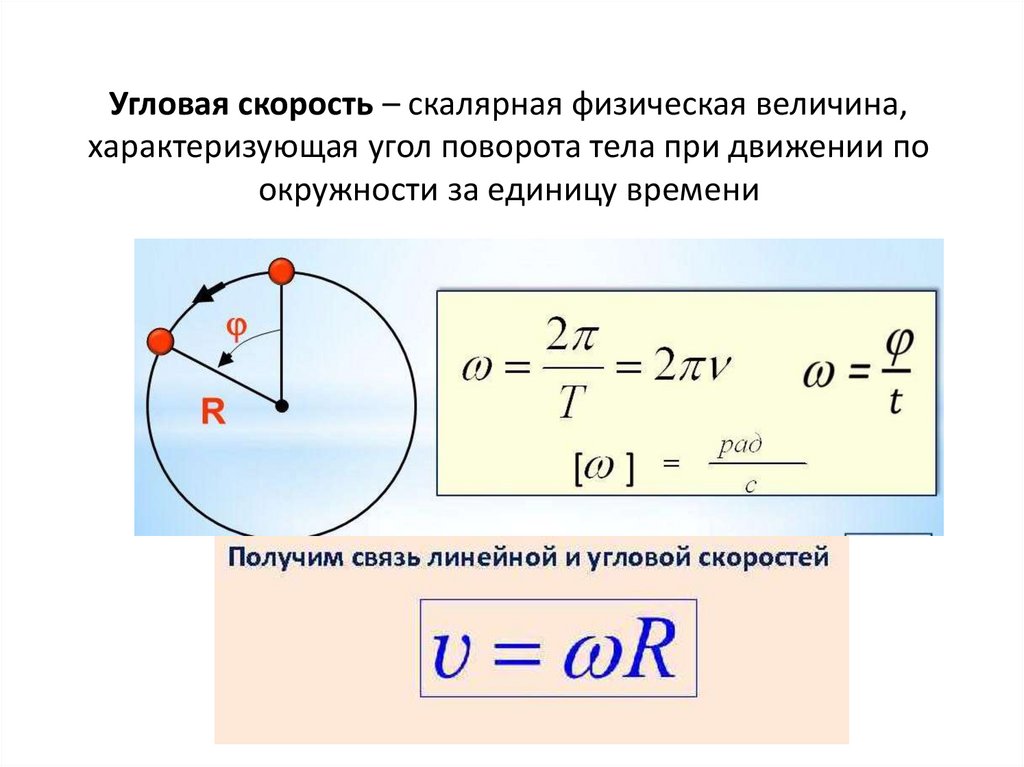 Угловое
ускорение тела
e = М/I, где М — момент внеш. сил относительно
оси вращения, I — момент инерции тела
относительно той же оси.

В. д. вокруг
неподвижной точки — движение, при к-ром
все точки тела движутся по поверхностям
концентрич. сфер с центрами в неподвижной
точке. В каждый момент времени это
движение можно рассматривать как
вращение вокруг мгновенной оси вращения,
проходящей через неподвижную точку.
Скорость произвольной точки тела v =
[to, г], здесь г — радиус-вектор, проведённый
в точку из неподвижной точки тела.
Основной закон динамики: dL/dt
= М,
где L — момент
импульса тела
относительно неподвижной точки, М —
момент относительно той же точки всех
внеш. сил, приложенных к телу, наз.
главным моментом внешних сил. Этот
закон справедлив также для вращения
твёрдого тела вокруг его центра инерции
независимо от того, покоится последний
или движется произвольно. Теория В. д.
имеет многочисл. приложения в небесной
механике, внеш. баллистике, теории
гироскопа, теории машин и механизмов.

Пройденный
путь S
, перемещение
dr,
скорость v
, тангенциальное
и нормальное ускорение a_t,
и a_n,
представляют собой линейные величины.
Для описания криволинейного движения
наряду с
ними
можно
пользоваться угловыми величинами.

Рассмотрим
более подробно важный и часто встречаемый
случай движения по окружности. В этом
случае наряду с длиной дуги окружности
движение можно характеризовать утлом
поворота φ
вокруг оси вращения. Величину

(1.15)

называют
угловой скоростью.
Угловая скорость представляет собой
вектор, направление которого связывают
с направлением оси вращения тела (рис.).

Обратим
внимание на то, что, в то время как сам
угол поворота φ
является скаляром, бесконечно малый
поворот dφ
— векторная
величина, направление которой определяется
по правилу правой руки, или буравчика,
и связано с осью вращения.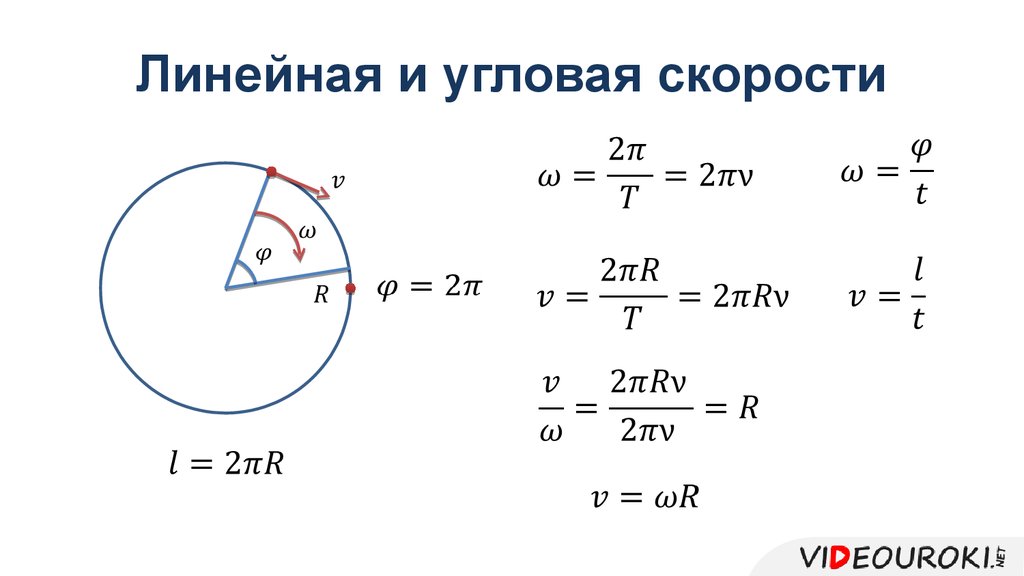 Если вращение
является равномерным, то ω=const
и точка на
окружности поворачивается на равные
углы вокруг оси вращения за равные
времена. Время, за которое она совершает
полный оборот, т.е. поворачивается на
угол 2π,
называется
периодом движения
Т.
Выражение (1.15) можно проинтегрировать
в пределах от нуля до Т
и получить
угловую частоту

. (1.16)

Число
оборотов в единицу времени есть величина,
обратная периоду, — циклическая частота
вращения

ν
=1/T. (1.17)

Нетрудно
получить связь между угловой и линейной
скоростью точки. При движении по
окружности элемент дуги связан с
бесконечно малым поворотом соотношением
dS = R·dφ.
Подставив его в (1.15), находим

v
= ωr. (1.18)

Формула
(1.18) связывает величины угловой и
линейной скоростей. Соотношение,
связывающее векторы ω
и v,
следует из рис. А именно, вектор линейной
скорости представляет собой векторное
произведение вектора угловой скорости
и радиуса-вектора точки r:

. (1.19)

Таким
образом, вектор угловой скорости
направлен по оси вращения точки и
определяется по правилу правой руки
или буравчика.

Угловое
ускорение
— производная по времени от вектора
угловой скорости ω (соответственно
вторая производная по времени от угла
поворота)

Выразим
тангенциальное и нормальное ускорение
через угловые скорости и ускорение.
Используя связь (1.18),(1.12) и (1.13), получаем

a_t
= β·R,
a
=ω²·R. (1.20)

Таким
образом, для полного ускорения имеем

. (1.21)

Величина
β
играет роль тангенциального ускорения:
если β =
0.полное ускорение при вращении точки
не равно нулю, a
=R·ω²
≠ 0.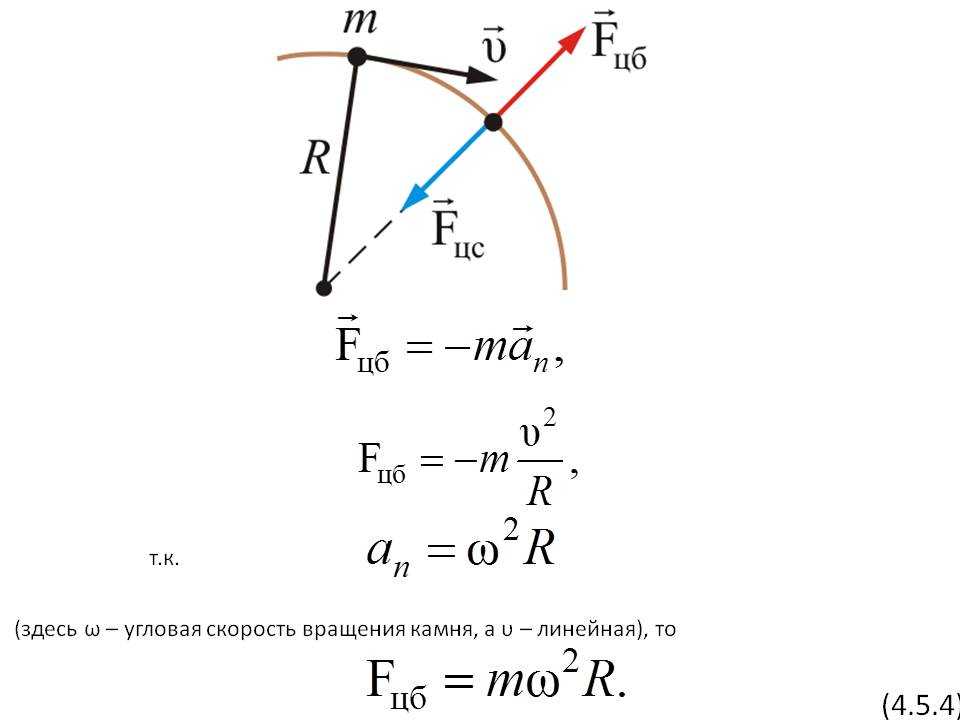

3. Динамика
поступательного движения. Законы
Ньютона. (Савельев И.В. Т.1 § 7, 9, 11).
Основные физические величины и их
размерности. (Савельев И.В. Т.1 § 10).
Виды сил в механике. (Савельев И.В. Т.1
§ 13–16).

об/мин против угловой скорости |

••• Photos.com/AbleStock.com/Getty Images

Обновлено 25 апреля 2017 г. точка, используются для решения задач физики, машиностроения и компьютерного программирования. Часто число оборотов в минуту и ​​угловая скорость используются взаимозаменяемо для имитации вращения шкивов и качения колес в инженерных симуляторах и видеоиграх.

Угловая скорость Использование

Угловая скорость используется для выражения скорости вращения круглого объекта, например колеса. Поскольку в окружности 360 градусов, колесо, совершающее один полный оборот вокруг своего центра за одну секунду, будет иметь угловую скорость 360 градусов в секунду. Поскольку секундной стрелке часов требуется 60 секунд, чтобы сделать один полный оборот вокруг своего центра, ее угловая скорость составляет 360 градусов каждые 60 секунд или 6 градусов в секунду.

оборотов в минуту Использование

Число оборотов в минуту также используется для выражения скорости вращения круглого объекта, например колеса. Поскольку один оборот эквивалентен одному полному обороту или вращению вокруг центральной точки, говорят, что колесо, совершающее один полный оборот вокруг своего центра за минуту, вращается вокруг своего центра со скоростью 1 оборот в минуту или 1 об/мин. Поскольку секундной стрелке часов требуется 1 минута, чтобы сделать один полный оборот вокруг своего центра, ее скорость вращения составляет 1 оборот в минуту или 1 об/мин.

Преобразование угловой скорости в число оборотов в минуту

Угловую скорость в градусах в секунду можно преобразовать в обороты в минуту, умножив угловую скорость на 1/6, поскольку один оборот равен 360 градусам, а в минуте 60 секунд. Если угловая скорость задана как 6 градусов в секунду, об/мин будет равна 1 обороту в минуту, поскольку 1/6, умноженное на 6, равно 1.

Преобразование угловой скорости в обороты в минуту градусов в секунду, умножив число оборотов на 6, так как один оборот равен 360 градусам, а в минуте 60 секунд. Если скорость вращения равна 1 об/мин, то угловая скорость в градусах в секунду будет равна 6 градусам в секунду, поскольку 6, умноженное на 1, равно 6,9.0003

Связанные статьи

Ссылки

• Центральный Мичиганский университет, факультет физики; Физика для спортсменов; Глава 6: Угловое движение
• ComputerHope: об/мин
• SparkNotes: SAT Physics — частота и период

Об авторе

Марк Стансберри 15 лет работает техническим и бизнес-писателем. Его работы были опубликованы в ведущих технических и деловых изданиях, таких как Red Herring, EDN и BCC Research. В настоящее время он занимается программированием компьютерных приложений, автоматизацией графического дизайна, трехмерной линейной перспективой и фрактальными технологиями. Стэнсберри имеет степень бакалавра электротехники Университета штата Сан-Хосе.

Фото кредиты

Photos.com/AbleStock.com/Getty Images

3 Краткие факты – Lambda Geeks

 Вы уже знали, что такое скорость и скорость. Но понятия угловой скорости и скорости — это физические величины, которые необходимо понимать.

Когда объект должен двигаться по круговой траектории под определенным углом, это называется угловым движением. Понятие угловой скорости и угловой скорости — это величины, полученные из углового движения объекта. Изучим эти понятия подробно.

Угловая скорость против угловой скорости

Прежде чем перейти к обсуждению сравнения между угловой скоростью и угловой скоростью, давайте изучим значение угловой скорости и угловой скорости и формулу, которая используется для расчета.

Угловые движения.

Что такое угловая скорость?

Предположим, что вы вращаете мяч по круговой орбите, тогда угловая скорость может быть определена, как показано ниже.

Угловая скорость – это мера того, насколько быстро тело меняет свой угол со временем при вращении по круговой орбите.

Формула для расчета угловой скорости.

Чтобы измерить угловую скорость вращающегося объекта, мы должны вычислить число оборотов, которые тело совершает за единицу времени. Угол поворота следует брать в радианах.

Для прямого угла мы определяем радиан как π/2, который совершается при движении, поэтому для полного поворота он составляет 2π радиан.

Угловая скорость обозначается символом ω; это дается уравнением,

Где; θ — угол поворота, t — время, затрачиваемое на один оборот.

Что такое угловая скорость?

Когда объект вращается по круговой орбите с некоторой скоростью, угловая скорость может быть определена так же, как линейная скорость.

Скорость изменения расстояния, пройденного телом по равномерному круговому пути, за время, затрачиваемое телом на перемещение, называется угловой скоростью.

F Формула для расчета угловой скорости.

Чтобы вычислить угловую скорость, мы должны знать направление, в котором вращается тело.

Предположим, что объект вращается против часовой стрелки; тогда угловая скорость определяется как;

Где; dθ — изменение углового смещения

dt — изменение во времени.

Сравнение между угловой скоростью и угловой скоростью:

Зная разницу между угловой скоростью и угловой скоростью, можно легко понять концепцию .

Угловая скорость	Угловая скорость
Угловая скорость — это скалярная мера вращающегося объекта.	Угловая скорость — это векторная мера вращающегося объекта.
Угловая скорость определяет только величину.	Угловая скорость определяет как величину, так и направление.
Единицей измерения угловой скорости является радиан в секунду.	Единицей измерения угловой скорости также является радиан в секунду.
У него нет правильного направления вращения.	Вращается в определенном направлении вдоль осей, либо по часовой стрелке, либо против часовой стрелки.
Скорость изменяется по круговой траектории при изменении угла.	Скорость остается постоянной, хотя углы продолжают изменяться.
Угловая скорость дает абсолютное значение вектора скорости, поэтому оно должно быть положительным или нулевым.	Угловая скорость может стать отрицательной всякий раз, когда он вращается вокруг отрицательной оси.

Угловая скорость по круговой траектории.

Рассмотрим тело, вращающееся по однородной круговой орбите радиусом «r». Тело перемещается из одного положения в другое, образуя угол θ за время t.

Угловая скорость определяется выражением;

Скорость, с которой тело перемещается из одного положения в другое, определяется как

с — это перемещение, которое представляет собой не что иное, как длину дуги окружности; определяется выражением

s= r|∆θ|

Теперь, подставив значения

Но

 Что является величиной угловой скорости

Скорость = |ω| r

Приведенное выше уравнение подразумевает, что угловая скорость представляет собой величину угловой скорости и радиус пути, по которому движется объект.

Некоторые решенные проблемы.

Шарик вращается по круговой траектории с определенной скоростью. I т вращается π радиан за каждые 6 секунд. C вычислить скорость вращения.

Решение:

       Скорость задана

Скорость вращения равна 1/6 , скорость задана как

, т.е. ω = 6π рад/сек.

Шина вращается по круговой орбите радиусом 12 см. Угол поворота составляет 9 радиан за каждые 3 секунды. Узнать угловую скорость?

Решение:

Угловая скорость определяется выражением;

Полный оборот шины составляет 360°. Следовательно, оборот составляет 2π радиан.

ω = 6π рад/сек.

Диск диаметром 25 м вращается со скоростью 16 м/с. Вычислите угловую скорость шины.

Решение:

        Дано:  Диаметр шины = 25 м.

Вычислите скорость Земли, которая обращается вокруг Солнца за 365 дней.

Решение:

Земля занимает 365 дней = T = 365 × 24 × 60 × 609

T = 31536000 с.

Поскольку Земля вращается по круговой орбите, для одного полного оборота требуется 2π радиан.

Угловая скорость равна

ω = 1,99 × 10 ^-4 единиц/сек.

F Часто задаваемые вопросы.

Что подразумевается под псевдовектором?

Когда физическая величина имеет как величину, так и направление, говорят, что эта величина является Вектором.

A Псевдо-векторы также имеют как величину, так и направление. Но он меняет свою ориентацию при изменении координатных осей.

Как зависит угловая скорость от направления?

Угловая скорость действует в направлении оси вращения.

Если скорость направлена ​​к оси вращения, объект вращается против часовой стрелки. Если скорость действует против оси вращения, объект подвергается вращению по часовой стрелке.

Как угловая скорость остается постоянной при круговом движении?

Скорость тела остается неизменной даже при изменении направления.

Когда тело совершает круговое движение, его направление может постоянно меняться. Поскольку это векторная величина, величина уравновешивает изменение положения, а угловая скорость остается постоянной.      

Как центростремительная сила влияет на угловую скорость?

Центростремительная сила действует перпендикулярно скорости вдоль круговой траектории.

Сила трения вносит вклад в центростремительную силу, которая равна угловой скорости. Чем больше центростремительная сила, тем меньше будет радиус, но скорость останется прежней.

Изменяет ли радиус угловую скорость тела?

Радиус не вызывает никаких изменений угловой скорости.