Содержание
3.4.4. Определение окружной скорости несущего винта
Величина
окружной скорости
(
‒
угловая скорость) несущего винта (НВ)
существенно влияет на ЛТХ вертолета.
Как и для
самолета,
вертолета в горизонтальном полете
ограничена
располагаемой мощностью
силовой установки. Однако для вертолета
максимальная скорость полета
ограничивается также
влиянием
сжимаемости воздуха на наступающей и
срывом потока
на отступающей лопастях.
Окружную
скорость концов НВ у современных
вертолетов
выбирают из условия, чтобы
несущий винт на режиме висения имел
достаточно высокий КПД 0
(0 = 0,72…0,77),
а на максимальной скорости полета не
было бы срыва потока на отступающей
(идущей
с набегающим потоком) лопасти и явлений
сжимаемости на наступающей, идущей
против потока, лопасти.
Окружная
скорость концов НВ у современных легких
вертолетов принимается равной
= 180…205 м/с [28, 36, 93]. Представляют
Представляют
практический интерес НВ легких вертолетов
с
= 210…215 м/с.
Следует
учитывать [28], что:
– двигатели
силовых установок вертолетов не
обеспечивают необходимой мощности при
изменении оборотов в широких пределах;
– современные
трансмиссии не дают переменной редукции;
– силу
тяги НВ целесообразно повышать посредством
увеличения шага 0
НВ при уменьшении числа его оборотов
до их минимально допустимой величины.
Минимально
допустимая частота вращения НВ в полете
на всех режимах ограничивается
обеспечением:
– запаса
по срыву потока с лопасти при полете на
скорости
;
– запаса
путевого управления на взлетно-посадочных
режимах
и продольно-поперечного
управления при полете по маршруту;
– прочности
главного редуктора по крутящему моменту
НВ;
– запаса
кинетической энергии вращения НВ для
возможного перехода на режим самовращения;
– функционирования
генераторов переменного тока и всей
системы электроснабжения вертолета.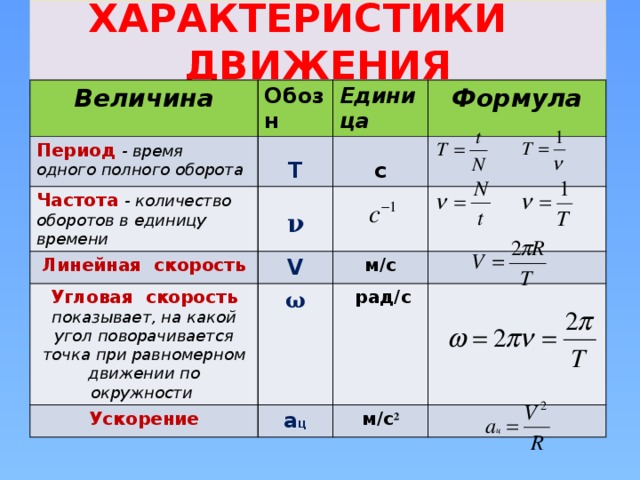
Максимально
допустимая частота вращения НВ в полете
на всех режимах ограничивается условиями:
– обеспечения
прочности главного редуктора, втулки
НВ, автомата перекоса и лопастей по
центробежным силам;
– предотвращения
волнового кризиса на конце наступающих
лопастей НВ при полете вертолета на
больших высотах и скоростях;
– обеспечения
достаточного запаса по флаттеру лопастей
НВ;
– предотвращения
резкого возрастания уровня вибраций и
переменных напряжений в лопастях НВ в
связи с нестационарностью
характера
развития волнового кризиса;
– предотвращения
возникновения (усиления) тряски вертолета;
– исключения
срабатывания защиты свободной турбины
от
раскрутки, т.е. самопроизвольного
выключения двигателей в полете;
– начала
резкого увеличения мощности, потребной
для вращения несущего винта.
Мерой
оценки влияния срыва потока на НВ
является величина СТ /
‑ отношение коэффициента силы
тяги НВ к коэффициенту заполнения,
которое определяет средний по диску
винта коэффициент
подъемной силы
лопасти
.
Для прямоугольной в плане лопасти
.
(3.11)
Предельная
величина СТ /
на азимуте
= 270º,
определяемая по срыву потока при полете
вертолета вперед, зависит от характеристики
режима работы несущего винта μ
(рис. 3.4) [ 28 ]:
, (3.12)
где
‒ угол атаки плоскости диска НВ (
– положительный при наклоне диска НВ
вперед). В горизонтальном полете, когда
мал:
. (3.12а)
Увеличение
,
усиливая неравномерность углов атаки
по диску НВ, приводит к срыву потока на
отступающей лопасти и уменьшению
величины СТ /.
Срыв потока сопровождается нарастанием
вибраций и нагрузок на винт и систему
управления в результате больших
переменных
составляющих шарнирных моментов
лопастей, периодически попадающих в
срыв.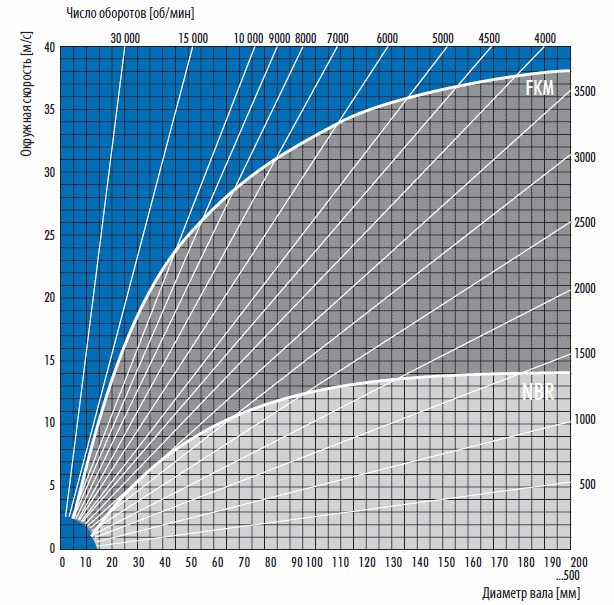 Поэтому срыв потока на отступающей
Поэтому срыв потока на отступающей
лопасти часто является главным фактором,
ограничивающим
.
Рис. 3.4. Зависимость от (или ) |
Мерой
оценки влияния сжимаемости потока на
характеристики НВ служит число
для профиля на конце наступающей лопасти
при азимуте = 90º:
, (3.13)
где
— скорость звука в воздухе.
Влияние
сжимаемости на характеристики вертолета
количественно можно определить по
данным работ [28, 34, 36, 60, 93].
Для
скоростного профиля при
увеличение потребной мощности составляет
15…18%; при
‑ 30%.
‑
критическое значение, при достижении
которого местная скорость обтекания
хотя бы в одной точке на поверхности
профиля становится равной скорости
звука,
=
0,78…0,82 ‒ для типовых профилей
лопасти НВ.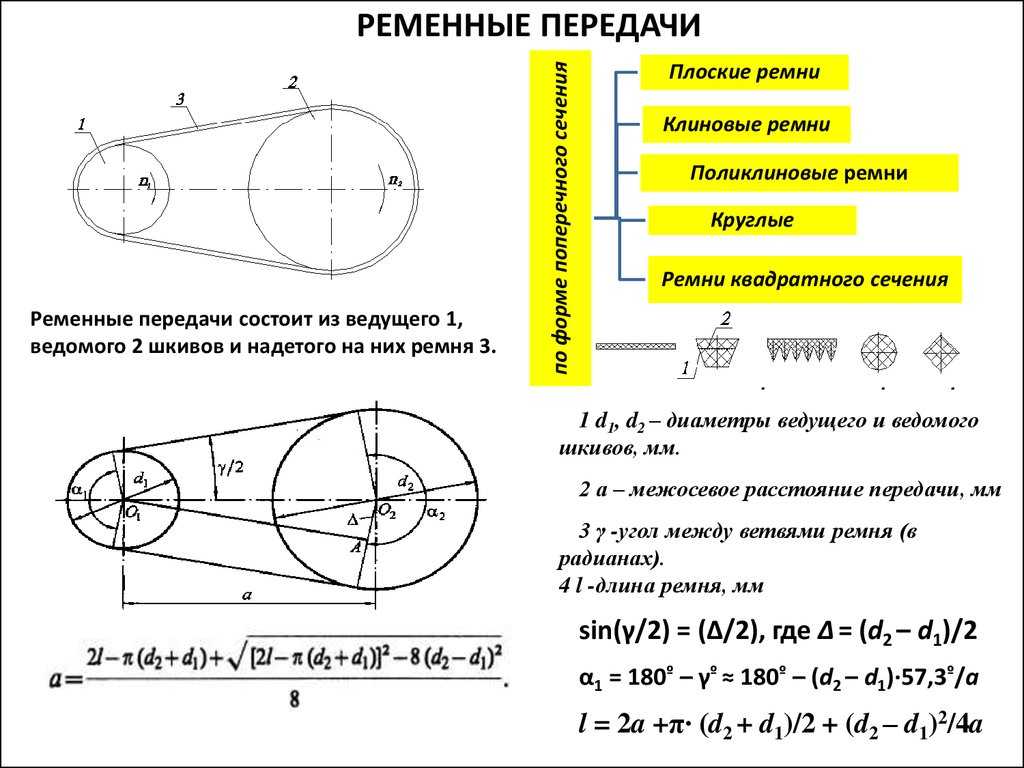 На современных скоростных
На современных скоростных
вертолетах величина
<
0,92…0,95 (исключение составляет
вертолет Westland G-Lynx, у которого
= 0,97). При
влияние сжимаемости потока воздуха
незначительно.
Для
уменьшения вредного влияния сжимаемости
при полете на
в концевых сечениях лопастей применяют
симметричные профили малой относительной
толщины (
= 6…8%),
а также специальные законцовки лопастей
НВ (см. рис. 3.3).
Следует
помнить, что большее значение числа
оборотов НВ
ограничено сжимаемостью
воздуха на азимуте
= 90º,
а малое – срывом потока на азимуте
= 270º.
Решая
уравнения
(3.12) и (3.13) относительно
и
,
получим
; (3.14)
. (3.15)
Используя
выражения (3.14) и (3.15), при заданном
и выбираемом профиле можно найти
и μ, а также построить диаграмму
,
а по ней определить
и μ (рис.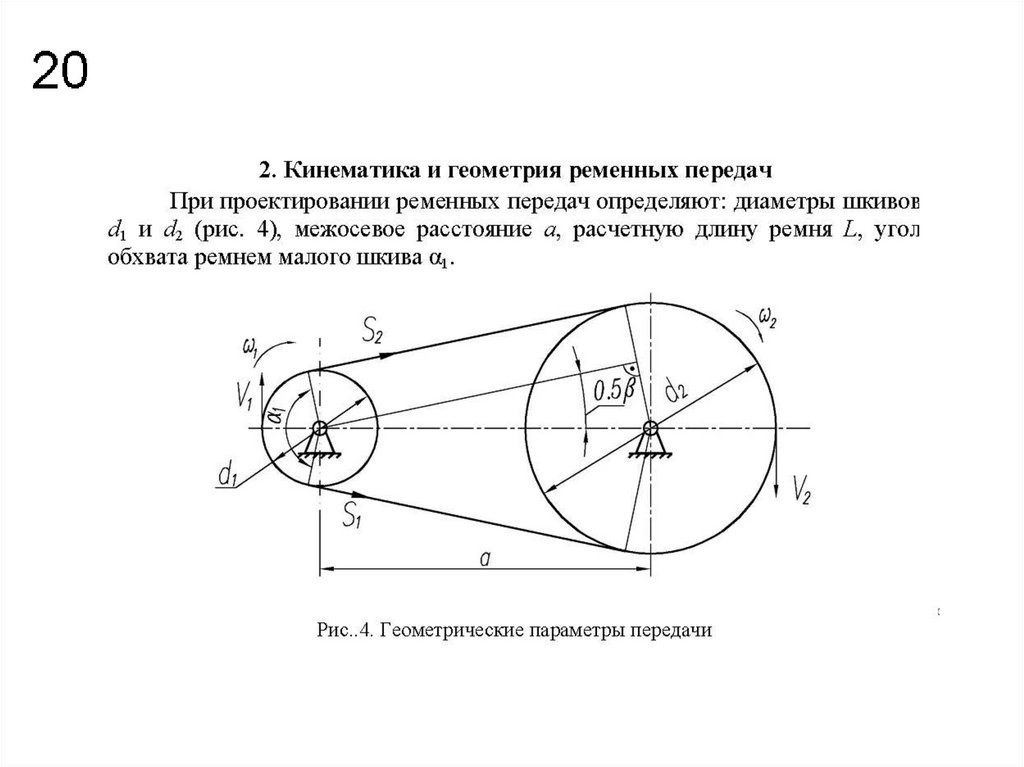 3.5).
3.5).
Ограничение
по
сжимаемости
Ограничение
по
срыву
Рис. 3.5. Диаграмма
зависимости
от V при
и
(= const)
Приведенные рекомендации
и статистические данные позволяют
обоснованно определить окружную скорость
НВ. Например, для
= 0,85
и
= 250 км/ч
получим
= 214 м/с
и μ = 0,32.
Для каждого значения
окружной скорости конца лопасти
существует
наивыгоднейшее заполнение НВ, при
котором значение относительного
(вентиляторного) коэффициента полезного
действия винта на режиме висения
вертолета (в отсутствие ограничивающих
поверхностей) максимально [63].
По
выбранной величине ωR определяют частоту
вращения НВ:
.
(3.16)
когда, почему и подробные факты?
Эта статья отвечает на вопрос, когда угловая скорость постоянна? Скорость изменения смещения называется скоростью.
Простыми словами, это скорость объекта с направлением. Скорость связана с линейным движением, каждая молекула на объекте движется с одинаковой скоростью. Угловая скорость относится к движению, при котором объект вращается вокруг своей оси.
Скорость связана с линейным движением, каждая молекула на объекте движется с одинаковой скоростью. Угловая скорость относится к движению, при котором объект вращается вокруг своей оси.
Что такое угловая скорость?
Скорость векторного вращения любого объекта вокруг своей оси называется угловым скорость. Проще говоря, это измерение того, насколько быстро изменяется угловое положение объекта.
Из приведенного выше обсуждения мы можем сделать вывод, что угловая скорость является сопряженной скоростью для углового движения. Угловая скорость относится к угловому движению так же, как скорость к линейному движению. Мы изучим больше об угловой скорости в разделах ниже.Изображение: угловое движение
Изображение Кредиты: DNET на основе растровой версии, выпущенной под GFDL, Угловая скорость, CC BY-SA 3.0
Формула угловой скорости
Как обсуждалось выше, угловое положение объекта изменяется со временем при угловом движении.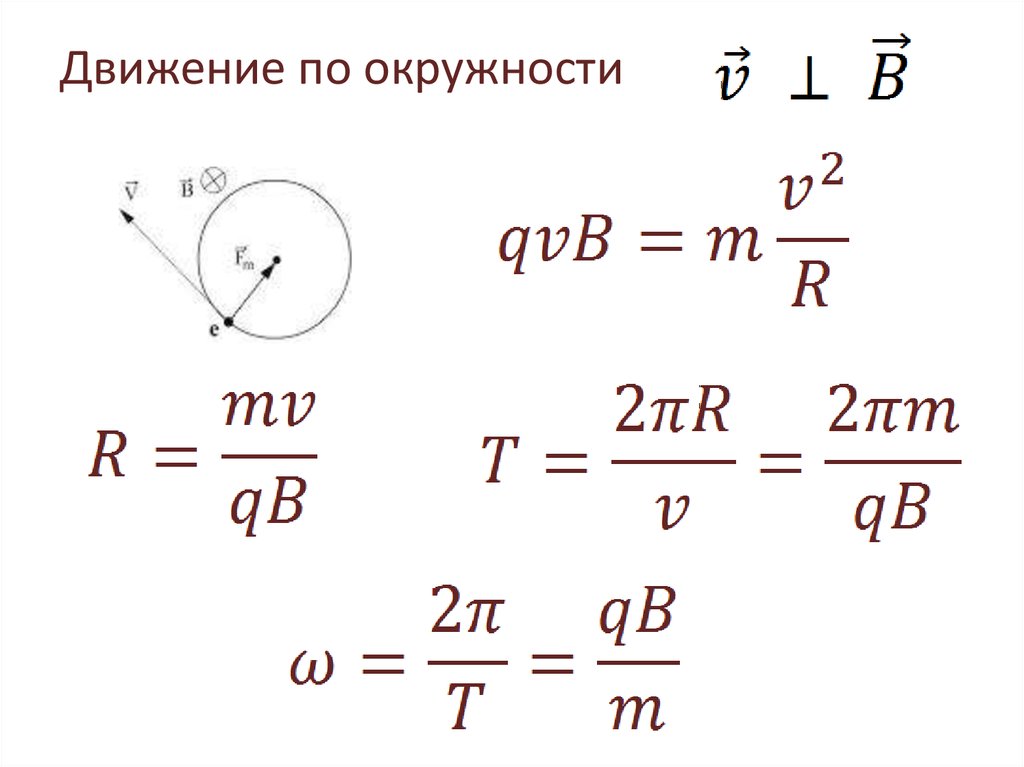 Скорость, с которой она изменяется, называется угловой скоростью. Это может быть дано в терминах угловых терминов, а также может быть получено из терминов, используемых также в линейном движении.
Скорость, с которой она изменяется, называется угловой скоростью. Это может быть дано в терминах угловых терминов, а также может быть получено из терминов, используемых также в линейном движении.
Угловую скорость можно найти, используя линейную скорость, если известен радиус движения. Давайте посмотрим на различные формулы углового движения ниже.
Что касается условий линейного движения- V=rω
где,
r — радиус угловой траектории, по которой движется объект.
V — линейная скорость объекта, перпендикулярного круговой траектории.
ω — угловая скорость объекта
По отношению к угловому движению- ω = dθ/dt
где,
тета — угловое смещение объекта
омега — угловая скорость объекта
dt — рассматриваемое мгновенное время
Когда угловая скорость постоянна?
Когда объект движется по кругу с одинаковой скоростью, можно сделать вывод, что он имеет постоянную угловую скорость.
Таким образом, мы можем сказать, что угловая скорость объекта постоянна, когда он движется с той же скоростью в угловом движении. Вращение Земли является примером постоянного углового движения. Чтобы совершить полный оборот вокруг Солнца, требуется 365 дней.
Почему угловая скорость постоянна?
Причина того, что угловая скорость постоянна, заключается в том, что объект, движущийся по окружности, все время совершает одинаковое угловое смещение.
Это происходит, когда объект имеет одинаковую скорость на всем протяжении углового движения. Имеются равные проекции перемещений тела при его движении с постоянной угловой скоростью.
Пример угловой скорости
Угловая скорость определяется для объектов в угловом движении. Мы можем видеть угловое движение вокруг нас повсюду. Наблюдать за угловыми движениями объектов — обычное дело.
Угловые движения важны для нашего выживания. Рассмотрим несколько примеров углового движения.
- Веселого круга- Карусель — это аттракцион, в котором дети сидят по окружности аттракциона, при включении аттракциона он начинает вращаться вокруг своего центра. Дети также начинают вращаться вокруг центра вращения.
- Революция Земли– Земля обращается вокруг Солнца с периодом времени 365 дней. Это пример углового движения Земли вокруг Солнца.
- Вращение Земли– Земля вращается вокруг своей оси (также называемое вращением оси). Можно сказать, что поверхность Земли находится в угловом движении.
- Игрушечный топ– Игрушечный волчок вращается вокруг своего центра вращения. Это следует за угловым движением.
- Потолочный вентилятор– Лопасти потолочного вентилятора совершают угловое движение, когда вентилятор включен.
- Балерина— Балерина вращается с пальцами ног в качестве центра вращения. Скорость вращения меняется по мере того, как она раздвигает и сужает движения рук.

- Камень, перевязанный ниткой – это самый распространенный пример углового движения. Камень испытывает угловое движение, когда он привязан к нити и вращается.
- Автомобиль или велосипед, движущийся по круговой дорожке– Транспортные средства испытывают угловое движение при движении по круговой или криволинейной траектории.
- Колеса автомобилей– Колеса автомобилей совершают угловое движение. Это движение преобразуется в прямолинейное движение автомобиля.
- Гигантское колесо– Гигантское колесо вращается в угловом движении. Кабины расположены по окружности колеса. Эти кабины следуют угловому движению вместе с колесом.
Типы угловой скорости
Угловые скорости в целом подразделяются на два типа. Мы обсудим эти типы с некоторыми примерами из повседневной жизни в разделе, данном ниже.
Типы угловой скорости:
- Орбитальная угловая скорость– Этот тип скорости существует в объекте, когда объекты в целом вращаются вокруг общего центра вращения.
 Пример, который лучше всего объясняет это, — это Земля, вращающаяся вокруг Солнца. Земля в целом совершает круговое движение вокруг Солнца.
Пример, который лучше всего объясняет это, — это Земля, вращающаяся вокруг Солнца. Земля в целом совершает круговое движение вокруг Солнца. - Угловая скорость вращения— Этот тип угловой скорости существует для объекта, который вращается или вращается вокруг своего центра. Все частицы или молекулы объекта вращаются с центром объекта в качестве центра вращения. Лучшим примером для объяснения угловой скорости вращения является вращение Земли вокруг своей оси вращения. Поверхность Земли (включая землю, реку и земную кору) вращается вокруг центра Земли.
Пример постоянной угловой скорости
В предыдущих разделах мы обсуждали общие примеры угловой скорости. В этом разделе мы обсудим примеры постоянной угловой скорости.
постоянная угловая скорость примеры приведены ниже-
- Обращение Земли вокруг Солнца- Поскольку Земля совершает один оборот за одно и то же время, можно сказать, что она движется с постоянной угловой скоростью.

- Вращение Земли вокруг своей оси вращения— Земле требуется 24 часа, чтобы совершить один оборот, хотя это число немного уменьшается, но изменение очень незначительно. Можно сказать, что оно следует движению с постоянной угловой скоростью.
- Вентилятор на той же скорости- Когда регулятор вентилятора не трогается и вентилятор вращается с одинаковой скоростью, можно сказать, что вентилятор вращается с постоянной угловой скоростью.
- Обращение Луны вокруг Земли- Луне требуется равное количество времени, чтобы совершить один оборот вокруг Земли, можно сказать, что она движется с постоянной угловой скоростью.
- Колеса автомобиля, движущегося с постоянной скоростью– Когда транспортное средство движется с постоянной скоростью, очевидно, что колеса также вращаются с постоянной скоростью или с постоянной угловой скоростью.
Угловая скорость не изменится, если сопротивление угловому движению мало или отсутствует. Без какого-либо сопротивления объекты могут легко достигать движения с угловой скоростью.
Без какого-либо сопротивления объекты могут легко достигать движения с угловой скоростью.
Что происходит с ускорением, когда угловая скорость постоянна?
Скорость изменения угловая скорость тела называется угловым ускорением. Как и когда величина изменяется угловая скорость, величина углового ускорения тоже меняется.
Таким образом, мы можем сказать, что угловое ускорение изменится только при изменении угловой скорости. Если угловая скорость не изменится, то угловое ускорение будет равно нулю.
Преобразование углового движения в линейное движение
Преобразование одного типа движения в другой — очень полезный инструмент, который помогает нам выполнять различные задачи. Некоторые общеизвестные примеры, в которых мы можем видеть угловое движение, преобразованное в линейное, перечислены ниже:
- Автомобили– Круговое движение колес переводится в линейную скорость автомобиля.
- Стойка и шестерня– Движение реечной передачи является примером взаимного преобразования линейное движение к угловому движению.

- Кидать молот– Пока спортсмен вращает молоток, молоток следует угловому движению. Когда спортсмен отпускает молоток, молоток начинает двигаться по параболической траектории.
- Баллер в крикете-Руки мяча совершают угловое движение, мяч также копирует это угловое движение. Затем оно преобразуется в линейное движение, когда мяч отпускается.
- Удар по мячу для гольфа– Кончик клюшки для гольфа следует угловому движению. Угловое движение преобразуется в прямолинейное движение, когда мяч следует по параболе после удара.
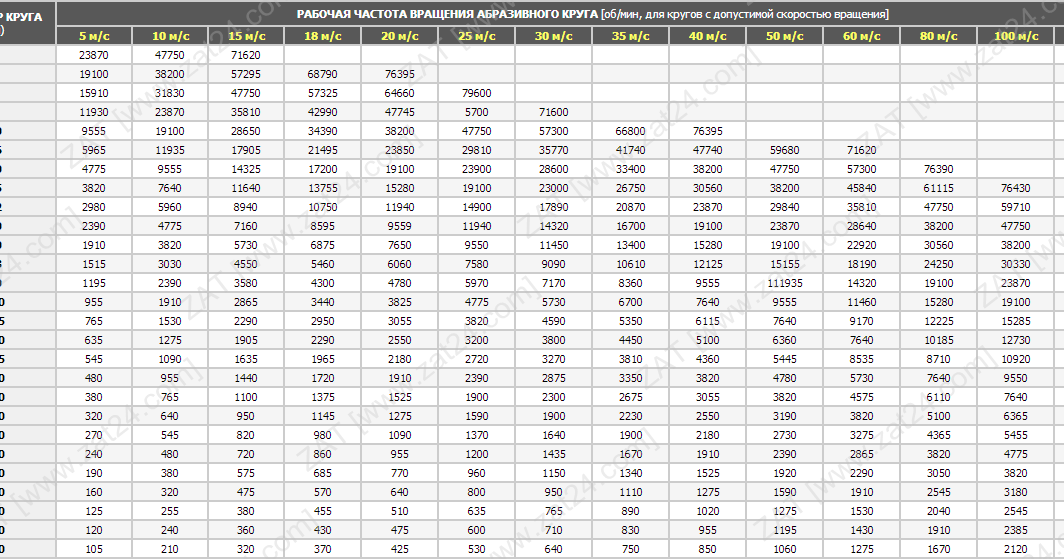
Какова максимальная окружная скорость ремней?
Повышение эффективности машины требует увеличения скорости вращения. Основным критерием для любого используемого типа ремня или цепи является окружная скорость.
Оценки только скорости вращения недостаточно.
Только для скорости вращения всегда следует учитывать диаметр колеса или шкива (которые будут обеспечивать такую производительность).
Окружная скорость рассчитывается по формуле: 9{-1}}]\]
где \(d\) — диаметр вала (колеса или шкива) в м, \(n\) — частота вращения (\(\rm{от. \over s} = \rm{ot. \over min .} \cdot {1 \более 60}\)).
Эта формула показывает, что, например, если у нас есть ручной рубанок со скоростью вращения 10 000 об/мин и шкив малого диаметра 20 мм, результирующая окружная скорость составляет 10,47 м/с. И наоборот, компрессор со скоростью вращения 1500 об/мин и шкивом диаметром 530 мм дает окружную скорость 41,64 м/с!
Необходимо отрегулировать усилие, как указано в таблице, нажав на середину пролета ремня, чтобы проверить силу прогиба ремня. Если прогиб слишком большой, необходимо усилить натяжение ремня; если оно слишком мало, ослабление натяжения ремня уменьшит силу прогиба ремня. Это измерение, однако, является лишь тестом и не дает точного результата. Тем не менее, это намного лучше, чем вообще отсутствие оценочных измерений. См. руководства пользователя устройств и их описания.
Использование ремня в соответствии с максимальной окружной скоростью
- Ремни с оболочкой подходят для скоростей только до 35 м/с.
- Клиновые ремни с необработанными краями и внутренними зубьями XPZ, XPA, XPB, XPC и ZX, AX, BX и CX могут выдерживать скорости до 50 м/с. Существуют приложения, в которых эти ремни могут работать со скоростями более 50 м/с, например. воздуходувки со скоростью 60 м/с. Однако необходимо произвести точные расчеты, провести испытания и обеспечить достаточную балансировку (последнее особенно относится к приводам, использующим ВТП, специальный шкив из высокопрочного чугуна).
- Поликлиновые ремни могут работать с макс. скорость до 60 м/с. Эти ремни могут успешно заменить клиновые ремни в случае высокоскоростных приводов.
- Зубчатые ремни рассчитаны на макс.
 скорость в зависимости от размера профиля, 40-50 м/с. CONTI SYNCHROFORCE CXP и Extreme — это специальные типы, которые могут работать со скоростью до 60 м/с. Для зубчатых ремней при высоких оборотах необходимо следить за уровнем шума. Профили ремня STD или CTD предназначены для самых высоких скоростей.
скорость в зависимости от размера профиля, 40-50 м/с. CONTI SYNCHROFORCE CXP и Extreme — это специальные типы, которые могут работать со скоростью до 60 м/с. Для зубчатых ремней при высоких оборотах необходимо следить за уровнем шума. Профили ремня STD или CTD предназначены для самых высоких скоростей. - Специальные зубчатые ремни CXA предназначены для низкоскоростных трансмиссий. Конструкция и материал этих ремней ограничены окружной скоростью макс. 25 м/с . Эти ремни предназначены для других типов высокоскоростных приводов.
- Плоские ремни могут использоваться в зависимости от типа ремня для макс. скорости 80-100 м/с. Недостатком, однако, является меньшая передаваемая мощность, большая ширина и необходимость большей силы натяжения.
- Для сравнения, цепные приводы могут использоваться в зависимости от размера и типа цепи, для макс.
 скорости около 20 м/с. Важно обеспечить надлежащую смазку и соблюдать все конструктивные требования производителей цепей.
скорости около 20 м/с. Важно обеспечить надлежащую смазку и соблюдать все конструктивные требования производителей цепей.
Балансировка шкивов для высокоскоростных применений
Чем выше окружная скорость, тем выше требования к конструкции шкива, даже ко всему оборудованию. Необходимо отбалансировать шкив с точным классом качества балансировки, т.е. Вопрос 4 – Вопрос 2.5.
Выбор материала и конструкции шкива
Также необходимо выбрать подходящий материал, напр. стали или стального литья, а не чугуна (который не подходит для клиновых и зубчатых ремней при скоростях выше 45 м/с и 35 м/с соответственно). Структура также производит большую центробежную силу; поэтому важно выбрать более прочную конструкцию.
Как уменьшить рабочую окружную скорость привода?
Как показано в формуле, на скорость решающее влияние оказывает окружная скорость и диаметр шкива.
- При использовании клиновых ремней выбирайте новые и современные типы, а не классические.
 Клиновые ремни с внутренними зубьями обладают большей гибкостью, требуют меньше мин. диаметр шкива и способны передавать более высокую мощность. Точно так же приводы могут обойтись меньшим количеством ремней или даже значительно меньшим диаметром шкива.
Клиновые ремни с внутренними зубьями обладают большей гибкостью, требуют меньше мин. диаметр шкива и способны передавать более высокую мощность. Точно так же приводы могут обойтись меньшим количеством ремней или даже значительно меньшим диаметром шкива. - Замените клиновые ремни поликлиновыми ремнями, которые имеют меньший диаметр шкива, большую гибкость и могут передавать более высокие окружные скорости.
- При использовании зубчатых ремней используйте типы с более высокими характеристиками, такие как CXP, которые передают большую мощность и скорость. Тогда становится возможным использовать шкивы меньшего диаметра и уменьшить общий размер привода.
Просмотры
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
Делиться
- Твиттер
- MailTo
Иконка Цитировать
ЦитироватьРазрешения
Поиск по сайту
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- Конечная примечание
- РефВоркс
- Бибтекс
- Процит
- Медларс
| Дж. Турбомаш.
Пропустить пункт назначения навигации
Научная статья
Четан Мистри,
А. М. Прадип
Информация об авторе и статье
Предоставлено Международным институтом газовых турбин (IGTI) ASME для публикации в JOURNAL OF TURBOMACHINERY. Рукопись получена 26 августа 2013 г.; окончательный вариант рукописи получен 15 октября 2013 г.; опубликовано в сети 2 января 2014 г. Доц. Редактор: Аспи Вадиа.
Рукопись получена 26 августа 2013 г.; окончательный вариант рукописи получен 15 октября 2013 г.; опубликовано в сети 2 января 2014 г. Доц. Редактор: Аспи Вадиа.
Дж. Турбомаш . июль 2014 г., 136(7): 071009 (11 страниц)
Номер статьи:
ТУРБО-13-1200
https://doi.org/10.1115/1.4025953
Опубликовано в Интернете: 2 января 2014 г.
История статьи
Получено:
26 августа 2013 г.
Пересмотр получено:
15 октября 2013 г.
Citation
Мистри, К. , и Прадип, А. М. (2 января 2014 г.). «Влияние окружного искажения притока на характеристики низкоскоростного осевого вентилятора с высоким соотношением сторон, вращающегося против направления вращения». КАК Я. Дж. Турбомаш . июль 2014 г.; 136(7): 071009. https://doi.org/10.1115/1.4025953
, и Прадип, А. М. (2 января 2014 г.). «Влияние окружного искажения притока на характеристики низкоскоростного осевого вентилятора с высоким соотношением сторон, вращающегося против направления вращения». КАК Я. Дж. Турбомаш . июль 2014 г.; 136(7): 071009. https://doi.org/10.1115/1.4025953
Скачать файл цитаты:
панель инструментов поиска
Расширенный поиск
В этой статье сообщается о влиянии искажения окружного притока на производительность и поведение потока низкоскоростного вентилятора с большим соотношением сторон и противоположным вращением. Полное давление на входе искусственно искажается с помощью 90-градусного сектора сетки с пористостью 0,70. Рабочие характеристики вентилятора встречного вращения изучались при различных комбинациях скоростей двух роторов в условиях чистого и искаженного притока. Детальный анализ потока был проведен в расчетных и запроектных условиях. Чтобы понять эффект искажения и его степень, сектор искажения вращали по окружности с интервалом 15°, чтобы охватить все кольцевое пространство. Детальные измерения полного давления, составляющих скорости и углов потока проводились на входе в первый ротор, между двумя роторами и на выходе из второго ротора. Исследование выявило несколько интересных аспектов влияния искажения притока на производительность ступени противоположного вращения. Для сочетания расчетной скорости и меньшей частоты вращения ротора-2 наблюдалось сокращение общего рабочего диапазона со смещением точки пикового давления в сторону большего массового расхода. Отмечено, что эффект искривления притока на входе в ротор-1 переносится в сторону вращения ротора-1 и распространяется на все кольцевое пространство.
Рабочие характеристики вентилятора встречного вращения изучались при различных комбинациях скоростей двух роторов в условиях чистого и искаженного притока. Детальный анализ потока был проведен в расчетных и запроектных условиях. Чтобы понять эффект искажения и его степень, сектор искажения вращали по окружности с интервалом 15°, чтобы охватить все кольцевое пространство. Детальные измерения полного давления, составляющих скорости и углов потока проводились на входе в первый ротор, между двумя роторами и на выходе из второго ротора. Исследование выявило несколько интересных аспектов влияния искажения притока на производительность ступени противоположного вращения. Для сочетания расчетной скорости и меньшей частоты вращения ротора-2 наблюдалось сокращение общего рабочего диапазона со смещением точки пикового давления в сторону большего массового расхода. Отмечено, что эффект искривления притока на входе в ротор-1 переносится в сторону вращения ротора-1 и распространяется на все кольцевое пространство. Противоположное направление вращения ротора-2 приводит к тому, что эффект искажения передается в направлении вращения ротора-2 с соответствующим снижением общего давления вблизи ступицы. Замечено, что более высокая скорость вращения второго ротора благотворно влияет на общую производительность из-за сильного всасывания, создаваемого более высокой скоростью вращения ротора-2.
Противоположное направление вращения ротора-2 приводит к тому, что эффект искажения передается в направлении вращения ротора-2 с соответствующим снижением общего давления вблизи ступицы. Замечено, что более высокая скорость вращения второго ротора благотворно влияет на общую производительность из-за сильного всасывания, создаваемого более высокой скоростью вращения ротора-2.
Раздел выпуска:
Исследовательские работы
Темы:
Поток (динамика),
Приток,
Давление,
Роторы,
Дизайн
1.
Bourdon
,
M. W.
,
1942
, «
ROTOR CONTRATING PROPLENGE
»,
Automot. Авиа. инд.
,
86
(
12
), стр.
920–921
.
2.
FAIRHURST
,
L. G.
,
1944
, «
Contra Rotating Aircrews
40097,
.
–
425
.
3.
Watson
,
C. B.
,
1947
, «
Дуплексные авиазонки
»,
Полет
,
L1
, с.
1
—
6
.
4.
Young
,
R. H.
,
1951
, «
Вентилятор вращения
»,
J. Inst. Нагревать. Вентиляционный инж.
Inst. Нагревать. Вентиляционный инж.
,
18
(
187
), стр.
448
–
477
.
5.
Roy
,
B.
,
Kumar
,
H.
и
BATRA
,
A.
,
9000 9000
9999999999999929009
979009
979009
7
7
7
,
A.
,
,
. «
«
Влияние искажений на входе, совместной и встречной закрутки на одноступенчатый осевой вентилятор и осевые вентиляторы, вращающиеся в противоположных направлениях
»,
Труды ISABE
, Бангалор, Индия, 3–7 сентября, документ № ISABE. -2001-1163.
6.
Sharma
,
P. B.
и
Adekoya
,
A.
,
1996
, «
А. Обзор Недавнего исследования. Ступень компрессора
»,
Материалы Международного конгресса и выставки по газовым турбинам и авиационным двигателям
, Бирмингем, Великобритания, 10–13 июня, доклад № 96-GT-254.
7.
Кац
,
R.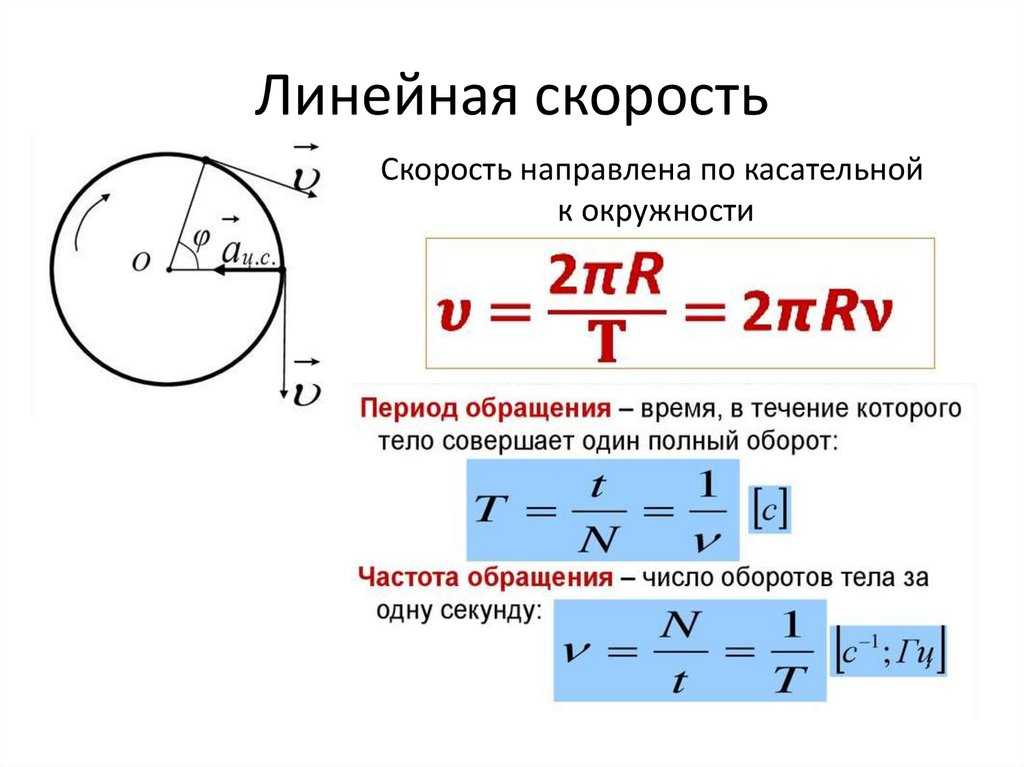
,
1958
, «
Характеристики осевых компрессоров с асимметричными входными потоками
», Управление научных исследований ВВС, отчет № TR-59-8.
8.
Reid
,
C.
,
1969
, «
Отклик компрессоров осевых потоков на искажение потока впуска
», ASME Paper № 69-GR-29.
9.
Пирсон
,
H.
и
McKenzie
,
A.
,
1959
, «
Wakes In Axial Compressors
»,
J………………………………. ………………………………………………………… соц.
………………………………………………………… соц.
,
63
, стр.
415
–
416
.
10.
Cumpsty
,
Нет данных
,
1989
,
Аэродинамика компрессора
,
Лонгманс
,
Лондон
.
11.
Ehrich
,
F.
,
1957
, «
. , с.0003
A. M.
и
Henderson
,
R. J.
,
1980
, «
Влияние некоторых дизайнерских параметров маршрутированного ротора на входном потоке. ASME: J. Eng. Power
ASME: J. Eng. Power
,
102
, pp.
178
–
186
.10.1115/1.3230219
13.
Plourde
,
G. A.
,
1968
, «
Ослабление окружных искажений на входе в многоступенчатых осевых компрессорах
»,
J. Aircr.
,
5
(
3
), pp.
236
–
242
.10.2514/3.43933
14.
Stenning
,
A. H.
,
1980
, “
Влияние искажений на входе в осевых компрессорах
»,
ASME Trans. J. Fluids Eng.
J. Fluids Eng.
,
102
, pp.
7
–
11
.10.1115/1.3240630
15.
Greitzer
,
E. M.
, and
Strand
,
T.
,
1978
, «
Асимметричные закрученные потоки в кольцах турбомашин
»,
ASME J. Eng. Мощность
,
100
, pp.
618
–
629
.10.1115/1.3446410
16.
Vishwanath
,
K.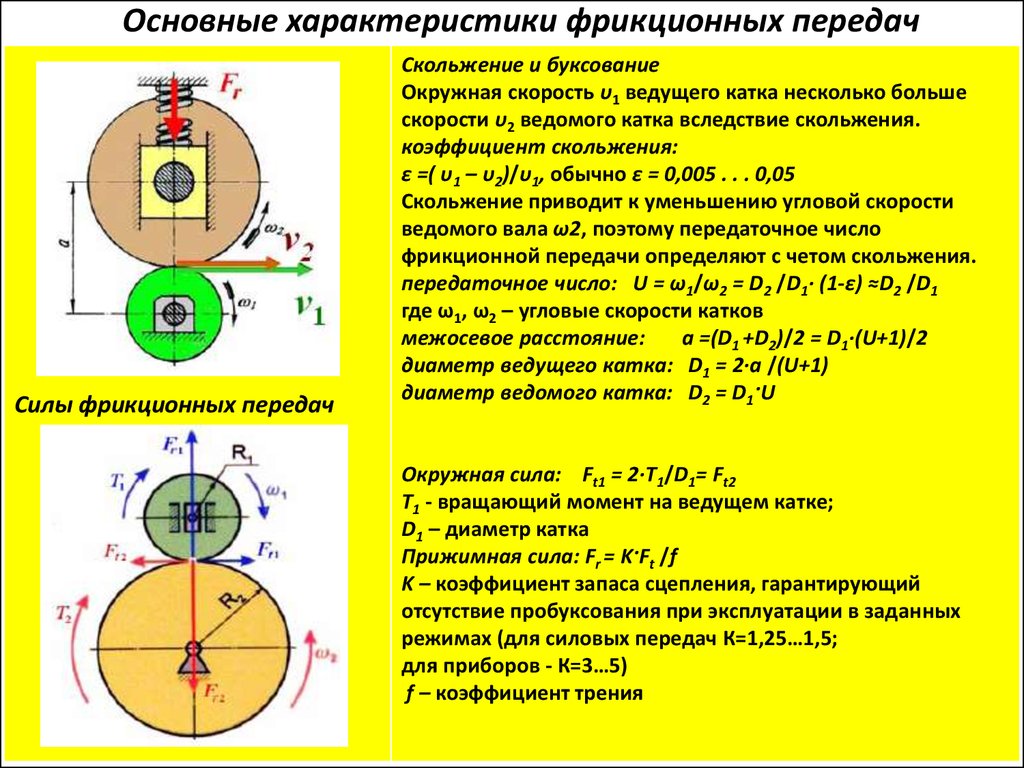
, and
Govardhan
,
M.
,
1996
, «
Влияние искривления окружности впускного отверстия и завихрения на поток жидкости ступени осевого вентилятора
»,
Proceinging ASME Turbos0003
, Бирмингем, Великобритания, 10–13 июня, документ № 96-GT-263.
17.
Govardhan
,
M.
и
Vishwanath
,
K.
,
1997
, «
9002 Инвестиции на Asceped Antaial Ascialed Ascialded Ascialed Ascialded Ascialded Ascialed Ancialeded Ancialeded Ancialeded Ancealeded Ancialeded Ancealeded Ancealedededededededededededededededed Anceial. Искажение и завихрение потока на входе
Искажение и завихрение потока на входе
”,
J. Therm. науч.
,
6
(
4
), стр.
241
–
250
.10.1007/s11630-997-0003-8
18.
Soeder
,
R. H.
, and
Bobula
,
G. A.
,
1982
, «
Влияние устойчивого искажения давления на впускное отверстие к мощности с высоким уровнем коэффициента бипаса
,”
Отчет НАСА № TM-82964
, с.
1
–
29
.
19.
Gunn
,
E. J.
,
Tooze
,
S. E.
,
Hall
,
C. A.
, and
Colin
,
Y
,
2012
, «
Экспериментальное исследование источников потерь в вентиляторе, работающем с непрерывным искажением давления торможения на входе
», Труды
ASME
Turbo Expo, Copenhagen, Denmark, June 11–15, Paper No. GT2012-68888.10.1115/GT2012-68888
20.
Hah
,
C.
,
Rabe
,
D. C.
C.
,
Sullivan
,
T. J.
, и
Wadia
,
A. R.
,
1998
, «
,
1998
,«
,
1998 9003
, «
,
98 9003
,«
,
1998 9003
, «
,
998
,«
». Ротор трансзвукового компрессора
»,
Транс. ASME J. Турбомашина. англ.
,
120
, pp.
233
–
246
.10.1115/1.2841398
21.
Hale
,
A.
, and
O’Brien
,
W.
,
1998
, “
Трехмерный код компрессора для анализа газотурбинного двигателя (TEACC) для стационарных искажений на входе
»,
Транс. ASME, J. Turbomach. англ.
,
120
, pp.
422
–
430
.10.1115/1.2841733
22.
Kaya
,
T.
,
1998
, “
Влияние искажения входного давления на вентилятор конвертируемого двигателя
”,
J.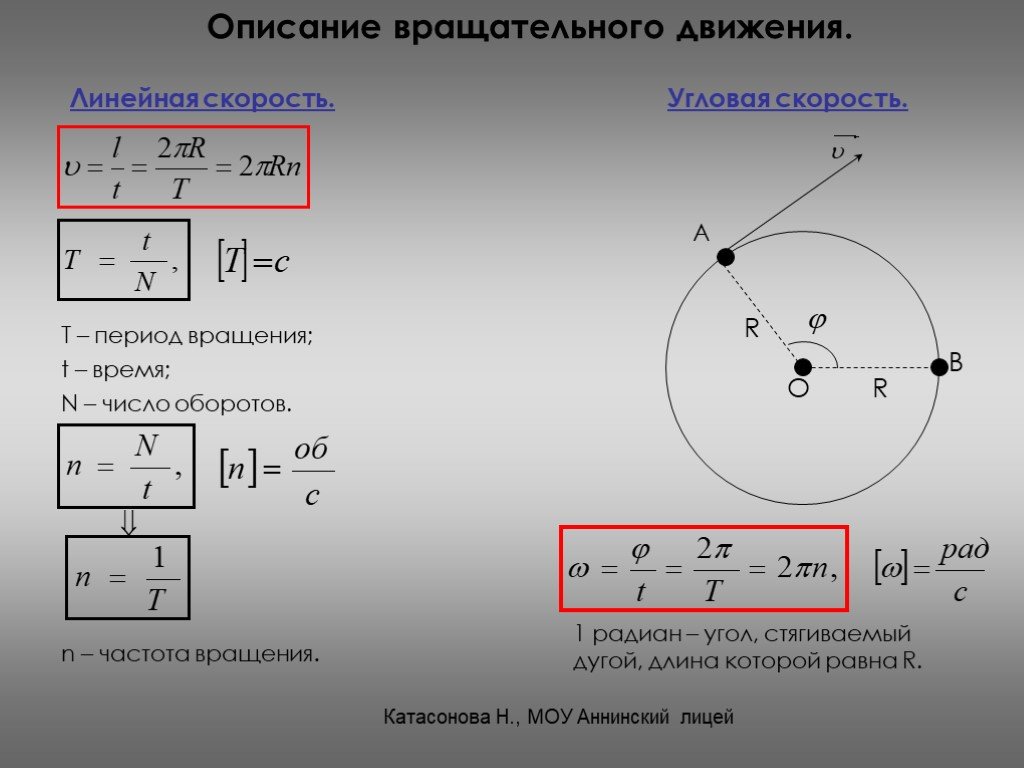 Propul. Мощность
Propul. Мощность
,
14
, стр.
82
–
89
.10.2514/2.5253
23.
Lesser
,
A.
,
Iseler
,
J.
, and
Niehuis
,
R.
,
2012
, «
Численное исследование трансзвуковой ступени осевого компрессора с искажениями на входе
»,
Материалы симуляции Nacelle Wolle и 2-го симпозиума0003
, Брауншвейг, Германия, 22–23 июня.
24.
Lesser
,
A.
,
Ciorciari
,
R.
,
Barthmes
,
S.
, and
Niehuis
,
R.
,
2012
, “
Численное исследование влияния искажений притока на трансзвуковые ступени осевого компрессора
»,
Материалы 3-го симпозиума по моделированию сваливания крыла и гондолы
, Брауншвейг, Германия, 21–22 июня.
25.
Mileshin
,
V. I.
,
Brailko
,
I. A.
,
Volkov
,
A. M.
M.
, and
Korznev
,
V. N.
,
2010
, “
Численные и экспериментальные исследования КРФ с моделированием неравномерности течения в основных условиях полета
»,
Материалы 27-го Международного конгресса авиационных наук
, Ницца, Франция, 19–24 сентября.
26.
Diaz
,
A.
,
Fernandez
,
J. M.
, and
Matigorta
,
E. B.
,
2009
, “
Калибровка цилиндрического датчика давления с тремя отверстиями для большого углового диапазона
”,
J. Изм. Инструм.
Изм. Инструм.
,
20
, pp.
57
–
68
.10.1016/j.flowmeasinst.2008.12.001
27.
SAE International
,
2002
, “
Руководство по искривлению потока на входе газотурбинного двигателя
», SAE Aerospace Report № ARP 1420, редакция B.
28.0003
, и
Breuer
,
T.
,
2010
, «
Основные принципы газ-комбинированные аспекты Turbine
,
Ancyclia of Arbine
,
Ancyclia of Arbine
,
Ancyclia of Arbine
,
Encyclia of Arbine
,
Encyclia of Arbine
,
Encyclia of Arbine. .
.
8
,
Wiley
,
Нью-Йорк
.
29.
Мистри
,
К. С.
и
Прадип
A. M.
,
2012
, «
Влияние комбинаций изменения осевого расстояния и скорости вращения ротора на производительность ступени осевого вентилятора с большим удлинением
»,
, 90c. Инст. мех. англ., Часть А
,
227
(
2
),стр.
138
–
146
.10.1177/0957650
7453
В настоящее время у вас нет доступа к этому содержимому.

 Пример, который лучше всего объясняет это, — это Земля, вращающаяся вокруг Солнца. Земля в целом совершает круговое движение вокруг Солнца.
Пример, который лучше всего объясняет это, — это Земля, вращающаяся вокруг Солнца. Земля в целом совершает круговое движение вокруг Солнца.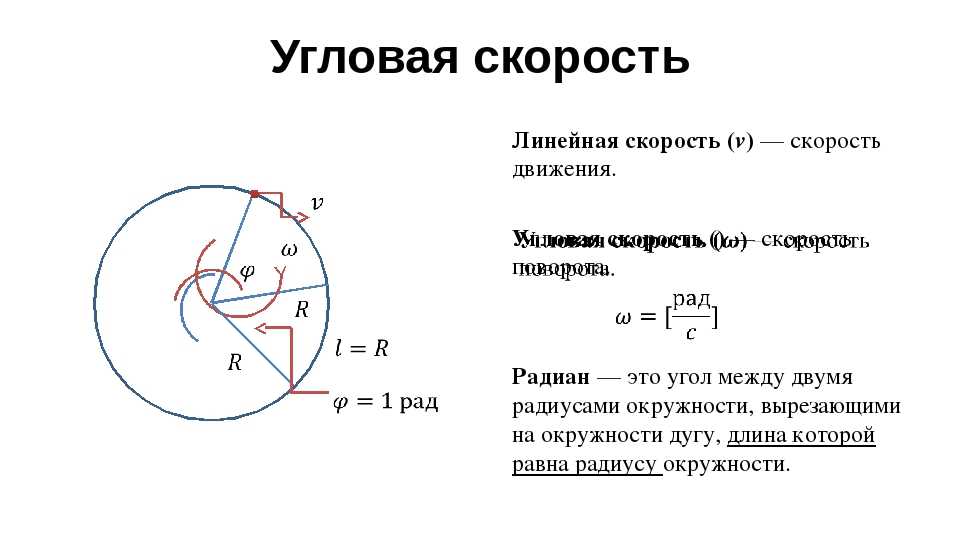

 скорость в зависимости от размера профиля, 40-50 м/с. CONTI SYNCHROFORCE CXP и Extreme — это специальные типы, которые могут работать со скоростью до 60 м/с. Для зубчатых ремней при высоких оборотах необходимо следить за уровнем шума. Профили ремня STD или CTD предназначены для самых высоких скоростей.
скорость в зависимости от размера профиля, 40-50 м/с. CONTI SYNCHROFORCE CXP и Extreme — это специальные типы, которые могут работать со скоростью до 60 м/с. Для зубчатых ремней при высоких оборотах необходимо следить за уровнем шума. Профили ремня STD или CTD предназначены для самых высоких скоростей. скорости около 20 м/с. Важно обеспечить надлежащую смазку и соблюдать все конструктивные требования производителей цепей.
скорости около 20 м/с. Важно обеспечить надлежащую смазку и соблюдать все конструктивные требования производителей цепей. Клиновые ремни с внутренними зубьями обладают большей гибкостью, требуют меньше мин. диаметр шкива и способны передавать более высокую мощность. Точно так же приводы могут обойтись меньшим количеством ремней или даже значительно меньшим диаметром шкива.
Клиновые ремни с внутренними зубьями обладают большей гибкостью, требуют меньше мин. диаметр шкива и способны передавать более высокую мощность. Точно так же приводы могут обойтись меньшим количеством ремней или даже значительно меньшим диаметром шкива.